基于時空相關性的衛星網絡流量預測

楊 力，吳 義，魏德賓，2，潘成勝

1.大連大學 信息工程學院，遼寧 大連 116622

2.南京理工大學，南京 210094

3.南京信息工程大學，南京 210044

空天地一體化網絡是通過星間鏈路和星地鏈路將地面、海上、空中和深空中的用戶、飛行器以及各種通信平臺相聯合，實現信息準確獲取、快速處理和高效傳輸的大容量信息網絡。衛星網絡作為其中的主干部分，具有全球覆蓋、接入簡單、支持多種業務、帶寬按需分配等傳統地面網絡無法比擬的優勢，在全球通信、導航定位、環境與災害監測和軍事應用等領域發揮著越來越重要的作用。

流量規劃是通信網絡設計中對流量進行科學分配的方法，經過優化的流量分配方法可以提升網絡的利用率，這對于帶寬資源受限的衛星網絡來說尤為重要[1]。流量預測是流量規劃的前提和重要基礎，在衛星網絡中，通過對各衛星下一時段的流量需求進行預測，可以提前規劃流量傳輸，計算路由表，從而主動地避免擁塞，提高傳輸效率。近幾年來，基于網絡流量預測的方法層出不窮，預測算法在預測精度和效率以及算法復雜度等方面各有優劣。但是由于衛星網絡流量呈現時空相關性的特點，傳統的流量預測方法未能達到較高的預測精度和運行效率，因此，為了解決這個問題，就必須快速、準確地對未來短時甚至長時的衛星網絡流量進行預測[2-6]。同時，衛星網絡中的節點在運動時，不同節點會具有相同或者相似的地面軌跡，而且，受人類工作、生活作息規律的影響，全球用戶流量又表現出相似的周期特點，所以，當這兩方面因素同時影響時，不同衛星流量負載之間就會出現相關性，再加上衛星網絡流量的自相似特性[7]和拓撲時變等影響著流量的預測精度，因此，在進行衛星網絡流量預測時，不僅要考慮此顆衛星的歷史流量，也應考慮與其相關的衛星流量，要兼顧預測精度和算法復雜度，達到二者的均衡。

目前，地面網絡流量的預測模型已經廣泛應用，比如時間序列分析、非線性分析、人工智能等。其中基于人工智能的方法由于簡單、魯棒性強，應用于很多的工程中[8]。例如，支持向量機[9]已經在實際地面網絡的流量預測中應用，其預測結果能較好地用于流量分配的策略中，但是，衛星網絡相比較地面，其可用資源有限和拓撲時變，這令傳統地面網絡流量預測算法[10]若是直接應用于衛星網絡，將不可避免地面臨預測精度和運行效率的挑戰。以神經網絡為基礎的組合模型以其強大的容錯性、快速并行的計算和強大的學習能力，在預測方面取得不錯的效果，但是在參數選擇上只能依靠經驗，而且算法時間復雜度高、訓練時間長以及收斂速度慢。為此，本文提出了基于奇異矩陣分解的梯度提升回歸樹方法。首先通過相關系數來確定衛星網絡流量的時空相關性，找到時空相關流量[11-13]，然后通過對時空相關流量的降維處理，減少存儲空間，降低計算時間，最后采用梯度提升回歸樹進行訓練進行平滑參數，通過測試得到相對精準的預測值。在對實際網絡流量預測的仿真試驗中，相比較傳統算法，所提的算法在性能上達到了訓練速度快的優點，同時也保證了相對精準的預測精度，較好地滿足了衛星網絡流量的預測要求，為衛星網絡的流量規劃提供了強有力的決策支持[5]。

1 衛星網絡的時空相關流量提取

在統計學中，時滯Pearson 相關方程[14]可以用來判斷兩個時間序列在一定時延下的相關程度。由于這個特點，時滯Pearson 相關方程也能夠用來有效地分析衛星網絡流量的時空相關性，假設第i號衛星流量的負載是由一系列離散觀察值組成的，也就是可以用時間序列表示為：

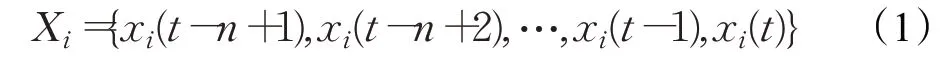
其中xi(t)是i號衛星當前最新的流量觀察值。則兩個流量時間序列Xi和Xj在時延為d下的時滯Pearson相關方程定義為：

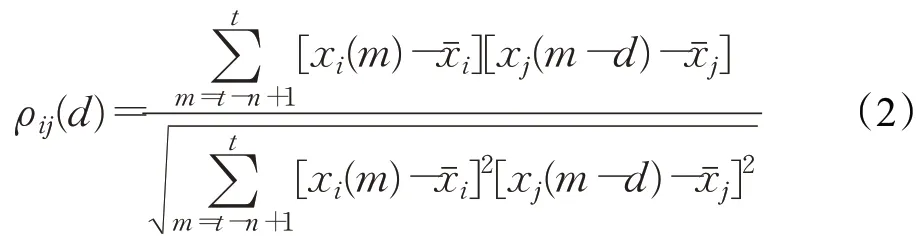
ρij(d)為Xj提前于Xi在d時間下的Pearson 相關系數，它指第i號衛星的當前流量值與第j號衛星歷史流量值之間的關聯程度。n是用于比較的流量時間序列長度，和是Xi和Xj的均值。當ρij(d)越接近+1 或者?1 時，兩個流量時間序列存在較大的時空相關性；當ρij(d)接近于0時，兩個時間序列不存在時空相關性。當i=j，d≠0，時滯Pearson 相關系數也可以反映流量時間序列在不同時滯條件下的自相關程度；當i≠j，d=0 時，時滯相關系數也可以表示兩實時流量時間序列的相關程度。對于時間相關系數，需要設置一個相應的閾值，當一個待考查流量與目標流量之間的時間相關系數的絕對值大于閾值時，可認為它是目標流量的時空相關流量，反之，則不是目標流量的時空相關流量。以時空相關流量作為預測輸入就避免了挑選輸入變量時的主觀性和盲目性。同時，以時空相關流量作為預測輸入也可以更加準確地描述待測流量的變化規律、消除不必要的干擾并最終提升訓練速度以及預測精度。

2 基于奇異矩陣分解的相關流量維度縮減與特征提取

在對網絡流量預測的過程中，由于輸入向量的維數過高，再加上輸入向量之間相互聯系，導致輸入向量之間在一定程度上存在著信息冗余，尤其是需要考慮的相關流量數量較多時，即維度較高時，這種重疊和冗余很可能會抹殺掉流量的真實特性和變化規律。此外，太多的相關數據也會占用很大的存儲容量，增加信息處理的復雜度和時間成本，所以，當挑選出的相關預測輸入流量數量較多時，必須要進行壓縮，提取相關流量間的最主要的變化特征。這里利用奇異矩陣分解法來進行降維，從多個變量中選取較少的重要變量，達到簡化數據集的目的。通過時空相關性的分析，利用時空相關流量提取過程找到m個時空相關流量，即離散的流量時間序列，X1,X2,…,Xm，每個相關流量都由n個觀察樣本值構成，Xi=[x1i,x2i,…,xni]，通常X1,X2,…,Xm在時間上是不對齊的。因此，由X1,X2,…,Xm可以構成原始預測輸入流量矩陣X(Xm×n)：

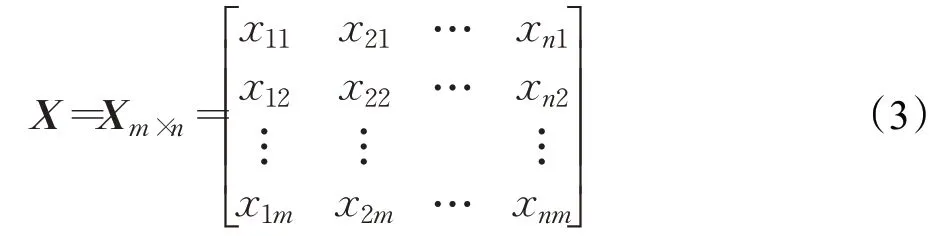
X是一個m×n的矩陣，雖然X不是方陣，但是m階XXT和n階的XXT卻是對稱矩陣，若XXT=UΛ1UT，XTX=VΛ2VT，則矩陣X的奇異值分解為：X=UΣVT，其中U是一個m×m的矩陣，U=(u1,u2,…,um) ，列向量u1,u2,…,um是XXT的特征向量，即矩陣X的左奇異矩陣，Σ是一個m×n的矩陣，V是一個n×n的矩陣，V=(v1,v2,…,vn)，列向量v1,v2,…,vn是XTX的特征向量，即X的右奇異向量。矩陣Λ1為m×m階，矩陣Λ2為n×n階，兩個矩陣對角線的非零元素相同，Σ為m×n階矩陣，位于對角線上的元素就是奇異值。設常數k是矩陣X的秩，則k≤(m,n)，當m≠n時，很明顯矩陣Λ1和Λ2階數不同，但是對角線上的非零元素相同，設矩陣Λ1的對角線上的非零元素為λ1,λ2,…,λk，其中，這些特征值都是非負的，設矩陣Σ對角線上的非零元素為σ1,σ2,…,σk，則，即所有的奇異值。隨后計算各個奇異值的方差貢獻率：，以及累計貢獻率：，根據累計貢獻率的實際要求（這里要求大于90%）來決定主要的信息個數k，這里的k個主要信息將囊括所有原始流量變量中的絕大部分信息。

3 基于梯度提升回歸樹的流量預測算法

為了提高衛星網絡流量預測的精度，本文提出一種基于梯度提升回歸樹的網絡流量預測模型。每個基本模型是一棵回歸樹，目的是用來糾正上一次迭代過程中產生的殘差。殘差就是預測值和觀測值之間的差值，差值越小說明模型的預測性能越好。為了提高模型的性能并且降低殘差值，現從損失函數入手進行改進，通過引入lg-cosh 損失函數，來降低殘差損失。lg-cosh 損失函數是一種使用魯棒性回歸的損失函數，lg-cosh損失函數表述為：。通過上述奇異矩陣分解（SVD）提取衛星網絡的時空相關流量，收集到的流量表現出時間上的特性和空間上的特性，對所確定區域內的衛星網絡流量選取與目標衛星網絡流量相關系數大的作為自變量，目標衛星網絡流量作為因變量，建立梯度提升回歸樹的預測模型，將時空相關流量作為模型的輸入變量。

已知訓練數據集為：

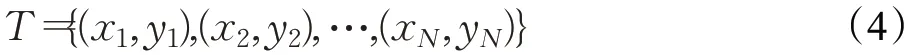
假設每棵回歸樹的葉子是J，樹的深度max_depth，這里使用的是lightGBM 中的leaf_wise 算法，而并非是level_wise，相對于level_wise 而言，leaf_wise 每次選取的都是當前損失下降最多的葉節點進行分割使得整體模型的損失下降得更多，但是當數據量較小的時候容易過擬合，因此max_depth 很好地解決了這個問題，將輸入空間劃分為J個互不相交的區域R1,R2,…,RJ，并且在每個區域上確定輸出的常量cj，則回歸樹可表述為：

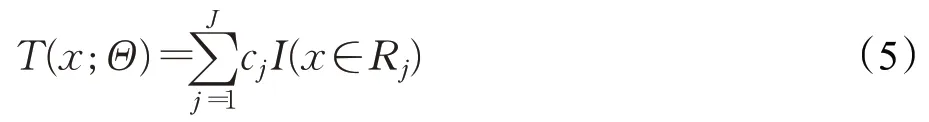
其中，Θ={(R1,c1),(R2,c2),…,(RJ,cJ)} ，表示樹的區域劃分和各區域上的常數。J是回歸樹的復雜度即葉子結點個數。首先初始化模型：

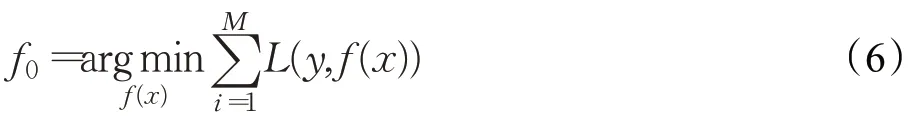
模型沿梯度下降的方向進行迭代生成M棵回歸樹，m表示第m棵樹，同時，迭代的目的是降低殘差值。對于模型的第m次迭代，在模型中計算損失函數負梯度的當前值，并將它作為殘差值的估計值rmi：

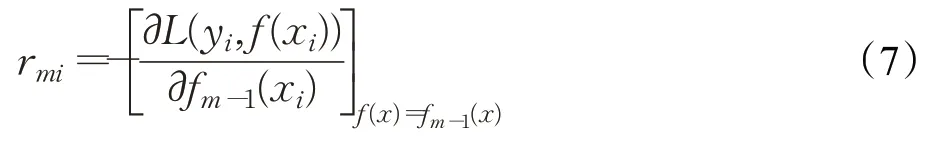
在原來梯度值的基礎上增加了對梯度值進行動量加速和減速，沿著負梯度方向一致的地方進行加速，在梯度方向不斷改變地方進行減速，更新公式為：rmi=ρrmi，其中ρ是一個動量因子，取值為ρ∈[0,1]，它的大小決定這動量項作用的強弱，當ρ=0 時沒有影響，當ρ=1時影響最強，平滑效果明顯。對于殘差，梯度提升回歸樹模型將為其擬合一個回歸樹T(x;Θ)，得到第m棵樹的葉節點區域Rmj,j=1,2,…,J，計算梯度下降的步長：

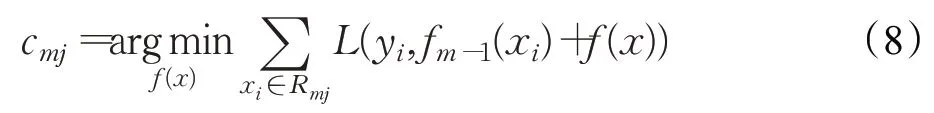
隨后更新模型：

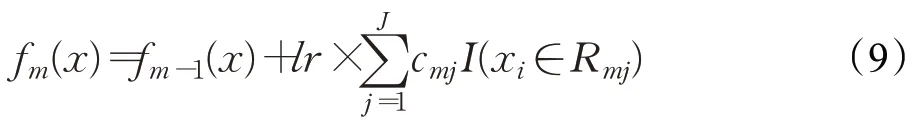
其中lr表示學習率，引入較高的學習率，是為了讓模型收斂速度加快，減少訓練時間。最后得到回歸樹：

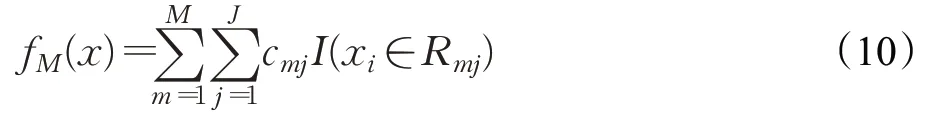
基于梯度提升回歸樹的衛星網絡流量預測模型如圖1 所示，利用訓練數據建立穩定模型，并利用測試數據對模型的性能進行評價。

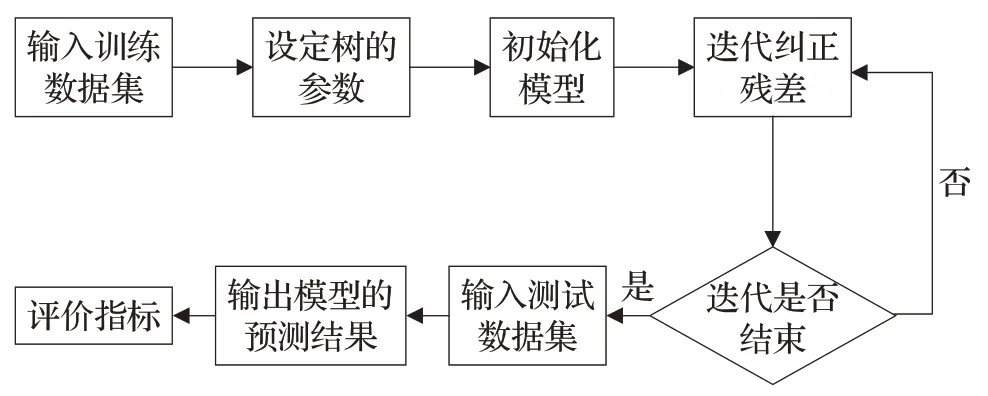
圖1 基于梯度提升回歸樹的衛星網絡流量建模流程圖

梯度提升回歸樹沿梯度下降的方向構建一個新的模型，這里利用提高學習率從而優化算法收斂的方法，此外，通過最小化損失函數的期望值來不斷更新模型，從而使得模型趨于穩定，最后用測試數據預測未來值進行驗證。該模型在訓練過程中不僅引入了lg-cosh損失函數作為擬合殘差的方法，還考慮模型的預測結果受到衛星網絡流量的時空相關性因素的影響，同時通過不斷調整基本模型的權重來提高預測精度。

4 仿真與結果分析

4.1 時空相關分析

在本實驗中，首先利用STK 搭建一個銥星星座，如圖2所示。

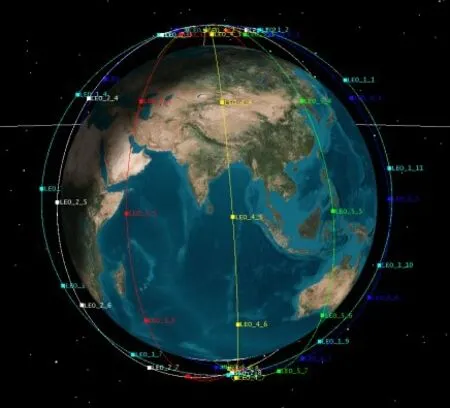
圖2 銥星星座

在t時刻，選取LEO_4_5 衛星作為待預測衛星，設為1 號衛星，此時1 號衛星的流量為X1(t)，通過觀察1號衛星在這段時間內的流量時間序列，它的流量負載在白天的時候相對較高，在接近午夜和凌晨的時較低，這也就表明了衛星網絡流量具有周期性變化。因為在銥星星座中，衛星繞自身軌道運轉的周期約為110 min，地球自轉周期約為1 440 min，流量的變化周期是24 h，所以衛星接收到的總流量會按照三者的最小公倍數，約為24 h，周期性的變化。將所選取的9 顆銥星衛星所覆蓋的區域作為研究區域，在該區域當中，若有衛星與1 號衛星星下點的連線和1 號衛星與其星下點連線的夾角小于或者等于α，其中α取60，那么收集該衛星在一定時間段內的衛星網絡流量，作為衛星網絡流量時空相關性分析的條件。根據計算，共有8顆衛星在此時間段內與1號衛星星下點的連線夾角小于或者等于α，所以取此8 顆衛星收集的流量進行時空相關性分析，此8 顆衛星分別為LEO_3_4、LEO_3_5、LEO_3_6、LEO_4_4、LEO_4_6、LEO_5_4、LEO_5_5、LEO_5_6。

如圖3所示，1號衛星和與2號衛星與地心的夾角為θ，即地心角，且h1、h2分別表示1號衛星與其星下點的距離，2號衛星與1號衛星星下點的距離，α為h1與h2之間的夾角，d為1 號衛星與2 號衛星的星間鏈路距離，Re為地球半徑。由于所選衛星是處于同一軌道高度，所以星間鏈路長度d，可表示為所以h1與h2之間夾角為。首先收集1號衛星在400 min內的流量時間序列，每隔60 min進行一次測量。

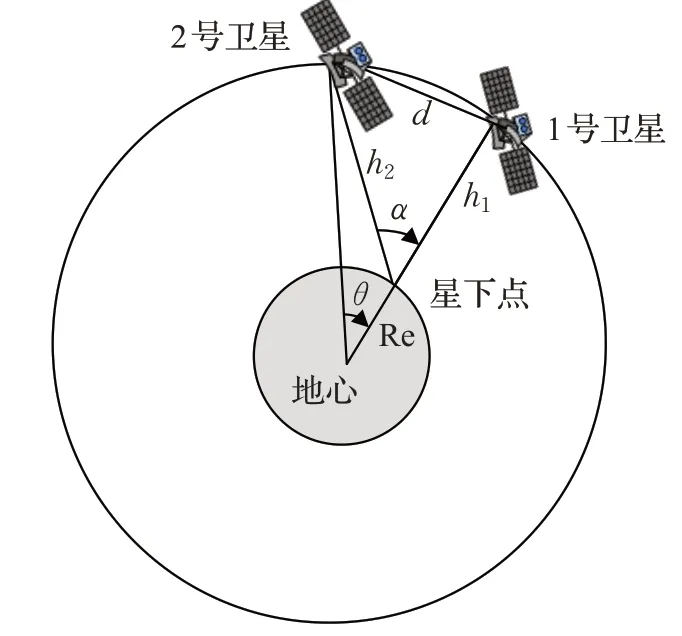
圖3 兩顆衛星在1號衛星星下點處的夾角

在獲得所有衛星在400 min 內的流量時間序列后，作為預測模型的輸入變量，然后利用Pearson 方程來計算1 號衛星與其他各衛星流量在不同時滯條件下的相關系數，將結果由小到大進行排列，選取了前32個相關程度較高的時空相關流量列于表中。設置的相關系數的閾值為0.75，此時獲得了較低的MAE結果，當時空相關系數閾值小于0.75 時，過多的低相關流量被選出，因此導致預測過程受到了較大的干擾，預測的MAE 結果偏高。當時空相關系數閾值設置大于0.75時，挑選出的少量時空相關流量不足以涵蓋目標流量的全部特性，因此MAE 結果同樣偏高。而0.75 的閾值正好在兩種之中，所以獲得較好的預測結果。這樣，通過分析與驗證，使得復雜度降低了，精度也有所提高。

設衛星序列號為K，與目標衛星的相關系數設為P。第1號衛星與各衛星流量之間的時滯Pearson相關系數如表1所示。

如表1所示，第1號衛星與這32組衛星流量都具有較高的時空相關性（相關系數都大于0.75），但是其中有16組的時空相關系數在0.8以上，此處的0.8閾值經分析之后相較于0.75預測更加準確，所以選取0.8作為依據，以16 組為待測的第1 號衛星的時空相關流量。時空相關流量體現了衛星網絡流量間的互相關性與自相關性。以時空相關流量作為預測可排除其他無關流量的干擾提升最終結果的準確度。然而由于挑選出的相關流量數目較多且相互間存在大量的信息重疊和冗余。因此，使用SVD 對這16 組相關流量進行降維，將這16組相關流量的分析結果列表于表2。

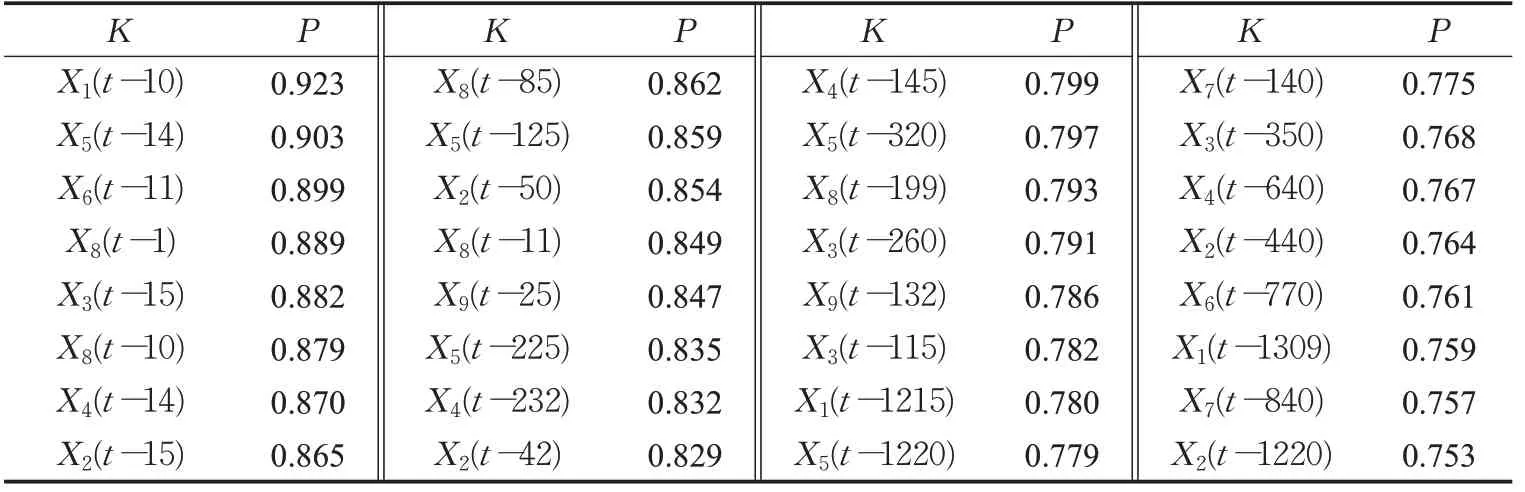
表1 第1號衛星與各衛星流量之間的時滯Pearson相關系數（相關系數閾值為0.75）

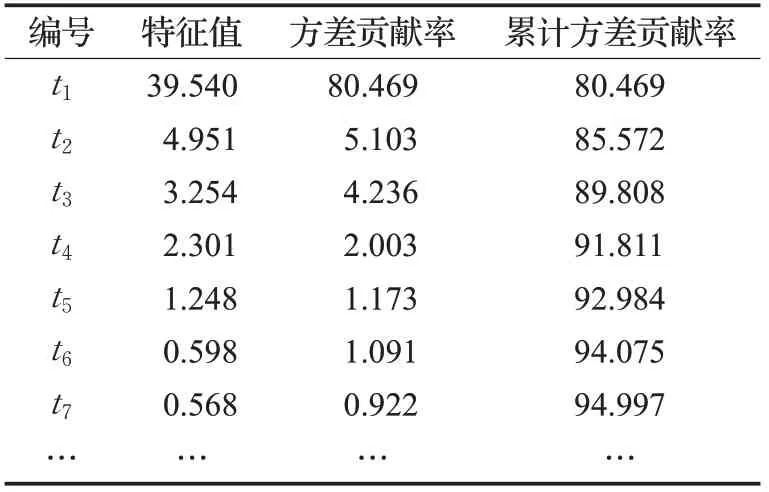
表2 16組相關流量的分析結果

如表2 所示，前4 個主要的信息t1,t2,t3,t4，已經保留了原始16組的相關變量中91.811%的方差和信息，所以，將這4 個主要信息作為新的不相關變量，來替代原始的16組相關變量充當預測算法的最終輸入。在收集的實驗數據中，選取前300 組的數據作為訓練樣本，最后100 組的數據將作為測試樣本。收集到的原始衛星網絡流量如圖4所示。

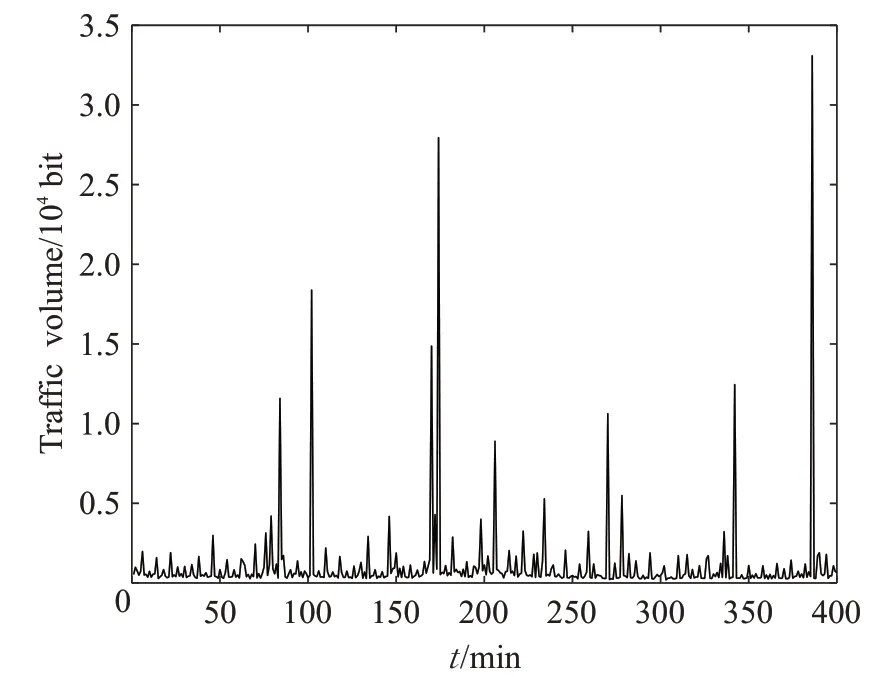
圖4 原始衛星網絡流量

4.2 性能評價指標

實驗采用預測誤差百分比絕對值均值（MAPE）、預測誤差絕對值均值（MAE）來評估模型的預測性能，其值越小表示預測結果越準確。，其中y(i)代表流量的實際值，y"(i)代表流量的預測值，m是測試樣本的數量。

4.3 仿真校驗

考慮到其中消除冗余和重疊信息的同時，可能會出現將某些重要的信息也會一并消除，所以通過圖5、圖6的仿真對比發現，S-GBDT模型的預測精度比GBDT預測模型的精度平均高47%，而且其訓練時間較GBDT訓練的時間大幅度縮短，整體上提高了39%，如表3所示。

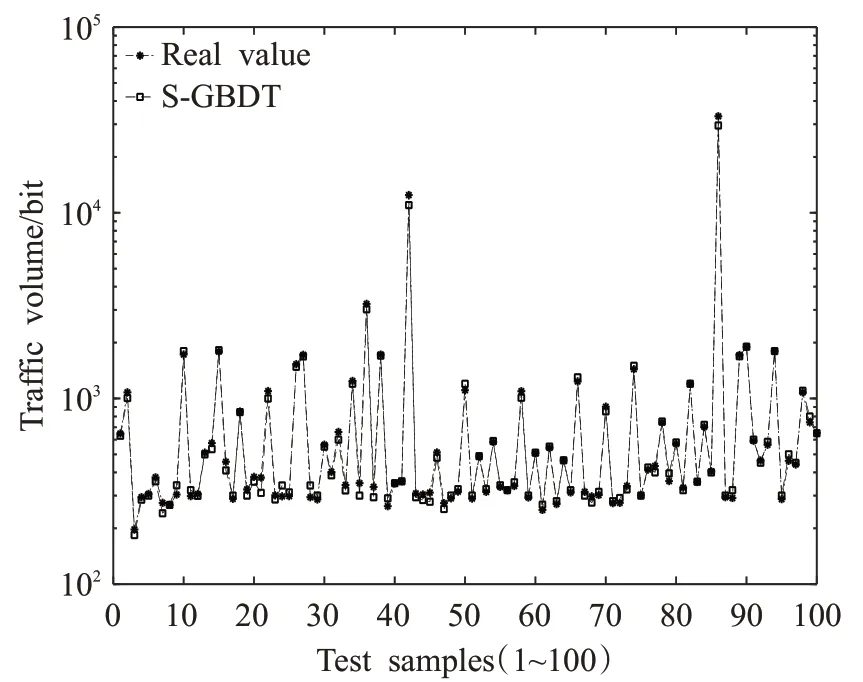
圖5 S-GBDT算法預測結果

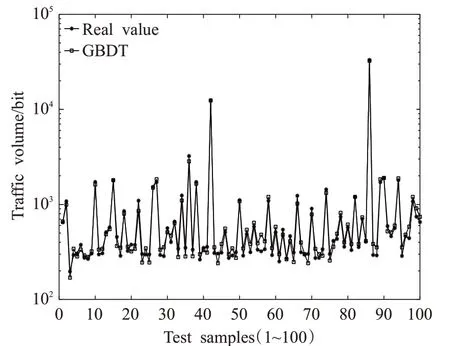
圖6 GBDT算法預測結果

表3 各算法的預測性能

最后將兩種方法進行誤差對比，S-GBDT模型的誤差相較于GBDT 模型的誤差就比較低。兩種方法的誤差對比圖如圖7所示。

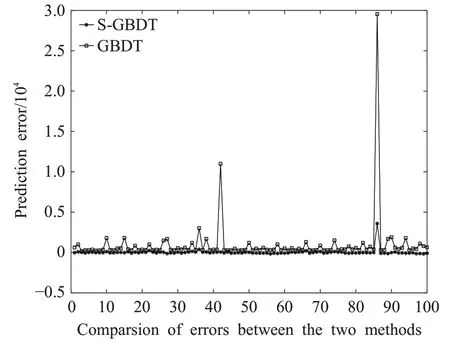
圖7 兩種方法誤差對比圖

5 結束語

本文利用收集到的衛星網絡流量時間序列，提出了基于奇異矩陣分解的梯度提升決策樹的模型來預測衛星網絡流量。通過在決策樹的訓練過程中不斷對弱學習器的權重進行優化，使其成為強學習器，從而提高了模型的預測精度。大量的仿真實驗證明，相比較其他的預測算法，S-GBDT算法擁有相對較高的預測準確度以及更少的計算和訓練時間。所以，該算法對于實際的衛星網絡系統應具有巨大的應用價值。目前，對衛星網絡流量預測的研究越來越深入，下一步工作將嘗試將流量預測值與擁塞控制相結合。