基于鄰域圖的低秩投影學習

胡文濤，陳秀宏

江南大學 數字媒體學院，江蘇 無錫 214122

特征提取在模式識別和計算機視覺等領域發揮著重要作用[1-3]。經典的特征提取算法有主成分分析（Principal Component Analysis，PCA）[4]、局部保持投影（Locality Preserving Projections，LPP）[5]、鄰域保持嵌入（Neighborhood Preserving Embedding，NPE）[6]和稀疏保持投影（Sparsity Preserving Projections，SPP）[7]等，其中PCA是尋找最大方差的投影方向，使得降維之后的低維表示可以保留數據的主要信息，而LPP、NPE 和SPP 都是旨在保留數據降維之后的局部結構。這些方法也可以看作是基于圖的特征提取算法[8]。

近年來，低秩表示（Low-Rank Representation，LRR）[9]因其對含噪數據的魯棒性且能保持數據的整體結構而受到了廣泛的關注。Liu 等[10]提出的隱式低秩表示（Latent Low-Rank Representation，LatLRR），通過從矩陣的縱向和橫向處理信息，恢復出有效的主要信息和隱藏的顯著信息，并取得了較好的實驗效果。但是，LatLRR 并沒有把兩個低秩矩陣聯合學習，得到的結果不是全局最優解。為了解決這個問題，Yin 等[11]提出了雙低秩表示算法（Double Low-Rank Representation，DLRR），該算法通過聯合學習行低秩矩陣和列低秩矩陣來同時恢復數據的主要信息和顯著信息。然而，上述的無監督特征提取方法只考慮了數據的局部或全局幾何關系。例如，NPE、LPP和SPP只利用最近鄰樣本的局部幾何關系，而基于LRR 的特征提取方法只保留了數據的全局結構。一般地，全局結構和局部結構都反映了數據之間的關系，對于不同的數據集，僅僅保留一種結構往往無法獲得良好的性能。Wen 等[12]提出的基于圖正則重構的低秩投影學習算法（Low-Rank Preserving Projection via Graph Regularized Reconstruction，LRPP_GRR），通過在重構項上施加圖約束來保持局部結構，但算法沒考慮數據樣本本身含有的噪聲。Fang等[13]提出的增強近似低秩投影學習算法（Enhanced Approximate Low-rank Projection Learning，EALPL），使用重構矩陣和投影矩陣近似表示LatLRR 算法中的低秩投影矩陣，從而在提取判別特征的同時有效地降維，但算法沒有考慮數據在重構過程中的殘差，導致存在冗余特征，影響識別精度。文獻[14]提出的低秩線性嵌入算法（Low-Rank Linear Embedding，LRLE）通過在線性判別子空間構造回歸模型，并在模型中用兩個矩陣近似地表示低秩系數矩陣，從而提取更多的判別特征，取得了不錯的效果。最后，上述特征提取方法不具有很好的可解釋性，因為提取的特征是所有原始特征的簡單線性組合，如PCA、LPP、SPP 等，這些方法提取出的特征沒有區分度，因此很難得到有鑒別性的特征；而且它們提取了許多包含離群點和噪聲的特征，這與特征提取的目的自相矛盾，因為特征提取的目的是提取有用的、有判別性的特征。

為了解決以上述問題，本文提出一種基于鄰域圖的低秩投影學習算法（Low-Rank Projection Learning based on Neighbor Graph，NGLRPL），首先在聯合低秩矩陣的重構殘差項上施加圖約束，這樣就能同時保持數據的局部結構和整體結構，從而保證算法能得到全局最優值投影矩陣；其次，在算法模型中約束數據樣本存在的噪聲，同時利用L2，1范數獲得行稀疏的投影矩陣，提高投影矩陣的可解釋性；最后，模型通過交替迭代方法求解，并在多個數據集上進行實驗，說明了算法的有效性。

1 相關工作

假設給定訓練樣本矩陣X∈Rm×n，其中，每個列向量xi(i=1,2,…,n)為一個樣本，m為樣本的維數，n為訓練樣本的個數。

1.1 基于低秩表示的特征提取

基于數據近似地從多個獨立的聯合子空間中提取的假設，LRR尋找數據集在過完備字典集上的最低秩表示，其模型如下：

式中，||Z||*是矩陣Z的核范數，即矩陣Z所有奇異值之和。系數矩陣Z中的每個元素zij表示了樣本xi和xj之間的“相似性”。針對模型（1）沒有學習用于特征提取的投影矩陣且沒有考慮樣本中含有的噪聲，Liu 等進一步提出了以下LatLRR模型：

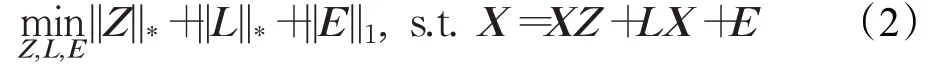
式中，E∈Rm×n是樣本中的噪聲矩陣，并對其施加了稀疏約束；L∈Rm×m是投影矩陣，能夠提取數據圖像的顯著特征。然而，LatLRR 提取的特征不能保留數據的全局結構和主要信息。為了得到更具魯棒性的投影，Yin等[11]提出了雙低秩表示模型（DLRR）：

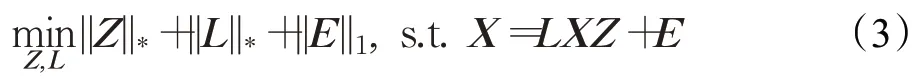
在這個算法中，學習到的投影矩陣L能夠同時保存數據的主要信息和全局結構。上述算法很好的保持了數據樣本的整體機構，但是卻忽視了數據樣本的局部結構。

1.2 基于鄰域圖的流形學習

鄰域圖可以保持數據的局部幾何結構。對于一個含n個樣本的數據矩陣X=[x1,x2,…,xn] ∈Rm×n，基于鄰域圖的流形學習方法，首先要構造一個鄰域圖W來表示樣本的局部關系，然后通過求解以下優化問題進行投影學習：

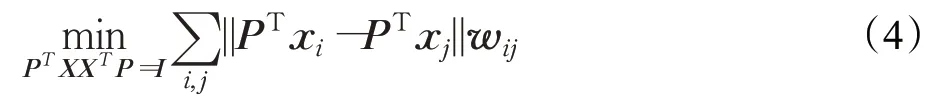
式中，P是投影矩陣；圖矩陣W中每個元素wij定義為：

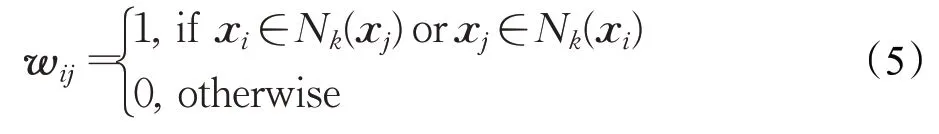
式中，Nk(xj)表示距離樣本xj最近的k個樣本的集合，wij=1 表示樣本xi是樣本xj的近鄰。

2 基于鄰域圖的低秩投影學習

DLRR算法只考慮了數據樣本的整體結構，且提取的投影矩陣只是原始特征的線性組合，沒有很好的可解釋性，而且沒有對數據樣本進行降維。為此，本文提出以下基于鄰域圖的低秩投影學習：

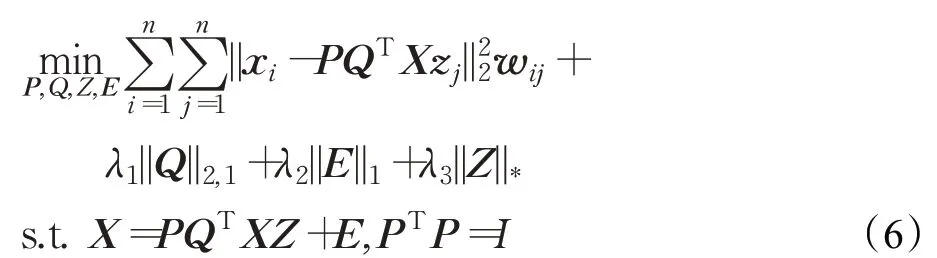
式中，Q∈Rm×d表示投影矩陣，P∈Rm×d表示重構矩陣，d(d ＜m)是降維后特征的維數。QTX是算法提取的特征子空間，其維數d是可變的。目標函數中第一項表示如果樣本xi和xj互為近鄰，那么樣本xi和重構樣本PQTXzj也應該彼此互為近鄰[12]，這樣既描述了數據樣本和重構數據之間的殘差，又考慮了數據的局部結構；第二項利用L2，1范數的行稀疏性質來剔除冗余特征，以便提取顯著特征，提高投影矩陣的可解釋性；第三項用來保證噪聲矩陣是稀疏的；第四項用來保證最終得到的系數矩陣是低秩的，從而保留數據樣本的全局結構。λ1、λ2和λ3是正則化參數。對矩陣P施加正交約束得到，避免式（6）出現平凡解。

模型（6）可使用交替方向乘子法[15]求解。首先，為了使模型（6）可分，引入兩個輔助變量Y和U：

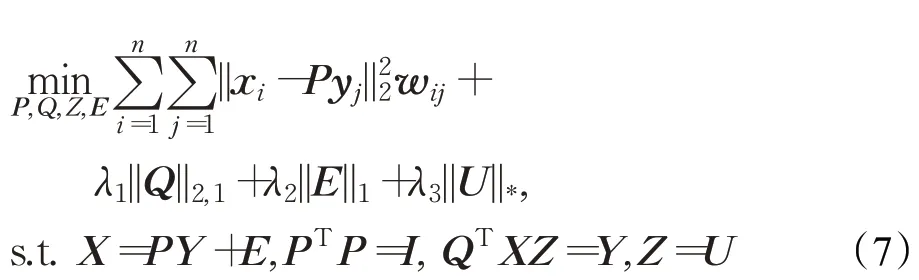
該問題的增廣Langrange函數可以定義為：

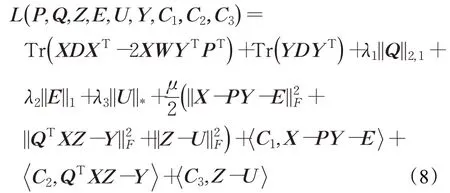
式中，D=diag(D11,D22,…,Dnn) 是一個對角矩陣，且Dii=，C1、C2、C3是Langrange乘子矩陣，μ是懲罰參數。于是，得到以下交替法求解方法。當P、Q、E、Z、U固定時求Y。公式（8）可變為：

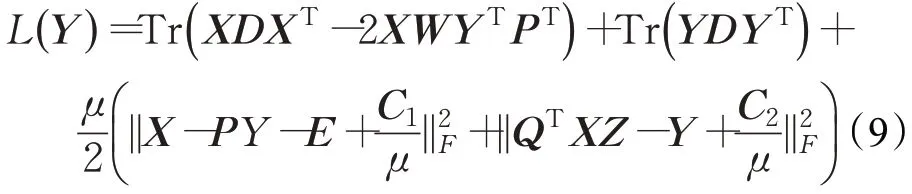
關于Y求偏導并令其結果為0可得：

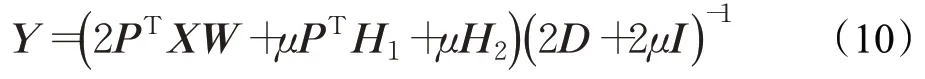
當P、Q、E、Z、Y固定而求U時可得以下問題：

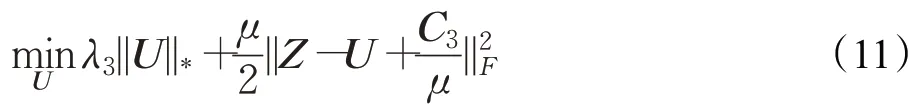
此時，可通過奇異值閾值算子（Singular Value Thresholding operator，SVT）[16]得到解U。設矩陣的奇異值分解為：

式中，B和V均為列正交的矩陣，∑=diag(σ1,σ2,…,σr)，σ1,σ2,…,σr是奇異值且均為正數，則式（10）的解為：

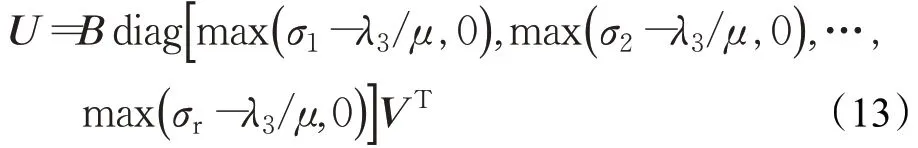
當P,Q,E,U,Y固定而求Z時，公式（8）可變為：

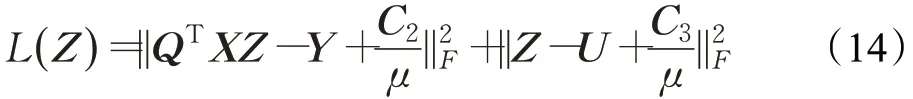
關于Z求導并令其為0可得：

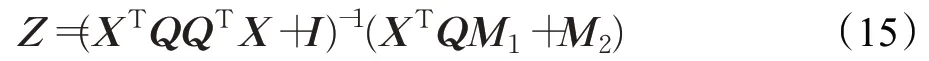
當P,U,Y,E,Z固定而求Q時，公式（8）變為：

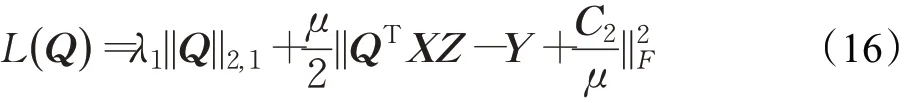
關于Q求導并令其結果為0可得：

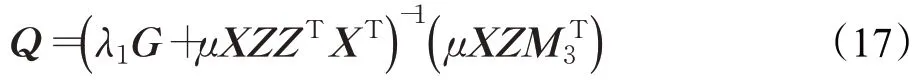
當P、U、Q、Y、Z固定而求E時，得以下問題：

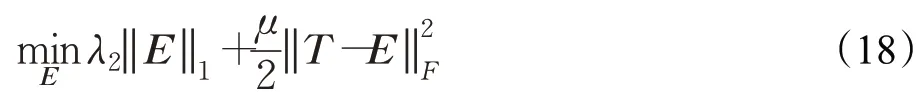
由文獻[17]可知該問題的解為：

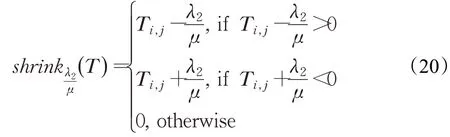
當Z、U、Q、Y、E固定而求P時，公式（8）轉化為以下問題：

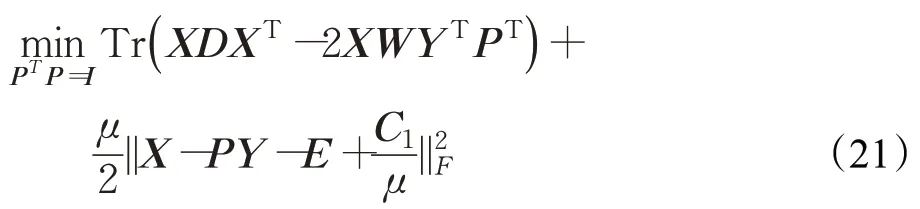
目標函數關于P求偏導并令其結果為0得：

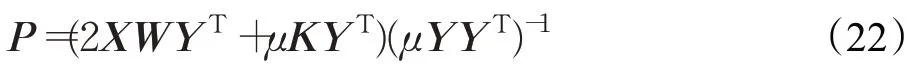
最后，Langrange乘子矩陣C1、C2、C3和懲罰參數μ的迭代規則如下：

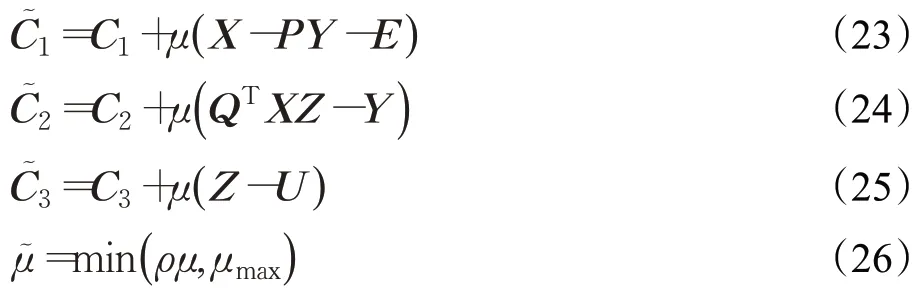
式中，ρ和μmax都是常數。為了提高算法速度，本文實驗首先通過PCA 初始化正交矩陣P，實驗判定收斂的條件為迭代中最近兩次目標函數值差值的絕對值小于0.000 1。綜上所述，本文NGLRPL算法步驟如下：

算法NGLRPL

輸入：數據集X，維數d，參數λ1、λ2和λ3

初始化：通過PCA 初始化正交矩陣P，Q=P，Z=W，U=Z，Y=QTXZ，C1=C2=C3=0，μ=0.1，ρ=1.01，μmax=105

while no convergence do

1. 通過（10）更新矩陣Y

2. 通過（13）更新矩陣U

3. 通過（15）更新矩陣Z

4. 通過（17）更新矩陣Q

5. 通過（19）更新矩陣E

6. 通過（22）更新矩陣P

7. 通過（23）、（24）、（25）、（26）更新矩陣C1、C2、C3和μ

end while；

輸出：投影矩陣Q

在算法迭代結束得到投影矩陣Q后，對測試樣本進行降維。對于降維之后的測試樣本點，選擇距離該測試樣本點距離最小的訓練樣本點標簽作為類別標簽，直至所有測試樣本點完成分類。

本文算法計算復雜度主要在矩陣求逆和矩陣SVD分解，暫不考慮矩陣乘法和加法的計算復雜度。對于m×m的矩陣，其求逆的計算復雜度為O(m3)。對于m×n的矩陣，其進行SVD 分解的復雜度為O(mn2)。在上述算法中，計算復雜度最高的是在求Y、U、Z和Q上，分別為O(n3)、O(mn2)、O(n3)和O(m3)。所以，本文算法總的復雜度是O(τ(2n3+m3+mn2))，其中τ為最大迭代次數。

3 實驗結果與分析

本文實驗的硬件環境為Windows 10，Intel Core i5 3.3 GHz CPU，內存為8 GB，編程軟件使用的是Matlab 2016a。為了驗證本文算法的性能，分別在數據集COIL20、BioID和AR數據集上進行實驗，并將結果分別與EALPL、LRPP_GRR、LRLE、LatLRR和LPP等方法進行比較。實驗中首先將數據集圖像裁剪成大小的灰度圖，然后將這些灰度圖重構為1 024維的向量，并做歸一化處理而構成實驗用的數據矩陣。所有實驗均獨立隨機運行了20次，對其平均最佳識別率進行比較。

3.1 數據集

BioID（https：//www.bioid.com/facedb/）人臉數據集包含來自23個測試人員的1 521幅灰度圖像，這些圖像分別是在不同的光照，姿態和表情變化的情況下采集的。

COIL20（http：//www.cs.columbia.edu/CAVE/software/softlib/coil-20.php）數據集包含20 個物品的1 440 個圖像，每個物品姿勢間隔5度采集了72張圖像。

AR人臉庫包含來自126人的4 000多幅人臉圖像，包含56個女性和70個男性。每一個人的人臉圖像包含了表情變化、光照變化和遮擋變化（戴墨鏡和圍巾）等干擾。實驗時隨機選取120人，每人26幅圖像。數據集部分圖像如圖1所示。

3.2 正則化參數對實驗的影響

本節進行算法的收斂性實驗和討論正則化參數λ1、λ2和λ3對識別率的影響，分別在BioID、COIL20 和AR 人臉庫這3 個數據集上進行實驗，每個類別分別選取21、20和16張作為訓練集，其余的圖像用作測試集。

如圖2 是在COIL20 和AR 人臉庫上正則參數與平均識別率的關系圖。λ2控制噪聲的稀疏度，在AR 和COIL20 數據集上取10-4，在BioID 數據集上取10?5。對正則化參數λ1和λ3取值設置在[10?6，100]。本文算法在COIL20、AR、BioID 數據集上當λ1分別取值在10?4、10?5、10?6，λ3分別取值在100、100、1時，識別效果達到最佳狀態。當識別率達到最高時，λ3數值比較大，說明在這3 個數據集上保持整體結構的低秩矩陣對本文算法性能起比較大的作用。

3.3 特征維數對實驗的影響

為了驗證特征維數對于實驗的影響，本節通過比較在不同維度下算法的識別效率來驗證特征維數對實驗的影響。在AR、COIL20 和BioID 數據集上分別選取16、20、21個圖像作為訓練樣本。

圖1 數據集的部分圖像

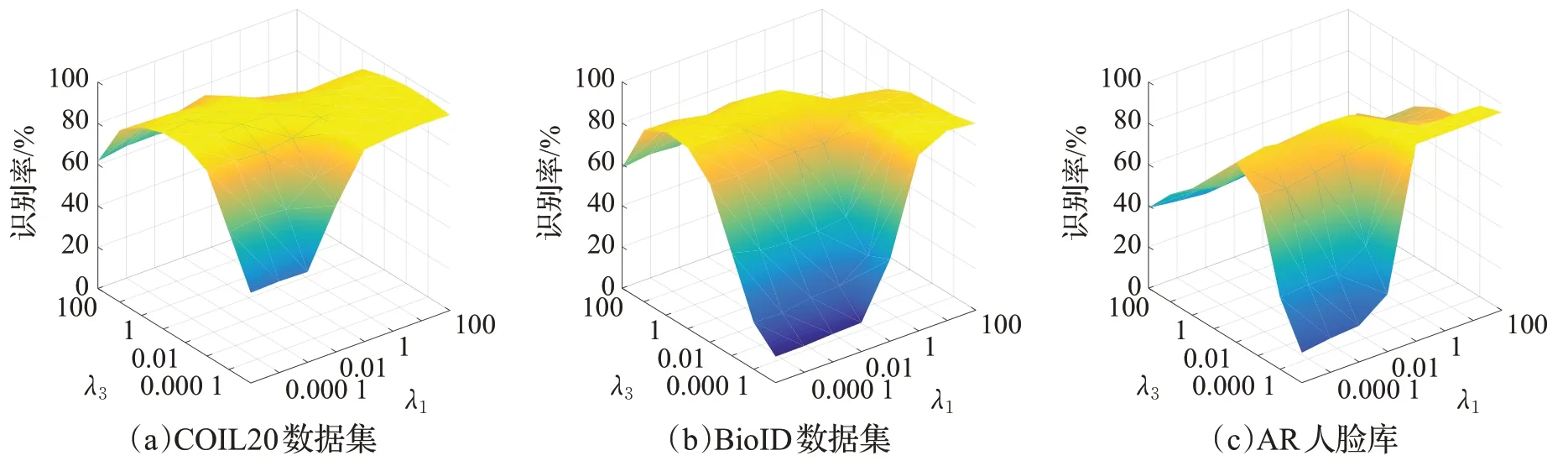
圖2 正則化參數與平均識別率的關系圖

圖3 特征維數與平均識別率的關系圖

如圖3 是在各數據集上特征維數與平均識別率的關系圖（由于LatLRR并未對數據降維，故圖3并未列出LatLRR的曲線，每個數據集都是從10維開始），本文算法在低維時識別率較其他算法偏低，但是從80 維左右開始是所有算法中最高的，這是由于在低維時許多具有判別性的特征沒有提取出來，導致識別率偏低。當維度升高時，由于L2，1具有行稀疏的性質，可以剔除許多不具有判別性的特征和噪聲。同時，由于存在對系數矩陣的低秩約束，可以很好地剔除離散點的干擾。從圖3還可以看出LPP 算法對于維數比較敏感，而本文算法從100維開始的識別率相對穩定。

3.4 訓練樣本數對識別精度的影響

本節討論了在各數據集上訓練樣本數對識別精度的影響。在AR 和BioID 數據集上維數設置為200，在COIL20數據集上維數設置為180。表1至表3給出了本文算法和對比算法在不同訓練樣本數下的識別精度。

在不同訓練樣本數目下，NGLRPL算法均優于其他5種算法且隨著訓練樣本數的增加識別率也相應增加。NGLRPL 算法識別率比LRPP_GRR 高是因為LRPP_GRR 算法并未考慮到數據的樣本本身存在的噪聲的影響（如AR數據集中墨鏡和圍巾），使得在學習投影過程中不能較好地提取具有判別性的特征。EALPL算法的識別率比NGLRPL算法低，是由于其并未考慮算法在投影和重構過程中產生的殘差，約束殘差可使得在學習投影的過程中剔除冗余特征。NGLRPL 算法比LatLRR、LPP 和LRLE 算法的識別率高，是因為LatLRR算法和LPP 算法只單獨考慮了數據的整體結構或者局部結構而NGLRPL算法同時考慮兩種結構，從而減小離散值的影響。同時，LRLE 算法盡管同時考慮了整體結構和局部結構，但是其并未對投影矩陣進行稀疏約束導致其不能有效提取出顯著的特征。

表4 列出了各算法在COIL20 和BioID 上用不同訓練樣本數所消耗的時間，除LPP 算法用時明顯較少，本文算法在大部分情況下計算時間小于其他4種算法，這得益于本文算法具有較好的收斂性，在數次迭代之后能快速收斂。

表1 AR人臉庫上各算法的平均識別率 %

表2 COIL20數據集上各算法的平均識別率%

表3 BioID人臉庫上各算法的平均識別率 %

表4 COIL20數據集和BioID人臉庫上算法所消耗的時間 s

4 結論

本文提出了一種基于鄰域圖的低秩投影無監督學習算法，通過把鄰域圖和聯合低秩系數矩陣的數據重構殘差相結合使算法在學習投影的過程中同時保持數據的局部結構和整體結構。同時，對投影矩陣施加L2，1范數正則化的稀疏約束，以便能提取更具有判別性的特征。在多個數據集上的實驗表明，本文算法取得了比其他算法更好的識別精度。本文提出的算法復雜度相對較高，在實際應用中如何降低復雜度值得進一步研究。