基于問題導向的單元復習課深度學習教學設計
——以《解三角形》為例
廣東省汕頭市澄海中學 (515800) 陳煥濤廣東省佛山市順德區容山中學 (528303) 潘敬貞云南師范大學信息學院 (650500) 唐明超
1.引言
單元復習課教學是高中數學的重要課型之一,完成某個單元的新課教學后我們都需要對本單元進行復習.單元復習教師的做法更多是回顧復習(本單元的概念、定理以及公式)、例題示范、試題訓練的基本模式,不同教師雖然選取的例題與練習題有所不同,但教學活動大同小異.這種復習方式不僅耗時較長,而且問題意識不突出,知識碎片化依然存在,學生很難構建知識體系,也很難做到觸類旁通,解題能力也難以得到有效提高.單元復習的核心目標是幫助學生梳理并整合基礎知識,構建知識體系,最終提升解題能力,發展數學素養,以問題為導向的單元復習課教學卻能很好的達成以上教學目標,實現深度學習.文章主要呈現用例題引導學生復習解三角形的基本概念、基本定理以及基本公式,用變式引領構建知識體系,用變式訓練提升解題能力并發展數學核心素養,用一題多解拓寬解題思路培育創新意識的整個過程,試圖建構一種指向深度學習的單元復習課教學模式,重點回答應該怎么做以及為什么這樣做兩個核心問題.
2.教學案例
2.1 用例題引領鞏固雙基
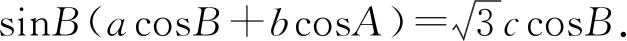

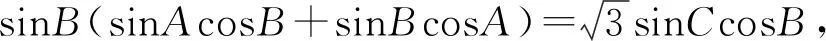
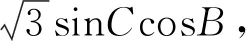
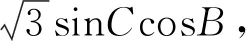
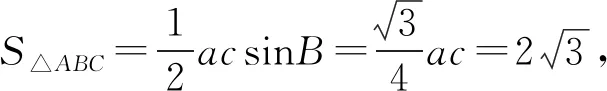
評注:例1屬于基礎問題,絕大部分學生都能快速解答,增強進一步探究學習的熱情,容易調動學習積極性,提高學生參與度.符合由淺入深,由易到難的層級遞進的探究與學習規律,能為進一步展開教學活動奠定良好基礎.
設計意圖:由于例題的解答用到了正弦定理、余弦定理、三角形面積公式、三角形內角和定理等知識,可以在解題時借機引導學生回顧復習相關知識點,可以達到回顧復習、梳理整合知識的目的,在反思小結階段適當提煉升華可以有效深化難點并突出重點的作用.歸納基于問題背景以及轉化與化歸、方程等思想,經過運算、代換、推理,求解三角形未知的邊、角及三角形有關問題的求解策略,積累解題經驗,提升能力并培育核心素養.
2.2 基于問題變式構建知識體系


變式2 (串聯同角三角函數基本關系)△ABC的內角A,B,C所對的邊分別為a,b,c,已知2sinBtanB=3,求角B.

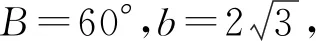



設計意圖:基于以上4個變式問題可以有效達成復習降冪公式、同角三角函數基本關系、重要不等式、三角函數的性質等基礎知識;進一步鞏固了正弦定理、余弦定理、三角形面積公式以及內角和定理等知識,將各個知識點有效串聯起來,構建知識體系,使知識網絡化.同時進一步提升學生的代數變形能力,解決問題的能力等.
2.3 基于問題變式發展素養
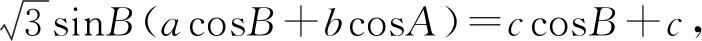

變式6△ABC的內角A,B,C所對的邊分別為a,b,c,若B=60°,△ABC外接圓的面積為4π,求△ABC周長的最大值.
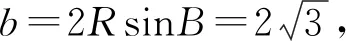

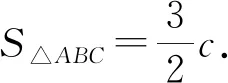
變式8△ABC的內角A,B,C所對的邊分別為a,b,c,已知D是邊AC上一點,且AD=2CD,B=60°,a=2,a=3,求BD.

設計意圖:變式5至變式8使得問題進一步深化,問題的求解對數學能力有了更高的要求,通過問題的解答過程可以有效鞏固“四基”,發展“四能”,最終達到提高解題能力,發展數學素養的目的.
非營利組織一般都是以綠色營銷模式為主,不斷宣傳和加強民眾的綠色環保觀念,非營利組織會要求在各種類型的公共服務以及產品的設計、研發、量化生產和消費等環節,都需要考慮到對環境的影響和社會公眾的長遠利益。所以,在低碳營銷模式的發展過程中,非營利組織應該要積極配合有關政府部門的工作,以節約能源和保護環境為主旨,大力宣傳低碳營銷模式的理念。[4]從社會公眾的角度考慮,非營利組織幫助消費者建立低碳消費觀念,同時也幫助企業專注于低碳技術的研發生產和營銷,促使消費者深入細致了解低碳營銷模式的優勢所在,更加自主地選擇使用低碳產品,促使整個社會步入低碳經濟的可持續發展的道路。
2.4 基于一題多解拓寬解題思路培育創新意識
變式9 在△ABC中,已知D是邊BC上一點,且BD=2DC,AD=2,A=60°,求△ABC面積的最大值.
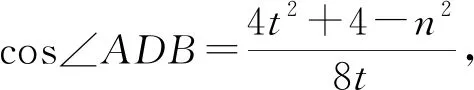

評注:解法1是本題的常規解法,也是眾多學生容易想到的方法,但解答過對運算求解能力有比較高的要求;解法2結合平面向量基本知識,基于向量這個重要的數學工具使得問題解答過程思路清晰、邏輯推理過程簡潔,優化運算并提高解題效率的作用.
設計意圖:從不同角度整合不同知識點對同一個問題進行深化拓展,引導學生開展問題求解訓練,在實際問題的解決過程中感悟數學問題的本質,尋找知識間的邏輯聯系,優化學生思維,拓寬解題思路,培育創新意思.
3 高考鏈接

A.6 B.5 C.4 D.3

(1)求B;(2)若△ABC為銳角三角形,且c=1,求面積的取值范圍.
真題4 (2018年全國卷Ⅰ)在平面四邊形ABCD中,∠ADC=90°,∠A=45°,AB=2,BD=5.

設計意圖:高考題是命題專家智慧的結晶,高考題不僅有很好的選拔功能,同時也有很好的教學功能,是教與學的好素材.因此,通過對問題的求解,回顧基礎知識,構建知識體系后,再選取針對性較強的高考真題讓學生在不同情景中解決問題,通過對不同問題的解題實踐,提高學生的應變能力,增強學生學習數學的信心,訓練數學思維,培育理性精神和發展數學素養水平等.
4 結語
由于學生剛完成本單元新知識的學習,往往缺乏將知識點連成線,繼而織成面,應用所學知識解決實際問題的能力還有很大的提升空間,以問題的為導向的單元復習課教學模式是以問題為驅動,引導學生回顧并復習知識,構建知識體系,使知識系統化網絡化.通過對典型問題開展變式拓展并從不同角度思考問題、解答問題可有助于提升解題能力,培育創新意識,發展數學核心素養,最終達到預期的教學效果.

