基于小波分析的混凝土箱梁橋應變監測數據的超載信息識別

薛 剛，張憲法，孫曉燕，顧永強

（內蒙古科技大學 土木工程學院，內蒙古 包頭014010）

近幾十年來，健康監測技術在橋梁結構的使用、維護及加固改造方面起到十分重要的作用。小波技術在挖掘橋梁健康監測信息方面，有著獨特的優勢，可獲得信號在不同尺度上的“信息增量”。趙華等[1]利用小波變換研究了數值仿真信號及實橋測試信號的車軸信息識別問題，結果表明，小波變換能提高橋梁動態稱重系統的車軸信息識別精度。尤瓊等[2]利用小波有限元對移動荷載識別問題進行了仿真研究，結果表明，與傳統有限元模型相比，小波有限元模型以較少的單元在相同的識別時間內可獲得相近的移動力識別精度。夏樟華等[3]建立了由健康監測系統測得的應變響應與移動荷載的線性回歸方程，基于小波原理，提出了一種能有效應用于大跨度連續剛構橋的移動荷載識別方法。橋梁結構除了承受自重等恒載作用外，主要承受車輛的循環往復作用，當重載或超載車輛較為集中時，容易導致橋梁結構出現裂縫、橋面車轍甚至發生沉陷等破壞。按照國際公認的軸載換算方法，超限100%的貨車作用一次對路面的破壞，相當于標準軸載作用16次產生的破壞[4]，識別橋梁的車輛超重信息對在役橋梁的安全使用和及時維護都很有必要。

G210 線黃河公路大橋位于內蒙古自治區包頭與鄂爾多斯市的交界處，為預應力混凝土箱梁橋，該橋是連接包頭市白云鄂博與陜西等省通衢的重要組成部分。大橋全長831 m，上部結構采用一聯11 孔預應力混凝土變截面連續箱梁，橋跨組合為（50 m+9×80 m+50 m）+2×5.5 m，該橋于2003年建成通車，在內蒙古經濟建設中的地位舉足輕重。為保障橋梁的安全使用，2010年起，橋梁運營管理部門在該橋安裝健康監測與安全評估系統，采用實時監測、人工檢測和定期測評相結合的方式，掌握橋梁結構的工作性能和病害損傷信息，實現對橋梁營運狀態健康狀況的實時監測和安全評估。本文根據小波原理，提取橋梁健康監測系統中的海量應變數據并進行預處理，對其中的異常信息進行分析及研判，從中識別出由超重車引起的應變響應信息，可豐富大跨度橋梁車輛超載的辨識手段及提高辨識效率，為制定橋梁安全運營的對策提供依據。

1 應變監測結果及分析

1.1 測點布置

G210 線黃河公路大橋健康監測系統共設置測點108個，其中應變測點60個，溫度測點4個，支座截面和跨中截面靜應變監測位置如圖1所示。

圖1 健康監測系統中靜應變監測位置

采用振弦式應變計監測G210 線黃河公路大橋的應變，其內置的溫度傳感器可同時監測環境溫度，對應變予以溫度補償。為排除車輛及溫度效應對橋梁結構初始應變的影響，于凌晨2:00 至4:00 間埋置振弦式應變計，該時段橋梁上的交通流量少，可最大程度降低車輛荷載對應變測量值的干擾，另外，該時段的應變埋置點沒有陽光直射，箱梁內外溫度相同，可最大程度降低溫度效應對應變測量值的影響。

1.2 應變時程曲線特征分析

G210線黃河公路大橋縱向走位為南北向，選取由北向南第十跨跨中底板測點（后文簡稱為42#測點）應變作為研究對象。橋跨跨中底板的傳感器對隨機事件比較敏感，且受噪聲影響較小。每15分鐘采集一次數據，以天為單位，選取某一年的應變監測數據，將實時應變與本文2.1 節得到的初始應變作差，得到42#測點的應變時程曲線，如圖2所示。

圖242 #測點應變時程曲線

圖2表明，42#測點的監測應變比較完整，可認為該位置的振弦式應變計的工作狀態較為穩定。該測點應變的年度時程曲線呈正弦型，符合四季更迭規律，部分監測應變值有波動現象，呈現出振動強度大而出現次數少的特點。研究表明[5]，大跨度橋梁應變監測數據的波動現象主要由超重車過橋、大風、突發強烈振動或地震動所引起，這些致因引發不同特征的振動。

常規載重車輛通過橋梁時，結構產生振動，應變時程曲線驟然增大后迅速減小，超重車輛通過橋梁時，產生的振動幅度為正常車輛產生振幅的數倍[6]。強風作用下橋梁結構的動態反應非常復雜，可引發風和結構物的相互作用，應變信號漂移且沒有規律。地震動、人工爆破等突發的隨機振動事件，引發的橋梁振動周期短且振幅大。

對G210 線黃河公路大橋的使用狀況進行調查[7]，在所考慮的時間段內，橋梁周圍未突發劇烈振動及地震等偶然事件，也沒有暴風作用，可以人為風荷載引起的效應遠小于車輛荷載引起的效應。

1.3 應變監測數據的奇異值處理

傳感器跳變產生的異常表現為監測數值較大且集中出現，該現象稱之為奇異值簇集現象[8]，如圖3中某年度3月14日至16日的監測數據所示。通過分析各種異常事件的特點可對監測數據進行數據預處理。

圖3 監測數據的奇異值簇集

圖2中部分數據變化劇烈或出現奇異值簇集現象，并非由車輛荷載引起，稱為奇異值異常。通常情況下，某采樣點與其相鄰采樣點差值絕對值大于200 με，或該采樣點出現奇異值簇集現象，該采樣點信號被視為奇異值異常。根據監測信號識別超重車輛信息，進而預測全年的超重車輛信息為概率問題。在所考慮的時間段內，橋梁周圍無劇烈振動、地震、暴風等事件，所以，對奇異值異常數據做剔除處理，預處理后的應變監測值異常考慮為由車輛荷載所產生。

采用MATLAB軟件對42#測點的監測數據進行編程預處理，預處理后的應變時程曲線見圖4。

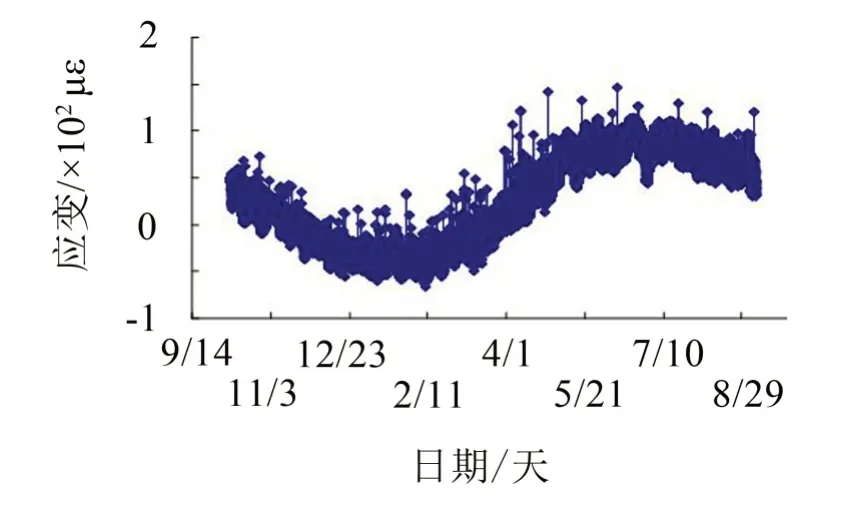
圖4 42#測點預處理后的應變時程曲線

一般而言，營運階段的大跨連續箱梁的應變主要由自重荷載、溫度荷載、車輛荷載及風荷載綜合作用產生的，就荷載特點而言，自重荷載、溫度荷載的變化較為緩慢，而車輛荷載和風荷載作用時間短，且無規律可循，隨機特征更加明顯。橋梁結構某點的總應變可表示為

式中：εT,t+εR,t，εC為混凝土的長期收縮和徐變應變，混凝土的收縮和徐變在施工及成橋前期比較明顯，大約經過5年～10年混凝土的收縮徐變達到一個極值，黃河大橋2003年建成通車，本次橋梁健康監測距離建橋通車已接近10年，混凝土收縮徐變已基本完成。εM為結構自重荷載，該值在橋梁結構總應變值ε(t)中的比重最大。

εT,t為熱應變，是由溫度效應而引起的應變，在橋梁受力過程分析中非常復雜，本次橋梁結構監測應變數據每15分鐘采集一次，15分鐘內的溫度效應變化微小，不至引起應變監測值ε(t)的突變。

引起應變值εR,t的隨機荷載主要包括車輛荷載、風荷載等。研究發現[9-10]，風荷載對橋梁結構的作用非常復雜，考慮本橋橋址的環境和橋型，風荷載產生的橋梁結構受力與車輛荷載相比相對較小。汽車過橋時，汽車荷載會使得應變監測數據組成部分εR,t產生激烈變化，該值相對于相鄰采樣點表現出反常的特征，車輛荷載越大異常現象越顯著，該特點可用于在應變監測數據中識別出超重車輛。

2 小波技術在信號異常診斷中的應用

2.1 小波檢測信號的基本原理

由式（1）可知，總應變ε(t)是由3種不同的應變組成，3種應變具有不同的時間尺度，小波分析對于分解不同頻率、尺度的數據具有明顯優勢[11]。利用小波變換對信號進行多尺度分析，在信號出現突變時，小波變換后的系數具有模量極大值，通過檢測模量極大值點可確定異常事件發生的時間點。

對應變數據進行離散小波分解[12]，如式（2）所示：

式中：cJclk為持續荷載作用下收縮徐變的尺度系數，dJct為溫度引起的應變變化的小波系數。小波分解系數djk與ε(t)的組成部分（式(1)中的εR,t）變化同步。

正常情況下應變ε(t)隨時間變化光滑，突變將導致ε(t)變化不連續，相應的djk比鄰近的點要大的多。小波系數djk代表數據的波動程度，而波動程度的大小判定則可以通過與一個關鍵閾值進行比較實現，超過該關鍵閾值即被認為應變類數據產生突變，通過記錄那些已識別的比閾值大的小波系數的位置，可將潛在的異常信號可從應變時間系列中提取出來。關鍵閾值按式（3）計算[13]：

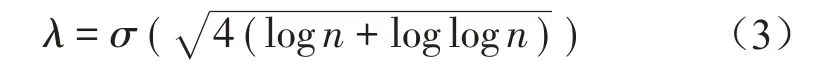
式中：σ是反映監測數據噪聲水平的參數，按式(4)計算[14]：

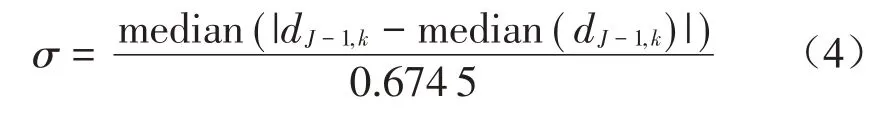
式中：J=log2(n)，n為信號的長度，median(dJ-1,k)為數據序列dJ-1,k的中位數。

2.2 信號超重信息的小波診斷結果

選取第十跨跨中底板箱梁內側底板應變數據進行分析。對預處理后的實測數據進行小波分解并獲得相應小波系數，并將小波系數與關鍵閾值進行比較，識別超重車，具體技術路線見圖5。

圖5 超重車輛小波識別技術路線

以第42#測點某個月的數據為例進行詳細說明，該時間段實測應變值經預處理后，如圖6所示。

利用MATLAB的Db(4)小波程序，將42#測點經預處理后某月份的實測應變監測數據進行兩層分解，得到細節系數，圖7中較深顏色線代表監測信號，較淺顏色線表示小波分解第2層細節信號。

提取分解出的第2層細節信號，并根據式（3）計算得到關鍵閾值λ為4.28，將小波細節系數與關鍵閾值進行比較，記錄超過關鍵閾值的細節系數所對應的應變信號并記錄其位置。圖8展示了300個應變監測信號的細節系數及識別出的奇異值點。

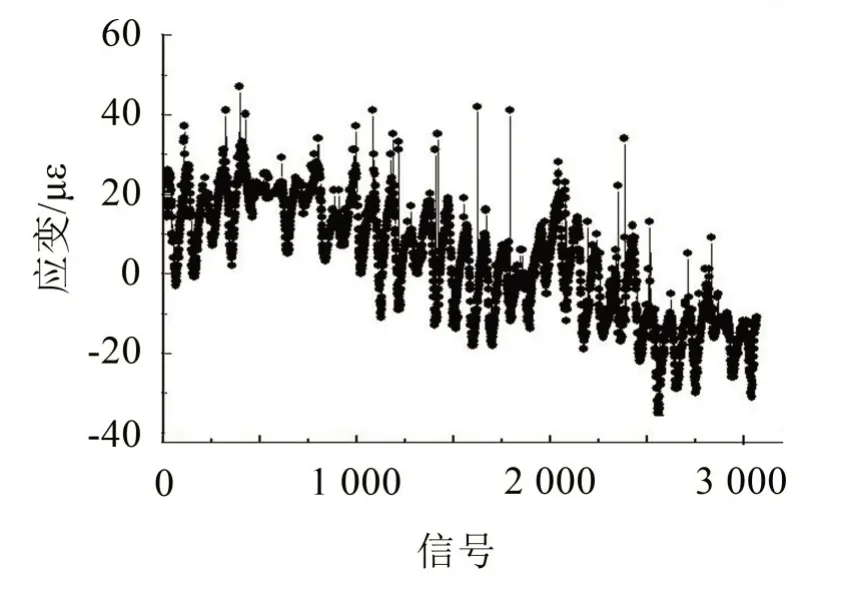
圖6 42#測點經預處理后的某月份的應變監測數據

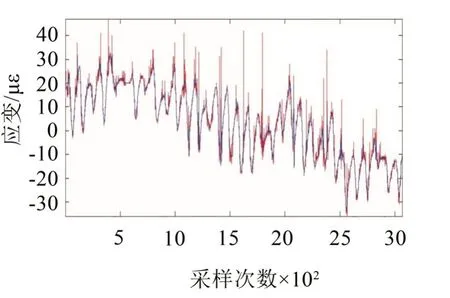
圖7 42#測點某月份應變信號及其小波細節系數

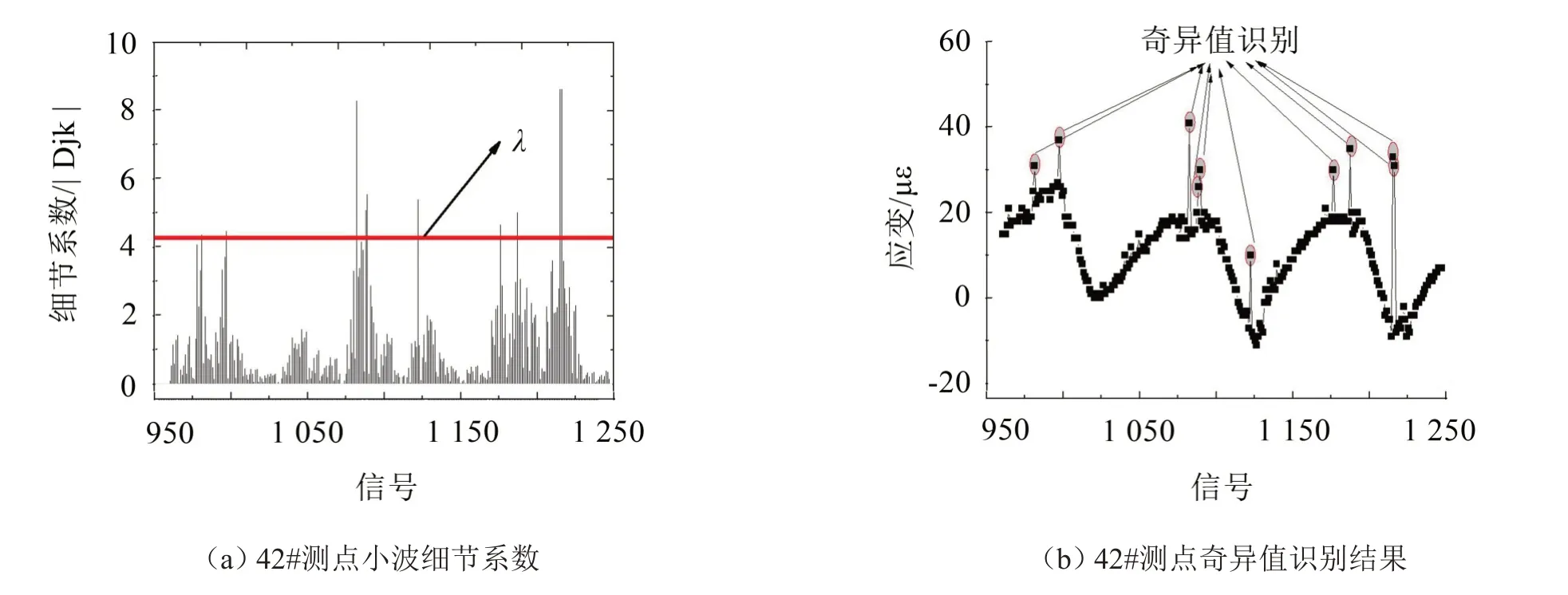
圖8 42#測點某時間段應變小波細節系數及奇異值識別結果

圖8中識別出的異常點跳躍方向一致，反映了識別數據的可靠性。對從42#測點所提取時間段的監測數據進行統計并識別，得到467個奇異值。

車輛荷載作為動荷載加載在橋梁結構是瞬時加載，正常車輛經過橋面時，橋梁結構會產生應變值的改變，表現為由弱變強再轉弱，重型車輛過橋時引起的橋梁振動幅度通常是正常通車的數倍，即重型車輛通過橋面時跨中底板的應變值比車輛正常通行時引起的應變值大，這就為識別超重車輛提供依據。

2.3 應變閾值界定

預應力混凝土橋梁結構營運階段受力比較復雜，不考慮溫度效應時，橋梁結構主要承受預應力、自重荷載及車輛荷載的作用。為獲得車輛荷載作用下橋梁結構產生的應變，建立有限元模型，并施加預應力、自重及車輛荷載，將有限元計算結果減去同時施加預應力及自重作用時產生的應變，兩者差值即為車輛荷載產生的應變，42#測點在車輛荷載作用前的壓應變值為-502.83 με，將其作為初始值。依據該橋設計時使用的《公路橋涵設計通用規范》（JT J021－1989），并參考現行規范，考慮3種運營工況：工況1為一輛QC-20重車（55噸）加載；工況2為兩輛QC-20 主車（30噸）并排加載；工況3為符合實際車流狀況的車隊加載，模擬車輛正常行駛過程。3種工況車輛軸距、輪距及載重參見文獻[7]。3種工況下橋梁第十跨跨中底板應變響應如圖9所示。

圖9 3種工況下第十跨跨中底板應變響應

將3種車輛運行工況下的有限元計算結果減去應變初始值，可得到3種工況下車載在該測點的靜應變分別為11.02 με、10.70 με 和9.27 με。考慮該橋車輛的沖擊系數為0.116[15]，取工況1 測點的靜應變11.02 με 算得該測點處車輛作用的應變幅閾值，為11.02×(1+0.116)=12.29 με，超過該閾值的應變為超重車輛產生。

圖10 不同加載情形跨中底板應變響應

車輛行駛速度為12 m/s，整個橋長831 m，走完全橋不超過68 s，而傳感器的采樣周期為15分鐘一次，正常載重的汽車經過時被監測系統捕捉到的概率非常小，汽車越重捕捉到的概率越大。圖10為不同載重情況下測點的應變響應，由此可知，一輛兩倍標準荷載的超重車產生的應變值超過閾值的時間間隔是2.13 s，按照15分鐘的采樣間隔時間計算，超重車被捕獲的概率為2.13÷(15×60)=0.237 %。

2.4 超重車輛識別及數量估計

樣條插值具有收斂快的優勢，同時可在非線性插值中增加節點來改進光滑度。本文采用三次樣條插值原理，利用MATLAB軟件編程計算出該奇異值時間點的“理論值”，將奇異值與“理論值”做差后與應變幅閾值比較，若超過該應變幅閾值，則認為這是由于超重車輛作用而產生的。

基于MATLAB識別出該時間段共存在146個應變幅超過應變閾值，超出閾值的應變幅的概率密度柱狀圖為圖11，該概率分布符合一般活荷載的極值I型分布，可用式（5）進行函數擬合：

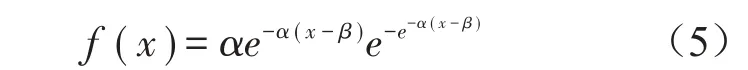
式中：α表示尺度參數，β表示位置參數。擬合結果為圖11中的紅顏色線，該擬合曲線較好地反映超出閾值的應變幅的概率分布，擬合效果較好。此時，α為0.234 45，β為25.635 8。

圖11 超出閾值的應變幅概率及擬合曲線

圖11所示的擬合曲線較好地反映了超出閾值的應變幅的概率分布規律，說明超重信息的識別結果是可靠的。根據本文圖10可知，超重車信息被捕獲的概率為0.237%，按照本文選取的330天的應變時程，可概率估算出該橋在本文所取年份內經過的超重車為67 510輛，日均超重車約187輛，與在G210線黃河大橋收費站同期歷史記錄基本相符。

3 結語

本文提取G210 線黃河大橋健康監測系統中的海量應變數據，對第十跨跨中底板42#測點的數據進行分析，利用小波原理識別出超重信息，得出以下結論：

（1）自重、收縮徐變效應以及溫度效應產生的應變在監測過程中變化緩慢，不會產生應變信號的突變，預處理后的監測數據的奇異值由車輛過橋引起。

（2）利用小波原理對橋梁的應變監測數據進行兩層小波分解，確定其關鍵閾值，將小波細節系數與關鍵閾值進行比較，可對超出關鍵閾值的應變信號進行奇異值識別，識別效果較好。

（3）依據現行規范設置不同荷載工況，得到重車駛過42#測點時的應變幅閾值為12.29 με。根據有限元分析得到超重車產生的應變值超過閾值的時間間隔是2.13 s，按照本文選取的監測時間段，從概率上估算出該年份日均超重車輛為187輛，與黃河大橋監測站同期的歷史記錄基本相符。