考慮尾流效應(yīng)的新月形覆冰四分裂輸電線舞動穩(wěn)定性

鄒 明，劉小會,2，蔡萌琦，伍 川，葉中飛，張 博

（1.重慶交通大學(xué) 土木工程學(xué)院，重慶400074；2.重慶交通大學(xué) 省部共建山區(qū)橋梁及隧道工程國家重點實驗室，重慶400074；3.成都大學(xué) 建筑與土木工程學(xué)院，成都610106；4.國網(wǎng)河南省電力公司 電力科學(xué)研究院，鄭州450052）

在風(fēng)載荷作用下覆冰輸電線會發(fā)生低頻大幅度的自激振動，覆冰是輸電線路大幅舞動的重要因素之一，也是難以解決的問題之一。舞動發(fā)生時輸電線會產(chǎn)生豎向的大幅振動，振幅有時會達到1 m～2 m，會導(dǎo)致金具的磨損和破壞、螺栓的松動和脫落、間隔棒的損壞、輸電線的斷裂，嚴重時甚至?xí)霈F(xiàn)輸電塔倒塌，引起供電系統(tǒng)停運，給人們的生活和經(jīng)濟造成了巨大的損失[1]。

在輸電線舞動研究領(lǐng)域，國際上廣泛接受3 大舞動理論，第一個是美國學(xué)者Den Hartog 提出的單自由度垂直舞動理論[2]；第二個是加拿大學(xué)者Nigol等提出的扭轉(zhuǎn)舞動理論[3]；第三個是日本學(xué)者Yu 等提出的偏心慣性耦合舞動理論[4]。

在3 大舞動理論的基礎(chǔ)上，國內(nèi)外的專家學(xué)者也做了大量的研究工作；例如，樓文娟等[5]基于特征值攝動法，在試驗中改變橫扭自振頻率，提出覆冰分裂導(dǎo)線橫扭穩(wěn)定性判斷條件。謝增等[6]研究了分裂導(dǎo)線扭轉(zhuǎn)剛度的問題，提出了一種等效單導(dǎo)線舞動模型，用數(shù)值模擬的方法預(yù)測了輸電線的舞動。嚴波等[7-8]通過數(shù)值模擬的方法對四分裂輸電線馳振進行了數(shù)值仿真，基于靜態(tài)模擬法，對覆冰四分裂導(dǎo)線進行了風(fēng)洞模擬試驗。張路飛等[9]利用有限元軟件ABAQUS建立了連續(xù)檔覆冰輸電線模型，考察了不同檔距和檔數(shù)對輸電線舞動的影響規(guī)律。以上4位學(xué)者主要通過數(shù)值模擬的方法對輸電線的舞動進行了研究。王少華在Den Hartog舞動判斷準則的基礎(chǔ)上更加準確地推導(dǎo)了臨界風(fēng)速隨風(fēng)攻角的變化規(guī)律[10]，在推導(dǎo)的過程中建立了2 自由度的模型，忽略了扭轉(zhuǎn)振動。芮曉明等[11]考慮脫冰效應(yīng)，研究了阻尼對舞動特性的影響。樓文娟等[12]建立了三維非線性耦合效應(yīng)連續(xù)體輸電線舞動動力學(xué)方程。

綜上所述，現(xiàn)在關(guān)于導(dǎo)線舞動機理大多考慮了水平、豎直、扭轉(zhuǎn)3個方向上舞動的耦合。目前，單導(dǎo)線舞動的研究較為成熟，對四分裂導(dǎo)線的舞動模型研究較少，但是在實際工程中，四分裂輸電線更容易發(fā)生舞動，且大多數(shù)對于四分裂導(dǎo)線的研究沒有考慮尾流效應(yīng)對分裂導(dǎo)線的影響，這與實際工程不相符，且研究集中于數(shù)值模擬法，所得結(jié)論不具有普遍適用性。本文基于擬靜態(tài)理論，建立新月形覆冰四分裂導(dǎo)線舞動的3 自由度振動模型，在考慮尾流效應(yīng)的條件下從理論上推導(dǎo)了系統(tǒng)穩(wěn)定判別式；研究了線路結(jié)構(gòu)參數(shù)對新月形覆冰四分裂導(dǎo)線穩(wěn)定性的影響，使用MATLAB軟件基于穩(wěn)定判別式計算出覆冰四分裂導(dǎo)線的臨界風(fēng)速。所得結(jié)果對于覆冰四分裂輸電線防舞具有重要的參考價值。

1 建立力學(xué)模型

架空輸電線離地面有一定的高度，地面物體對風(fēng)速的影響很小，所以本文的力學(xué)舞動模型是在穩(wěn)定風(fēng)作用條件下建立的。由于空氣尾流效應(yīng)的影響，四分裂導(dǎo)線處于風(fēng)速分布不均勻的風(fēng)場中，每一根子導(dǎo)線受到的空氣動力不同，在計算四分裂導(dǎo)線整體所受到的風(fēng)荷載時不能用一根子導(dǎo)線風(fēng)荷載的4倍來等效。本文考慮單檔導(dǎo)線的舞動，假設(shè)風(fēng)速沿線路方向是不發(fā)生改變的；輸電線覆冰的形狀和厚度沿線路方向是不變的。基于上述的假設(shè)，可以把覆冰四分裂導(dǎo)線舞動的復(fù)雜模型簡單化，通過模態(tài)截斷法就可以將連續(xù)體振動的偏微分方程轉(zhuǎn)換為一個橫斷面沿著3個方向振動的常微分方程。分析振動穩(wěn)定性的3 自由度模型如圖1所示。假設(shè)穩(wěn)定風(fēng)從左往右流經(jīng)覆冰導(dǎo)線，風(fēng)速大小為U。導(dǎo)線在水平、豎直和扭轉(zhuǎn)方向的約束剛度分別是Kz、Ky和Kθ。圖中r是子導(dǎo)線中心與轉(zhuǎn)動中心之間的距離，H是覆冰厚度。

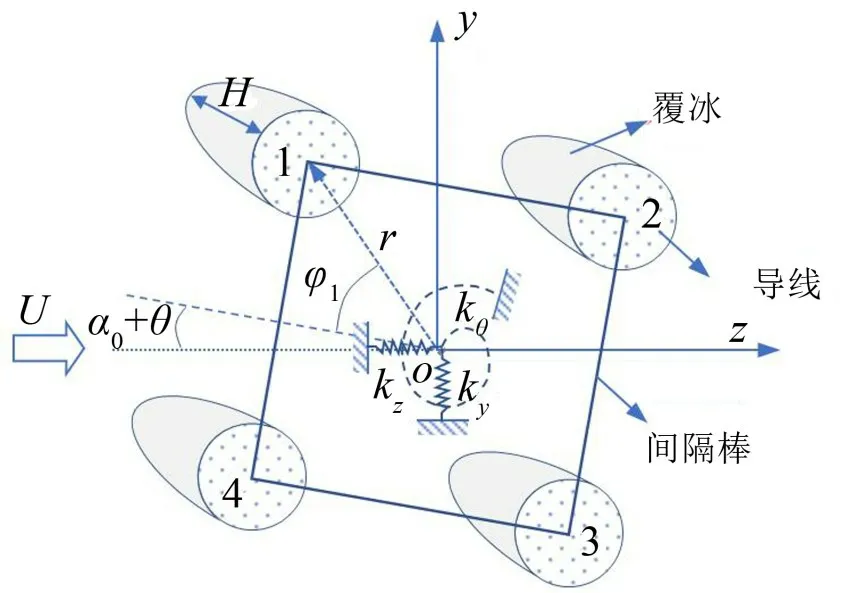
圖1 覆冰四分裂導(dǎo)線橫截面模型

其中：α0為初始風(fēng)攻角；θ為動態(tài)的扭轉(zhuǎn)角，隨時間而改變。子導(dǎo)線橫截面中心在整體坐標系中的坐標為

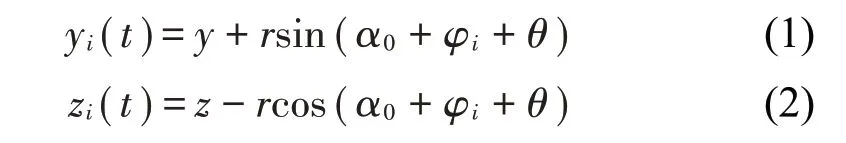
式中：y、z是四分裂導(dǎo)線中心在整體坐標系中的坐標值，i為導(dǎo)線的分裂數(shù)，i取1、2、3、4。φi是分裂導(dǎo)線中心和子導(dǎo)線中心連線與間隔棒之間的夾角，φi取值為φ1=45°;φ2=135°;φ3=225°;φ4=315°。

子導(dǎo)線隨時間變化的位移可以表示為

式中：v、u表示四分裂導(dǎo)線豎直和水平方向上的位移。對子導(dǎo)線的位移求1階導(dǎo)，得子導(dǎo)線的速度為

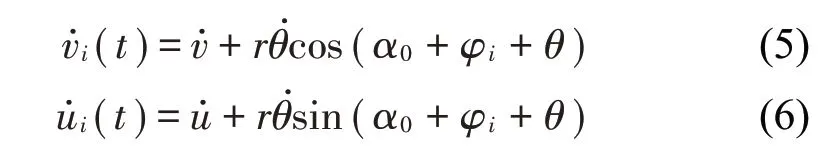
式中上標點表示對時間求導(dǎo)，由于在風(fēng)載荷作用下導(dǎo)線會產(chǎn)生相對運動，所以導(dǎo)線受到的阻力FD并不是沿水平方向，而升力FL也不是沿豎向；其方向會與水平或者豎直方向形成一個夾角。本文采用擬靜態(tài)假設(shè)計算覆冰四分裂導(dǎo)線受到的風(fēng)載荷，子導(dǎo)線與風(fēng)場之間的相對關(guān)系如圖2所示。

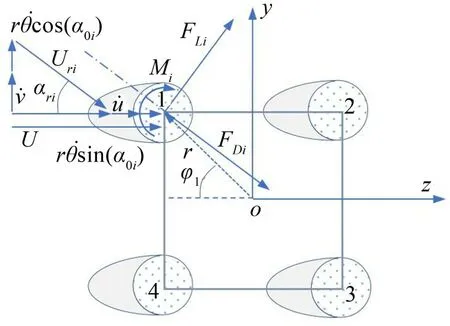
圖2 基于擬靜態(tài)假設(shè)的相對流場

FLi、FDi分別是子導(dǎo)線受到的升力和阻力；在風(fēng)載荷作用下，分裂導(dǎo)線中心沿水平運動會產(chǎn)生速度，分裂導(dǎo)線中心的扭轉(zhuǎn)運動也會產(chǎn)生水平向的速度分量，所以子導(dǎo)線在z方向的相對風(fēng)速為

分裂導(dǎo)線中心沿豎向運動時會產(chǎn)生速度˙，分裂導(dǎo)線中心的扭轉(zhuǎn)運動也會產(chǎn)生豎向的速度分量，所以子導(dǎo)線豎向的相對速度為˙+因此，實際的相對風(fēng)速Uri為

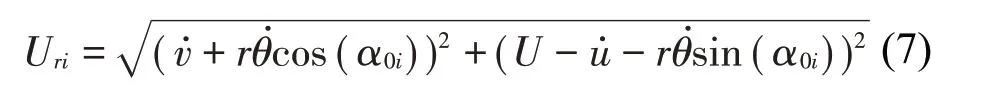
式中α0i=α0+θ+φi，子導(dǎo)線相對風(fēng)攻角αi可以由以下式計算：

式中：αri是導(dǎo)線運動速度變化引起的相對風(fēng)攻角改變量。覆冰子導(dǎo)線受到的與實際風(fēng)速平行的氣動阻力FDi、與實際風(fēng)速垂直的升力FLi和扭轉(zhuǎn)力矩Mi可以通過以下公式得到：

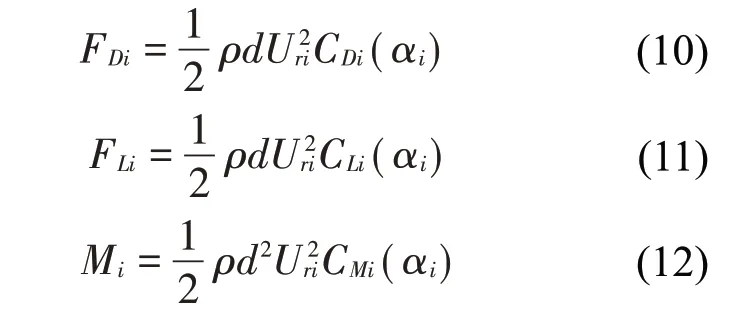
式中：ρ是空氣密度，d是覆冰裸導(dǎo)線直徑，CLi、CDi和CMi分別是覆冰子導(dǎo)線的升力系數(shù)、阻力系數(shù)和扭矩系數(shù)，可以通過風(fēng)洞試驗獲得。在穩(wěn)定風(fēng)作用下，處于風(fēng)場上游的子導(dǎo)線會吸收風(fēng)中的能量，在風(fēng)場的下流區(qū)形成尾流區(qū)域；處于下游風(fēng)場的子導(dǎo)線輸入風(fēng)速會低于處于上游風(fēng)場的子導(dǎo)線輸入風(fēng)速，同時下流風(fēng)場區(qū)域的湍流強度會增強；由于空氣尾流效應(yīng)，使得分裂導(dǎo)線所處的風(fēng)場風(fēng)速分布不均，從而造成各子導(dǎo)線的空氣動力系數(shù)不同。本文在研究導(dǎo)線舞動穩(wěn)定性時考慮了尾流效應(yīng)的影響。在計算覆冰導(dǎo)線的動態(tài)響應(yīng)時，需要將子導(dǎo)線的升力和阻力投影到z軸和y軸，可得：

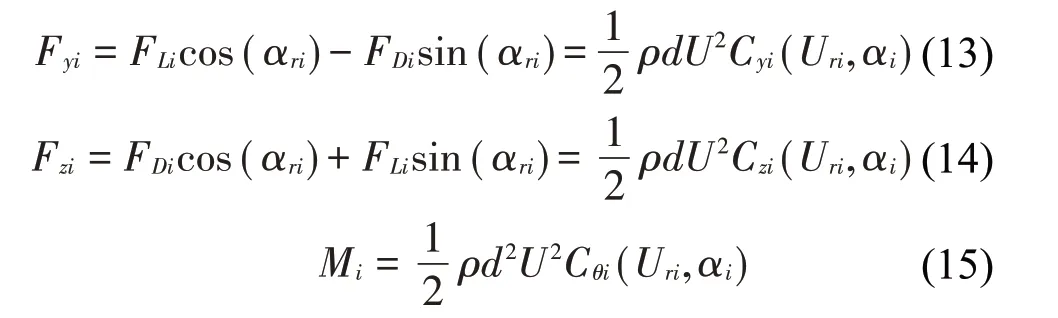
這里：Cyi、Czi和Cθi分別是子導(dǎo)線豎直、水平和扭轉(zhuǎn)方向的空氣動力系數(shù)，可以表示為

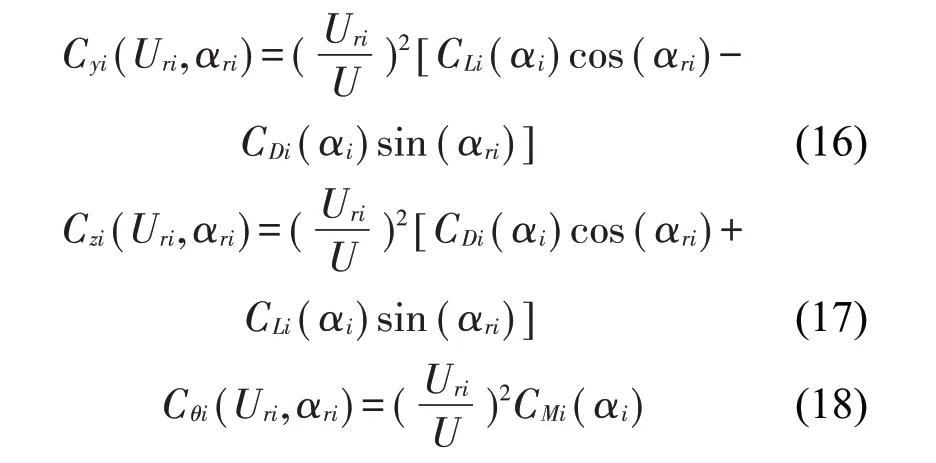
由于空氣尾流效應(yīng)的影響，四分裂導(dǎo)線整體風(fēng)荷載由各子導(dǎo)線風(fēng)荷載疊加等效得到。將4根子導(dǎo)線的升力、阻力和扭矩平移到四分裂導(dǎo)線的中心，根據(jù)平移定理可得：

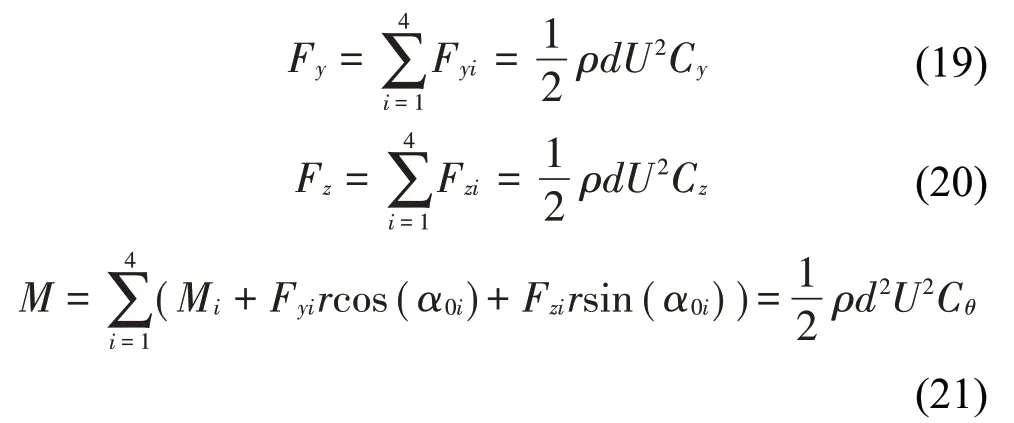
這里：Cy、Cz分和Cθ別是四分裂導(dǎo)線豎直、水平和扭轉(zhuǎn)方向的整體空氣動力系數(shù)，可以表示為

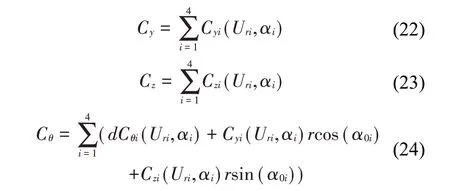
豎直、水平和扭轉(zhuǎn)方向的整體空氣動力系數(shù)可以在初始風(fēng)攻角α0處進行泰勒展開，其線性部分可以表示為

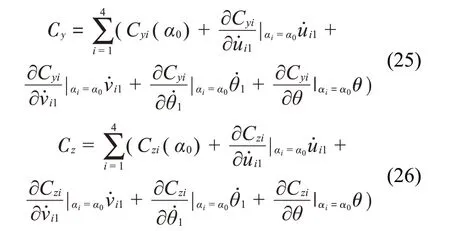
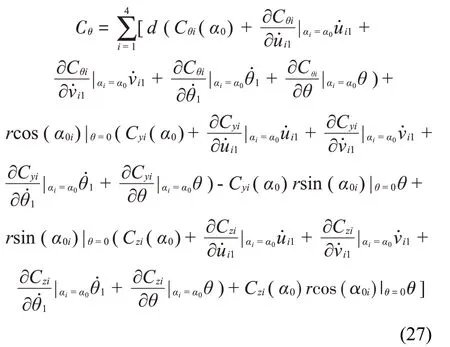
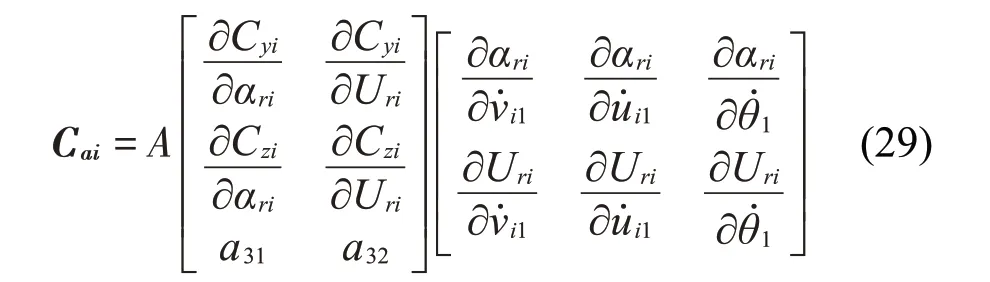
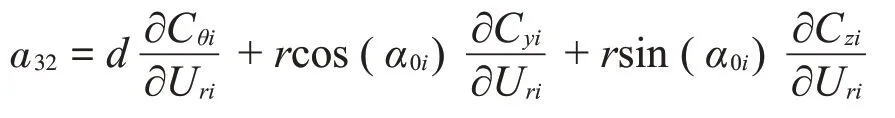
A=Kai為子導(dǎo)線載荷剛度矩陣，可以表示為

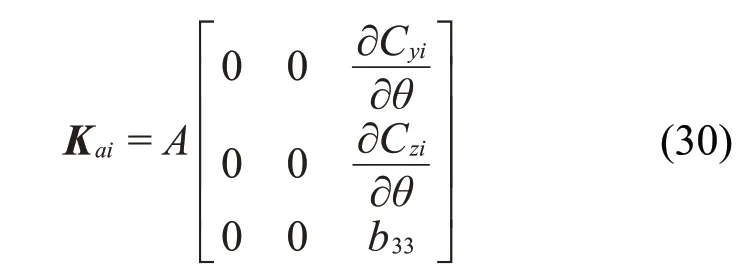
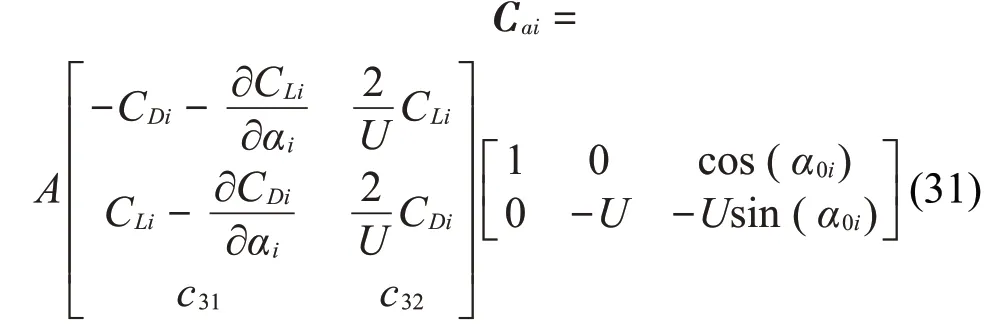
其中：

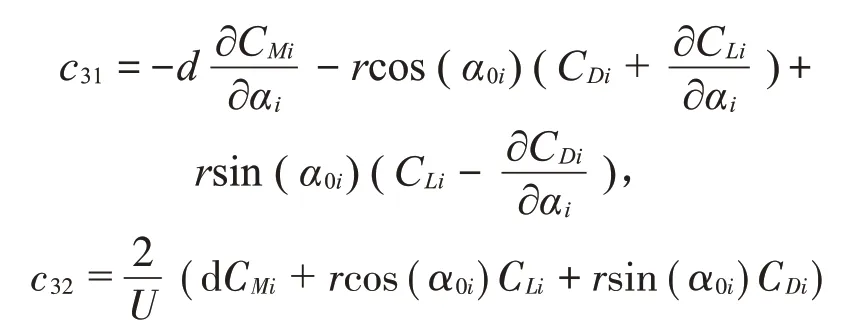
整理后可得空氣動力阻尼矩陣為

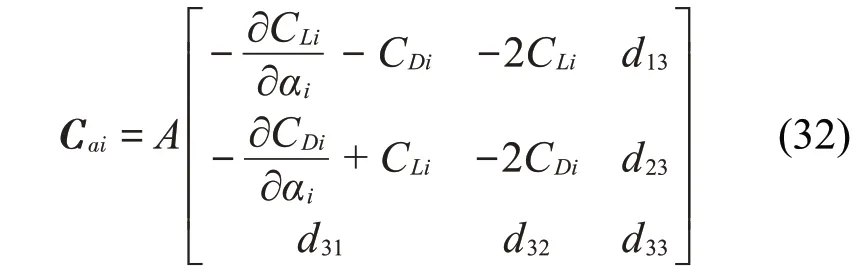
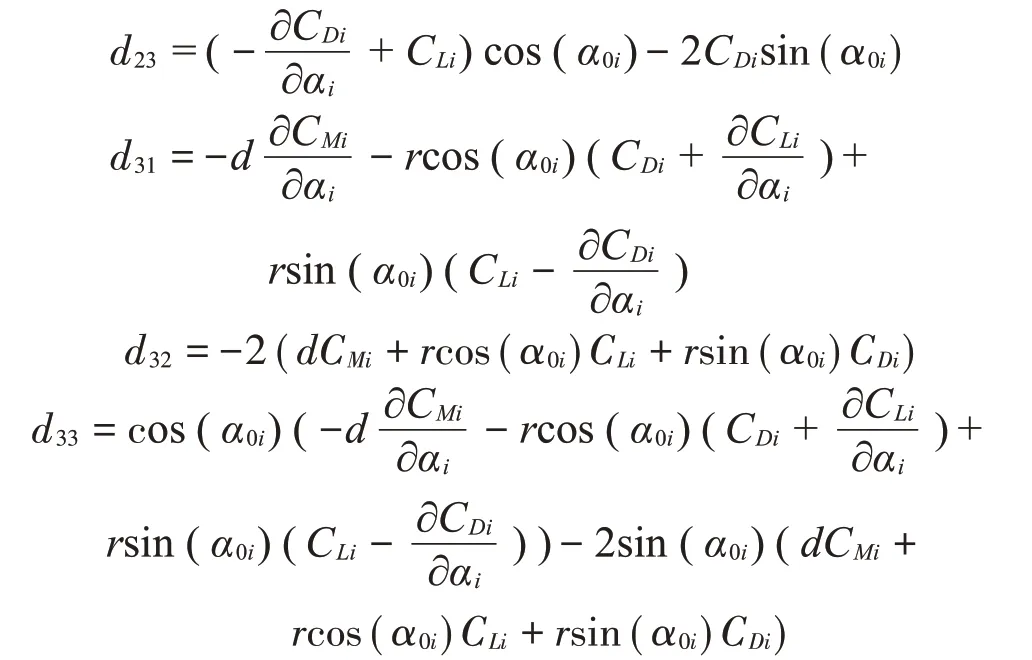
化簡后可得載荷剛度矩陣為

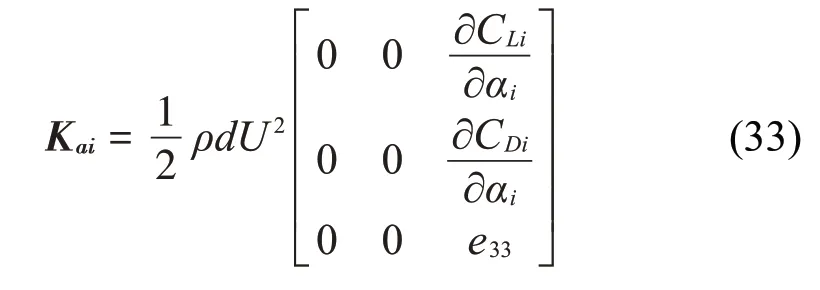
其中：

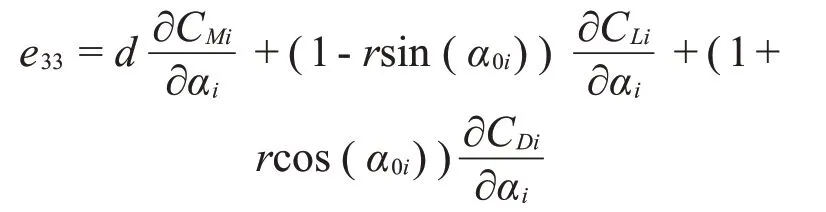
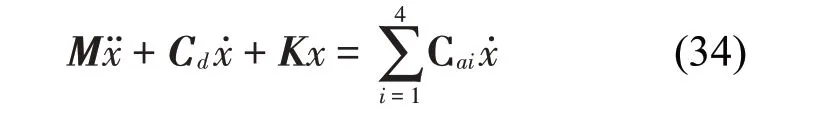
其中每一項表示的含義為

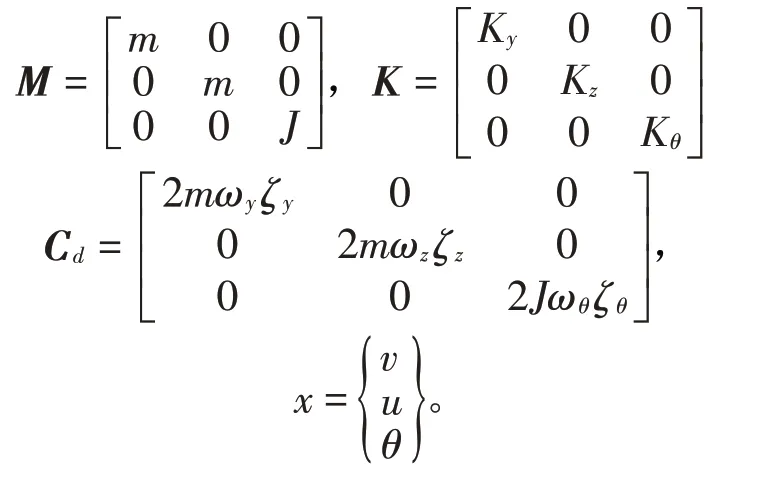
上式中覆冰四分裂導(dǎo)線單位長度的質(zhì)量為m，轉(zhuǎn)動慣量為J，3個自由度方向的阻尼比為ζy、ζz和ζθ，3個自由度方向的圓頻率為ωy、ωz和ωθ。根據(jù)式(34)可以得到系統(tǒng)的阻尼矩陣為

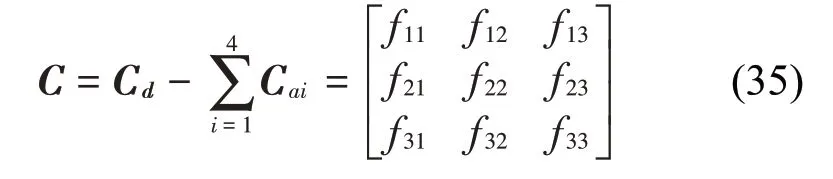
其中：

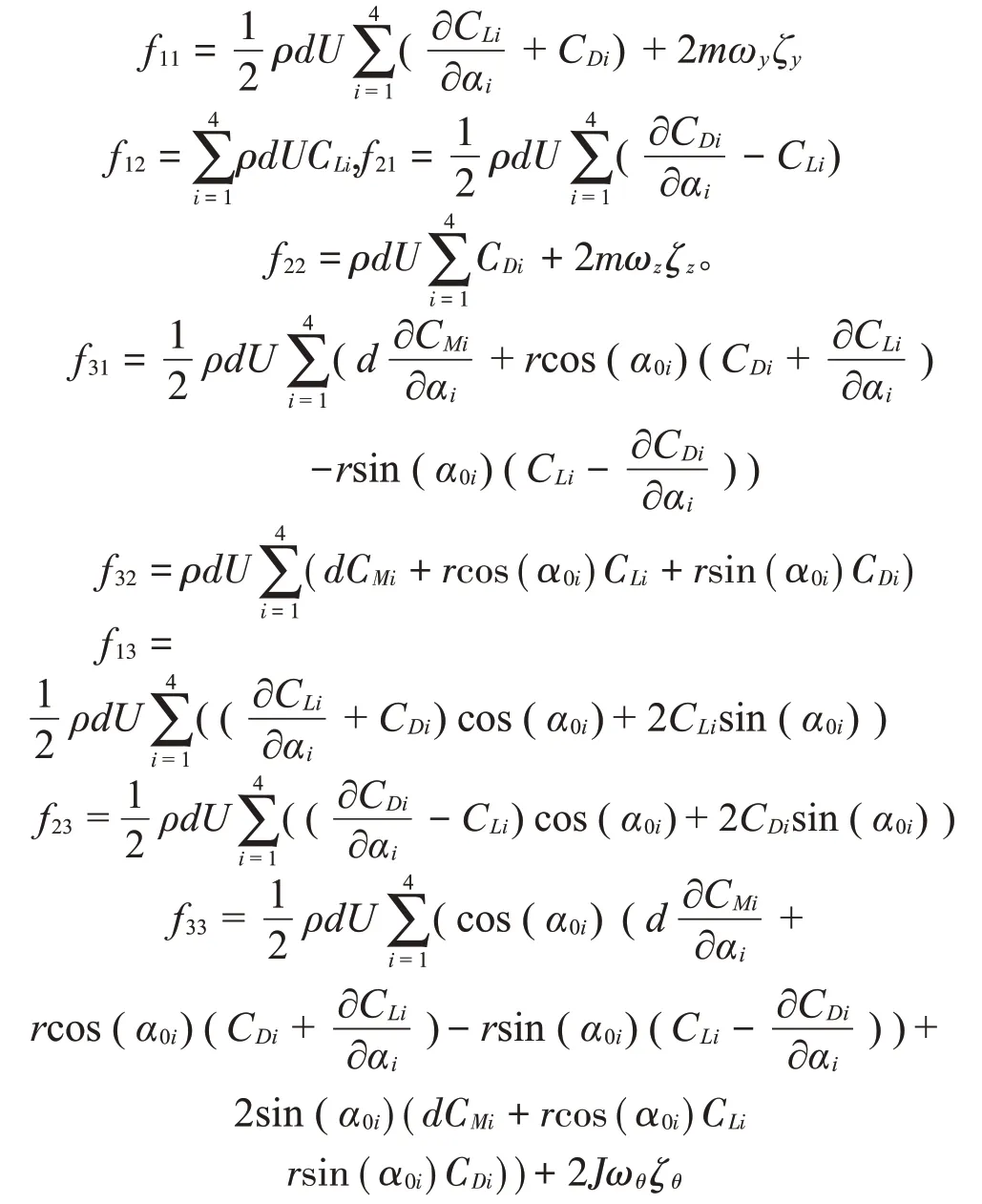
當僅考慮豎向運動時，系統(tǒng)阻尼矩陣中對角元素第一項f11即為Den Hartog判斷舞動的準則。當考慮扭轉(zhuǎn)誘發(fā)舞動時，系統(tǒng)阻尼矩陣中對角元素第三項f33即為Nigol 判斷舞動的準則。本文中基于3 自由度運動進行穩(wěn)定性分析，為了分析該系統(tǒng)的穩(wěn)定性，令X=Xeλ t，則特征多項式可以根據(jù)式(34)得到：

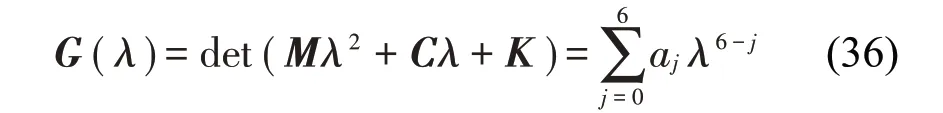
其中多項式的各個系數(shù)如下

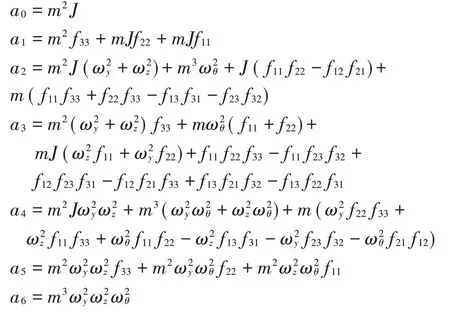
如果系統(tǒng)矩陣式(35)為正定矩陣，則這個動力系統(tǒng)穩(wěn)定。根據(jù)Rourh-Hurwitz準則，這個動力系統(tǒng)穩(wěn)定的條件是：

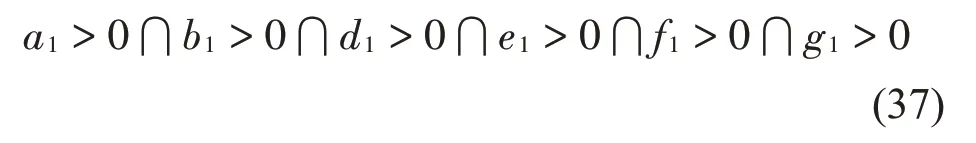
上式中各個參數(shù)可以表示為

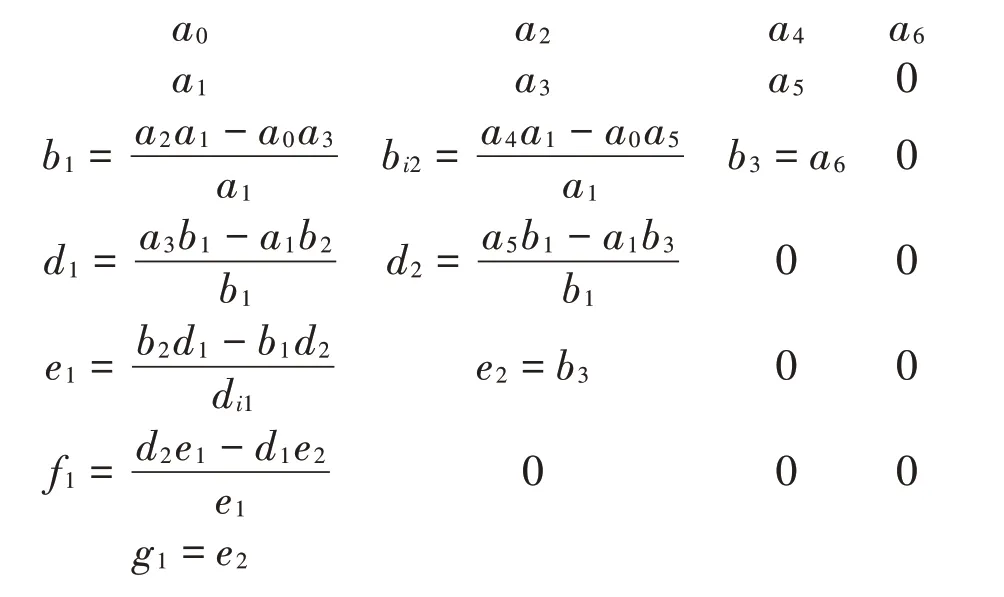
2 風(fēng)洞試驗與氣動特性分析

前一節(jié)完成了覆冰導(dǎo)線臨界風(fēng)速計算公式的推導(dǎo)，計算臨界風(fēng)速需要導(dǎo)線的空氣動力系數(shù)。為了獲取新月形覆冰四分裂輸電線的空氣動力系數(shù)，在中國空氣動力研究與發(fā)展中心低速所的1.4m×1.4m低速風(fēng)洞中進行了模型測試，這個風(fēng)洞外形如圖3(a)所示。測試模型如圖3(b)所示，四分裂導(dǎo)線模型由頂?shù)装暹B接在一起置于風(fēng)洞中，裸導(dǎo)線內(nèi)部安裝了測力天平，裸導(dǎo)線外部粘貼了新月形木材來模擬覆冰。當風(fēng)流經(jīng)過該覆冰導(dǎo)線時，測力天平可以測量出新月形覆冰四分裂導(dǎo)線所受到的升力FL、阻力FD和扭矩M。初始風(fēng)攻角為0°；每測量一次氣動載荷后，覆冰導(dǎo)線模型逆時針轉(zhuǎn)動5°，然后再測量一次氣動載荷，轉(zhuǎn)動范圍為0°～180°，四分裂導(dǎo)線的布置和風(fēng)攻角的變化如圖3(c)所示。

本實驗設(shè)置3種覆冰厚度進行試驗，覆冰厚度分別為12 mm，20 mm，28 mm；本文選取覆冰厚度為20 mm時的情況來分析空氣尾流效應(yīng)對各子導(dǎo)線氣動系數(shù)的影響，試驗風(fēng)速為14 m/s。通過風(fēng)洞試驗測得新月形覆冰四分裂導(dǎo)線空氣動力系數(shù)隨風(fēng)攻角變化曲線如圖4所示。

各子導(dǎo)線的空氣動氣系數(shù)大致是相同的，但是由于尾流效應(yīng)的影響，各子導(dǎo)線的空氣動力系數(shù)在局部會有不同。導(dǎo)線阻力系數(shù)隨風(fēng)攻角變化的曲線大致呈半波狀，當風(fēng)攻角α=0°時，此時導(dǎo)線的迎風(fēng)面積最小，阻力系數(shù)也最小；子導(dǎo)線3處于子導(dǎo)線1的尾流區(qū)，其阻力系數(shù)小于子導(dǎo)線1。當風(fēng)攻角α=45°時，子導(dǎo)線3、4處于子導(dǎo)線1、2的尾流區(qū)，其阻力系數(shù)降低。當風(fēng)攻角α=90°時，導(dǎo)線的迎風(fēng)面最大，阻力系數(shù)出現(xiàn)了峰值，子導(dǎo)線4處于子導(dǎo)線2的尾流區(qū)，其阻力系數(shù)明顯降低。同樣地，當風(fēng)攻角α=135°和α=180°時，對應(yīng)尾流區(qū)子導(dǎo)線的阻力系數(shù)均有所下降。

圖3 采用風(fēng)洞測試空氣動力系數(shù)

導(dǎo)線升力系數(shù)隨風(fēng)攻角變化的曲線大致呈正弦函數(shù)波狀，子導(dǎo)線2 在模型轉(zhuǎn)動過程中始終處于風(fēng)場的上游，幾乎不受尾流效應(yīng)的影響，其空氣動力系數(shù)變化曲線比較平緩，沒有突變；當風(fēng)攻角α=0°、α=90°和α=180°時，各子導(dǎo)線升力系數(shù)幾乎都為0。

導(dǎo)線扭矩系數(shù)隨風(fēng)攻角變化的曲線大致呈正弦函數(shù)波狀，當風(fēng)攻角α=0°、α=150°和α=180°時，各子導(dǎo)線扭矩系數(shù)幾乎都為0，且α=150°時，扭矩系數(shù)和升力系數(shù)相同。

3 臨界風(fēng)速計算

采用MTALAB編寫判斷和循環(huán)語句程序，將第2 節(jié)風(fēng)洞試驗所得的氣動系數(shù)和文獻[13]的導(dǎo)線頻率代入式(19)和式(21)，計算各種工況下不同舞動判斷準則的臨界風(fēng)速。關(guān)于覆冰四分裂導(dǎo)線的扭轉(zhuǎn)頻率還沒有得到大家公認的研究結(jié)果，為了使結(jié)果具有合理代表性，本文選取3個扭轉(zhuǎn)頻率值分別進行計算，即0.2 Hz、0.4 Hz 和0.6 Hz。現(xiàn)對計算的結(jié)果進行分析。

根據(jù)計算結(jié)果，選取覆冰厚度為20 mm、扭轉(zhuǎn)頻率為0.4 Hz、風(fēng)攻角為165°時3種不同舞動理論的臨界風(fēng)速來對比驗證本論文所提出的3自由度舞動判別準則。所得結(jié)果如圖5所示。正方形曲線代表基于Den.Hartog理論所確定臨界風(fēng)速，圓形曲線代表基于Nigol理論所確定臨界風(fēng)速，三角形曲線代表基于本文3-DOF理論所確定臨界風(fēng)速。從圖中可以看出基于Den.Hartog理論的臨界風(fēng)速隨頻率比值變化不大，其值在6 m/s～7 m/s之間。基于Nigol理論的臨界風(fēng)速不隨頻率比值變化，其值為8.2 m/s，Nigol理論只與扭轉(zhuǎn)頻率有關(guān)，所以其臨界風(fēng)速不會隨面內(nèi)和面外頻率比值變化，是一個定值。

基于本文3-DOF理論的臨界風(fēng)速隨頻率比值的增大而減小，其值在7.5 m/s～14.7 m/s之間，由于本文3-DOF理論與3個方向的頻率有關(guān)，考慮了3-DOF 之間能量的傳遞，其臨界風(fēng)速隨頻率比值變化明顯。當頻率比小于2時，根據(jù)本文3-DOF理論所確定臨界風(fēng)速大于根據(jù)Den.Hartog理論和Nigol理論確定臨界風(fēng)速；當頻率比大于2時，根據(jù)本文3-DOF理論所確定臨界風(fēng)速與根據(jù)Den.Hartog理論和Nigol理論所確定臨界風(fēng)速接近。

根據(jù)計算結(jié)果，選取覆冰厚度為20 mm，風(fēng)攻角為105°，在不同扭轉(zhuǎn)頻率下，采用本文3-DOF理論確定臨界風(fēng)速，所得結(jié)果如圖6所示。

從圖6中可以得出，扭轉(zhuǎn)頻率對臨界風(fēng)速影響較大；扭轉(zhuǎn)頻率為0.2 Hz和扭轉(zhuǎn)頻率為0.4 Hz時，臨界風(fēng)速最大相差3.5 m/s。根據(jù)3條曲線進行分析，隨著扭轉(zhuǎn)頻率的減小，其臨界風(fēng)速減小；扭轉(zhuǎn)頻率減小其扭轉(zhuǎn)剛度也會減小，導(dǎo)線馳振越容易發(fā)生。扭轉(zhuǎn)頻率為0.4 Hz和0.6 Hz時對應(yīng)的臨界風(fēng)速隨著頻率比的增大而減小。扭轉(zhuǎn)頻率為0.2 Hz時對應(yīng)的臨界風(fēng)速隨著頻率比的增大先增大后減小。

根據(jù)計算結(jié)果可知，選取扭轉(zhuǎn)頻率為0.4 Hz、風(fēng)攻角為90°，在不同的覆冰厚度下，采用本文3-DOF理論確定臨界風(fēng)速，所得結(jié)果如圖7所示。

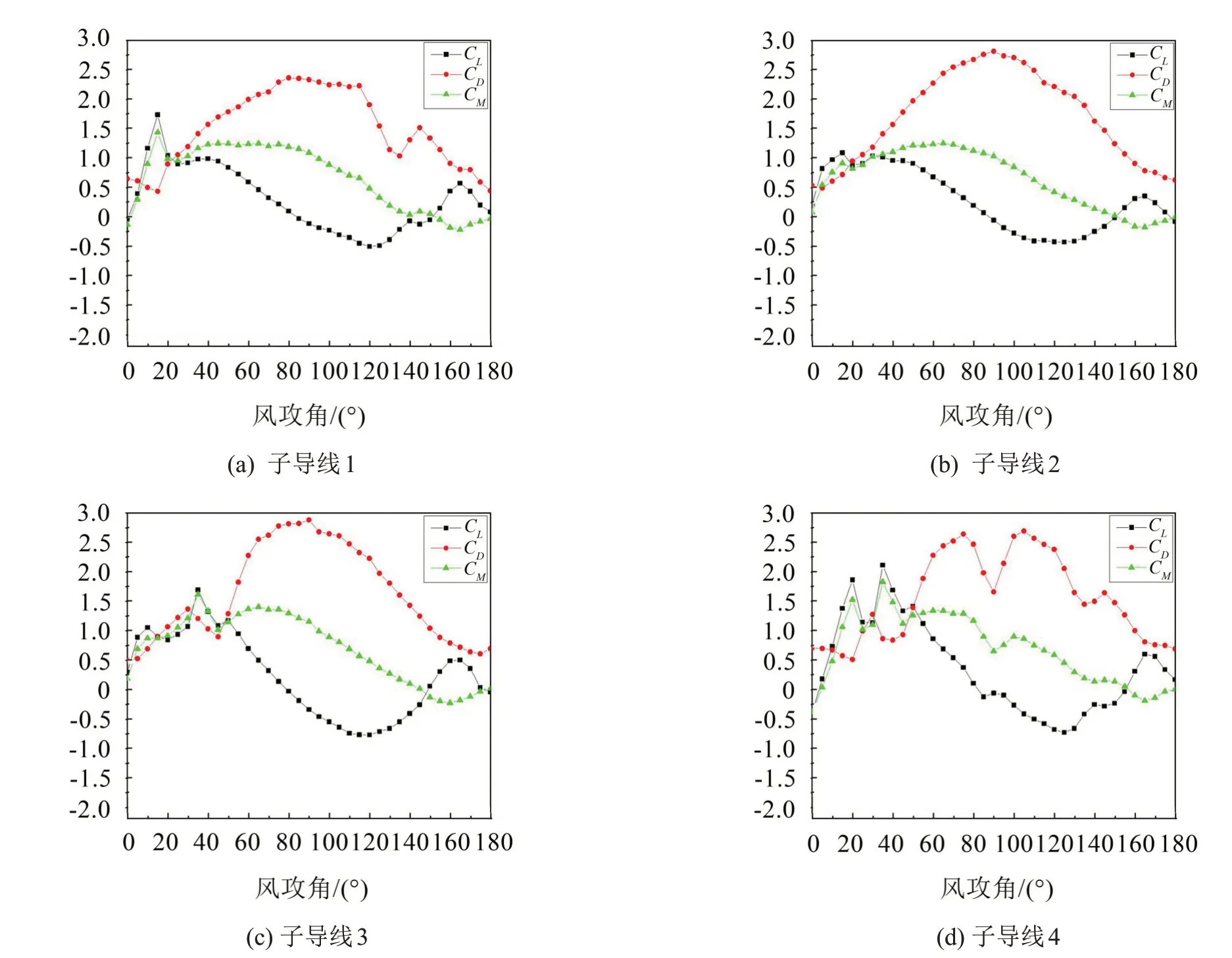
圖4 覆冰四分裂導(dǎo)線空氣動力系數(shù)

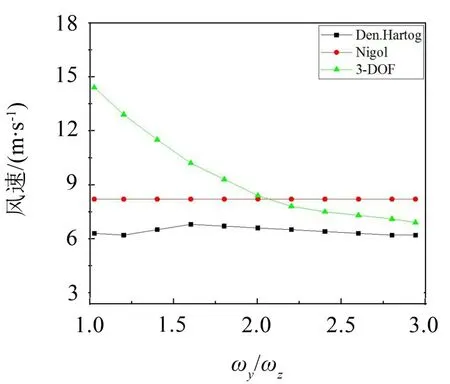
圖5 基于不同理論的臨界風(fēng)速對比

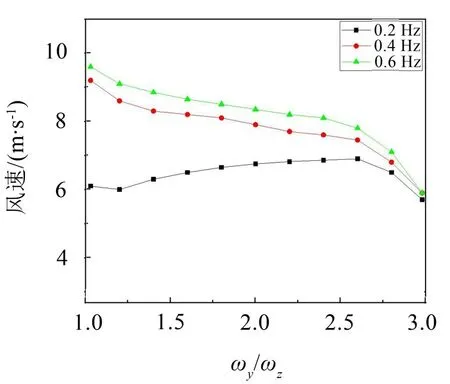
圖6 不同扭轉(zhuǎn)頻率下的臨界風(fēng)速對比

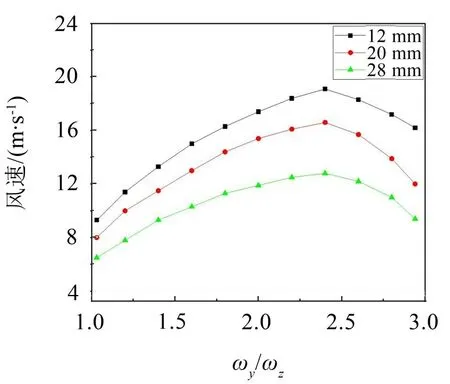
圖7 不同覆冰厚度臨界風(fēng)速

從圖7中可以看出，覆冰厚度對四分裂導(dǎo)線的臨界風(fēng)速影響較大。當覆冰厚度為12 mm和20 mm時，最大的臨界風(fēng)速差達到了7 m/s。隨著覆冰厚度的增大，其臨界風(fēng)速減小；由于覆冰厚度的增加，導(dǎo)線迎風(fēng)面增大，3個方向上的空氣動力系數(shù)均有所增大，使得導(dǎo)線更容易發(fā)生舞動。面內(nèi)外頻率比接近1和3時，線路最易發(fā)生舞動。

4 結(jié)語

本文通過基本建立3自由度新月形覆冰四分裂導(dǎo)線的力學(xué)模型，將空氣動力系數(shù)在初始風(fēng)攻角處進行泰勒展開，得到氣動荷載修正表達式。研究了覆冰四分裂導(dǎo)線在靜力風(fēng)作用下的舞動，忽略慣性耦合項以及載荷剛度項，得到3 自由度覆冰導(dǎo)線的振動方程。根據(jù)Rourh-Hurwitz穩(wěn)定準則，推導(dǎo)了動力系統(tǒng)平衡穩(wěn)定條件。在風(fēng)洞試驗中設(shè)置不同的覆冰厚度，通過風(fēng)洞試驗測得新月形覆冰四分裂導(dǎo)線在3個方向上的氣動系數(shù)。運用本文的3 自由度穩(wěn)定判別式計算出了不同的扭轉(zhuǎn)頻率和覆冰厚度所對應(yīng)的臨界風(fēng)速。考察了不同情況下臨界風(fēng)速隨面內(nèi)外頻率比變化特征。得到了以下結(jié)論：

（1）本文中所建的新月形覆冰四分裂導(dǎo)線的力學(xué)模型考慮了同一時刻子導(dǎo)線之間風(fēng)攻角的差異，更加真實地反映了每一根子導(dǎo)線對應(yīng)的位移和風(fēng)荷載。采用本文方法得到的3自由度舞動判斷準則更加詳細地考慮了豎向運動、橫向運動以及扭轉(zhuǎn)運動對臨界風(fēng)速的影響，更加符合實際工程情況。計算結(jié)果顯示，基于Den Hartog理論，可能發(fā)生舞動的風(fēng)攻角為15°、165°、170°；基于Nigol理論可能發(fā)生舞動的風(fēng)攻角為10°、165°、170°；基于本文3-DOF穩(wěn)定理論可能發(fā)生舞動的風(fēng)攻角為10°、55°、60°、70°、80°、95°、165°、170°；采用文中提出的理論確定的可能發(fā)生舞動的初始攻角范圍比Den Hartog理論和Nigol理論確定可能發(fā)生舞動的初始攻角的范圍更廣。因此，采用本文所提出的3-DOF 穩(wěn)定理論對線路防舞進行指導(dǎo)更合理。

（2）扭轉(zhuǎn)頻率對覆冰輸電線舞動的臨界風(fēng)速有顯著影響，隨著扭轉(zhuǎn)頻率的減小，其臨界風(fēng)速減小；扭轉(zhuǎn)頻率減小意味著其扭轉(zhuǎn)剛度也會減小，導(dǎo)線越容易發(fā)生舞動。因此在線路設(shè)計中應(yīng)該選取能導(dǎo)致較高扭轉(zhuǎn)頻率的線路參數(shù)來進行防舞設(shè)計。

（3）覆冰厚度對輸電線舞動的臨界風(fēng)速有顯著影響，隨著覆冰厚度的增大，其臨界風(fēng)速減小。在線路防舞設(shè)計時要特別注意覆冰厚度的影響。