基于非概率集合理論的屋面板風致疲勞壽命估計

孫大奇，朱 穎，劉曉光，雙 妙

(1. 中國鐵道科學研究院，北京 100081；2. 中國鐵道科學研究院集團有限公司鐵道建筑研究所，北京 100081；3. 高速鐵路軌道技術國家重點實驗室，北京 100081；4. 國核電力規劃設計研究院有限公司，北京 100095)

1976 年Morgan 和Beck[1]對澳大利亞達爾文地區的風災調查和實驗研究中指出，金屬屋面板的風致疲勞是Tracy 颶風造成損失的主要因素。然而，現有研究成果多集中于風荷載極值取值和結構在極值風荷載作用下的強度計算和變形校核，對疲勞損傷問題研究不足。由于屋蓋結構的氣動外形，來流在金屬屋面板上形成特征湍流，使結構在屋蓋邊緣受到很大的交變應力，忽視疲勞設計會造成嚴重的損失。

現有的結構疲勞分析方法大致可以分為時域方法和頻域方法，時域方法是從結構響應的應力時程出發，利用計數法直接提取結構響應的應力幅后，根據常幅S-N 曲線和變幅疲勞壽命預測的修正線性Miner 準則，對結構疲勞壽命進行估計[2]。而頻域方法是通過隨機振動理論由荷載的功率譜密度得到結構響應的應力功率譜密度，對于窄帶過程按單位時間內超越零界限的期望率估計疲勞壽命，對于寬帶過程則按極大值次數的期望值計算疲勞壽命[3]。

風致疲勞估計方法最初由Davenport[4]提出，建立在頻域疲勞分析方法的基礎上，假定結構在風載作用下的應力響應服從窄帶高斯分布，根據窄帶高斯過程的極值滿足瑞利分布，依據Wirsching的經驗公式[5]計算疲勞損傷，并假定平均風速滿足Weibull 分布進而得到結構的風致疲勞壽命[6]。

由于頻域疲勞分析方法的一些局限性，各國學者采用時域方法對金屬屋面板的風致疲勞問題進行研究。Xu[7]結合實測數據與風洞試驗數據，采用S-N 曲線與Miner 準則對屋面板氣動外形和特征湍流對疲勞壽命的影響進行了系統性的研究。Kumar 等[8]根據目標地區長期風環境和屋蓋疲勞實驗數據的特點，采用數值模擬的方法得到結構的風壓時程后，應用Miner 準則和Goodman方法對屋蓋結構的風致疲勞進行預測。

上述金屬屋面板風致疲勞研究中，各國學者多關注風荷載的隨機特性，忽略了金屬屋面板由于施工誤差或材料離散性引起結構本身的不確定性。結構的疲勞失效是受大量不確定因素影響的復雜過程，主要包括結構參數、外荷載和模型的不確定性[9]。考慮疲勞分析的復雜性，即使相同的荷載作用于相同的結構，結構疲勞壽命一般也不相同，且疲勞破壞通常會發生于結構最薄弱處，而材料間的個體差異和施工質量均會影響疲勞壽命。綜上所述，僅考慮荷載的隨機性而忽略結構的不確定性對結構疲勞壽命估計是偏于不安全的。

為考慮結構不確定性對疲勞損傷的影響，朱穎等[10-12]將結構不確定參數定義為區間變量，在寬帶頻域疲勞損傷的基礎上提出了疲勞損傷區間估計方法。在此基礎上，本文結合金屬屋面板表面風壓特性和工程所處地區風環境特性，在考慮結構參數不確定性的條件下，將區間分析方法引入時域疲勞損傷估計中，通過時域區間動力響應分析和疲勞損傷累積理論，得到金屬屋面板在脈動風荷載作用下的疲勞壽命區間。

1 問題描述

工程結構中通常采用概率模型定義結構自身由于安裝誤差、材料個體差異等因素引起的不確定性問題。在沒有足夠統計數據或合適概率模型的條件下，概率方法描述結構自身不確定性并不適合。同時，工程結構的不確定性通常是由于誤差或主觀認識不足造成，并不具有隨機特性。

對于金屬屋面板的疲勞損傷問題，由于受制造質量和安裝精度等因素的影響，疲勞壽命估計中僅能給出相關參數的區間范圍。這使得采用區間分析方法定義參數的不確定性，提供了一種解決金屬屋面板風致疲勞壽命估計問題中，考慮結構不確定性的新思路。

根據結構動力學和區間分析方法，考慮金屬屋面板結構整體矩陣M、C、K 隨不確定參數αj變化，屋面板在風荷載作用下的動力響應方程可表示為：

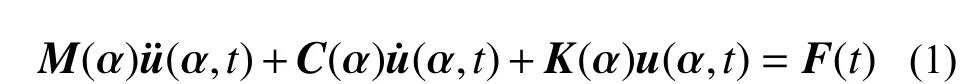
式中：M(α)、C(α)、K(α)分別為結構的質量矩陣、阻尼矩陣和剛度矩陣，均為不確定參數向量α 的函數；F(t)為結構的等效結點荷載，可分解為均值荷載μF和脈動荷載f(t)；應力均值區間按區間靜力方法計算[13]，并根據Goodman 公式修正；u(α,t)、u˙(α,t) 和u¨(α,t)分別為結構的節點位移、速度和加速度，均為不確定參數α 的函數。不失一般性，采用Rayleigh 阻尼模型定義金屬屋面板的阻尼矩陣，即：

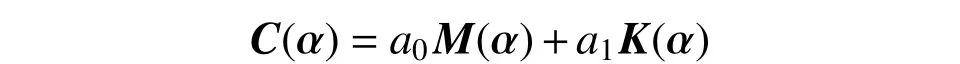
式中，a0和a1為Rayleigh 阻尼系數。

求解式(1)，并根據Mindlin 板殼理論，金屬屋面板任一點處的應力區間可表示為：

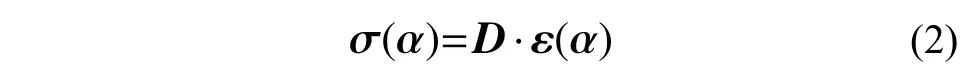
式中：σ(α) = [σf(α) σc(α)]T，σf(α)和σc(α)為彎曲應力和剪應力；ε(α) = [εf(α) εc(α)]T，εf(α)和εc(α)為彎曲應變和剪應變，分別表示為：

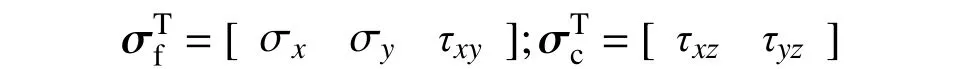
其中，彎曲應變和剪應變分別表示為：

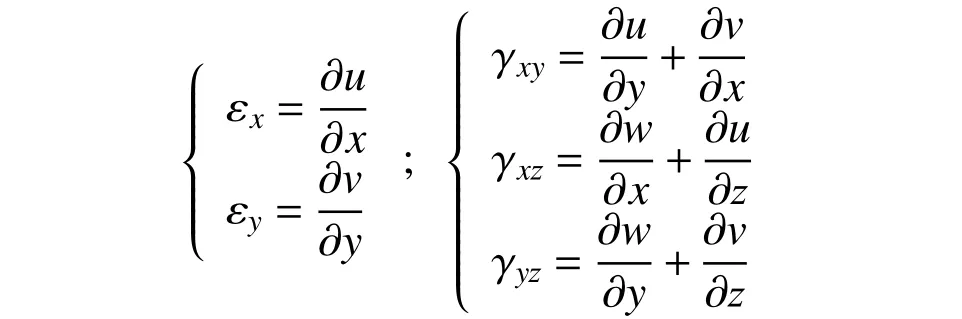
D = Trace[DfDc]，為彈性矩陣。其中：Trace[·]為矩陣的跡；Df和Dc為彎曲彈性矩陣和剪切彈性矩陣，分別表示為：

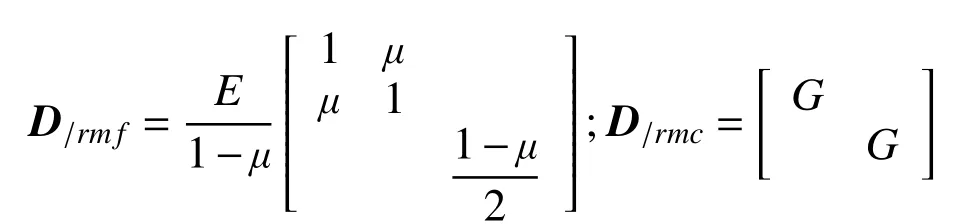
式中，μ和G 為泊松比和剪切模量。

金屬屋面板在脈動風荷載作用下的疲勞損傷是典型的多軸應力狀態下的疲勞問題。針對多軸應力狀態下的疲勞問題，需要確定等效多軸應力或者破壞臨界面上的正應力/切應力。本文采用Mises應力作為多軸應力下結構疲勞破壞的等效應力[14]，在平面應力狀態下，Mises 應力表示為：

式中：σ(α)=[σx(α) σy(α) τxy(α)]T；Q 為常數矩陣，表示為：

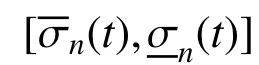
根據雨流計數法，金屬屋面板的疲勞損傷表示為：

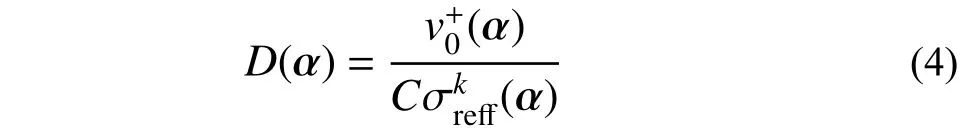
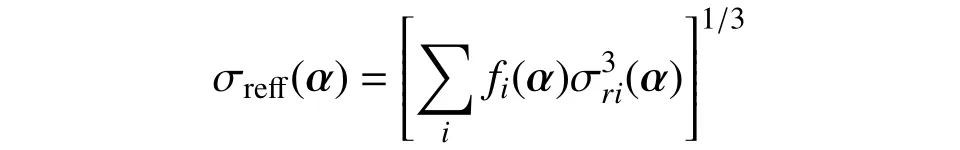
式中，fi(α)和σri(α)分別為等效應力的循環頻率和幅值。

與極值問題和頻域疲勞問題相同，考慮金屬屋面板參數不確定的時域疲勞壽命估計將轉化為計算不確定結構疲勞損傷或疲勞壽命的區間界限。根據線性損傷累積理論，金屬屋面板在風荷載作用下的疲勞壽命區間，表示為[10,15]：

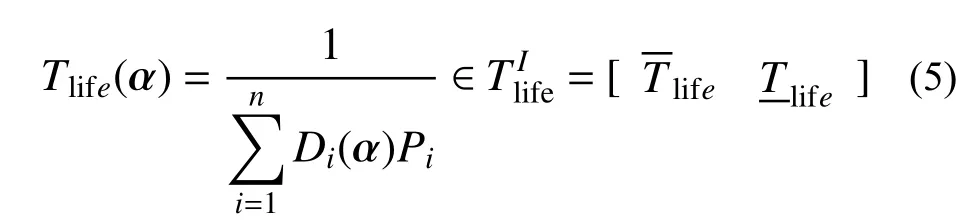
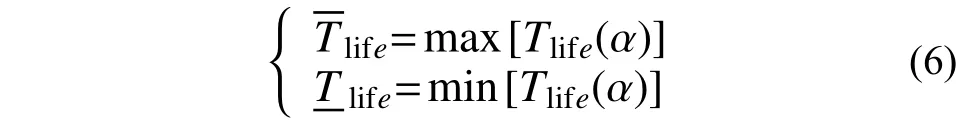
2 不確定結構區間動力響應

2.1 改進區間分析

Alefeld G 和Herzberger J[16]將基本運算、函數與實數區間相結合，提出區間分析理論用于解決實數有界區域的計算問題。為克服區間乘法運算過大的估計區間寬度、減小“依靠現象”的影響，在區間分析理論中引入單位對稱區間(Extra Unitary Interval, EUI)，則區間變量的名義值α0,i和半徑Δαi分別表示為[17]：

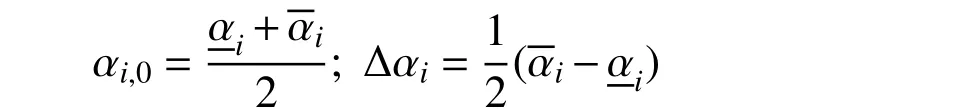
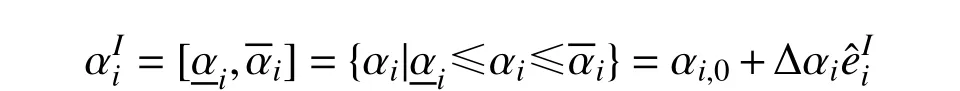
2.2 不確定結構的區間矩陣

根據攝動理論，當定義結構不確定參數αi是區間變量時，結構單元剛度矩陣可近似取一階Taylor 級數，表示為：

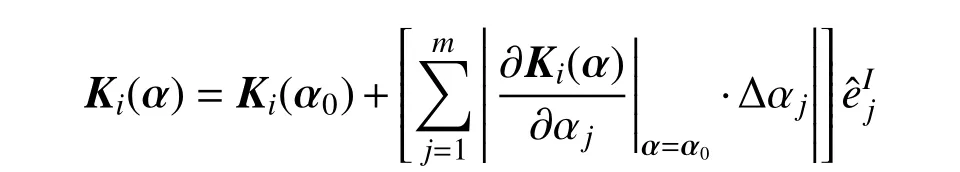
類似于有限單元法集成結構的整體矩陣，不確定的結構整體區間矩陣可表示為：

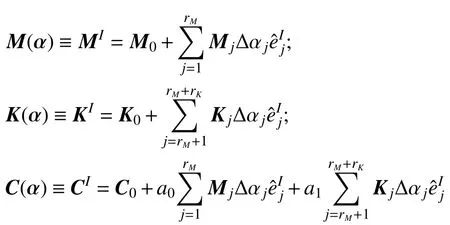
式中：rM和rK分別為質量和剛度矩陣的不確定變量數；M0、K0和C0分別為質量矩陣、剛度矩陣和阻尼矩陣的名義值；Mj和Kj為質量和剛度矩陣關于不確定參數αj的靈敏度矩陣，分別表示為：

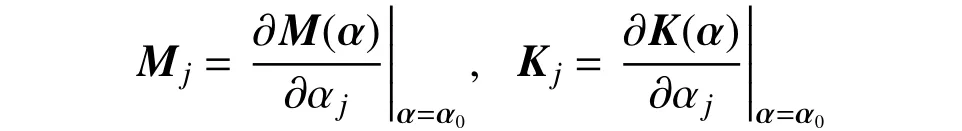
如果不確定參數ρj是結構矩陣的非線性函數，則需要將ρj等效為結構矩陣的線性函數αj。例如，桁架結構的桿件長度lj是不確定參數，對于結構的抗側剛度可將其等效為線性參數αj= 1/lj。

2.3 不確定結構區間動力學方程

根據非概率集合理論區間分析方法，不確定參數α 可以用區間向量表示。區間分析的動力響應問題，實質就是計算不確定結構在確定性荷載或隨機荷載作用下，結構響應的上界與下界。采用區間泰勒公式[18]，假設不確定參數為微小變化的參數，取一階泰勒公式，可得uI(α, t)的線性近似，表示為：

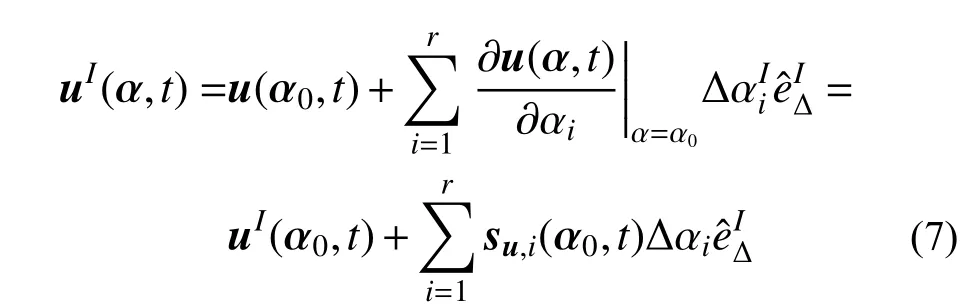
式中：u(α0, t)為結構的名義值響應向量；su,i(α0, t)為結構的一階靈敏度向量。這樣，結構動力響應的上界與下界就表示為：

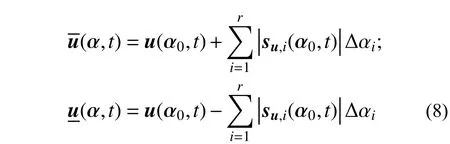
由式(8)可知，只需要知道結構動力響應的名義值u(α0, t)和不確定性參數αi的靈敏度su,i(α0, t)就可計算結構動力響應的區間[19]。

2.4 不確定結構區間動力響應分析

不失一般性假設結構阻尼為經典阻尼，根據振型分解法：

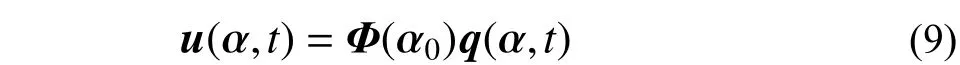
式中：Ф(α0)為n×m(m≤n)的矩陣，表示結構的前m 階振型；q(α, t)為結構的前m 階模態的振型坐標；Ф(α0)和q(α, t)可通過求解結構名義值的特征方程得到結構名義值的特征值和特征向量，將特征向量關于質量矩陣正則化，即：

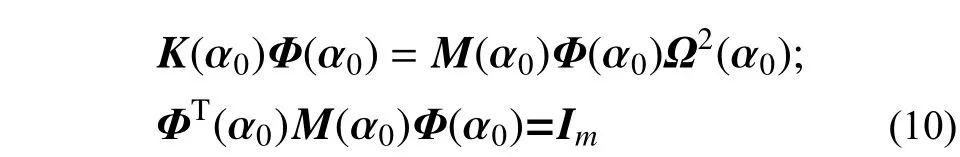
需要注意的是，式(9)是基于結構名義值的振型和頻率的特征方程，即假設結構名義值的剛度矩陣關于有界但不確定參數α 的變化范圍較小。

根據式(9)和式(10)，有界但不確定參數 αi的靈敏度可按振型分解方法表示為[20]：

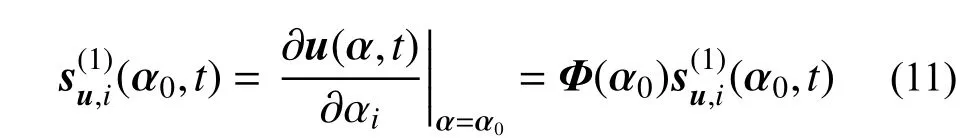
將式(9)代入式(1)，得關于振型坐標的二階常微分方程組，即：

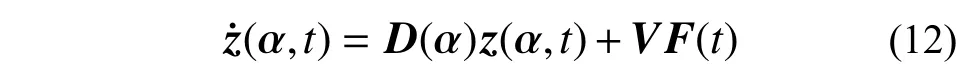
其中：

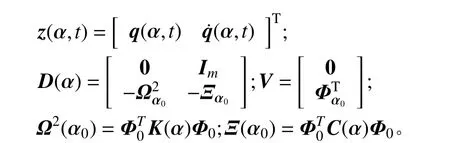
計算式(12)關于不確定參數αi的導數，并假定α = α0，則可得到關于有界但不確定參數αi靈敏度的二階常微分方程組，即：

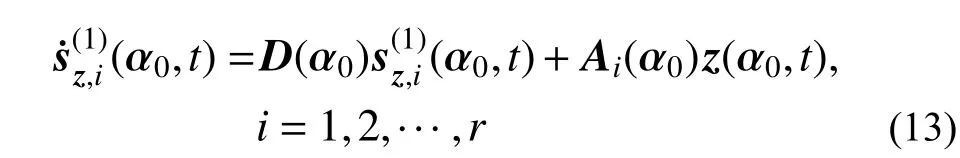
其中：

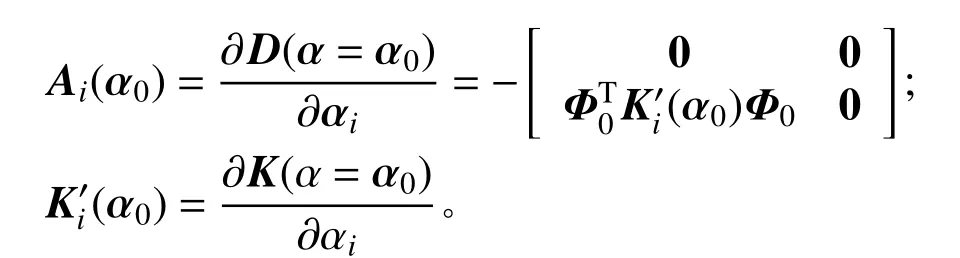
對于式(12)和式(13)可采用無條件穩定算法[21]計算結構的名義值和關于不確定參數的靈敏度值，即：

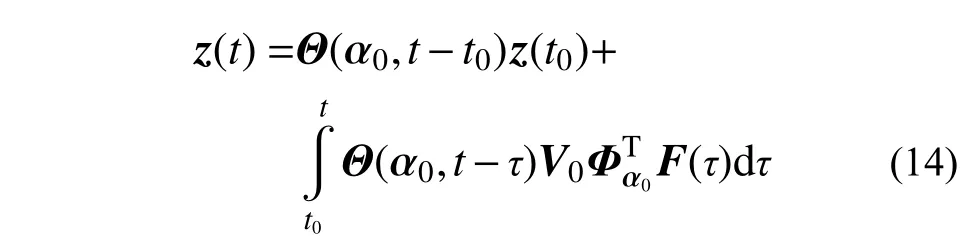
式中，V0為2m×m 矩陣，稱為布爾(Boolean)矩陣，表示為：

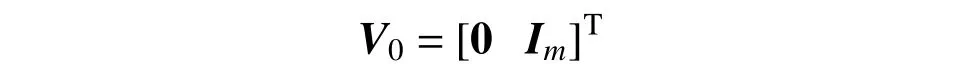
Θ(α0, t)稱為轉換矩陣，對于小阻尼結構可表示為[22]：

式中，h(t)和g(t)都是對角矩陣，其對角線元素表示為：

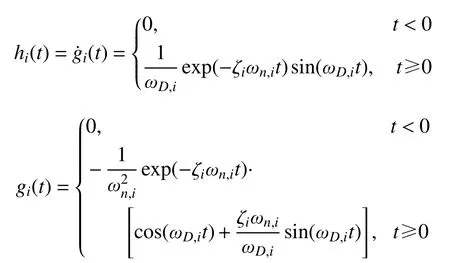
式中：ωn,i為無阻尼結構的第i 階圓頻率；ωD,i為有阻尼結構的第i 階圓頻率，ωD,i= (1-ζ2 i)1/2ωn,i。

通常情況下，式(14)中的卷積很難得到閉合解，需要通過數值方法計算。將外荷載在時間間隔(tk, tk+1]內分段線性插值，則每個時間間隔Δt內均滿足：

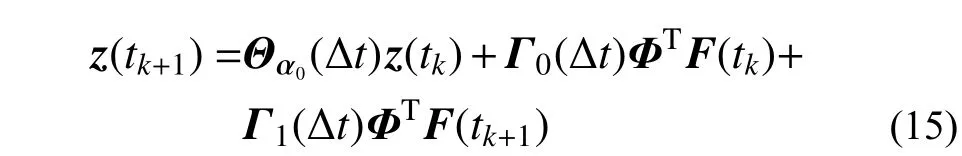
其中：

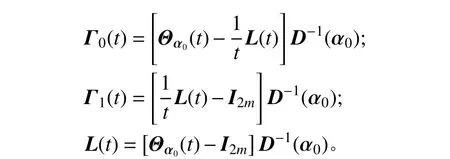
只需將式(14)的結構名義值響應z(α0, t)換成sz,i(α0, t)，類似的按照式(14)和式(15)即可得到不確定參數的靈敏度值。由z(α0, t)和sz,i(α0, t)按照式(8)和式(11)的振型疊加即可得到結構在動力荷載作用下響應的名義值和一階靈敏度，再按照式(8)即可得到結構的位移響應區間。

3 金屬屋面板疲勞壽命區間估計

將式(8)位移響應區間代入式(2)和式(3)中，得到考慮結構參數不確定條件時金屬屋面板在風荷載作用下的應力響應區間。根據式(4)和式(6)，金屬屋面板的風致疲勞損傷和壽命的上界和下界可表示為：

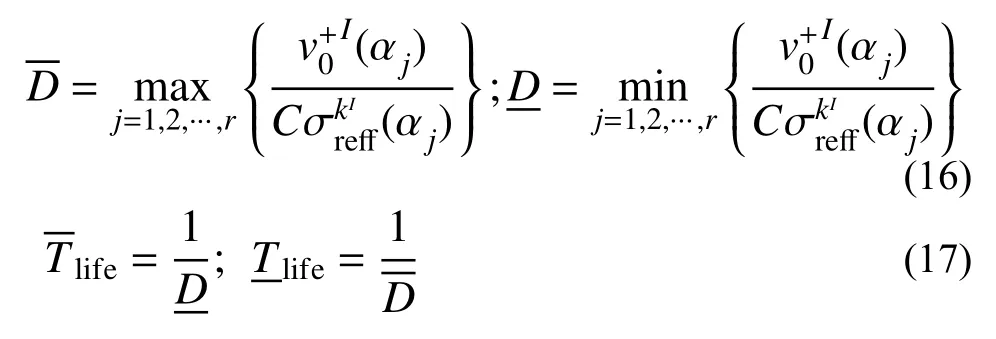
需要指出的是，如果待求解問題的不確定參數變量數為N 時，采用頂點法(vertex method)需要進行2N次動力響應分析和疲勞損傷估計。與頻域疲勞區間分析中的完全混合方法類似[11-12]，本文提出的考慮結構參數不確定條件下金屬屋面板風致疲勞損傷/壽命分析方法，僅需要一次動力響應分析即可計算金屬屋面板的疲勞損傷/壽命的界限，提高了結構疲勞損傷估計的計算效率。

4 脈動風荷載

如圖1 所示，金屬屋蓋結構的表面風荷載以風吸力為主，且靠近迎風面屋蓋前緣的風吸力較大，并向下游方向逐漸減弱。根據流動機理，通常將屋面分成分離區、再附區和尾流區三部分。由于分離區和再附區的風荷載表現明顯的非高斯特性，且風荷載數值遠大于尾流區。因此，為本文選用UWO 風洞實驗數據庫中分離區和再附區實測風壓系數譜作為風荷載目標譜。通過諧波疊加法和非高斯穿越過程[23]，模擬生成金屬屋面板表面非高斯壓力系數，則金屬屋面板表面風壓與風壓系數、平均風速可表示為：

式中：Cp(t)為壓力系數；Umean為平均風速；ρ 為空氣密度。

圖 1 大跨屋蓋結構表面特征湍流Fig.1 Turbulent characteristics of large-span roof structures

圖 2 模擬的非高斯風壓系數時程圖Fig.2 Simulated non-Gaussian time histories of wind pressure coefficients

圖2 所示為由金屬屋面板不同位置處壓力系數功率譜密度按諧波疊加法和非高斯穿越過程模擬的非高斯壓力系數和概率密度函數。為消去動力響應的初始狀態，時程長度為630 s，并從30 s后對結構的疲勞損傷進行分析。圖2 中概率密度柱狀圖中實線表示目標風壓系數的概率密度函數，虛線表示與模擬風壓系數相同均值和方差的高斯過程的概率密度函數。如圖2 所示，模擬壓力系數與目標壓力系數的具有相同概率分布，表現出明顯的非高斯特性。需要說明的是，角部分離區的偏斜系數和峰態系數分別是-0.79 和4.2，屋脊分離區的偏斜系數和峰態系數分別是-0.72和3.8，角部再附區的偏斜系數和峰態系數分別是-0.92 和4.97，屋脊再附區的偏斜系數和峰態系數分別是-0.74 和3.98。圖3 比較了目標譜與風壓系數時程的模擬譜，結果表明不同位置處壓力系數功率譜密度較好的吻合了目標譜。

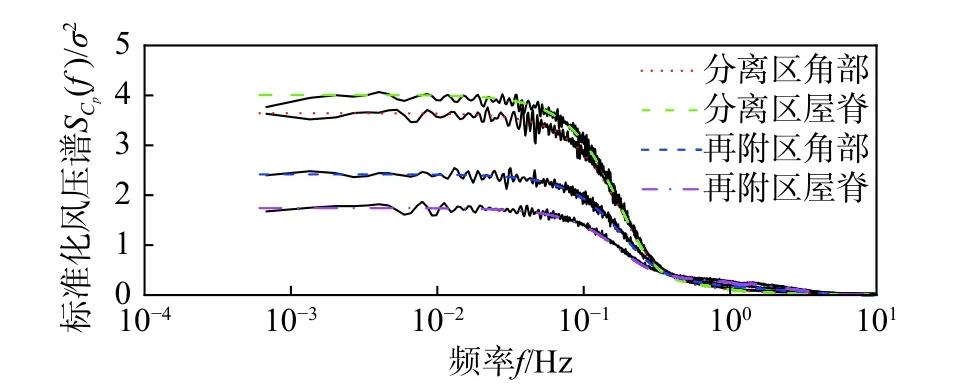
圖 3 模擬的非高斯時程功率譜與目標譜比較Fig.3 Comparison of target spectrum and PSDs of simulated non-Gaussian time histories

將平均風速從1 m/s～21 m/s 范圍內，每隔2 m/s為一個風速單元，計算該風速單元內的疲勞損傷，并考慮平均風速的概率密度函數，根據式(16)和式(17)得到給定平均風速考慮金屬屋面板結構參數不確定條件下的疲勞損傷和疲勞壽命區間。

圖4 所示為采用能量密度法[24]，根據北京氣象塔實測風速數據[25]，統計得到北京地區城市地貌年平均風速兩參數Weibull 分布。如圖所示，采用能量密度法準確得到平均風速的概率密度函數，并以該平均風速概率密度函數作為本文計算金屬屋蓋風致疲勞的平均風速概率密度函數。

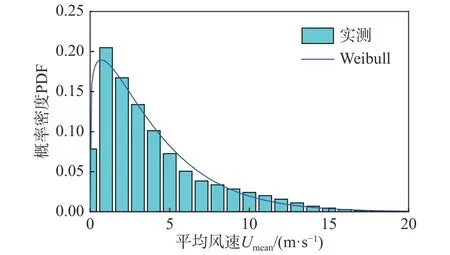
圖 4 實測數據[21]與Weibull 平均風速模型對比Fig.4 Comparison of probability density of mean wind speed by Weibull distribution and measured data

5 算例

本文數值算例均采用Matlab R2014a 程序編寫，結構整體矩陣及驗證參見文獻[26 - 27]。圖5為考慮參數不確定金屬屋面板在風荷載作用下疲勞損傷/壽命的計算程序流程圖，可按步驟編寫計算程序。

圖 5 金屬屋面板疲勞損傷區間分析方法計算程序流程圖Fig.5 Flow-chart of interval analysis method of time domain fatigue evaluation

將本文所述區間疲勞分析理論應用于金屬屋面板風致疲勞計算中，材料參數和屋面板尺寸均按照《壓型金屬板工程應用技術規范》[28]中鋁合金材料取值，彈性模量、泊松比、板厚和密度分別為7.0×1010Pa、0.3、0.6 mm 和2.7×103kg/m3；采用四邊形單元建模，取0.8 m×4.0 m 大小屋面板[27]，短邊固支、長邊簡支，屋面板在x 方向、y 方向上分別均分20 和4 等分，共劃分80 個單元，如圖6所示；鋁合金材料的S-N 曲線通過常規軸向拉伸試驗方法獲得[29]：

式中：N 為發生疲勞破壞時循環荷載的次數；S/MPa 為應力幅。

圖 6 屋面板幾何尺寸和計算點示意圖 /mm Fig.6 Geometry size and calculation point

考慮彈性模量和板厚是結構不確定參數兩種不同情況，且不確定性大小分別為5%、10%和20%。將不同區域風荷載分別作用于金屬屋面板，通過根據式(8)分析計算得到屋面板響應撓度的區間時程，由式(2)和式(3)得到應力響應。

圖7 分別表示考慮5%板厚不確定情況下，金屬屋面板分離區角部、分離區屋脊和再附區角部、再附區屋脊在脈動風荷載作用下的金屬屋面板中心位置的Mise 等效應力響應。右側直方圖表示名義應力的概率密度，點線和實線分別表示應力上界和下界的概率密度。如圖所示，如果僅按結構名義值進行計算將會過高估計結構的實際情況，不能滿足結構設計要求。需要強調的是，本文采用的區間動力響應分析方法僅需一次動力響應分析就可得到參數不確定結構的動力響應區間，而頂點法需要對不確定參數進行組合后，再進行動力響應分析，并從計算結果中選取動力分析的極大值和極小值。就本例而言，當定義金屬屋面板的板厚為不確定參數，且不同單元的板厚不相關，采用頂點法需要通過280動力響應分析才能得到金屬屋面板在脈動風荷載作用下的動力響應區間，而本文方法僅需一次動力響應分析，大幅減少了計算量。

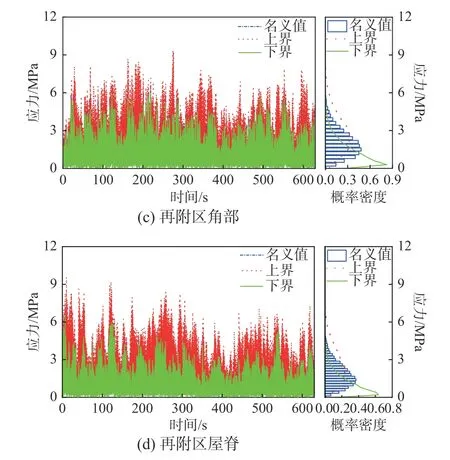
圖 7 5%板厚不確定情況下屋面板的動力響應時程Fig.7 Dynamic response time history analysis under 5%uncertainty of elastic modulus

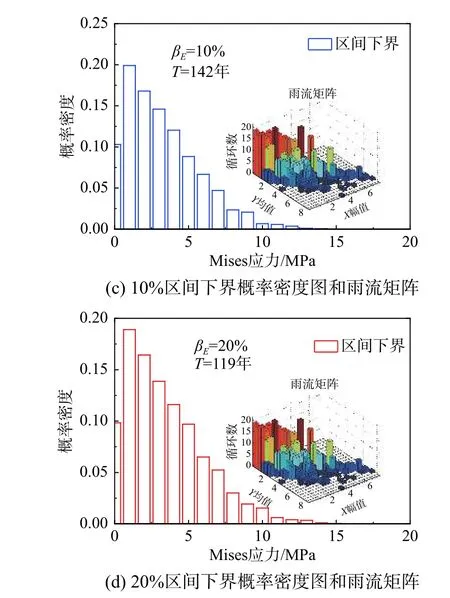
圖 8 疲勞壽命關于彈性模量靈敏度分析Fig.8 Comparison of fatigue life by sensitivity of elastic modulus

圖8 和圖9 分別是定義彈性模量和屋面板厚度是不確定參數情況下，采用式(17)計算得到屋面板分離區角部中心處的疲勞壽命下界。當不考慮結構不確定時，分離區角部屋面板的疲勞壽命為159 年。考慮金屬屋面板由于施工等因素引起彈性模量或板厚在一定范圍內不確定時，屋面板的疲勞壽命隨結構參數的不確定區間增大而降低；當金屬屋面板材料的彈性模量和板厚在20%范圍內不確定時，屋面板中心處的疲勞壽命分別下降至119 和22 年。需要說明的是，受安裝誤差、溫度等引起的內力重分布等因素影響，結構在施工和實際使用過程中情況將更為復雜。

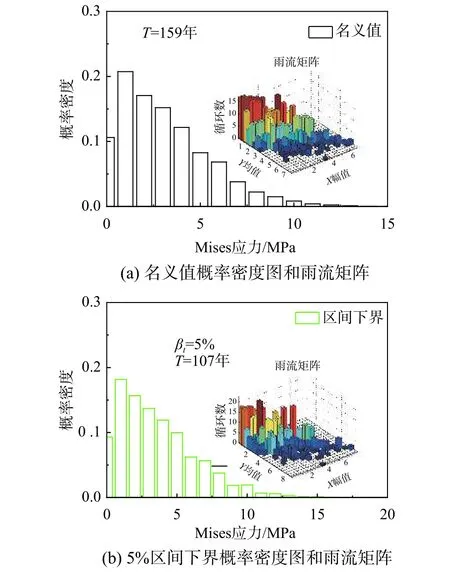
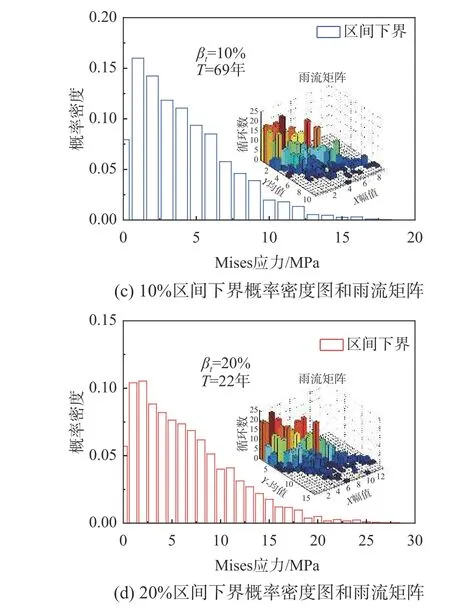
圖 9 疲勞壽命關于板厚靈敏度分析Fig.9 Comparison of fatigue life by sensitivity of thickness

圖10 通過調節式(8)中單位對稱區間，比較了彈性模量和板厚的不確定性對金屬屋面板風致疲勞壽命的影響。由于材料的S-N 曲線是高次非線性方程，因此金屬屋面板的疲勞壽命區間下界隨彈性模量和屋面板板厚降低而降低。同時，屋面板的彎曲剛度與板厚是三次立方關系，屋面板板厚的不確定性對屋蓋結構的疲勞壽命有較大影響。需要強調的是，本文方法僅通過一次動力響應分析即可計算結構的疲勞損傷/壽命的界限，大幅減少了計算量。

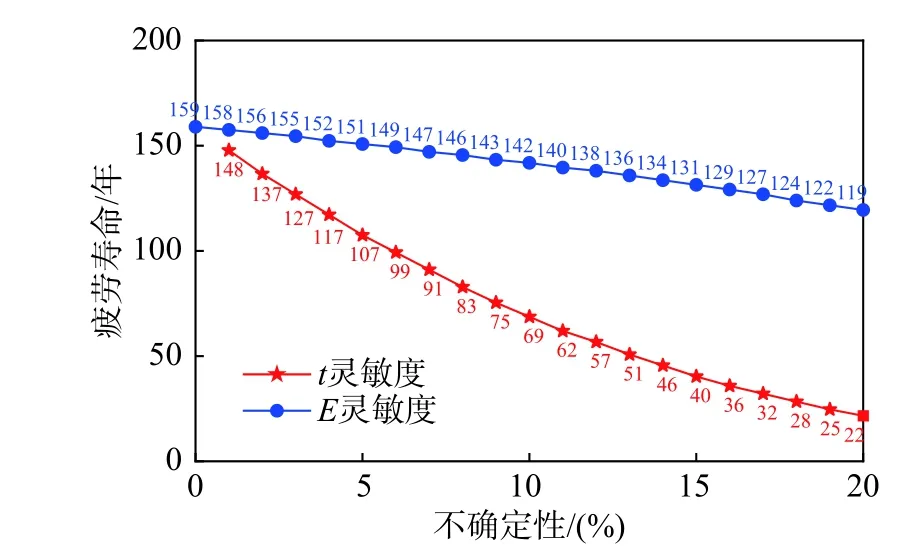
圖 10 疲勞壽命關于彈性模量和板厚靈敏度分析Fig.10 Comparison of fatigue life by sensitivity of elastic modulus and thickness

6 結論

在時域疲勞分析方法的基礎上，采用區間參數模型定義結構參數的不確定性，提出考慮由于施工誤差等因素引起的結構不確定條件下金屬屋面板在脈動風荷載作用下的疲勞損傷/壽命估計方法。本文方法具有以下特點：

(1) 在時域疲勞分析方法的基礎上，采用區間參數模型定義金屬屋面板的不確定參數，考慮施工誤差等因素對屋面板疲勞損傷/壽命的影響；

(2) 在疲勞損傷估計中對不確定參數進行組合，僅需一次動力響應分析即可計算金屬屋面板的疲勞損傷/壽命的界限，避免了頂點法需要多次動力響應分析；

(3) 與頻域疲勞區間分析方法相同，可通過調節不確定參數的單位對稱區間，實現同一參數不同不確定半徑疲勞損傷/壽命的近似計算。

數值算例表明：如果考慮結構不確定性，則結構的疲勞壽命率將大幅降低；因此對于重要結構，需要在疲勞分析中考慮結構的不確定性。同時，與傳統的確定性方法和概率方法不同，區間理論得出的并不是結構疲勞壽命的準確值，而是根據結構的不確定性大小給出合理的疲勞壽命區間，當結構到達疲勞壽命區間下界時，結構就有可能發生疲勞破壞，需要及時對結構采取檢修或加固等維護措施。