選舉中的算法問題

大多數人的記憶中都會有上小學時選班長的情景，再后來，我們也經歷過許多不同的選舉過程。如何設計公平合理的選舉規則是遠遠超出了數學和算法范疇的復雜問題。本文只討論在特定規則下如何獲得選舉結果的相關的算法。

一群人按照一人一票的方式（每張選票具有相同權重）在（通常數量很少的）候選人中選出一位“勝出者”（如班長），最簡單的規則就是票數最多者當選（假設沒有并列）。在沒有電子手段之前，最流行的做法就是投票完成后，將候選人名字列在黑板上，隨著“唱票”進程，在候選人名字后畫“正”字。最后數出每人得票數，即可知誰是當選者。

模擬“畫正字”的計票方式

如果候選人人數k不大，可以定義k個元素的數組candidates，其中candidates[i]是整數，表示候選人i的得票數，i=0，1，…，k-1。若投票人數為n（通常n>>k），長度為n的整數序列vote_sequence可以看作所有選票的集合（次序無意義），其中，不在上述i定義范圍內的項為無效選票。圖1所示是模擬計票的過程。

得到計票值后，數組candidates中的最大值對應的候選人即“勝出者”，如果對candidates排序，則可以得到所有候選人得票數的遞增或遞減序列。在本專欄我們曾討論過排序問題[1]（文章刊登于本刊2020年第7期），知道基于key比較的排序算法在最壞情況下最優解的復雜度下限為nlogn。但這里是對candidates（大小為k）排序，而不是對vote_sequence（大小是n）排序，因此可以說復雜度為O（klogk）。另一方面，鑒于在大多數表決類應用場景下，k值遠小于n，甚至可以認為與n的大小沒有關系，即可看作是常量，也可以從vote_sequence的角度來看這排序過程。也就是想象有若干一字排開的“桶”，數量相對于n很小，例如有一個與n無關的常數上界c。一次性順序掃描vote_sequence，每個元素嘗試依次與每個桶中的一個元素相比，發現相同就扔進去（其實就是計一次數），發現兩次相繼的比較為一大一小，就啟用一個新桶插在中間，將元素扔進去。當然，兩端的情況稍有點特殊。這樣一來，掃描全部完成后就得到了最多c個依元素大小序排列的桶，依次輸出桶中元素的個數，就得到了相當于是cadidates的排序。由于在一次性掃描vote_sequence過程中每個元素最多需要c次比較，與n無關，因此這里的排序代價也可以看作O（n）。

基于“眾數”的選舉規則

采用“簡單多數”規則，當候選人數大于2時當選者未必能得到多數人的支持。為了避免這一缺憾，另一種常用的選舉規則要求當選者得到的選票數必須大于投票者總數的一半（有些選舉可能規定達到半數即可，本文后面的討論要求當選者得票數必須大于半數）。

不妨假設所有選票均為有效選票，選票上給出投票人選擇的候選人序號（非負整數），所有選票可以表示為一個有限長度的輸入序列。如果該序列中存在某個數值，出現次數大于序列長度的一半，則該數值稱為序列中的“眾數”。我們注意到，“眾數”一詞在統計學中不一定非得超過半數。這里借用此名詞，在本文范圍內一定是指出現次數大于總項數的一半。因此，如果眾數存在，顯然只有一個。

我們可以將基于“眾數”規則選舉的計票過程抽象為：對于任意輸入的有限長度序列，找出該序列中的眾數，或者判定眾數不存在。如果輸入表示全部選票，則如果眾數存在，問題的解即當選者，反之，若判定眾數不存在，則確定“無當選者”。

眾數判定問題表述簡單，也挺有趣。可能因為它較少出現在流行的算法教科書中，不時會被一些IT技術企業選擇作為招聘面試題。面試者最容易想到的算法就是排序。一旦將輸入序列排序，下面的兩種方法均可得到需要的結果：

（1）計數：掃描已排序的序列，可以依次統計出每個數值出現的次數。根據最大出現次數即可判定眾數或者判定眾數不存在。

（2）中值：在已排序的序列中讀出第n/2」項（n為序列長度）。對于按從小到大排序的序列，這是“中位數”。如果從該項起直到序列末尾的數值均相等，則該數值即為“眾數”，否則序列中不存在眾數。

排序的代價是O（nlogn），對于這里的解題目標而言，似乎代價大了些。讀者可能會看出，如果我們知道了中位數，不需要排序，只要掃描序列，統計中位數出現的次數就能得到需要的結果。因為序列中有眾數當且僅當中位數即眾數（為什么？）在大多數算法教科書中能找到計算中位數的線性代價算法，這里不再贅述。

下面介紹一個非常巧妙的眾數算法，不需要排序，而且比求中位數更簡單。[2]

如果長度為n的序列中確實存在眾數c，其出現次數為t。如果從序列中刪除兩個不相等的元素，則剩下的序列中c仍然是眾數。被刪除的兩項不相等，其中最多有一個是c，因此余下的序列長度為n-2，而包含的c至少為t-1個。根據眾數定義t>n/2，則t-1>n/2-1=（n-2）/2。

其實，對任一“候選值”，通過統計判定其是否眾數很容易，代價是線性的。問題是如何找“候選值“，根據上述分析，刪除不相等的兩項，不會將可能存在的“候選者”漏掉，換句話說，當這一過程一直繼續，到剩下的序列中只含一個值時（也可能不是一項），這個值即候選值。它未必是眾數，但只要掃描一次原序列進行統計即可判定。

算法包含兩個部分，首先是希望篩選出候選值，然后是統計候選值出現次數是否大于序列總長度的一半。算法過程如上頁圖2所示。

很顯然，算法兩個階段代價均為O（n），因此總代價是線性的。這個算法在整個過程中完全不涉及未當選者得票數的相關數據，這對于算法的人性化而言（保護未當選者隱私）是很好的性質。

要求投票人給出更多傾向性信息的選舉

上述選舉規則非常簡單，每張選票只需要給出投票人中意的一個候選人。但當候選人數大于2時，很難保證有眾數存在，很常見的情況是得票數比較分散，要確保勝出者得票超過一半（甚至三分之二），有時需要多輪投票。

如何使選舉過程既能有效操作，同時也讓選舉結果更容易被接受，促進社會和諧，需要設計更復雜的選舉過程。相關理論與分析已經成為數學在社會科學中應用的一個重要方面。[3]本文只通過一個例子討論要求投票者提供更多意向信息的選舉規則。

某班級要推選出一人參加學校的演講比賽，共有6名同學報名（用A、B、C、D、E、F表示）。全班同學需要投票選出一人代表班級參賽。為了避免選票過于分散，難以確定勝出者，可以考慮以下兩種方案：

（1）每張選票不是只填寫一個候選人的名字，而是按照投票者意向強弱對6名候選人排序。

（2）組織候選人進行一對一預選對抗賽，每位投票人（假設總數為奇數）對每組對抗者選定贊同者，按照多數原則決定二者之間的勝負，然后將所有預選賽的結果匯總，作為推舉最終代表的基礎數據。

前者是實踐中經常采用的方法，一般會將每位投票人給出的序號作為“得分”，累加后分值最小者當選。（當然也不能排除得分相等）

后者似乎很少在實際選舉中使用。但是讀者很容易想到，體育比賽經常采用這樣的方法（循環賽）確定冠軍（“勝出者”）。原因是許多體育比賽項目一對一對抗結果往往有客觀標準。其實第一種選舉方案的選票包含了第二種方案能提供的信息（任何兩個候選人，排序前者優于排序后者），但從第二種方案得到的信息確定勝出者仍然不是很容易的。下面，我們考慮如何從一對一對抗結果導出“名次”，包括第一名（“當選者”）。討論采用體育循環賽的表示方式，在這個語境下介紹相關算法。當排名次問題解決了，決定選舉勝出者的問題自然也解決了。

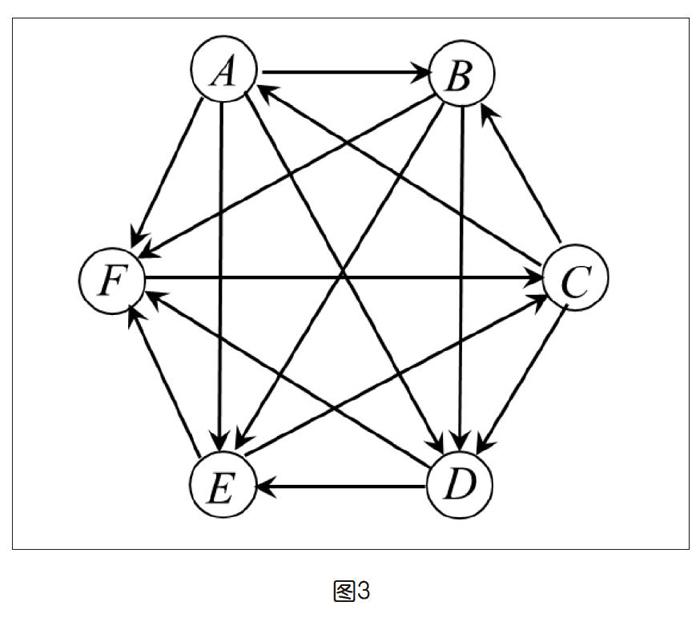
假設6名候選人一對一對抗結果對每張選票采用簡單多數匯總如圖3所示，圖中的有向邊uv表示候選人u在一對一對抗中勝候選人v。

這樣的有向圖稱為“競賽圖”。如果不考慮邊的方向，這是完全圖，因此它能夠完整準確地描述沒有平局的“循環賽”的結果。從循環賽所有場次的勝負關系怎樣才能合理地給出全部參賽者的名次呢？比較自然的想法是按照勝場多少排序。由圖3可以得到表1。

可以看到，勝出者是A。不過C可能會抱怨：雖然比A少了一個勝場，但擊敗的對手看上去比較強，而且還擊敗了排名第一的A。現實生活中很少有采用循環制的體育比賽結果沒有人“吐槽”的。盡管不可能有讓所有人都滿意的方法，但如果能在簡單地數勝出場次之上，多少也考慮對手強弱的因素，結果的可接受度應該會更好些。

為了能體現勝出場次對手的強弱差異，可以定義得分向量sk=（Ak，Bk，Ck，Dk，Ek，Fk），其初始值（k=0）各分量值設定為1，sk+1各分量的值等于sk中該選手擊敗的各選手對應值之和。按照這一規則，計算前幾個sk的值如下頁表2所示（諸分量對應于A，B，C，D，E，F）。

從表2中可看出，s4到s5各選手的排序沒有變化。只要輸入數據對應的有向圖是強連通的，且選手人數不小于4，可以證明得分向量的值一定會收斂到一個固定次序，這就可作為排名。我們略去數學細節，只給出計算選手名次的算法，如果針對的是前面提到的選舉問題，則排名第一的為當選者。

首先給出所需數據的定義：

player：選手名列表，輸入，在整個算法過程中不改變。

winning：每個選手戰勝的對手列表，這是一個二維表，為了方便處理，即使無勝局的選手在列表中也有相應的項（空表）。上述例子中winning=[[B，D，E，F]，[D，E，F]，[A，B，D]，[E，F]，[C，F]，[C]]。winning相當于輸入的競賽圖，在整個算法過程中不改變。

score：得分向量，算法過程中更新，即上述的sk。注意：得分向量中每個分量對于選手的次序始終是列表player的次序，改變的只是分值。

ranking：選手排名列表，在上述例子中初始值為[A，B，C，D，E，F]，score每輪更新后做一次排序。注意：每輪排序依據的關鍵字是score中的相應項，與ranking本身諸項值（選手名）無關。

還需要定義下列函數：

score_update：按照上文介紹的規則，更新得分向量的值。

player_sort：根據得分向量各項值，對ranking中的選手名按照分值從大到小排序。此函數為布爾函數，如果本輪并未發生元素置換，返回false，否則返回true。在待排序對象很小時，效率不是問題，采用最簡單的“冒泡”算法即可。

player_number：此函數將選手名轉換為該選手在列表player中的下標值。

算法過程表述如上頁圖4所示。算法描述中按照本文例子的情況是6名選手，只要稍作修改便可以適用于不同的輸入。

參考文獻：

[1]陳道蓄.排序問題[J].中國信息技術教育，2020（07）：24-27.

[2]Udi Manber.算法引論：一種創造性方法（中文版）[M].北京：電子工業出版社，2010.

[3]Wallis，W.D..Mathematics of Elections and Voting[M]. Berlin：Springer， 2014.

注：作者系南京大學軟件學院原院長，計算機系原系主任。