直流電壓降方法在鋼材疲勞過載延遲效應(yīng)研究中的應(yīng)用

夏昊陽，吳 昊

(同濟(jì)大學(xué)航空航天與力學(xué)學(xué)院，上海 200092)

0 引 言

疲勞斷裂是鋼材常見的失效或破壞形式之一，因?yàn)榻饘俳Y(jié)構(gòu)件尤其是鋼材在實(shí)際使用中，常常承受著變幅載荷。已有研究[1]發(fā)現(xiàn)，過載會(huì)導(dǎo)致裂紋擴(kuò)展的延遲，而預(yù)測變幅加載下的裂紋擴(kuò)展速率是非常具有挑戰(zhàn)性的一項(xiàng)工作。Paris公式是預(yù)測宏觀裂紋擴(kuò)展速率最常用的方法之一，該模型假設(shè)裂紋擴(kuò)展速率由應(yīng)力強(qiáng)度因子幅值ΔK決定[2]；但是基于線彈性斷裂力學(xué)的Paris公式無法準(zhǔn)確描述過載延遲效應(yīng)。近年來有非常多的學(xué)者對(duì)鋼材的疲勞過載延遲現(xiàn)象進(jìn)行了研究。根據(jù)裂紋閉合現(xiàn)象，WOLF[3]定義了閉合率U并給出了過載后的模型公式；為了反映延遲效應(yīng)，WILLENBORG等[4]提出用延遲系數(shù)Cp來預(yù)測過載后的裂紋擴(kuò)展速率；BACILA等[5]通過分段線性函數(shù)方法對(duì)Willenborg模型進(jìn)行了修正；WU等[6]使用權(quán)函數(shù)方法來量化殘余應(yīng)力強(qiáng)度因子并計(jì)算殘余應(yīng)力引起的裂紋閉合效應(yīng)，同時(shí)提出了適用于一些標(biāo)準(zhǔn)試樣的殘余應(yīng)力強(qiáng)度因子的計(jì)算公式[7]；DAI等[8]提出了一種以塑性修正后的應(yīng)力強(qiáng)度因子為新的驅(qū)動(dòng)力來預(yù)測裂紋擴(kuò)展速率的方法；YUEN等[9]從裂尖塑性區(qū)出發(fā)，考慮了材料特性對(duì)擴(kuò)展行為的影響后提出了一個(gè)改進(jìn)的Wheeler模型；HARMAIN[10]利用裂紋閉合與裂尖塑性區(qū)的耦合效果來解釋單峰過載延遲現(xiàn)象，并給出了對(duì)應(yīng)的計(jì)算公式。但是，上述方法都需要針對(duì)不同材料進(jìn)行試驗(yàn)以獲取參數(shù)進(jìn)行擬合，應(yīng)用限制非常大。

由于疲勞裂紋的測量通常在惡劣的動(dòng)態(tài)環(huán)境中進(jìn)行，因此應(yīng)用一個(gè)好的疲勞裂紋檢測方法是非常必要的。其中，直流電壓降(Direct Current Potential Drop，DCPD)方法[11-12]是一種基于材料導(dǎo)電性能的疲勞裂紋檢測方法，該方法的優(yōu)點(diǎn)包括：可克服環(huán)境對(duì)測量過程的影響，即使在高溫易腐蝕等惡劣環(huán)境中也可進(jìn)行測量；可通過溫度補(bǔ)償來消除溫度引起的誤差；對(duì)噪聲干擾不敏感；測量時(shí)通過改變直流電的方向測量2次即可消除金屬與導(dǎo)線的接觸電壓；可測量小裂紋的萌生速率和裂紋擴(kuò)展速率，具有較高的精度。因此，DCPD方法非常適合于具有良好導(dǎo)電性能的鋼材的疲勞裂紋研究。當(dāng)恒定直流電流穿過試樣裂紋區(qū)域，裂紋長度的變化會(huì)改變這段區(qū)間的電阻，從而改變2個(gè)探頭之間的電勢差，因此DCPD方法通過測量裂紋兩側(cè)直流電勢差來反映裂紋實(shí)時(shí)長度，進(jìn)而得到裂紋擴(kuò)展速率。目前，有關(guān)DCPD方法在鋼材疲勞過載延遲效應(yīng)研究中的應(yīng)用報(bào)道較少。作者通過引入等效殘余應(yīng)力強(qiáng)度因子ΔKres，提出了一種無材料擬合參數(shù)的新型驅(qū)動(dòng)力模型，基于有限元標(biāo)定輔助DCPD方法，采用過載疲勞試驗(yàn)對(duì)4種不同鋼材過載后的裂紋擴(kuò)展速率與延遲疲勞壽命進(jìn)行測試，驗(yàn)證了預(yù)測模型的準(zhǔn)確性。

1 新型驅(qū)動(dòng)力模型的建立

在線彈性斷裂力學(xué)中，裂尖拉伸應(yīng)力σy的計(jì)算公式為

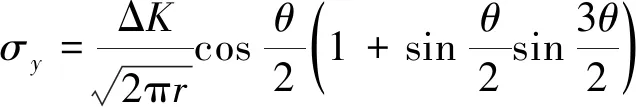
(1)

式中：r，θ為極坐標(biāo)參數(shù)。

Rice在此基礎(chǔ)上提出并應(yīng)用塑性疊加法來計(jì)算殘余應(yīng)力[13]，即在卸載過程中，基于Bauschinger效應(yīng)，反向屈服強(qiáng)度為2σ0(σ0為屈服強(qiáng)度)，疊加后的殘余應(yīng)力σres分布可由圖1得到，圖中Δσ為加載與卸載時(shí)所施加的力，x為裂紋擴(kuò)展方向的長度。

圖1 考慮塑性區(qū)應(yīng)力分布的塑性疊加法原理Fig.1 Principle of plastic stress superposition considering stress distribution in plastic zone: (a) stress distribution curve after loading;(b) stress distribution curve after unloading and (c) stress distribution curve after superposition

基于權(quán)函數(shù)[6]提出的等效殘余應(yīng)力res計(jì)算公式為

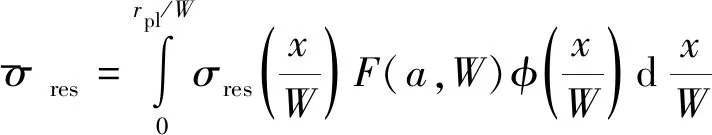
(2)

式中：W為試樣寬度；a為裂紋長度；rpl為塑性區(qū)半徑；x為沿裂紋擴(kuò)展方向坐標(biāo)；F(a,W)為權(quán)函數(shù)幾何函數(shù)；φ(x/W)為與試樣幾何尺寸有關(guān)的權(quán)函數(shù)，該函數(shù)為單調(diào)遞減的正函數(shù)，且當(dāng)x=0時(shí)，φ(0)=1[14]。

根據(jù)權(quán)函數(shù)要求，用滿足要求的負(fù)指數(shù)函數(shù)作為權(quán)函數(shù)φ(x/W)，得到：

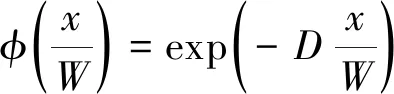
(3)

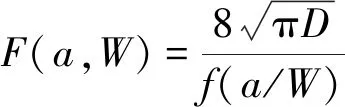
(4)

式中：D為與試樣類型和尺寸有關(guān)的無量綱擬合參數(shù)，對(duì)于緊湊拉伸(CT)試樣，由試驗(yàn)結(jié)果擬合得到的D取30；f為CT試樣的無量綱幾何函數(shù)[15]。

將得到的φ(x/W)，F(xiàn)(a,W)代入式(2)，即可得到等效殘余應(yīng)力。等效殘余應(yīng)力強(qiáng)度因子ΔKres的計(jì)算公式為

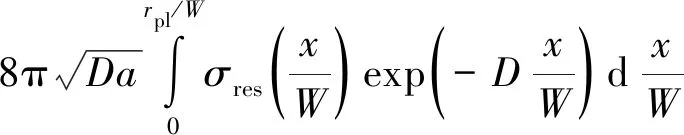
(5)

有效應(yīng)力強(qiáng)度因子ΔKeff為應(yīng)力強(qiáng)度因子幅值ΔK減去等效殘余應(yīng)力強(qiáng)度因子ΔKres，即

ΔKeff=ΔK-ΔKres

(6)

為了量化單峰過載后塑性區(qū)對(duì)疲勞壽命的影響，將ΔKeff代入Paris公式來預(yù)測裂紋擴(kuò)展速率和延遲疲勞壽命，計(jì)算公式為

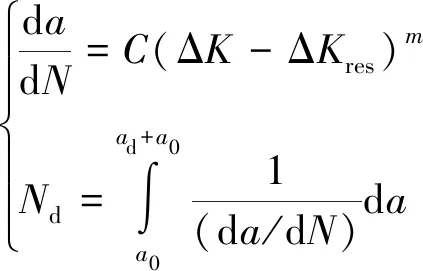
(7)

式中：C,m為Paris公式參數(shù)；a為裂紋長度；N為循環(huán)次數(shù)；da/dN為裂紋擴(kuò)展速率；Nd為延遲壽命；a0為初始裂紋長度；ad為裂紋擴(kuò)展長度。

2 試樣制備與試驗(yàn)方法

采用DCPD方法對(duì)4種鋼材的CT試樣進(jìn)行過載疲勞試驗(yàn)以驗(yàn)證預(yù)測模型的通用性，這4種鋼分別為2種不同熱處理態(tài)12NiCr6鎳鉻鋼、1080高碳鋼和1045中碳鋼。12NiCr6鋼的化學(xué)成分(質(zhì)量分?jǐn)?shù)/%)為0.12C，1.6Ni，0.85Cr，0.76Al，0.6Mn，0.32Si，熱處理方式分別為880 ℃×1 h正火處理和880 ℃×1 h水淬+500 ℃回火處理；將這2種熱處理態(tài)的12NiCr6鋼分別記作NF鋼和TR500鋼。1080高碳鋼的化學(xué)成分(質(zhì)量分?jǐn)?shù)/%)為0.814C，0.12Si，0.598Mn，0.122Cr，0.23Cu，0.014S，熱處理方式為815 ℃×1 h油淬+480 ℃回火。1045中碳鋼的化學(xué)成分(質(zhì)量分?jǐn)?shù)/%)為0.47C，0.252Si，0.717Mn，0.012P，0.005Mo，0.003S，熱處理態(tài)為熱軋態(tài)。由拉伸試驗(yàn)測得試驗(yàn)鋼的力學(xué)性能參數(shù)如表1所示。

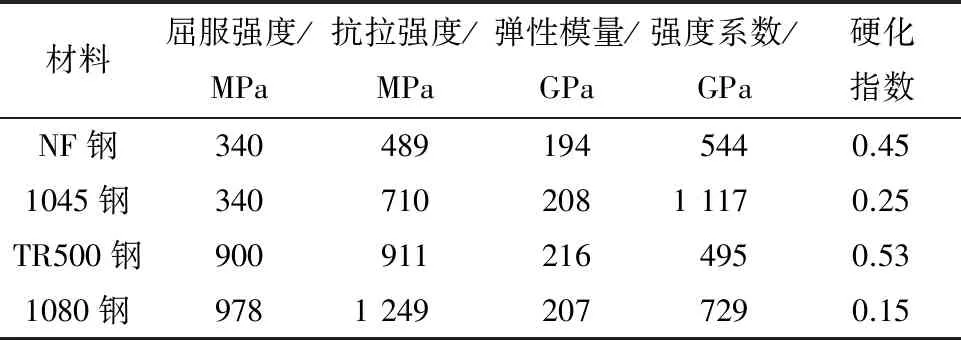
表1 不同試驗(yàn)鋼的力學(xué)性能參數(shù)Table 1 Mechanical property parameters of different test steels

根據(jù)ASTM E647，在試驗(yàn)鋼上截取CT試樣，試樣的厚度B為15 mm，寬度W為80 mm，初始裂紋長度a0為15 mm，CT試樣的尺寸以及DCPD測定方法如圖2所示。試驗(yàn)中將銷釘插入CT試樣的圓孔中，向兩端沿箭頭所示方向施加載荷P，在導(dǎo)線中通入穩(wěn)定的直流電，測定裂紋兩端電勢差V。通過DCPD軟件實(shí)時(shí)獲取并儲(chǔ)存循環(huán)次數(shù)及其對(duì)應(yīng)的應(yīng)力強(qiáng)度因子、電勢差等。由于DCPD試驗(yàn)過程中輸入的電流不變，所以電勢差信號(hào)與裂紋長度存在一定的函數(shù)關(guān)系，對(duì)于裂紋高度可忽略不計(jì)的CT試樣，通常采用Johnson公式[16]計(jì)算裂紋長度，該公式為

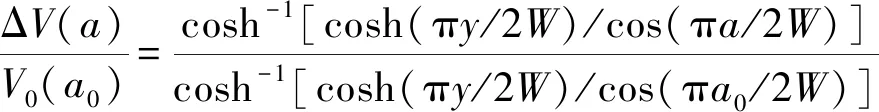
(8)

式中：a為裂紋長度；y為2個(gè)探頭間距離的一半；ΔV/V0為標(biāo)準(zhǔn)化電壓降；ΔV為實(shí)時(shí)電壓；V0為初始電壓。

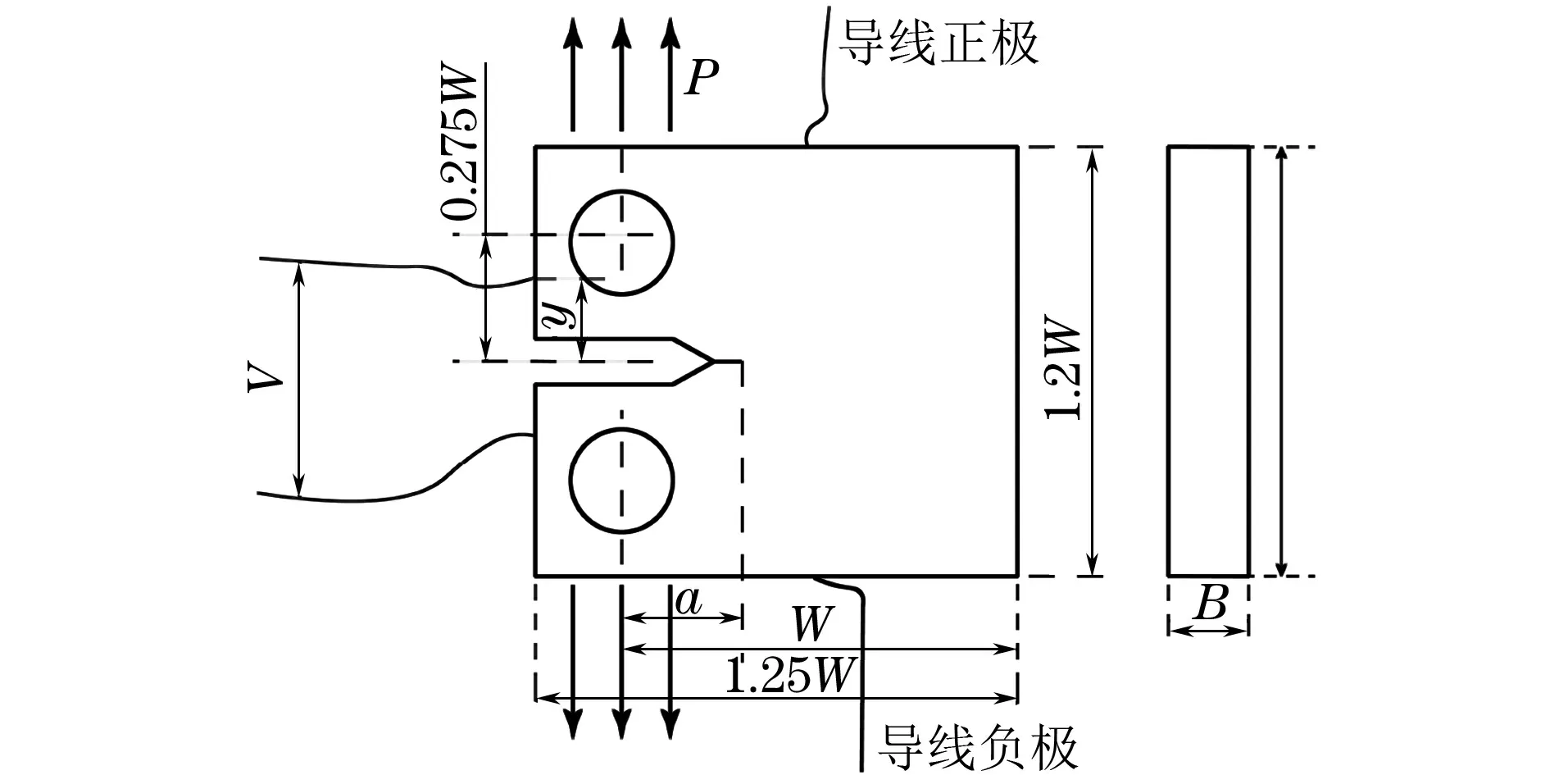
圖2 CT試樣的尺寸及DCPD方法示意Fig.2 Dimension of CT specimen and schematic of DCPD method

利用Johnson公式計(jì)算裂紋長度一般會(huì)產(chǎn)生一定的誤差，因此需要采用有限元方法在試驗(yàn)前對(duì)探頭兩端測得電勢差與裂紋長度進(jìn)行標(biāo)定。選用COMSOL軟件進(jìn)行有限元模擬，建立DCPD試驗(yàn)?zāi)Ｐ停脜?shù)掃描功能模型裂紋從初始長度a0擴(kuò)展10 mm的過程，記錄電勢數(shù)據(jù)。模擬得到裂紋擴(kuò)展1 mm(即裂紋長度為16 mm)時(shí)的電勢分布，結(jié)果如圖3所示。

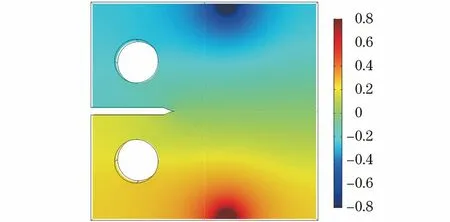
圖3 模擬得到裂紋擴(kuò)展1 mm時(shí)試樣的電勢分布Fig.3 Potential distribution of specimen with crack growth of 1 mm by simulation

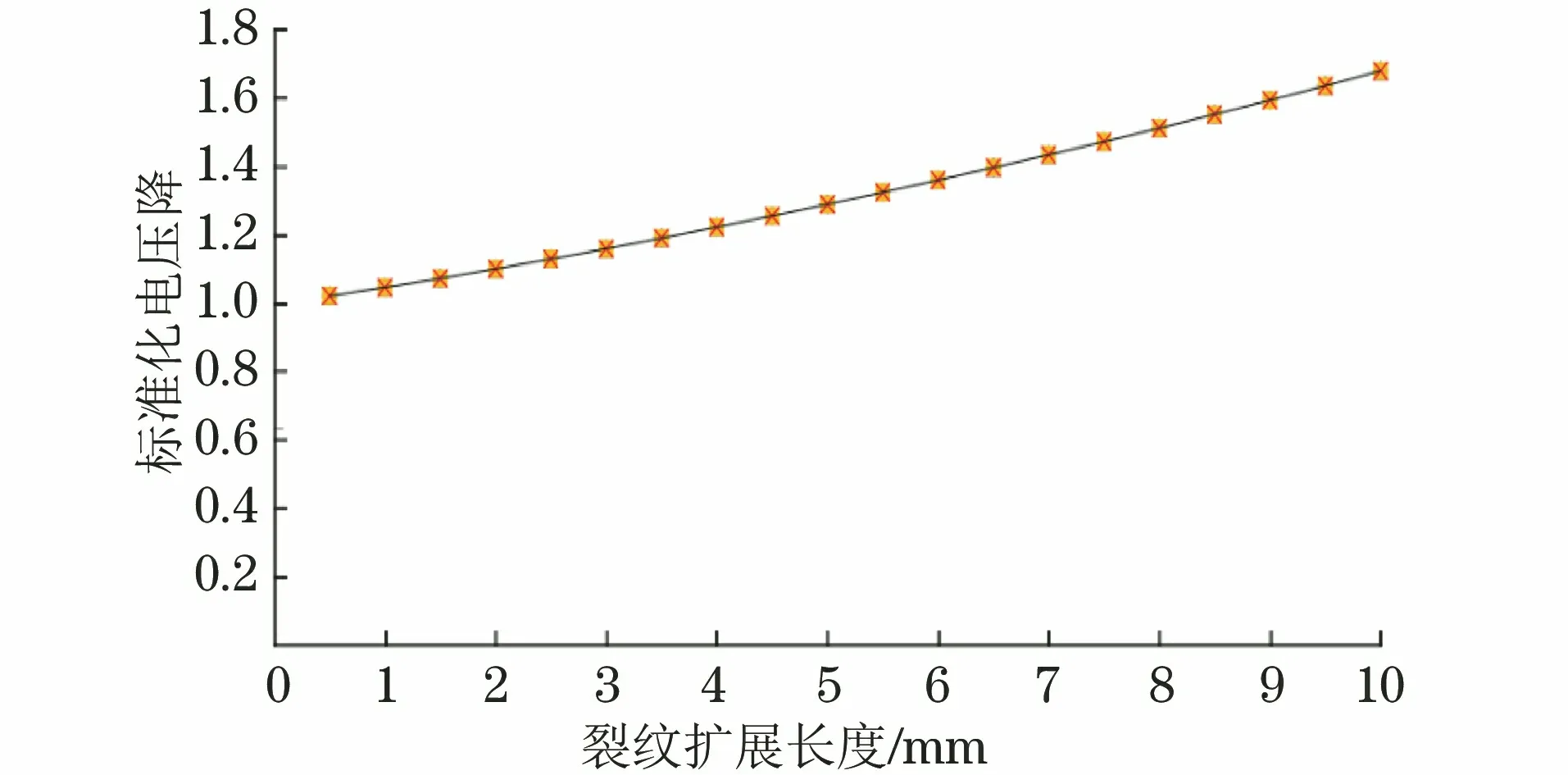
圖4 由標(biāo)定得到的標(biāo)準(zhǔn)化電壓降-裂紋擴(kuò)展長度曲線Fig.4 Curve of standardized potential drop-crack growth length by calibration

采用有限元仿真得到的不同裂紋長度及其對(duì)應(yīng)的兩探頭間的電勢差，擬合得到裂紋擴(kuò)展長度與標(biāo)準(zhǔn)化電壓降的關(guān)系曲線，結(jié)果如圖4所示。根據(jù)標(biāo)定得到的標(biāo)準(zhǔn)化電壓降-裂紋擴(kuò)展長度曲線，即可由DCPD方法測定的電勢差得到實(shí)時(shí)的裂紋長度，從而計(jì)算出實(shí)時(shí)裂紋擴(kuò)展速率。

為盡量減少測試誤差，在銷釘和探針外露部分均用絕緣膠帶包裹。為了使試樣在加載頻率為15 Hz時(shí)具有相同的標(biāo)準(zhǔn)塑性區(qū)尺寸，均采用應(yīng)力比R為0.1的ΔK進(jìn)行疲勞試驗(yàn)。在每次測試過程中均對(duì)試樣施加一個(gè)頻率為0.1 Hz的單峰過載，具體如圖5所示，圖中Kpic為過載時(shí)的最大應(yīng)力強(qiáng)度因子，Kmax為循環(huán)加載時(shí)的最大應(yīng)力強(qiáng)度因子。表2列出了不同試驗(yàn)鋼的試驗(yàn)參數(shù)，表中Rpic為過載率。采用降應(yīng)力強(qiáng)度因子法預(yù)制疲勞裂紋，即在裂紋萌生階段將ΔKmax從1.4ΔK降到ΔK。試樣的初始裂紋長度a0為15 mm，當(dāng)裂紋長度到達(dá)18 mm時(shí)結(jié)束預(yù)制，然后保持ΔK不變將裂紋擴(kuò)展至長度為20 mm，隨即施加單峰過載，再繼續(xù)使用ΔK進(jìn)行加載；當(dāng)DCPD軟件顯示的實(shí)時(shí)裂紋擴(kuò)展速率為正常速率并保持10 000周次循環(huán)穩(wěn)定后停止試驗(yàn)。

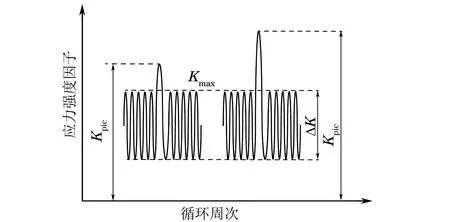
圖5 疲勞試驗(yàn)過程中施加的載荷示意Fig.5 Schematic of applied loads during fatigue test

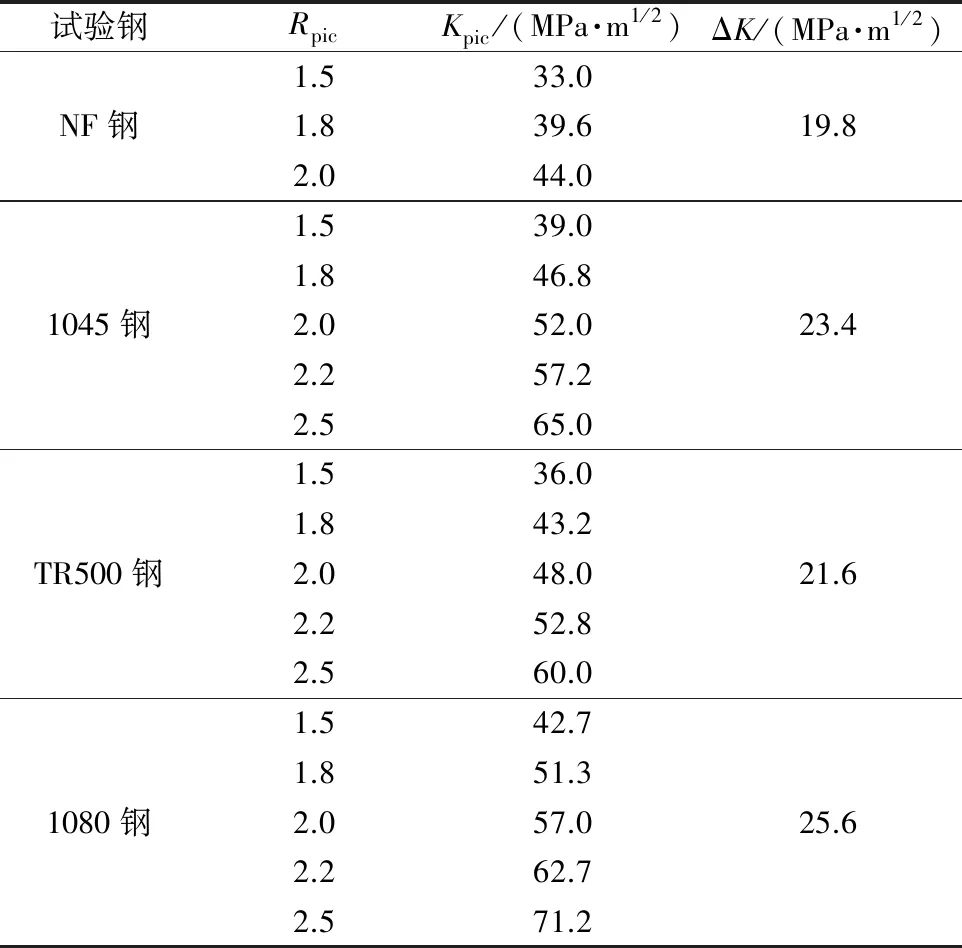
表2 不同試驗(yàn)鋼的疲勞試驗(yàn)參數(shù)Table 2 Fatigue test parameters for different test steels

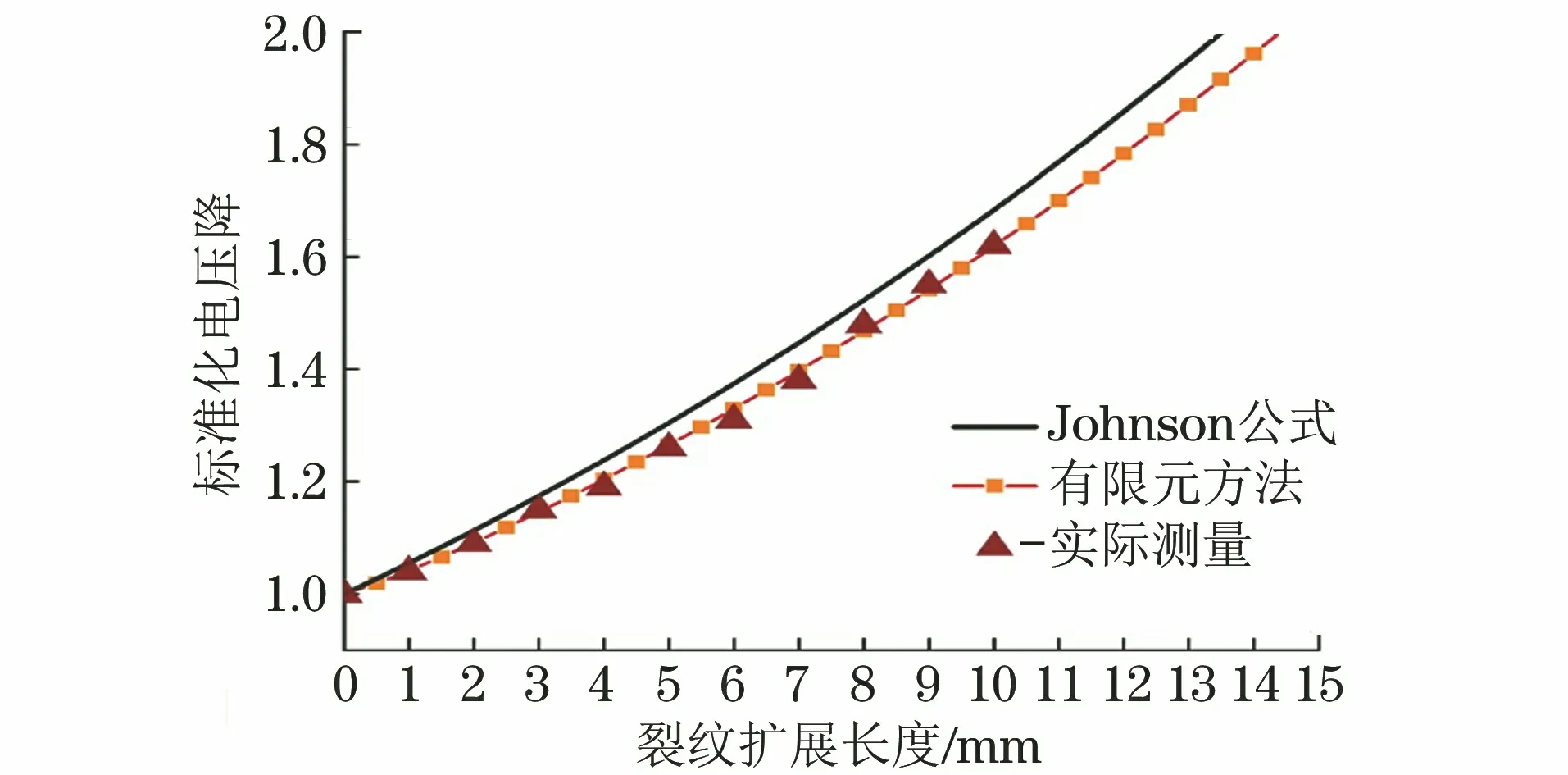
圖6 采用Johnson公式、有限元方法得到的標(biāo)準(zhǔn)化電壓降-裂紋擴(kuò)展長度關(guān)系與實(shí)測值的對(duì)比Fig.6 Comparison of relation between standardized potential drop and crack propagation length obtained by Johnson formula,finite element method and mearsured values

3 結(jié)果與討論

由圖6可以看出：由Johnson公式計(jì)算得到的標(biāo)準(zhǔn)化電壓降-裂紋擴(kuò)展長度關(guān)系與試驗(yàn)結(jié)果存在一定的誤差，而使用有限元方法得到的裂紋擴(kuò)展長度與試驗(yàn)結(jié)果間的誤差較小，相對(duì)誤差小于3.75%。由此可知，使用DCPD方法結(jié)合有限元標(biāo)定確定裂紋擴(kuò)展長度的準(zhǔn)確性與精度較高。

由圖7可以看出，單峰過載后，4種試驗(yàn)鋼的裂紋擴(kuò)展速率先下降到最低點(diǎn)后逐漸恢復(fù)到正常值，該現(xiàn)象即為過載延遲效應(yīng)。通過對(duì)比試驗(yàn)結(jié)果與模型預(yù)測結(jié)果可以看出，裂紋擴(kuò)展速率試驗(yàn)值與預(yù)測值的變化趨勢吻合度較高。其中，1080鋼的裂紋擴(kuò)展速率預(yù)測值與試驗(yàn)值的偏差較大，出現(xiàn)該問題的原因可能在于：(1)材料參數(shù)C，m具有一定分散性，導(dǎo)致過載后的裂紋擴(kuò)展速率預(yù)測值與試驗(yàn)值存在較大的偏差；(2)圖(1)所示的計(jì)算疲勞載荷下裂尖塑性區(qū)的Rice塑性疊加方法過于簡化，無法真實(shí)描述塑性區(qū)邊緣形狀與塑性區(qū)內(nèi)應(yīng)力分布，而且1080鋼為高強(qiáng)度鋼，裂尖塑性區(qū)較小導(dǎo)致應(yīng)力梯度過大，造成Rice方法計(jì)算的σres(x/W)與實(shí)際結(jié)果存在偏差。采用DCPD方法得到的試驗(yàn)數(shù)據(jù)非常穩(wěn)定，沒有產(chǎn)生噪點(diǎn)，說明該方法在測量裂紋疲勞擴(kuò)展速率中有非常好的穩(wěn)定性，且具有較高的準(zhǔn)確性。

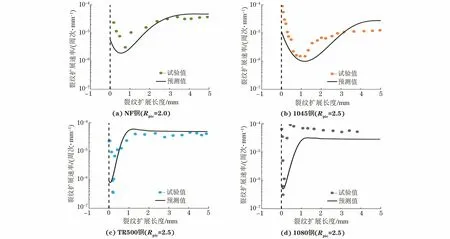
圖7 采用DCPD方法結(jié)合有限元標(biāo)定測得過載后不同試驗(yàn)鋼的裂紋擴(kuò)展速率試驗(yàn)值與驅(qū)動(dòng)力模型預(yù)測值的對(duì)比Fig.7 Comparison between experimental crack growth rate after overloading of different test steels obtained by DCPD method combined with finite element calibration and driving force model predicted values

由圖8可知：疲勞裂紋擴(kuò)展速率的延遲效應(yīng)主要由過載比決定，隨著過載比的增大，試驗(yàn)鋼在過載后的延遲效應(yīng)增大，過載延遲長度也增大，且屈服強(qiáng)度較低試驗(yàn)鋼的延遲效應(yīng)影響長度遠(yuǎn)大于屈服強(qiáng)度較高試驗(yàn)鋼的。

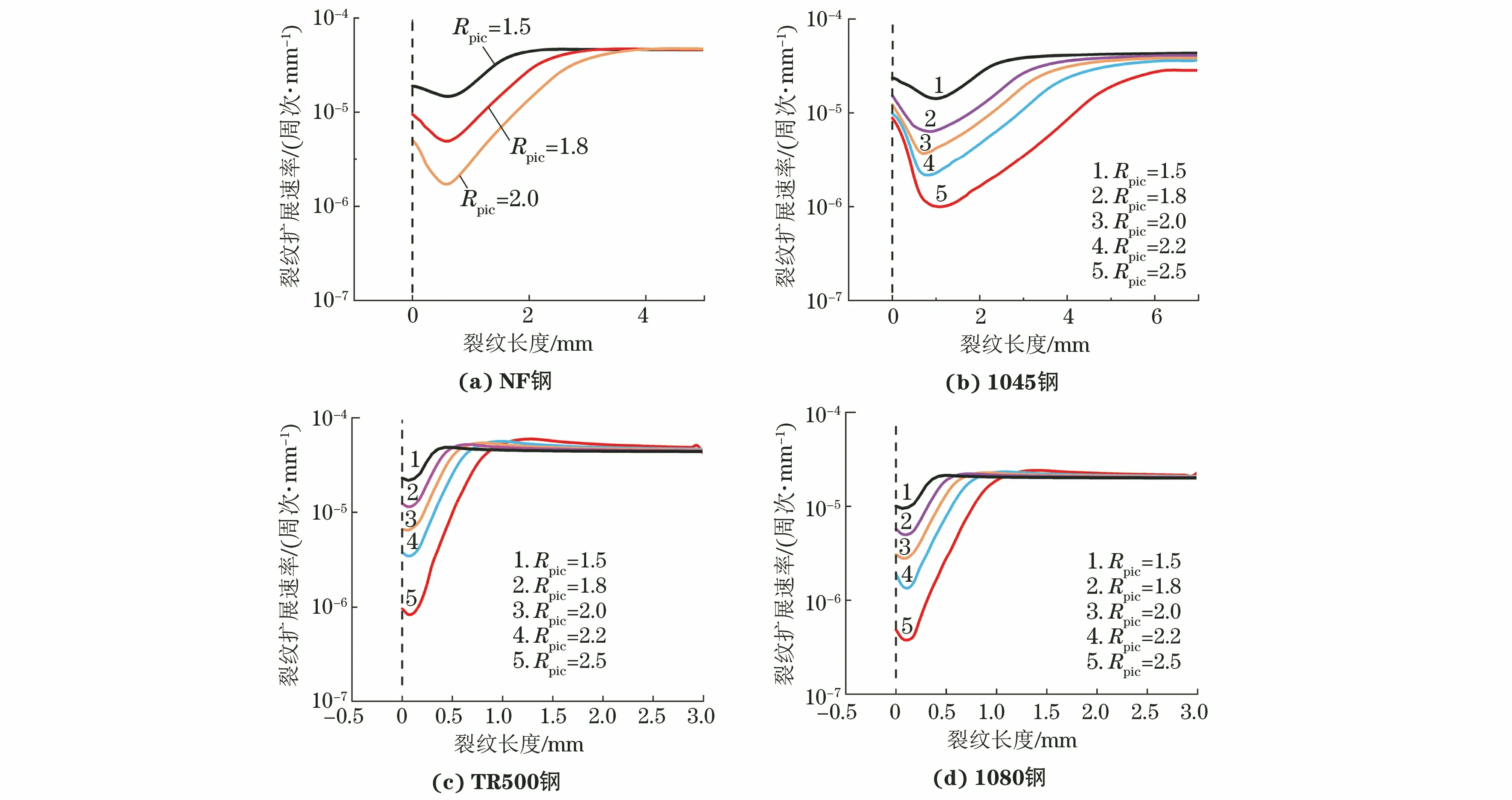
圖8 采用DCPD方法結(jié)合有限元標(biāo)定得到不同過載比下過載后不同試驗(yàn)鋼裂紋擴(kuò)展速率的擬合曲線Fig.8 Fitting curves of crack growth rate after overloading of different test steels under different overload ratios obtained by DCPD method combined with finite element calibration

由圖9可以看出：除1080鋼外的其他3種試驗(yàn)鋼的預(yù)測壽命都位于1.5倍誤差帶內(nèi)，預(yù)測效果較好；1080鋼的部分預(yù)測壽命的誤差偏大，但仍位于2倍誤差帶內(nèi)，這是因?yàn)椴牧蠀?shù)與裂尖塑性區(qū)內(nèi)應(yīng)力分布公式計(jì)算結(jié)果的偏差導(dǎo)致裂紋擴(kuò)展速率預(yù)測結(jié)果的偏差，進(jìn)而造成預(yù)測壽命的偏差。綜上可知，新型驅(qū)動(dòng)力模型的預(yù)測精度較高，適用性較廣，同時(shí)驗(yàn)證了DCPD方法在過載延遲效應(yīng)研究中的有效性。

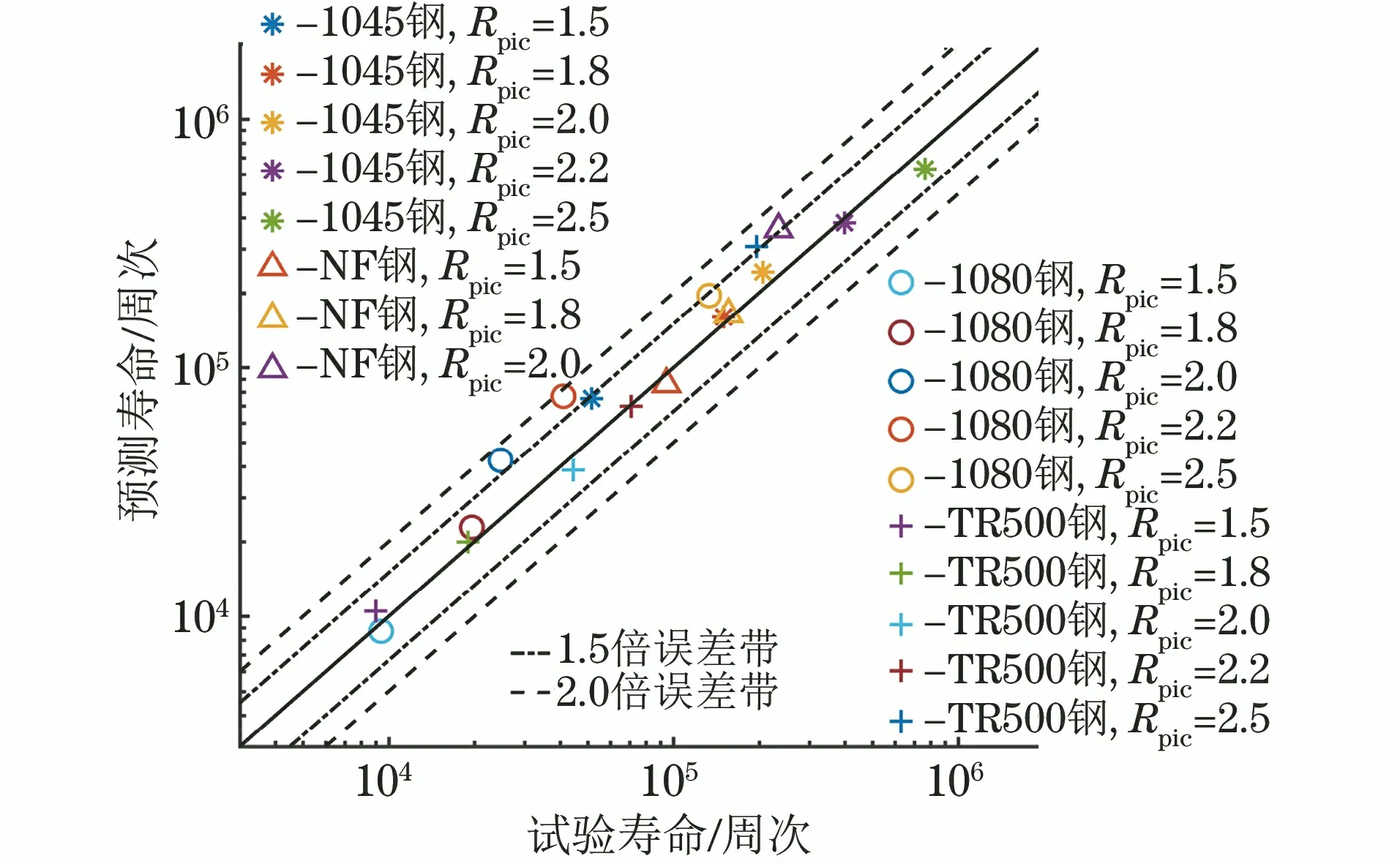
圖9 不同試驗(yàn)鋼在不同過載比下疲勞壽命預(yù)測結(jié)果與試驗(yàn)結(jié)果對(duì)比Fig.9 Comparison between predicted fatigue life and test results of different test steels under different overload ratios

4 結(jié) 論

(1) 單峰過載后，4種試驗(yàn)鋼的裂紋擴(kuò)展速率先下降到最低點(diǎn)后逐漸恢復(fù)到正常值,試驗(yàn)鋼出現(xiàn)過載延遲效應(yīng)；過載比越大，試驗(yàn)鋼過載后的最小裂紋擴(kuò)展速率越小，且屈服強(qiáng)度較低試驗(yàn)鋼的延遲效果較大。由DCPD方法結(jié)合有限元標(biāo)定得到的裂紋擴(kuò)展長度與實(shí)測值間的相對(duì)誤差小于3.75%，說明該方法具有較高的準(zhǔn)確性，且在測量裂紋疲勞擴(kuò)展速率中有非常好的穩(wěn)定性。

(2) 采用新型驅(qū)動(dòng)力模型預(yù)測得到裂紋擴(kuò)展速率的變化趨勢與由DCPD方法結(jié)合有限元標(biāo)定得到的試驗(yàn)值相吻合，4種試驗(yàn)鋼的預(yù)測延遲疲勞壽命均位于2倍誤差帶內(nèi)，新型驅(qū)動(dòng)力模型的預(yù)測精度較高，適用性較廣。