改進A＊算法與動態窗口法的機器人動態路徑規劃

槐創鋒，郭 龍，賈雪艷，張子昊

華東交通大學 機電與車輛工程學院，南昌330013

在移動機器人諸多技術的研究中，路徑規劃是技術研究中的重要部分之一，是機器人研究領域的熱點，目的是在有障礙物的環境中按照某一種評價指標尋找一條從起始點位置到目標點位置的最優無碰撞路徑[1-2]。

柵格法環境建模的經典方法，通過利用柵格對環境信息進行表示，柵格的大小決定了環境信息儲存量的大小以機器人進行路徑規劃的時間長短[3-4]。A*算法[5]是路徑規劃算法中經典的啟發式搜索算法。A*算法由Hart等[6]提出，結合Dijkstra算法和最佳優先搜索算法的優點。文獻[7]改進A*算法，在啟發函數中加入余弦相似性和方向信息，做歸一化處理。文獻[8]提出改進A*算法的擴展搜索鄰域的思路，利用最小二叉堆優化A*算法OPEN列表存儲結構提高搜索效率，但無法完成動態避障。文獻[9]成功地擴大搜索鄰域，通過重新定義中心節點的位置，在每個節點的周圍擴大無限可搜索鄰域，較為快速實現無碰撞路徑規劃。文獻[10]基于A*算法，設計了優化的啟發搜索函數，選取策略是使用關鍵點，剔除多余路徑點以及非必要的轉折點。文獻[11]通過引入二次A*算法，減少路徑軌跡冗余點，縮短路徑長度并且采用自適應圓弧優化算法與加權障礙物步長調節了算法，采用預瞄偏差角追蹤法捕捉移動目標點，有效提升路徑規劃效率。文獻[12]以時間耗費作為評價指標，假設AGV 通過每個弧或節點的時間成本是固定的，改進A*算法通過搜尋最小時間耗費來選擇最優路徑。文獻[13]A*算法的改進，創新了高層建筑逃生路徑規劃算法，對節點擴展優化、權值優化方面進行改進。文獻[14]修改A*算法的地圖信息，擴展了一層障礙物，改進了代價函數F作二次擴展，并且考慮機器人半徑。

針對傳統路徑規劃算法無法高效地、安全地完成動態環境下的路徑規劃，將傳統A*算法擴展搜索鄰域，去除了擴展鄰域同方向的子節點，改進成了7×7 的A*算法。然后基于改進7×7的A*算法和動態窗口法的移動機器人在柵格法環境模型中實時仿真動態路徑規劃。

1 改進的A＊算法

1.1 傳統A＊算法

A*算法是啟發式的搜索算法，可以實現全局路徑規劃。根據定義的估價函數在靜態環境模型中搜索理論上的最優路徑，則代價函數表示為：

式中，n代表當前節點；f(n)是當前節點n的代價函數；g(n)為移動機器人起始節點到達當前節點n的實際代價值；h(n)是從當前節點n到達目標點的代價估計值，是代價函數中最重要的部分，正確地選擇h(n)能夠提升A*算法的成功率和準確性。選取歐氏距離作為h(n)的代價函數，函數表示為：

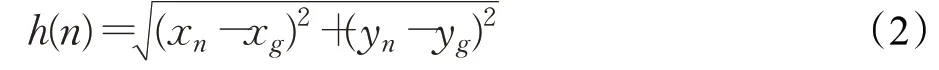
式中，(xn,yn)代表當前路徑節點所在柵格中心的坐標，(xg,yg)代表目標點節點所在柵格中心坐標。傳統的A*算法搜索從起始點到達目標點的最優路徑過程中，規劃的全局路徑存在多余節點，運動軌跡折線較多，在路徑節點處存在轉折角度過大以致于不符合移動機器人運動學原理等缺陷，為此提出一種改進的A*算法。

1.2 改進7×7的A＊算法

傳統A*算法搜索擴展節點采用3×3 鄰域算法，如圖1 所示。任意搜索方向之間夾角均為0.25π，節點轉折角均為0.25π 的倍數，因此傳統A*算法的規劃路徑不是理論最短，而且規劃路徑上因為轉折點較多、轉折角過大不夠平滑。

圖1 傳統3×3的A*算法鄰域搜索圖

針對傳統A*算法3×3 的鄰域搜索缺陷，提出擴展A*算法搜索鄰域。以圖1中7×7正方柵格圖為例，當前節點n位于中心節點，其周圍第一層（3×3 的鄰域）中8個節點是傳統A*算法待擴展的節點。改進算法除了采用3×3鄰域搜索算法外，還采用當前節點n周圍第二層即5×5 的搜索鄰域，共計16 個節點納入算法待擴展節點，算法待搜索鄰域節點數即為24個，節點移動方向是16個方向，改進之處在于去除同方向的多余子節點，則改進5×5的A*算法待搜索節點個數減少為16個。這樣既擴大了搜索鄰域，優化了搜索角度，又提高了算法效率，如圖2 所示。當A*算法的擴展搜索鄰域到達第三層，如圖3所示為7×7的搜索鄰域，去除同方向的多余子節點后，待搜索鄰域個數為32，可移動方向為32，則將傳統A*算法成功改進為7×7的A*算法。

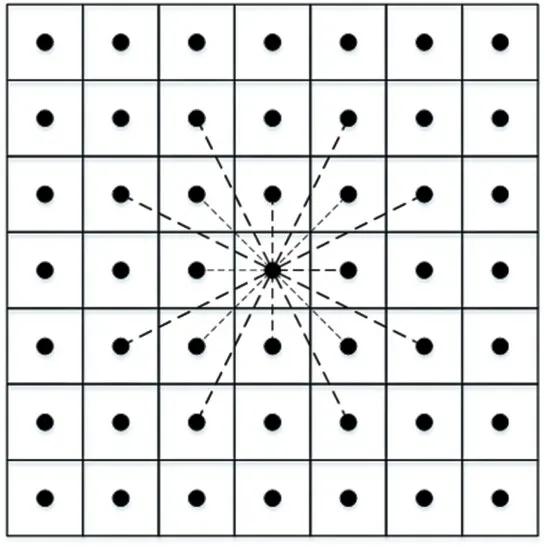
圖2 改進5×5的A*算法鄰域搜索示意圖

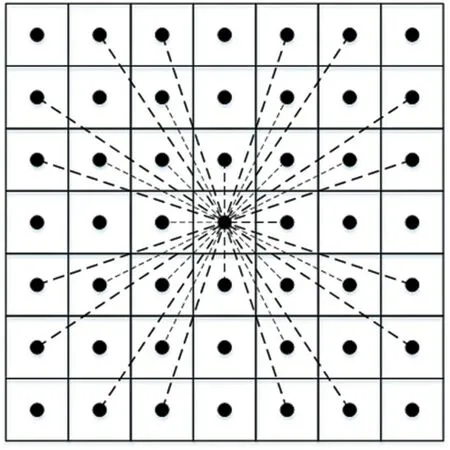
圖3 改進7×7的A*算法鄰域搜索示意圖

2 動態窗口算法

傳統DWA 算法進行規劃時，缺少全局規劃路徑的指引，只有目的地位置方向的指引，而中間具體路徑是對環境中的障礙物及時避障實時規劃的路徑[15]。然而，在障礙物較多情況下，移動過程容易陷入局部最優，導致全局路徑距離變大。將改進的7×7的A*算法與動態窗口算法進行融合，在局部路徑規劃時，機器人對臨時設置的未知動態障礙物成功規避，安全高效地到達目標點位置，完成了全局路徑規劃。

動態窗口法，是基于機器人運動學和動力學的一種局部路徑規劃算法，將路徑規劃問題轉化成為速度矢量空間上的約束優化問題。動態窗口法的目的是：在速度二維空間中采樣多組速度（線速度、角速度），在一定時間間隔內，同時模擬移動機器人在這些速度下的軌跡。獲取多組可行軌跡后，根據設計的評價函數，選取最優軌跡所對應的速度（線速度、角速度），驅動機器人完成局部路徑規劃。

2.1 機器人運動學模型

動態窗口算法針對窗口區域內移動機器人的速度進行空間采樣，并且模擬出移動機器人的運動軌跡。機器人的運動狀態由機器人的線速度和角速度來反饋，(vt,wt)表示軌跡，通過評價函數在所有可行軌跡里選取最佳軌跡，在時間間隔Δt內，假設機器人作勻速直線運動，運動學模型為：

2.2 機器人速度采樣

在速度空間中存在無窮多組(v,ω)，要依據機器人的實際情況對采樣速度的范圍進行約束。

（1）機器人的速度約束為：

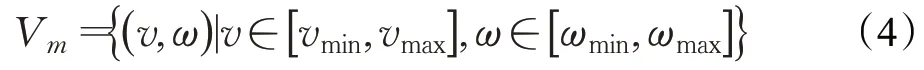
（2）機器人電機加減速約束。動態窗口移動時間間隔內，機器人加速度所帶來的最大、最小速度為：

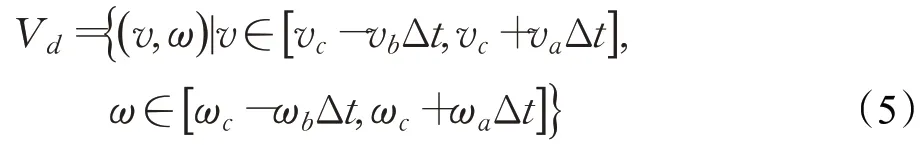
式中，vc、wc代表當前速度；va、wa代表機器人最大加速度；vb、wb代表機器人最大減速度。

機器人制動距離約束。在局部路徑規劃時為了確保機器人安全，在最大減速度條件要求下，機器人在撞擊障礙物之前速度減為0，則：

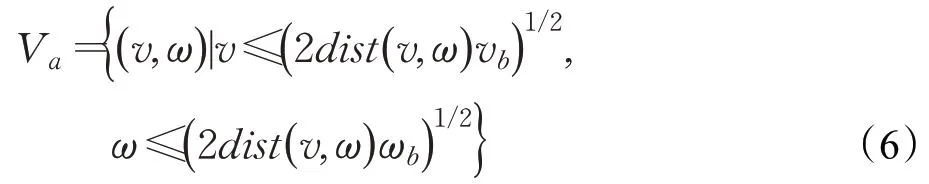
式中，dist(v,w)是(v,w)對應軌跡距離障礙物的最近距離。

2.3 機器人評價函數

速度空間存在若干組的采樣速度是可行的，于是設計評價函數以便選取機器人最優軌跡。評價函數設計準則為局部路徑規劃，機器人應盡量避開障礙物，用最短時間到達目標點位置。設計的評價函數為：

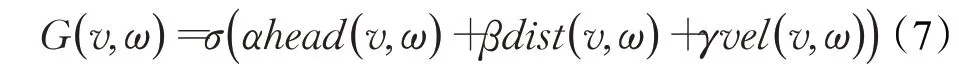
式中，方位角評價函數head(v,w)，代表了當前速度下模擬軌跡終點位置方向與目標位置之間的方位角偏差；軌跡與靜態障礙物的最近距離為dist(v,w),vel(v,w)為當前模擬速度大小的評價函數；σ為平滑系數；α、β、γ為3項的加權系數。

3 融合算法

傳統DWA 算法進行規劃時，缺少全局規劃路徑的指引，只有目的地位置方向的指引，故采用改進7×7 A*算法進行全局路徑規劃，融合動態窗口法進行動態避障，提升動態規劃路徑的全局最優性。

為了提升實時避障在路徑轉彎處的能力，提高路徑平滑性，在避障過程中，需要實時預估路徑的彎曲程度，遇到急彎時提前減速。為每個子目標點Gi添加一個參數Δθ表示全局路徑在該子目標點的彎曲程度，Δθ是Gi分別與前后兩個相鄰子目標點的夾角。當Δθ接近π時，相鄰兩個子目標點連線的方向近乎平行，機器人以較高的速度運行，當Δθ接近直角時，路徑的彎曲程度較大，機器人應降低速度規劃平滑路徑準備轉彎。當運動軌跡近乎直線時，機器人線速度較大，當路徑需要避障轉彎時，線速度降低，增加路徑平滑度。

為避免動態窗口算法陷入局部最優，設計了一種全局最優路徑的動態窗口評價函數：

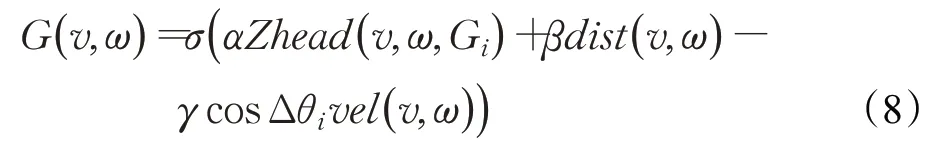
式中，Zhead(v,w,Gi)為模擬軌跡終點方向與子目標點之間的方位角偏差。Δθi是Gi分別與前后兩個相鄰子目標點的夾角，子目標點Gi是機器人靜態規劃下的前進方向上距離當前點最近的靜態環境下的全局最優路徑點。此評價函數使得局部路徑規劃遵循全局路徑規劃路徑序列點，從而保證全局路徑最佳。

3.1 完成全局規劃和臨時動態避障

為驗證所提融合算法在復雜環境中進行動態路徑規劃的有效性，在所建的柵格圖環境模型中，首先標定目標點的位置和機器人起始點的位置，應用算法進行仿真驗證，圖4柵格地圖環境中可以看出機器人避開所有靜態障礙物到達目標點位置，完成了靜態環境下路徑規劃。

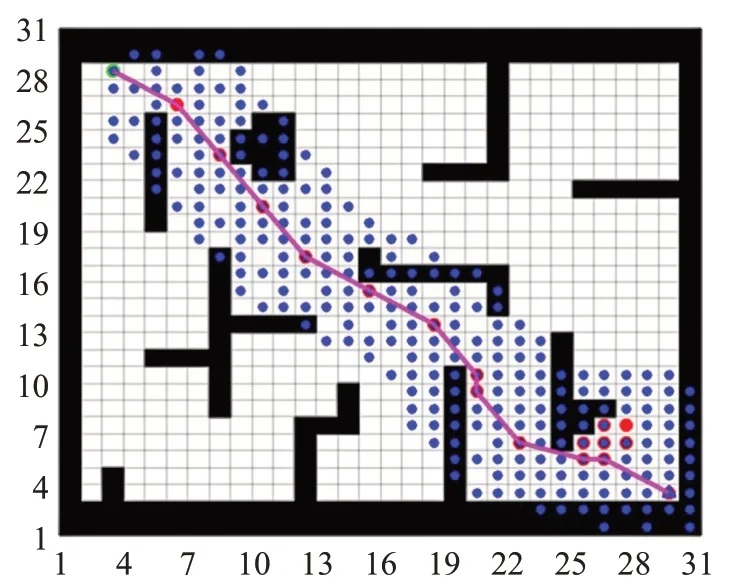
圖4 融合算法靜態環境路徑規劃

為了驗證動態環境下的路徑規劃，在機器人規劃好的路徑上臨時設置動態障礙，紅色的方塊即為設置的動態障礙物。圖5中的運動軌跡是機器人規劃好的路徑，在路徑上放置障礙物，綠色的箭頭為機器人的運動方向。圖6 為移動機器人初始到結束動態路徑規劃的過程圖，顯示了移動機器人成功地避開動態障礙物到達目標點位置。從圖5、6 可以看出，改進的融合算法，可以實現局部路徑規劃，躲避動態障礙物，還能得到平滑而且安全的規劃路徑。

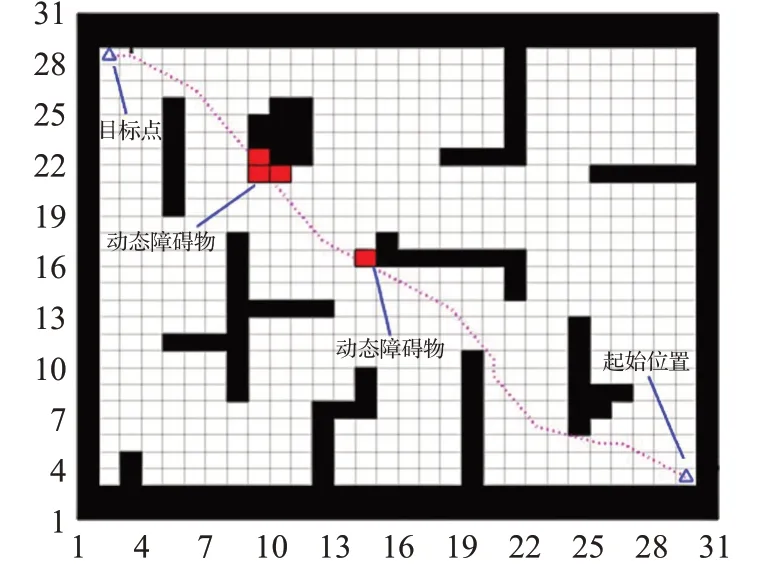
圖5 臨時設置動態障礙物

3.2 輸出運動參數

所改進的融合算法可實時輸出機器人的控制參數，有利于機器人的自動反饋控制，機器人線速度的變化、機器人姿態（弧度）的變化、機器人角速度的變化結果如圖7 所示。圖7 反映了機器人動態路徑規劃時，控制參數的變化，當機器人局部路徑躲避障礙物時，線速度減小，弧度也減小。

3.3 驗證算法高效性和適用性，對比其他算法

圖6 動態避障路徑規劃圖

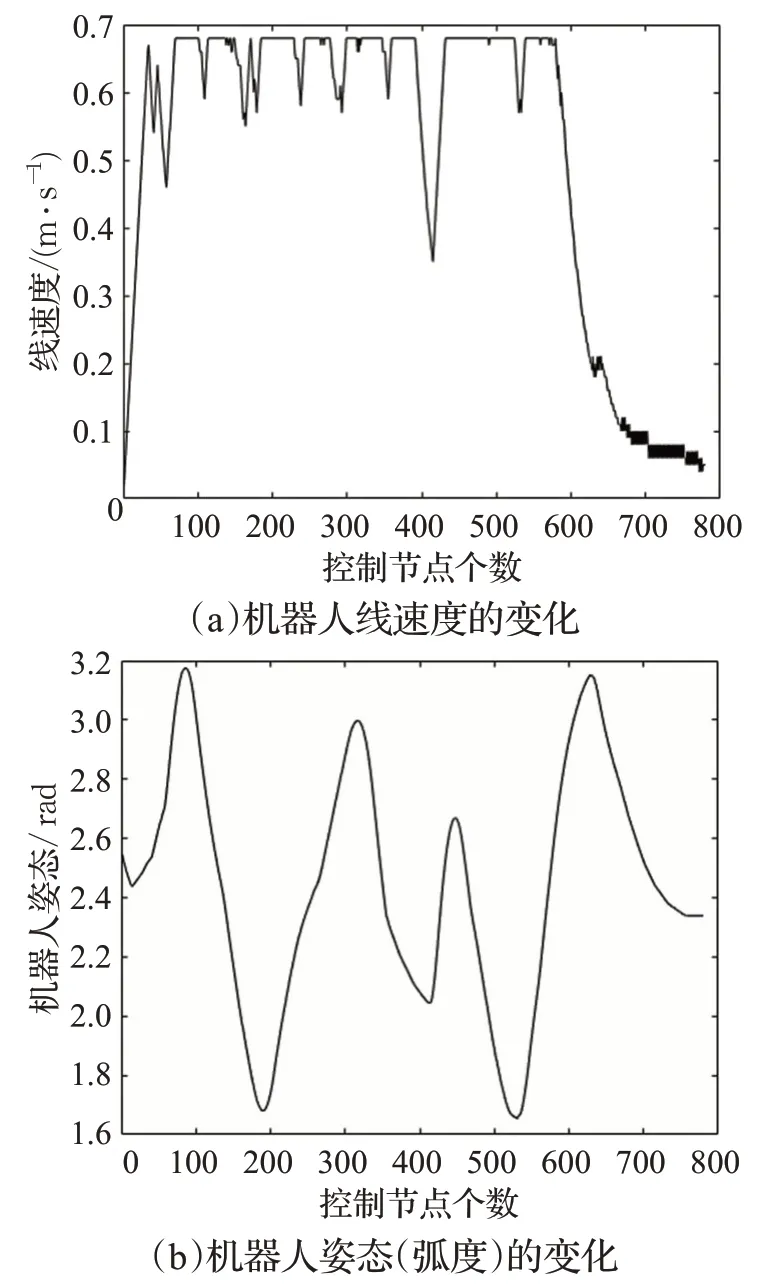
圖7 機器人的控制參數變化圖

為了驗證基于改進7×7的A*算法與動態窗口法的融合算法的高效性，與標準A*算法、改進7×7的A*算法在相同的仿真環境中作出對比，仿真實驗結果如圖8所示。每組重復仿真10 次，取平均值記錄路徑規劃的時間和路徑長度，各種算法的性能指標如表1所示。

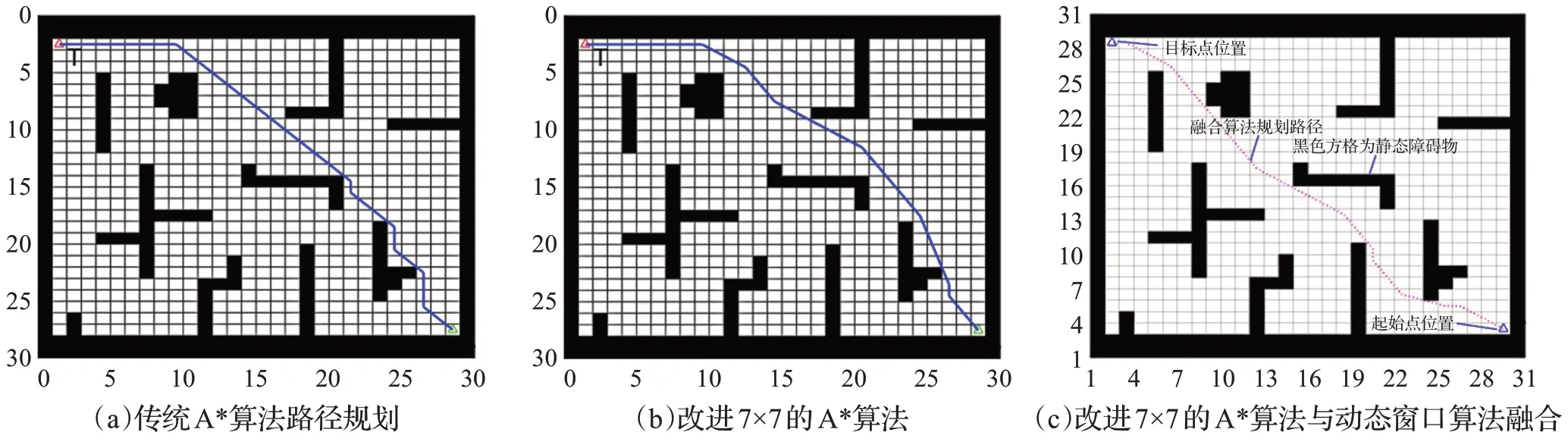
圖8 三種算法全局路徑規劃仿真圖

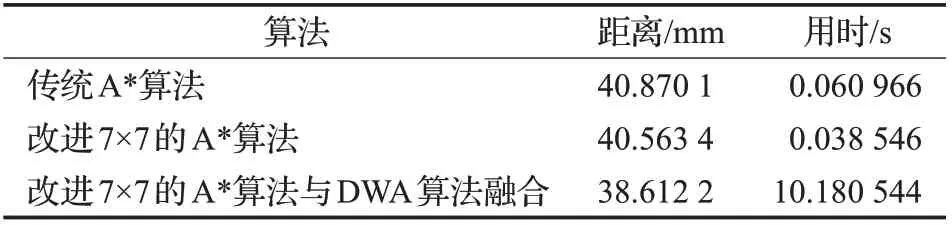
表1 三種算法性能指標的對比

由圖8、表1可知，三種算法都能夠在靜態環境下規劃出從起始點到目標點的路徑。傳統A*算法路徑轉折角多，轉折角度大，改進的7×7的A*算法平滑性最好，路徑最短，用時最少。

將3×3的搜索鄰域擴展為7×7后，同時去除擴展鄰域同方向的多余子節點，實質上搜索方向由8個增加到32個，優化了搜索角度；從表中可以看出改進7×7的A*算法距離為40.563 4 mm，時間為0.038 546 s。傳統A*算法路徑距離為40.870 1 mm，時間為0.060 966 s。改進7×7的A*算法增加了搜索方向，并沒有因為增加算法計算量而延長路徑規劃時間，相反因為優化了搜索角度，取消了節點移動方向僅為0.25π的整數倍的限制，提高了搜索效率，因此減少了路徑規劃時間；并且改進7×7的A*算法優化了全局路徑，減少了路徑長度，增加了路徑平滑性，可以表明改進7×7 的A*算法比傳統A*算法更具有適用性。

相比傳統A*算法和改進7×7 的A*算法，基于改進7×7的A*算法與動態窗口算法的融合算法，規劃路徑更短為38.612 2 mm，平滑性更好，路徑規劃更好。

4 結論

將傳統A*算法，擴展其搜索鄰域同時去除了同方向的多余子節點，改進為一種7×7的A*算法，有效地消除了傳統路徑轉折角多、轉折角度大的缺陷。為提升在動態復雜環境下移動機器人路徑規劃效率，提出一種基于改進7×7的A*算法與動態窗口法的融合算法，設計了一種全局最優路徑的動態窗口評價函數，采用動態窗口算法實現路徑的局部規劃，成功規避了擋住已規劃好路徑上的動態障礙物，機器人規劃出了從起始點到目標點的最優路徑。通過與多種算法仿真分析比較，結果表明了提出的融合算法具有可行性和高效性。