基于高斯變異與Levy飛行策略的混合粒子群優化算法*

謝金宵,高岳林，*，于宏利

(1.北方民族大學 數學與信息科學學院,寧夏 銀川 750021；2.北方民族大學 寧夏智能信息與大數據處理重點實驗室,寧夏 銀川 750021)

1995年，JAMES KENNEDY博士和RUSSELL EHERHART博士共同提出了粒子群算法(PSO)[1]，該算法受鳥群在遷徙或覓食過程中的運動規律所啟發，將食物或棲息地看成所求問題的解，將鳥群飛行的空間比作問題的求解空間，鳥群中的每一只鳥被視為沒有質量和體積的微粒，作為問題的待選解[2]，問題的求解過程被比作鳥群在尋找食物或棲息地的過程。由于粒子群算法具有簡單、易實現、魯棒性強等好的性質，在函數優化，調度問題及工業、交通等實際問題中有著廣泛的應用。但與其他智能算法類似，PSO同樣存在著許多不足之處。例如，所得到的解精度低，容易出現早熟收斂[3]等問題。一直以來，國內外許多學者為解決上述不足，做了許多方面的努力，使PSO在性能上有了很大的進步。然而大多數改進機制主要關注于對粒子群算法中的參數進行優化，而忽略了使算法陷入局部最優解和收斂速度慢等問題的底層機理，所以很難使算法從根本上解決上述不足。文獻[4]將遺傳算法中的選擇算子融合到粒子群算法中，從而改善了算法的收斂性。文獻[5]將差分進化算法與粒子群算法融合,提高了算法全局尋優能力。文獻[6]利用粒子群算法優化核極限學習機的核參數,有效提高了單核極限學習機分類器的性能。文獻[7]改進了多目標粒子群算法(MOPSO)，實現了交流濾波器多目標優化設計。文獻[8]加入了混合蛙跳算法的分組思想，提出了一種蛙跳簡化粒子群算法,改進的算法能夠有效地避免早熟收斂問題,并能較大幅度地提高收斂速度和收斂精度。本文針對PSO求解精度低、全局搜索能力不足的缺點，提出了一種GLPSO算法，將高斯變異與Levy飛行策略引入到算法中，使算法更好地保持種群多樣性，降低過早陷入局部最優解的可能，提高了算法的全局搜索能力和求解精度。

1 基本粒子群算法

在PSO中，首先隨機初始化一批粒子作為問題的初始解[9]，同時初始化每個粒子的位置和速度。在每一次迭代中，每個粒子憑借所有粒子在搜索的歷史上最優的記錄，既全局最優值坐標gbest和粒子在飛行過程中自身歷史上最優的記錄(個體最優值坐標)，其迭代公式如下：

vt+1=ωvt+c1r1(pbestt-xt)+

c2r2(gbestt-xt)，

(1)

xt+1=xt+vt+1，

(2)

其中，ω是慣性系數，它是影響算法搜索性能的重要參數，其取值的大小表示粒子對當前個體速度的繼承量；c1和c2均稱為加速因子，其中c1稱為認知系數，表示粒子的自我認知經驗，c2稱為社會系數，表示粒子從當前全局最優解中學習的能力；r1和r2是介于[0,1]之間相互獨立的隨機數；pbest是粒子i極值點的坐標，gbest是全體粒子全局極值點的位置[10]。

PSO算法的具體步驟如下：

步驟1初始化種群，給定種群數量、初始位置及速度；

步驟2計算種群中所有個體的適應能力；

步驟3根據步驟2中每個個體和適應能力更新全局最優值和個體最優值，更新公式如下:

(3)

(4)

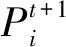
步驟4根據式(1)與(2)更新每個個體的位置與速度;

步驟5若達到終止條件，算法結束。否則，返回執行步驟2。

2 基于高斯變異與Levy飛行策略的混合粒子群優化算法

2.1 Levy飛行

Levy飛行是由法國數學家Levy提出的一種符合Levy分布的隨機游走模型[11]，從其過程來看具有馬爾可夫性質，自然界中很多鳥類及昆蟲的飛行軌跡符合Levy分布[12]。Levy飛行過程模擬的步幅多數情況下較小，偶爾也會出現較大步幅，其公式[13]如下：

(5)

其中，Levy(β)是服從參數為β的Levy分布，0<β<2，μ服從N(0,σ2)分布，ν服從N(0,1)分布，σ可由式(6)計算得到：

(6)

其中，Γ表示Gamma分布函數，β=1.5，Levy飛行隨機游走模擬圖像如圖1所示，其中橫坐標與縱坐標給出了粒子搜索空間范圍。為更一般表示Levy飛行的性質，圖1中所涉及的步長為無量綱的單位步長。

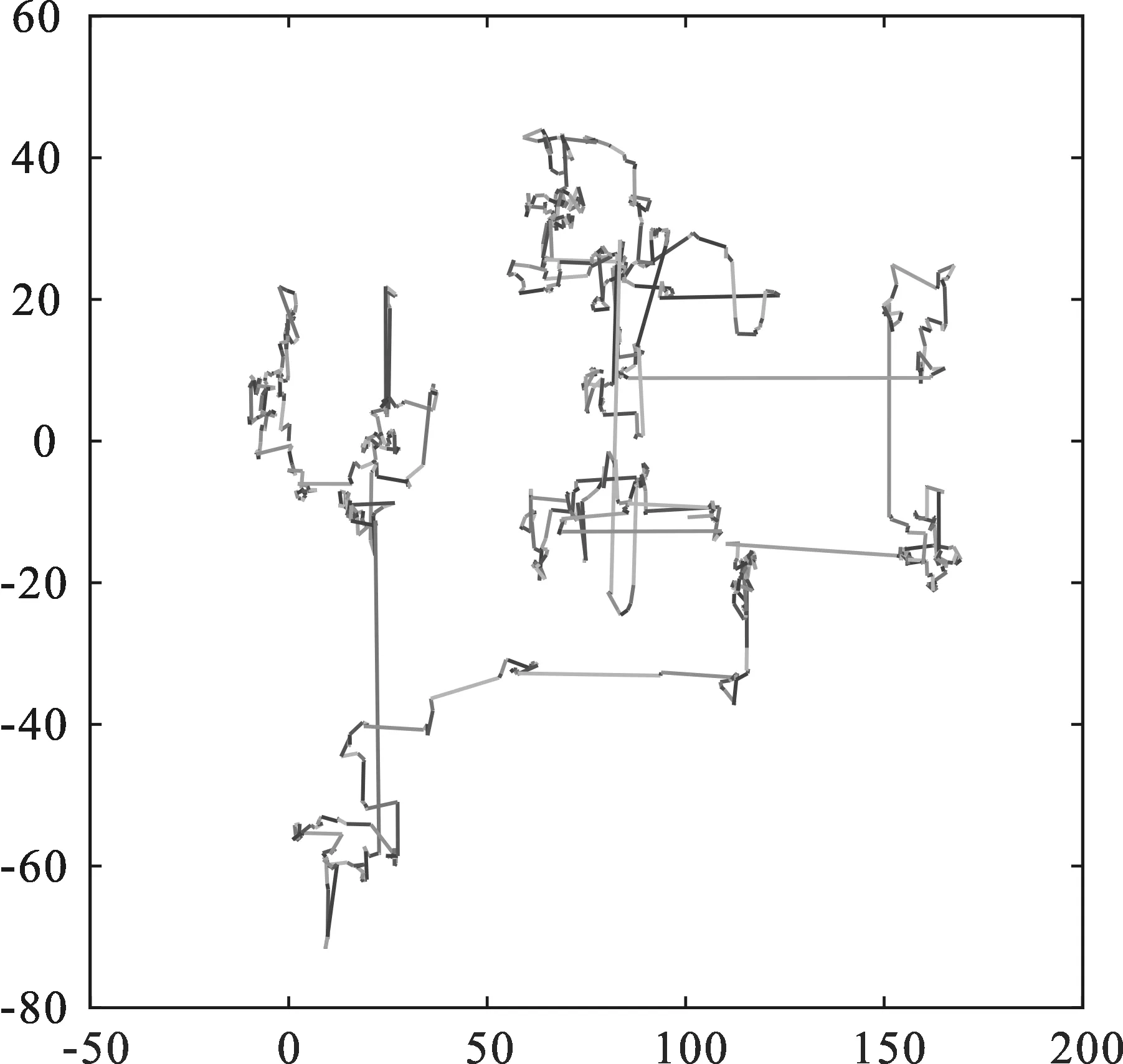
圖1 Levy飛行模擬圖像Fig. 1 Levy flight simulation image

2.2 高斯變異

多數群智能算法中，其位置更新主要依靠個體間的信息相互交流，算法本身不具備變異能力從而使算法容易陷入局部最優解。高斯變異[14]是在原有種群狀態上加入服從高斯分布的狀態函數，公式如下：

xk=xk×[0.5+τ×N(0,1)]，

(7)

其中，xk是種群中粒子迭代k次之后的狀態，τ是[0,1]之間的一個隨機變量，N(0,1)是均值為0，方差為1的正態分布。在原有粒子種群運動的基礎上，加入隨機的正態分布擾動項，從而有利于算法減少陷入局部最優解的可能，增強全局尋優能力。

2.3 GLPSO算法流程

GLPSO是在PSO基礎上通過引入Levy飛行策略和高斯變異算子，使算法具有更高的全局尋優能力和更加優良的種群多樣性，其算法流程如下：

步驟1初始化種群；

步驟2計算種群中每個粒子的適應度；

步驟3根據每個個體和適應度更新全局最優值和個體最優；

步驟4根據Levy飛行，更新每個粒子的飛行方式，公式如下:

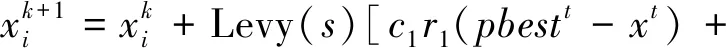
(8)

步驟5記錄每次迭代后的最優值，在全局最優值迭代10次不發生改變后，認為算法陷入局部最優解，則執行步驟6，否則執行步驟7；

步驟6對種群中的個體進行高斯變異操作；

步驟7算法達到終止條件，則執行步驟8，否則執行步驟2;

步驟8輸出算法全局最優解。

3 GLPSO算法收斂性分析

3.1 群智能隨機算法收斂的充分條件

SOLIS et al[15]已證明群智能隨機算法依概率1收斂于全局最優解的充分條件為以下2點：

條件1：如果F(f(z,τ))≤F(z)，并且若τ∈S，則F(f(z,τ))≤F(z)，其中F為待求解函數，f為生成解函數，z為S中的一個點，其能保證F有一個下確界，τ是一個隨機生成向量[16]。

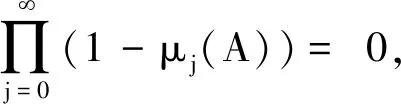
3.2 GLPSO算法收斂性證明

引理1GLPSO算法滿足條件1。

證明在GLPSO算法中，函數f可定義為：

f(pbk+1,gbk+1)=

(9)

由于GLPSO算法總是保留問題更優的解，即采用精英保留策略，所以算法滿足條件1。

引理2GLPSO算法滿足條件2。

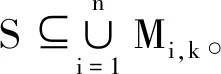
Mi,k=x(t)+ω(x(t-1))-

x(t-2)+φ1(pi-x(t-1))+
φ2(pg-x(t-2)),

(10)

其中0≤φ≤c1，0≤φ2≤c2。可知，Mi,k為一個超矩形，其中一個頂點為(φ1,φ2)=(0,0)，另外一個頂點為(φ1,φ2)=(c1,c2)。

當

max{c1|pi-x(t-1)|,

c2|pg-x(t-1)|}≤0.5diamj(S)

成立時，v(Mi,k∩S)≤v(S)。diamj(S)表示解空間S第j維分量的長度。由于xi收斂于(φ1pi+φ2pg)/(φ1+φ2)，故Mi,j→0。隨著迭代次數k的增加,v(Mi,k∩S)逐漸減小，從而存在一個正整數K,當k>K時，有A?S，因為有支撐集Mi,k=S,同時令S的Borel支撐子集為A=Mi,k[17],則

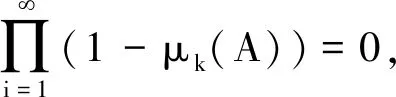
定理1GLPSO算法搜索序列依概率1收斂于全局最優解。

證明因為GLPSO算法滿足條件1與條件2，因此GLPSO算法搜索序列依概率1收斂于全局最優解。

4 數值實驗與結果分析

4.1 測試函數與參數設置

為驗證GLPSO算法的有效性，本文將GLPSO算法與基本PSO算法及帶有慣性因子的WPSO算法進行了比較，選用的測試函數見表1，其中列出了所用測試函數的搜索范圍、理論最優值和維數。參數設置如下：c1=2，c2=2，ω=0.75，N=100，GLPSO算法中β=1.5。其余參數均相同。

表1 測試函數Tab. 1 Test functions

4.2 實驗結果分析

通過上述給定的5個經典測試函數對GLPSO算法的尋優能力進行分析，并與PSO算法和WPSO算法進行對比。為保證實驗的有效性，所有算法的最大迭代次數均設為200次。各算法對每個測試函數獨立運行40次，并求40次計算結果的最優值、最差值、平均值與方差。表2-表6給出了各算法之間的實驗數據對比結果。

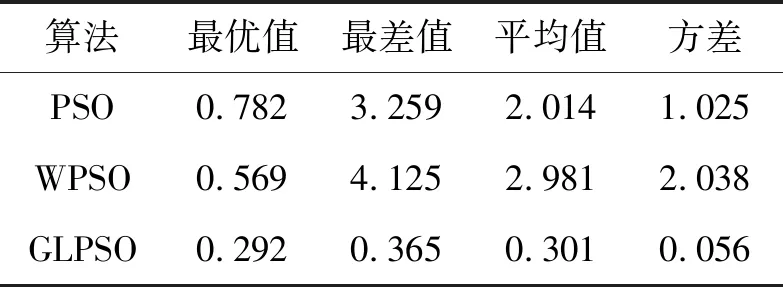
表2 函數F1實驗結果比較Tab. 2 Experimental results of function F1

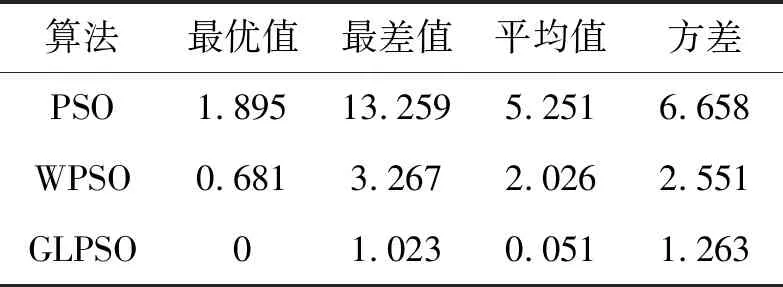
表3 函數F2實驗結果比較Tab. 3 Experimental results of function F2

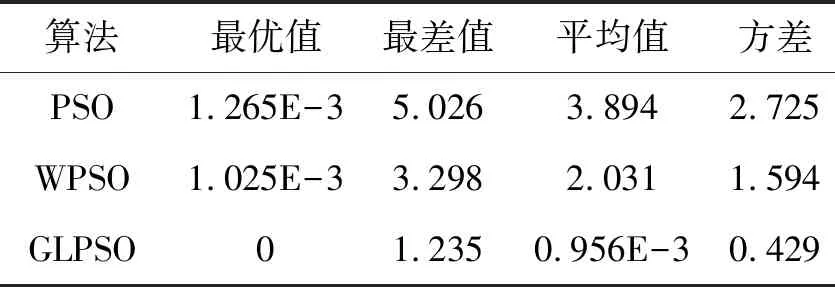
表4 函數F3實驗結果比較Tab. 4 Experimental results of function F3

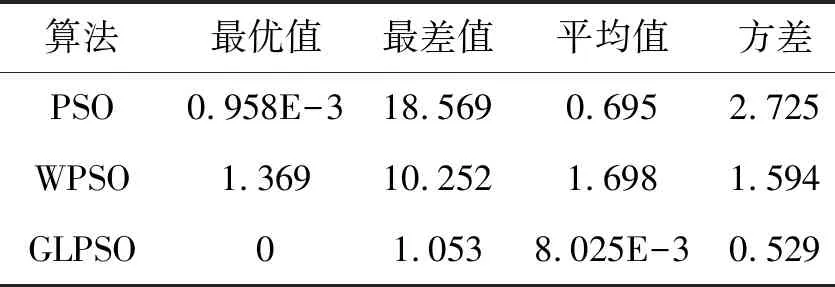
表5 函數F4實驗結果比較Tab. 5 Experimental results of function F4

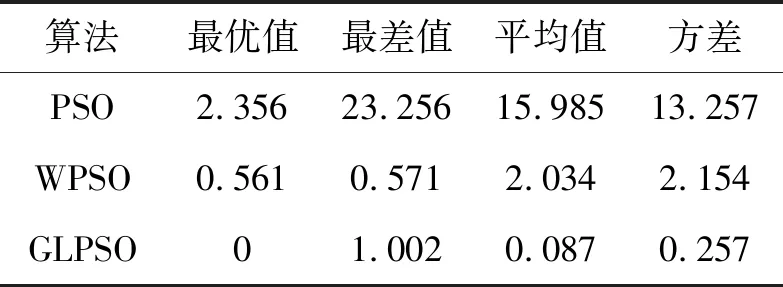
表6 函數F5實驗結果比較Tab. 6 Experimental results of function F5

由表2-表6可知，PSO算法在尋優過程中有很大的概率陷入局部最優值，在3個算法的比較中效果最差。WPSO算法在引入慣性系數后改進了算法的尋優能力，提高了算法的尋優精度和全局搜索能力，但WPSO算法的求解精度和搜索能力與GLPSO相比并不令人滿意，算法求解精度仍然偏低。本文所提出的GLPSO算法融合了高斯變異與Levy飛行方法，使算法中的種群具備了變異能力，提高了算法的全局尋優性能，使算法更容易跳出局部最優解。GLPSO算法在最優值、最差值、方差和平均值方面均優于PSO和WPSO算法，這表明GLPSO尋優精度高，擁有更好的優化能力，算法的穩定性更高。

為進一步分析算法的性能，圖2-圖6給出了算法在優化不同函數時的收斂圖像。

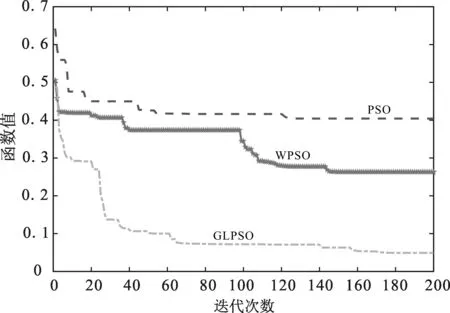
圖2 F1函數收斂曲線Fig. 2 Convergence curve of F1 function

由圖2，圖3，圖5可知，GLPSO與PSO和WPSO相比其求解精度更高，算法不容易陷入局部最優，有更強的全局尋優能力。由圖4可知，GLPSO優勢并不明顯，但從實驗數值上來看，依然優于對比算法。由圖6可知，GLPSO收斂速度更快，并由數值實驗結果分析，GLSPO有更高的求解精度。

圖3 F2函數收斂曲線Fig. 3 Convergence curve of F2 function

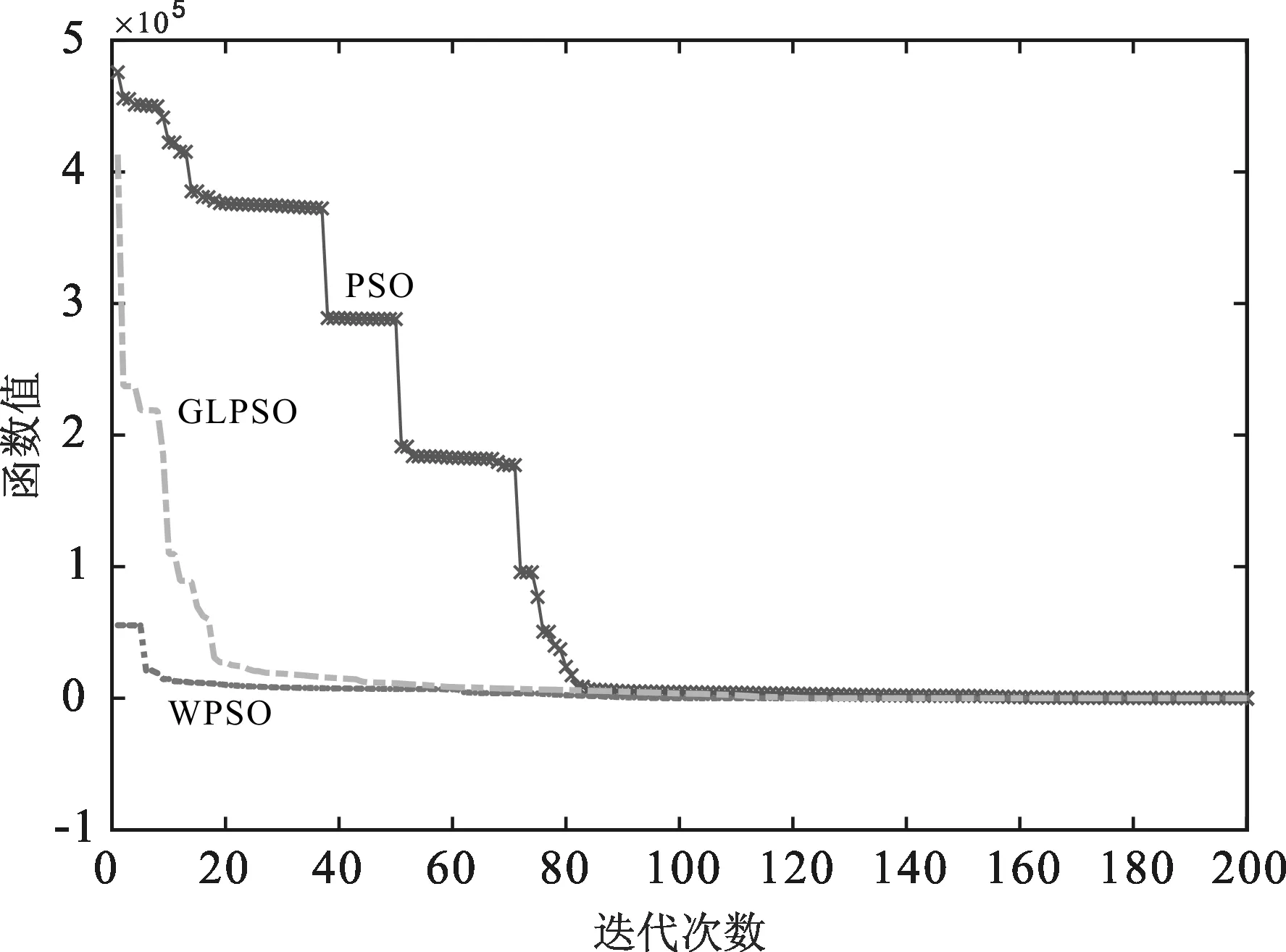
圖4 F3函數收斂曲線Fig. 4 Convergence curve of F3 function

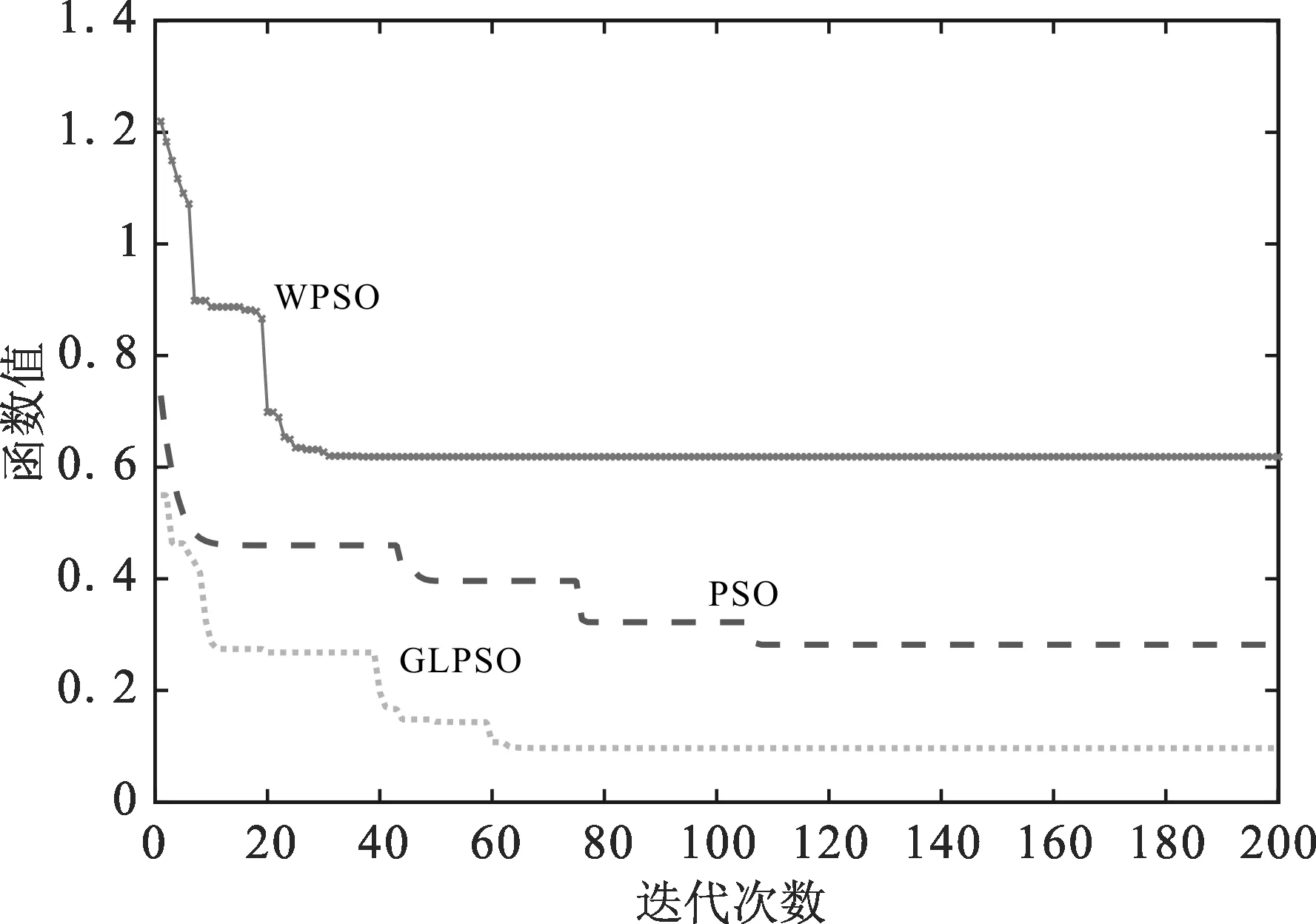
圖5 F4函數收斂曲線Fig. 5 Convergence curve of F4 function

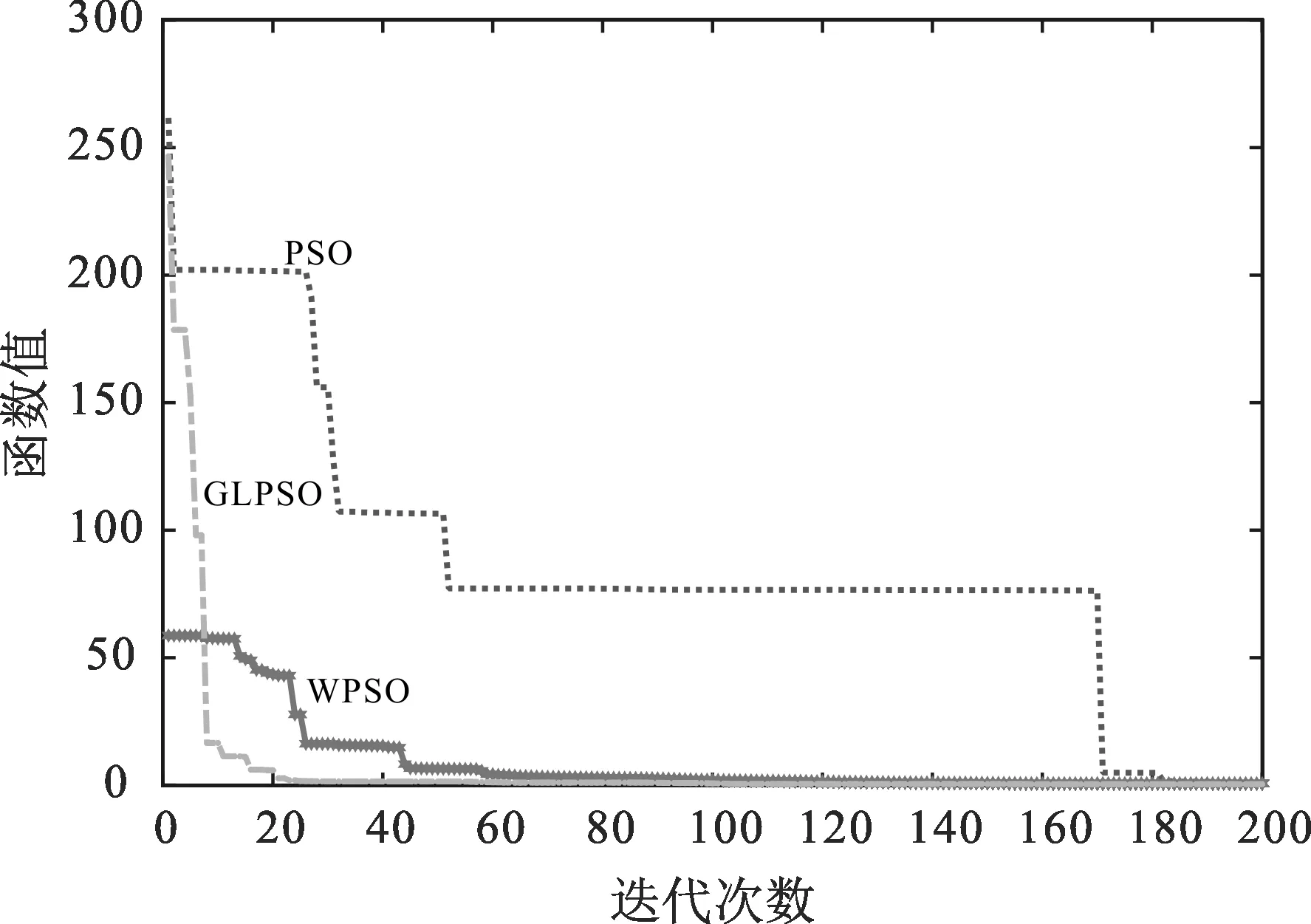
圖6 F5函數收斂曲線Fig. 6 Convergence curve of F5 function

5 結語

本文在 PSO 原理的基礎上引入具有跳躍性質的Levy飛行策略，并將高斯變異算子引入到算法中，使算法中的群體具有了變異能力，有效地保持了種群多樣性，減小了陷入局部最優的概率。通過5個經典函數對GLPSO算法的性能測試結果表明，GLPSO算法相對于基本PSO算法與帶有慣性系數的WPSO算法，具有更高的求解精度和更強的全局尋優能力。因此，該算法擁有更廣闊的應用前景。