“一帶一路”沿線主要國家股指市場風險傳染效應*

喬新堯,盧俊香,2*

(1.西安工程大學 理學院，陜西 西安 710048； 2.西安理工大學 經濟與管理學院，陜西 西安 710048)

2013年9月，習近平總書記在中亞和東南亞國家交流訪問期間，提出了“一帶一路”的倡議。隨著“一帶一路”的提出，中國與其他“一帶一路”沿線國家之間金融市場的聯系日益緊密。研究“一帶一路”對股票市場波動的影響，以及中國和沿線主要國家股票市場間的相關結構，有利于為中國進一步推進“一帶一路”建設、加強與沿線各國的貿易合作以及共同維護金融市場的穩定；可以為各個國家金融市場的監管部門提供一些參考，更利于給投資者進行投資組合時提出合理建議以減小投資風險。

金融時間序列大多呈現出尖峰厚尾、波動聚集性的特點。1959年，SKLAR首次提出了Copula函數的概念，將多維隨機變量的聯合分布函數與各邊際分布函數連接起來[1]，為學者們研究變量之間的相關關系提供了一個新的方法。EMBRECHTS et al首次將Copula函數應用到金融管理領域，提供了新的研究金融市場相關結構的方法[2]。MOKNI et al將GARCH模型和Copula函數結合起來共同研究股票市場的相關性[3-4]。國內，張堯庭首次詳細介紹了Copula函數的理論并將其運用于金融風險分析中[5]。劉紅玉運用Copula函數研究了上證綜指與深證成指的相關結構[6]。曹境鴿運用GARCH(1,1)-GED-Copula模型度量ETF基金投資組合的風險，發現相關性較強的投資組合的風險要高于相關系數小的組合風險[7]。

但是之前大多是借助單一的Copula函數研究兩兩資產間的相關結構，如果要研究2只以上股票之間的相關性及度量投資組合風險價值，單一的Copula函數明顯存在著局限性。HU最早提出了混合Copula函數模型(M-Copula) 來度量變量之間的相關關系[8]。ZILKO et al通過多元混合 Copula 函數對金融市場進行研究[9]。國內，陳秋林等建立M-Copula模型并計算VaR值[10-12]。徐麒等利用M-Copula函數研究消費者價格指數(CPI)和生產者價格指數(PPI)兩者間的相關性，結果表明CPI和PPI在經濟衰退時期的相關性更強[13]。劉祥東等運用M-Copula函數度量我國4個行業指數投資組合的風險價值，發現4個行業指數具有下尾相關性，更可能在同一時間發生下跌的情形[14-15]。在刻畫高維金融市場的相關結構時，選取M-Copula函數模型比單一的Copula函數更靈活，為研究多個變量之間的相關關系拓寬了思路。

同時，風險度量對投資者來說至關重要。最初，MARKOWITZ提出了均值方差模型來描述風險[16]，但是金融時間序列往往不服從正態分布，因此也有局限性。 隨后，摩根公司提出了VaR指標，成為銀行、證券公司等進行度量投資風險的重要工具。鄭文通最早將VaR方法引入中國，全面地介紹了VaR方法[17]。李麗梅等研究了由股票指數和股指期貨組合的VaR，發現SVt-EVT-Vine Copula 模型度量的投資組合風險更準確合理[18]。DU et al用Copula函數來分別研究匯率以及銀行的相關關系，并計算其風險價值[19-20]。在度量風險方面，VaR方法明顯比均值方差模型效果好。

在“一帶一路”背景下，對于沿線主要國家金融市場相關結構的研究日益被重視。王滿倉等根據協同理論分析了離岸金融與“一帶一路”之間的關系[21]；黃雯晶利用溢出指數模型研究中國與其他沿線國家股市間的波動溢出效應[22]。這些研究基本是從政治經濟學的角度來分析“一帶一路”背景下金融市場的相關結構，沒有運用簡單的數學模型以及大量數據實證。另外，國內外對于金融市場的相關結構的研究集中于金磚國家、發達國家，很少有涉及“一帶一路”沿線國家。因此，在已有的多維金融市場的相關性研究基礎上，本文以VaR作為風險度量指標，先使用GJR-GARCH(1,1)-t模型來刻畫各股指市場收益率的邊緣分布；再運用M-Copula函數來連接各邊緣分布刻畫股指市場間的相關結構；最后計算不同權重、不同置信水平下的資產組合的風險價值。

1 相關理論

1.1 邊緣分布

在構建多維金融市場的相關結構之前，需要先確定單變量的邊緣分布。研究表明，金融收益率序列往往呈現出“尖峰厚尾”“有偏”，并且還會出現波動聚集性的特征。 GLOSTEN et al提出了GJR-GARCH模型[23]，該模型能更準確地捕捉金融序列的波動聚集性和“杠桿效應”。考慮到收益率序列的厚尾性，本文擬用刻畫金融序列厚尾性的t分布結合GJR-GARCH模型擬合股指收益率殘差。GJR-GARCH(1,1)-t模型如下:

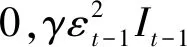
1.2 M-Copula函數模型

Copula函數的概念由1959年SKLAR回答多維聯合分布函數和邊緣分布之間的關系時提出，即聯合分布函數可以由Copula函數和邊緣分布函數共同表示，數學表達式如下：

F(x1,x2,…,xn)=

C(F1(x1),F2(x2),…,Fn(xn)),

(4)

其中，x1,x2,…,xn為n個隨機變量，F(x1,x2,…,xn)為變量x1,x2,…,xn的聯合分布函數，F1(x1),F2(x2),…,Fn(xn)分別為變量x1,x2,…,xn的邊緣分布函數，C(F1(x1),F2(x2),…,Fn(xn))為n元Copula函數，當F1(x1),F2(x2),…,Fn(xn)連續時，Copula函數唯一。

如果對(4)式求導，得到：

f(x1,x2,…,xn)=

(5)

其中，f(x1,x2,…,xn)表示變量x1,x2,…,xn的聯合密度函數，fi(xi)為變量xi(i=1,2,…,n)的密度函數，且

c(F1(x1),F2(x2),…,Fn(xn))=

令ui=Fi(xi),i=1,2,…,n，則

(5)式表明多元聯合密度函數f(x1,x2,…,xn)可由多元Copula函數c(F1(x1),F2(x2),…,Fn(xn))與各邊緣密度函數fi(xi)(i=1,2,…,n)乘積共同表示。

金融領域最常用的Copula函數多屬于橢圓類Copula函數族和阿基米德Copula函數族。不同類型的Copula函數對于變量之間的相關性的捕捉程度有所不同。其中，橢圓類Copula函數(正態-Copula和t-Copula函數)刻畫對稱的尾部相關結構；阿基米德族Copula函數(Gumbel-Copula, Clayton-Copula和Frank-Copula函數)分別描述非對稱的上尾相關結構、非對稱的下尾相關結構以及對稱的相關結構。由于不同的Copula函數刻畫不同的尾部相關結構，因此將幾種Copula函數組合起來，即混合Copula函數模型(M-Copula)共同研究相關結構，擬合的比只使用單一Copula函數的好。本文將Gumbel-Copula，Clayton-Copula和Frank-Copula函數線性組合起來共同研究5只股指間的相關結構。五元M-Copula函數的模型如下：

CM(u1,u2,u3,u4,u5)=ω1Cg(u1,u2,u3,u4,u5;θ1)+

ω2Cc(u1,u2,u3,u4,u5;θ2)+ω3Cf(u1,u2,u3,u4,u5;θ3)。

其中，CM(u1,u2,u3,u4,u5)為M-Copula函數，Cg(u1,u2,u3,u4,u5;θ1)表示Gumbel-Copula函數，Cc(u1,u2,u3,u4,u5;θ2)表示Clayton-Copula函數，Cf(u1,u2,u3,u4,u5;θ3)表示Frank-Copula函數；ω1,ω2和ω3(ω1,ω2,ω3≥0)為權重，且滿足ω1+ω2+ω3=1。

1.3 M-Copula模型的參數估計

一般采用極大似然估計法(Maximum Likelihood Estimate，MLE)來估計Copula函數的參數，但是M-Copula模型中不僅包含各Copula函數的參數，而且包括各權重參數。因此在估計該模型中的參數時，僅僅使用MLE方法是遠遠不夠的，需要在MLE方法的基礎上結合EM算法和BFGS算法。具體方法如下：

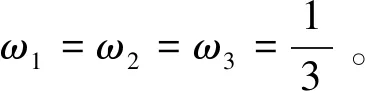
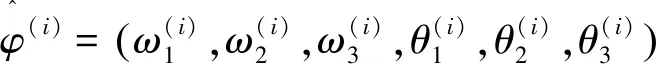
Step3: EM算法的E步，即求出增加了缺失數據后的完整數據Y后的對數似然函數關于缺失數據的條件期望：

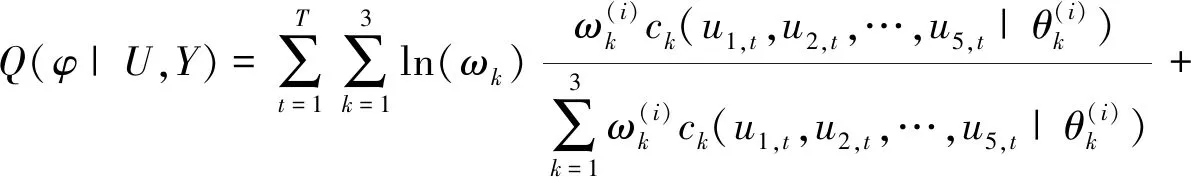
Step4: EM算法的M步，即對上式求最大值。在此步中，采用BFGS算法來進行。

1.4 M-Copula-GJR-GARCH(1,1)-t模型下的投資組合的風險價值

在險價值(Value at Risk, VaR)方法是度量金融市場投資組合的風險的主流方法。VaR指在給定置信水平的條件下，由于金融市場波動而導致的資產組合在未來一段時間內可能出現的最大價值損失，即P(Y≥VaR)=α，其中，Y表示金融資產(或組合)在未來某時間內所承受的損失值。Y=-R，R表示金融資產的收益，α為置信水平。

本文使用Monte Carlo模擬方法計算基于M-Copula模型的投資組合的VaR。模擬過程為:

(1) 根據已得到的M-Copula模型，模擬出N組服從均勻分布的Copula隨機向量(u1,t,u2,t,u3,t,u4,t,u5,t),t=1,2,…,T，T為Monte Carlo模擬的次數。

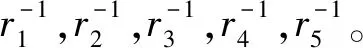
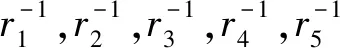
(4) 通過GJR-CARCH(1,1)模型的波動率方程，得出T+1天每只股票可能的日收益率Ri(i=1,2,…,5)。

(6) 根據P(Y≥VaR)=α計算資產組合的風險價值。

2 實證分析

本文在“一帶一路”背景下，選取2013年10月8日至2019年11月15日“一帶一路”沿線5個國家的股指數據的日收盤價，分別為滬深300指數、俄羅斯RTS指數、富時新加坡STI指數、孟買SENSEX30指數、日經225指數(數據來源為Wind數據庫)，得到實際有效數據共1 492組(刪除了股票收盤價缺失值，使得5只股指數據的收盤日期相同)。對日收盤價一階差分并擴大100倍：

rt=100×[ln(Pt)-ln(Pt-1)],

其中，rt為對數收益率，Pt為股票日收盤價。收益率序列的邊緣分布建模，M-Copula函數的參數估計以及投資組合的在險價值計算均在Matlab 2016a軟件中進行。

2.1 描述性統計

先對5只股票的對數收益率進行描述性統計，其結果如表1所示。孟買SENSEX30指數的平均收益率最大，而俄羅斯RTS指數的平均收益率最小，為負值。從標準差來看，俄羅斯RTS指數的波動最大，而富時新加坡STI指數的波動最小。另外，5只股票的偏度均小于0，峰度均大于3，這表明了金融收益率的“尖峰厚尾”性。表1數據顯示5只股票收益率的J-B檢驗的統計量的P值均≤0.05，所以均拒絕原假設, 即不服從正態分布。由于收益率不服從正態分布，因此不能運用均值方差模型來度量投資組合的風險。

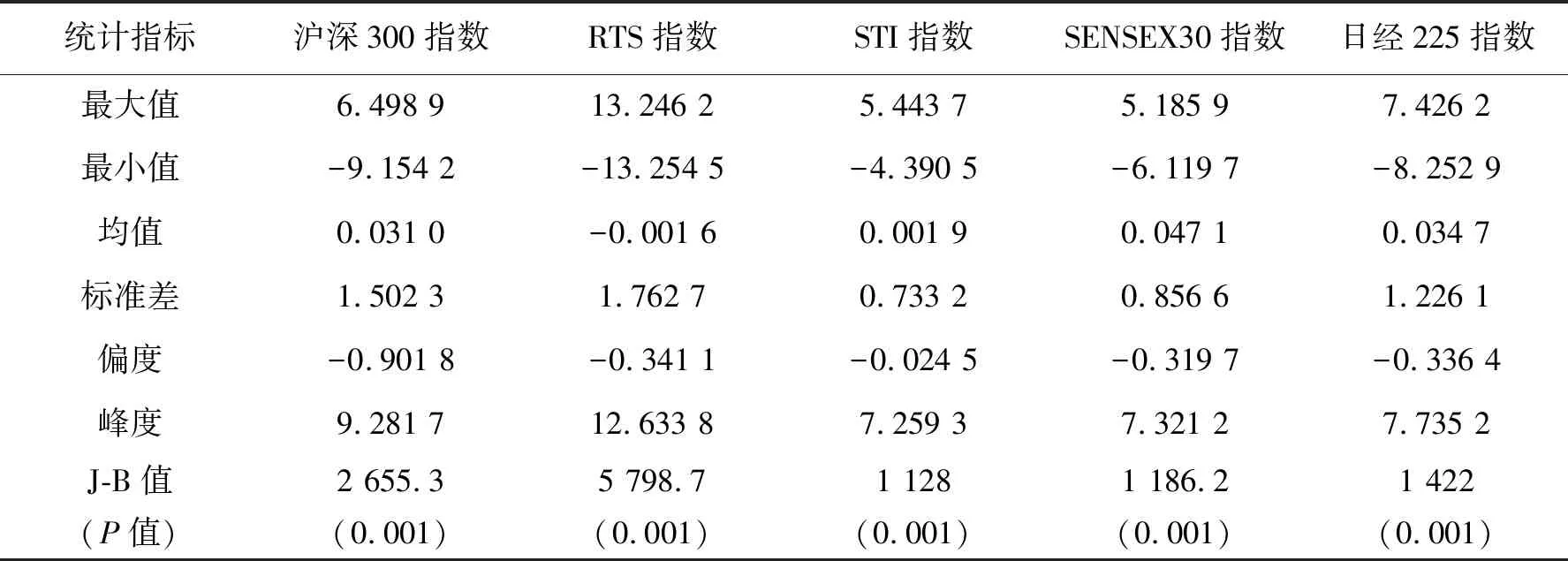
表1 股指收益率的描述性統計Tab. 1 Descriptive statistics of stock index returns

2.2 邊緣分布建模

在進行邊緣分布構建之前需要先檢驗各只股票指數的對數收益序列是否滿足GARCH建模要求。因此，首先對其進行單位根檢驗，再對其作異方差性檢驗。檢驗結果如表2所示，由ADF檢驗和PP檢驗的P值均≤0.05有各股指收益率數據不存在單位根，即為平穩的時間序列。進一步根據拉格朗日乘子檢驗(LM檢驗)方法進行異方差性檢驗，由ARCH-LM的P值均≤0.05有各收益率序列均具有ARCH效應，因此，適合用GARCH模型擬合。

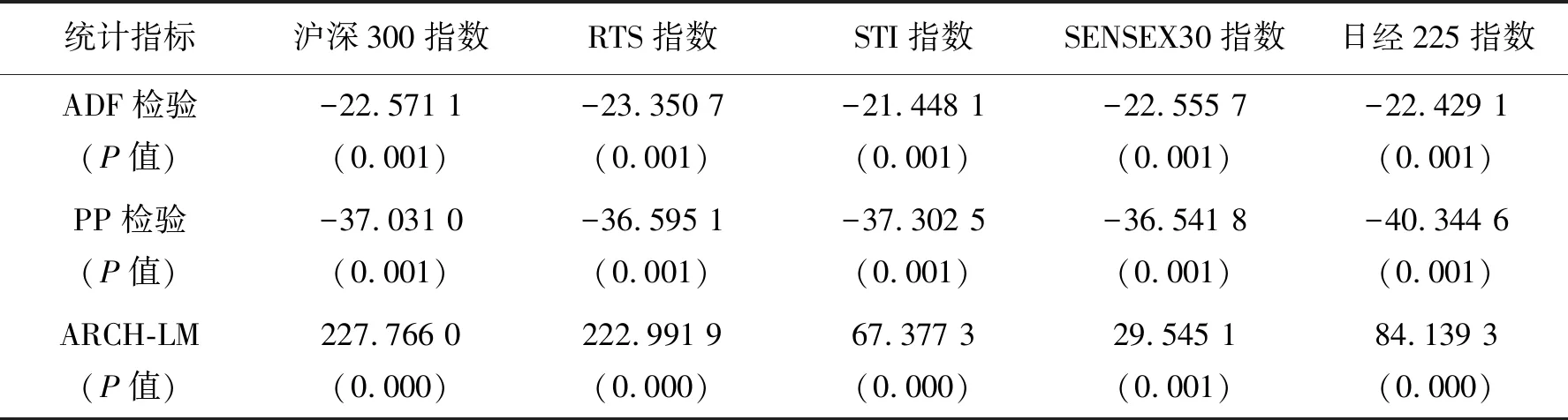
表2 股指收益率的單位根檢驗及異方差檢驗Tab. 2 Unit root test and heteroscedasticity test of stock index return rate

下面，將采用GJR-GARCH(1,1)-t模型對各對數收益率序列進行邊際建模，表3為各參數的估計結果。從表3數據可以看出，各收益率序列具有持續性波動的特點。另外，從參數γ觀察到除滬深300指數，其余四支股指均存在杠桿效應。由參數ν可知，俄羅斯RTS指數收益率序列自由度最大，出現極端事件的概率最小；相反，日經225指數收益率序列自由度最小，出現極端事件的概率最大。k-s檢驗顯示P值均>0.01，表明標準殘差經概率積分變換后為[0,1]上的均勻分布。

表3 GJR-GARCH(1,1)-t模型的參數估計Tab. 3 Parameter estimation of GJR-GARCH (1,1) -t model

2.3 M-Copula參數估計

對股指收益率的邊緣分布建模后，再對進行了概率積分變化后服從[0,1]均勻分布的殘差序列進行M-Copula模型擬合，進而研究5只股指之間的相關關系。將極大似然估計法與EM算法、BFGS算法結合起來對M-Copula函數模型進行參數估計，得到最終的權重參數ω1，ω2，ω3和各Copula相依參數θ1，θ2，θ3，其結果如表4所示。Clayton-Copula函數所占的權重最大為0.541 8，表明5只股票具有較強的下尾相關性，更可能發生同時下跌的情況；Gumbel-Copula函數所占的權重次之為0.347 6，說明5只股票之間的上尾相關性較下尾相關性弱；Frank-Copula函數的權重最小為0.110 6，表明5只股票之間的對稱相關性最弱。

表4 M-Copula函數模型的參數估計Tab. 4 Parameter estimation of M-Copula function model

2.4 VaR的計算

利用Monte Carlo模擬，隨機生成T=5 000組服從上述五維M-Copula函數的隨機向量(u1,t,u2,t,u3,t,u4,t,u5,t),t=1,2,…,T，并通過GJR-GARCH(1,1)-t模型所擬合的各收益率序列得到5只股票的模擬收益率，隨后分別計算如表5所示的3組不同權重下的投資組合的收益，最后計算在置信水平為95%和99%條件下各資產組合的風險價值VaR。

表5 投資組合的權重Tab. 5 Portfolio weight

表6顯示不同置信水平下的單一資產和資產組合的VaR，從表6中數據可以看出，就單一資產而言，日經225指數的VaR值最大，表現出日本股票市場的風險較高；RTS指數VaR值最小，表現出俄羅斯的股票市場風險較小。其次，單一資產和資產組合的VaR值均隨著置信水平的增大而增大；而在同一置信水平下，單一資產的風險要大于資產組合的風險。說明投資者可以通過有選擇性地組合資產來分散非系統性風險。3種不同投資權重的資產風險也不同，因此，權重系數的選擇對資產組合的風險有一定的影響。提醒投資者在金融投資的時候應避免只大量投資某一個股票，適當的投資組合能減小投資風險，并且在組合投資時把握好不同的投資權重以獲得更大的收益。

表6 不同置信水平下的VaR值Tab. 6 Value at risk under different confidence levels

3 總結

“一帶一路”的提出對亞洲國家的經濟發展起到了重要的促進作用。“一帶一路”沿線國家之間金融合作逐漸深入，因此對“一帶一路”沿線國家股票市場間相關結構的研究以及度量金融風險就很有必要，這既能為金融市場的共同發展提供參考，又能為投資者提供建議。本文首先使用GJR-GARCH(1,1)-t模型擬合各股指的收益率; 其次選擇M-Copula函數模型對5只股票之間的相關結構進行描述，分析了“一帶一路”沿線5個國家股票市場的相關性；最后，運用Monte Carlo模擬方法度量投資組合的風險價值。主要結論如下：

(1) 使用GJR-GARCH(1,1)-t模型來擬合單只股票收益率序列時，除滬深300指數，其余4支股指均存在杠桿效應。更加說明中國、俄羅斯、新加坡的投資者更傾向于視股票投資為高風險高回報的投資，在股票價格增長時，會更大可能性地拋售股票以此獲利；在股票價格持續走低時更傾向于繼續持有股票， 等待價格反彈。印度和日本的投資者更傾向于在股票價格持續增長時保留股票，從而使得股票波動率下降，市場平穩。

(2) 利用M-Copula函數模型研究5只股票的相關結構時，不難發現5只股票具有較強的下尾相關性，且上尾相關性較下尾相關性弱，更可能發生同時下跌的情況。表明5只股票之間的對稱相關性最弱。每個國家的經濟發展程度不同，資產組合間的相關關系在金融市場總環境的影響下，表現出來的反應程度也不一樣。 通過推動“一帶一路”在全球范圍的實施，可以穩定金融市場結構，帶動我國以及沿線國家的經濟發展。但是，在經濟全球化和“一帶一路”發展模式的影響下，一個國家的股票市場價格波動也會影響其他國家的股票價格波動，金融市場的監管部門應時刻關注全球股票市場的波動情況，嚴控風險，使得金融市場穩健運行。

(3) 在度量資產組合的風險價值時，單一資產和資產組合的在險價值VaR均隨著置信水平的增大而增大；而在同一置信水平下，單一資產的風險要大于資產組合的風險。并且，在不同的投資權重下，資產組合的風險也存在著明顯的差別。因此，投資者在金融投資時如果只考慮投資其中一種股票時，應選擇風險價值相對較小的，或者選擇適當的投資組合，以此減小投資風險。

本文的研究仍然存在著一些不足之處。刻畫股票市場之間的相關結構也可能會隨著時間的變化而變化，即Copula函數的參數是靜態不變的，這可能對刻畫相關結構時造成一定的誤差。此外，在險價值VaR有一定的局限性，不是一致性風險度量指標，即不滿足次可加性。因此，下一步的研究可以考慮結合動態Copula模型來更準確地度量資產價格的風險價值。