聚焦教材中的實驗題,讓數學變得“好玩”
吳敏強

[摘? 要] 數學實驗是研究數學的不可忽視的方法,文章以探究圓錐曲線的定義為例,利用教材課后實驗題,設計并實踐了一堂數學實驗課. 在課堂中利用數學實驗讓學生領略數學的魅力為探究,同時體現教材實驗題的巨大價值,促進學生獨立思考和創新意識的培養.
[關鍵詞] 數學實驗;教材實驗題;圓錐曲線
比對以核心素養為統領的課改訴求,當前高中數學課程和教學在“事實”、素材、問題、過程等方面都有所欠缺,出現了像中科院院士李大潛所指出的那種“長期存在的矛盾現象:一方面數學很有用,另一方面學生學了數學以后卻不會用”. 改變現狀必須從完善課程內容、加強實踐環節入手,而以“數學實驗”為載體的教學創新適逢其時.
數學實驗課,讓我們的課堂可以不再“一支筆一張紙打天下”,同時讓知識的傳輸由單方向向多方向發展. 它提高了學生在數學課堂中的參與度,當學生全身心地融入實驗中時,他們的主觀能動性會得到充分的發揮. 數學實驗會引起學生對數學知識的探究欲和學習興趣,因此,實驗課能促進學生獨立思考和創新意識的培養.
教材中有許多的實驗題,或者說是動手操作題,被許多教師忽略,其實,這些實驗題是學生體驗數學生成的絕佳材料. 筆者以探究圓錐曲線的定義為例,利用教材課后的實驗題,設計并實踐了一堂數學實驗課,課堂實錄與設計理念如下:
■復習鞏固回顧
師:同學們,今天我們一起重新探究圓錐曲線的定義,今天的探究需要我們動手動腦,我們上一堂數學實驗課.
師:圓錐曲線的形成有幾種方式?
生:可以用平面去截圓錐,不同的角度的平面會截得不同的圓錐曲線.
生:滿足一定條件的動點的軌跡.
師:兩位同學給出了兩種不同的生成方式,這是我們之前學習過的,那么還有其他的生成方式嗎?
(學生思考中)
師:其實,我們還可以通過折紙的方式生成圓錐曲線,請大家拿出我們之前準備的圓形紙片,嘗試下面的實驗
設計理念:對于一堂實驗課,明確的實驗目標可以讓學生迅速地進入實驗思考狀態,為實驗的開展指明方向. 故筆者在本課復習鞏固階段,簡明扼要地給出了實驗目標,引導學生對實驗進行思考. 同時,讓學生復習圓錐曲線的定義和生成方式,把學生帶回到“最近發展區”,為本課后續的結論驗證提供必要的理論儲備和“后勤保障”.
■動手實驗探究
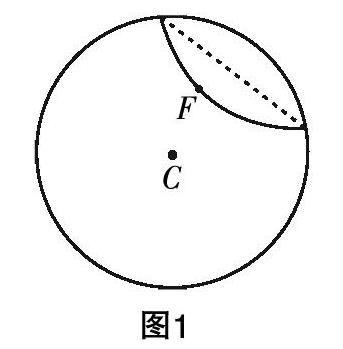
實驗1(蘇教版高中數學選修2-1):準備一張圓形紙片,在圓內任取不同于圓心C的一點F,將紙片折起,使圓周過點F(如圖1),然后將紙片展開,就得到一條折痕l(為了看清楚,可把直線l畫出來). 這樣繼續折下去,得到若干折痕. 觀察這些折痕圍成的輪廓,它是什么曲線?
(實驗活動,教師給予充足的時間)
師:哪位同學能展示一下你的實驗成果?
生:(展示實驗成果,如圖2)這些折痕圍成的輪廓很像橢圓.
設計理念:實驗課最重要的目的是讓學生在實驗操作中體驗理論的生成,故學生的實驗操作部分是本課的核心,學生的實驗體驗直接會影響學生本節課的學習興趣與動力,故筆者在課堂上對本次實驗給予了足夠的重視,給足了學生足夠的實驗操作時間,對于部分實驗有困難的學生在課堂巡視中給予適當的提示與幫助,并且盡力讓所有學生都能充分體驗,生成各自的實驗結果,充分的體驗為后續尋求理論支撐提供“養料”.
■尋求理論支撐
師:折痕圍成的輪廓一定是一個橢圓嗎?
生:不一定.
師:沒錯,這個只能是我們實驗后的一種猜想,那我們接下來應該做什么?
生:我們要證明這個輪廓是一個橢圓.
師:很好,請大家想一想,怎么證明這是一個橢圓呢?
生:我們需要證明輪廓上的任意一點都符合橢圓的定義,也就是說我們只要證明輪廓上的任意一點到兩個定點的距離之和為定值(定值小于定點間距),那么我們就可以說這個折痕輪廓就是一個橢圓了.
師:很好,那么請同學們試著證明這個結論.
(學生思考證明)
師:哪位同學能說一下想法?
生:我可以證明折痕上存在點P的軌跡是一個橢圓. 設折痕為l,那么點F關于折痕l的對稱點Q一定在圓弧上,連接CQ交l與點P,連接PF. 因為點P在折痕上,所以PF=PQ,所以PF+PC=PQ+PC=r. 又因為定點F在圓C內,所以CF 師:非常好,這位同學證明了在折痕上存在軌跡為橢圓的點. 那么問題來了,點P的軌跡是不是就是我們折痕圍成的橢圓呢? 生:老師,我能證明折痕上只有這一個點的軌跡是以C,F為焦點的橢圓,其他點的軌跡都不是橢圓P,這樣就可以說明點P的軌跡就是我們折痕圍成的橢圓了. 在折痕l上任取異于點P的點M,則MF=MQ,此時MC+MF=MC+MQ. 因為點M異于點P,故在三角形CMQ中,總有MC+MQ>CQ,即MC+MQ不是一個常數,所以點M不在橢圓P上,可見折痕和橢圓只有一個交點P,該折痕就是橢圓的一條切線. 同理,每一條折痕都是橢圓的切線,所有切線圍出的輪廓就是橢圓,我想,這就是我們能通過這個方法折出橢圓的原理. 師:非常好,通過同學們的合作探究,我們不僅折出了橢圓,還給出了證明,找到了折紙方法的原理,在實驗中體驗數學理論的生成,非常有意思! 具體證明過程給予板書演示(略). 設計理念:實驗結論最終要回到理論層面. 對實驗生成的初步結論進行科學的驗證,才是完整的實驗,未被驗證的結論只能說是猜想. 在驗證中調整實驗,在實驗中完善結論,這就是實驗課的經典模式,也是實驗課帶給學生最有價值的體驗. 邏輯推理是數學六大核心素養之一,提高學生邏輯推理能力也是數學課程的重要目標. 故本節課的第三部分“尋求理論支撐”也是本節課支撐師生互動,進行實驗結論的成功驗證. 從數學層面,是對實驗結果的理論支撐;從教學層面,既是對學生實驗的肯定,也是對學生進行后續實驗的有力支持. ■獨立實驗與探究 師:那么老師把實驗條件變一下,請同學看實驗2. 實驗2(蘇教版教科書選修2-1):在紙上畫一個圓C,在圓外任取一定點F,將紙片折起,使圓周過點F(如圖3),然后將紙片展開,就得到一條折痕l(為了看清楚,可把直線l畫出來). 這樣繼續折下去,得到若干折痕. 觀察這些折痕圍成的輪廓,它是什么曲線? 學生有了實驗1的經驗,實驗2比較順利,很快有了實驗結果,并進行了理論證明,具體過程在此不再贅述. 設計理念:縱向或橫向的拓展訓練是鞏固學習成果的一個重要手段. 那么作為實驗課,學生有了第一次完整實踐經驗后,獨立完成拓展實驗,可以有效地加固學生對實驗流程的理解,加強數學實驗與理論驗證的體驗,對于課程體驗與數學理論的內化起到重要作用. ■反思與總結 師:好的,我們同學都非常順利地完成了實驗2,并給出了證明,體驗了橢圓和雙曲線的實驗. 通過這節課,同學們可以充分地體驗到數學實驗的魅力,在實驗中探尋理論,在理論中完善實驗, 數學也可以很“好玩”. 設計理念:總結是面向過去的再學習,而反思是面向未來的再學習,總結與反思是學生自我提升的最佳方式,筆者非常重視在課堂上滲透自我反思的理念,培養學生好的學習習慣. ■課外實驗延伸 師:最后,我們知道圓錐曲線還有一種曲線——拋物線,能不能也用折紙的方法生成拋物線呢?另外,圓錐曲線還有沒有其他的生成形式呢?這兩個問題就留給大家課后思考探究! 設計理念:“教是為了不教”,由課內延伸到課外是學生發展的必經之路,筆者對這部分教學設計的目的是為了讓科學實驗探究的理念滲透到學生的日常生活中,經歷實驗的操作,學生能學會用實驗方式探究真實世界,發現和提出問題,覺察數學與現實之間的聯系;累積數學實踐的經驗,提升實踐能力,加強創新意識和科學精神. ■結語 數學實驗讓學生初步實踐數學知識的來龍去脈,以及利用數學與知識解決實際問題的全過程,而實驗的結果不僅僅是數學知識的建構和推導,它還反映了學生對數學原理、數學方法的掌握程度和數學應用的能力,因此數學實驗可以增強學生對世界的認知能力和知識應用能力. 數學實驗課一定不會曇花一現,它的產生符合教育改革的路徑,所以它是一種極具生命力和發展前景的數學課程.

