三葉片H型垂直軸風力機風振與減振研究

楊夢姚，毛璐璐，韓兆龍,b,c，周 岱,b,c，雷 航，曹 宇

(上海交通大學 a. 船舶海洋與建筑工程學院；b. 海洋工程國家重點實驗室；c. 水動力學教育部重點實驗室， 上海 200240)

風能是一種重要的能源.2018年底，我國風電累計裝機容量2.1億千瓦，占全球風電市場的三分之一以上[1].風力發電機根據轉動軸與來風方向的相對位置分為水平軸風力機和垂直軸風力機兩類.以H型風機為代表的垂直軸風力機具有產生噪聲更小、整體結構更簡單、生命周期更長、發電效率更高等特點，具有廣闊的發展前景[2].H型垂直軸風力機通常由2～6片與轉軸平行的葉片組成，其結構特征使得必有葉片會處于迎風位置，易產生離心力，主軸螺栓連接處易斷裂，葉片在風荷載的作用下易產生振動問題，抗風能力較弱[3].

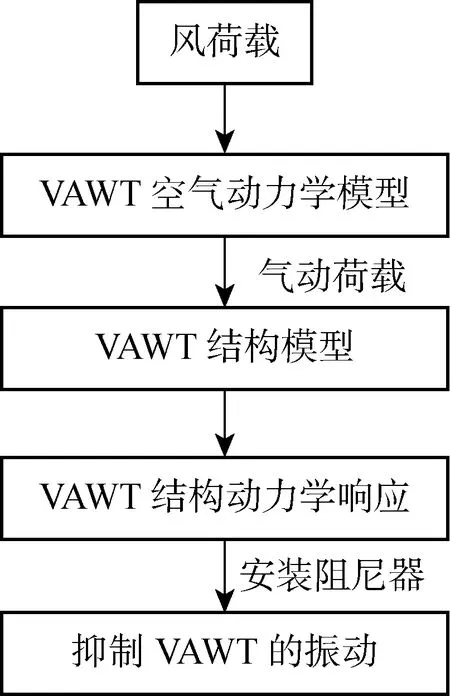
圖1 垂直軸風力機風振與減振技術路線圖Fig.1 Flowchart of wind vibration and vibration reduction of VAWT

近年來，研究者對垂直軸風機(VAWT)風振響應開展了一些研究[4-7].潘博等[8]提出研究垂直軸風機必須考慮風致振動及氣動力與葉片的共振.Campos等[9]提出結構柔度問題在風機生命周期評定中十分重要.對結構耗能減振，設置阻尼器是較為常用的方法.劉保文等[10]對大跨度斜拉橋橋塔設置縱向阻尼器，有效減小了主塔在地震荷載作用下的內力，使得內力重新分布，改善了結構受力性能.周云等[11]在某高層建筑上布置若干黏滯阻尼器，減震效果良好.目前，關于垂直軸風力機減振的研究較少.本文針對H型垂直軸風力機振動問題，在風機結構的不同位置上分別布置阻尼器，采用數值模擬的方法分析其耗能減振能力.

基于計算流體動力學，采用STAR-CCM+軟件建立垂直軸風力機的空氣動力學模型，計算風機旋轉時葉片所受氣動荷載.將氣動荷載在MATLAB軟件中進行擬合，獲得時序性風機葉片荷載函數，并將其施加到基于ANSYS軟件建立的垂直軸風力機的結構模型上，從而進行動力學分析，得到風機結構的位移響應時程.為抑制風力機的振動，在風機不同位置處施加基于COMBIN40單元而模擬的阻尼器，計算阻尼器耗能減振的能力.

1 風力機力學模型

本文的技術路線如圖1所示.H型垂直軸風力機的幾何模型如圖2所示(其中數字為節點編號)，其通常由2～6片葉片組成.目前2葉片或3葉片風機在風電市場上應用較廣[1]，茲選取典型3葉片H型垂直軸風力發電機為對象，研究風機旋轉時風荷載對風機振動穩定性的影響.垂直軸風機多采用對稱翼型，故本文中風機的葉片翼型截面選擇NACA-0021[12]，D型主梁處材料采用碳纖維，葉片蒙皮處材料采用玻璃纖維.主軸與支桿材料采用Q345鋼材[13]，彈性模量E=200 GPa，泊松比μ=0.17，密度ρ=7.8×103kg/m3.為減小計算量，選用某大型10 MW風機的100∶1縮尺模型.風機模型的幾何尺寸為：弦長C=0.265 m，支撐桿長D=0.8 m，葉片高度H=1.2 m，主軸和撐桿截面皆取圓截面，主軸直徑為0.2 m，撐桿直徑為0.1 m.

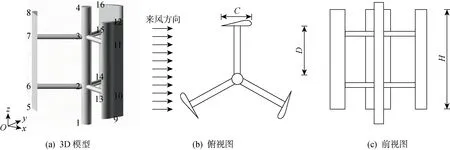
圖2 H型垂直軸風力發電機的幾何模型Fig.2 Geometric model of a H-rotor type vertical axis wind turbine

2 分析方法

2.1 風力機風荷載模擬

由于風機翼型截面的復雜性，故較難手動計算出風機表面荷載的數值.計算流體動力學方法常應用于解決流固耦合問題[14]，茲基于計算流體動力學理論開展H型垂直軸風力機葉片表面風荷載時程的數值模擬研究.采用雷諾平均(Reynolds Averaged Navier-Stokes, RANS)和標準k-ε湍流模型[15]作為數值模擬方法，運用STAR-CCM+軟件進行數值計算.雷諾平均納維-斯托克斯(N-S)方程為

(1)

式中：ui、uj分別為i、j方向的速度分量，i、j為坐標軸方向；t為時間；xi、xj為坐標；ρ為流體密度；p為壓力；ν為動力黏度系數；上標“ ′ ”代表來流的脈動值.

由于本文的研究目的側重于風機減振，所以對于風機的氣動荷載采用一些簡化計算，具體如下：① 風力機處于自然大氣邊界層中，因其葉片高度不大，故可不考慮風速梯度的影響.② 考慮到在實際工程中，近地面的湍流強度較大.且當風力機轉速恒定時，來流風速越低，風機葉尖速越大，因風輪轉動引起的湍流強度隨之增大.在這種高葉尖速比的條件下，湍流強度的大小會對風力機的氣動力造成一定影響[16].為簡化模型，本文的計算條件參考相關風洞實驗條件設置[16],其中來流風速為8 m/s，湍流度為0.005.③ 因本文的研究對象是風力機的縮尺模型(1∶100)，故本文的雷諾數是原模型的1/100，根據文獻[16]，雷諾數越大，風機的空氣動力學性能越好，同時，由于葉片升力系數的增大，轉子轉矩也更大.因此本文所采用的縮尺模型的氣動載荷特性與原模型存在一定的偏差，模型的折算氣動載荷略小于實際載荷.④ 在CFD數值模擬過程中，為簡化計算，未考慮葉片結構變形的影響.

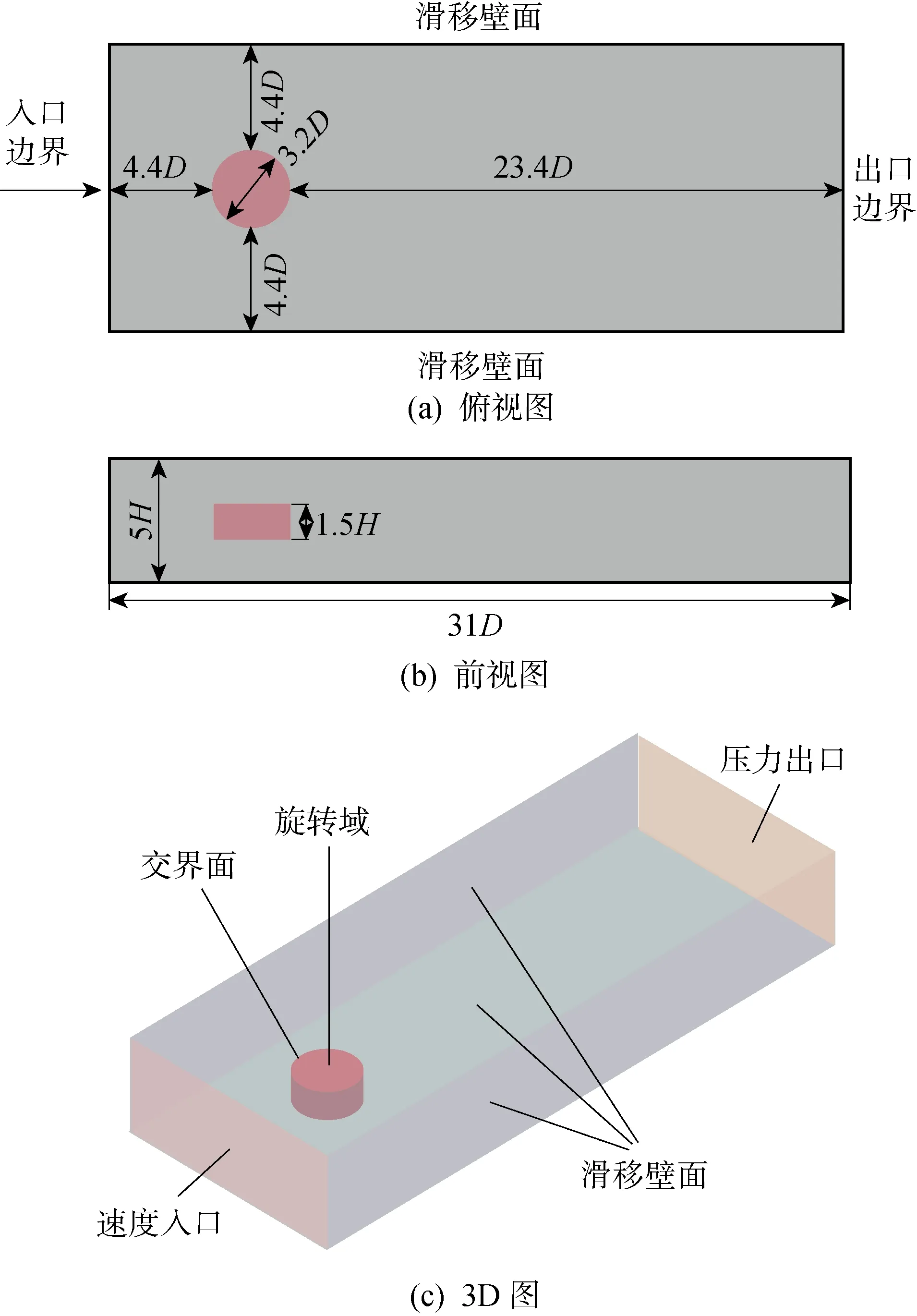
圖3 風場計算域與邊界條件Fig.3 Calculation domain and boundary conditions of wind field

為減少邊界條件的影響，在選取風場計算域時，取其尺寸為31D×12D×5H[17]即24.8 m×9.6 m×6 m.將垂直軸風機的中心置于計算域的前1/3處，以確保計算域風場流動發展完全，如圖3所示.入口選用速度邊界條件，計算風速取8 m/s；出口選用自由擴展邊界條件；風輪區域流體定義為旋轉流體，風輪定義為相對旋轉固體壁面；壁面選用滑移壁面.對風場計算域進行網格劃分，使近葉片周圍的網格較密集，遠離葉片的網格較稀疏.由此共劃得棱柱形網格約1.89×106個，風場計算域的阻塞率小于3%，無量綱化的壁面距離y+<1，滿足數值模擬對于網格的要求[18].

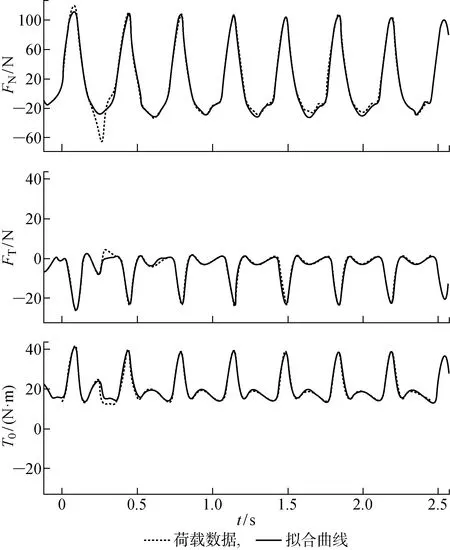
圖4 葉片氣動荷載時程曲線與函數擬合結果對比Fig.4 Comparison of blade aerodynamic load time history curve and function fitting results

本文計算得到葉片的轉矩荷載時程曲線結果如圖4所示.圖中：T0為轉矩，FT為切向力，FN為法向力.將其與Lei等[19]的轉矩時程曲線進行對比，發現具有相同的波形且荷載數值接近.

由于風機的氣動荷載呈現周期性，所以可采用周期函數對其進行擬合.在MATLAB中，采用多階正弦函數對風機的切向力、法向力及轉矩時程曲線進行擬合，獲得相應的荷載函數,便于在ANSYS中對結構進行瞬態分析.以葉片的法向力為例，任一時間序列的荷載函數可近似模擬為

(2)

式中：fn(t)為t時間下的葉片法向力；ai、bi及ci分別為第i個正弦函數的各項系數.

如圖4所示，法向力、切向力及轉矩的荷載函數曲線的擬合效果較好，幾乎與氣動荷載時程曲線保持一致.因此，采用多階正弦函數對氣動荷載數據進行擬合的方法是可行的.

2.2 結構風致振動響應分析

運用ANSYS/Mechanical APDL 18.2軟件開展有限元數值模擬研究，采用Newmark-β方法進行瞬態分析.Newmark-β方法是一種隱式時間積分方案，具有二階時間精度[20]，此處選取γ=0.5，β=0.25(γ和β分別為控制數值分析精度和穩定性的參數)，即平均常加速度法.邊界約束條件為底端固接，在葉片表面施加氣動荷載，用四面體型三維實體單元對模型進行網格劃分，共得到5.234×104個網格單元.圖5為葉片表面所施加的荷載示意圖.

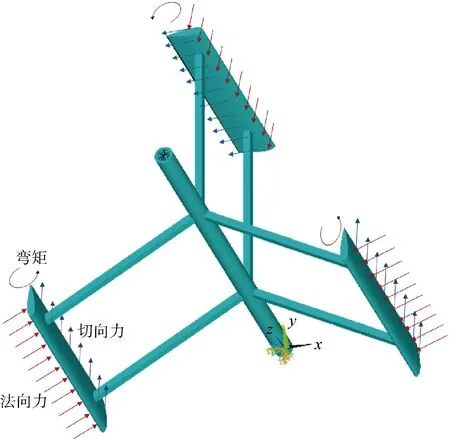
圖5 葉片施加荷載示意圖Fig.5 Schematic diagram of blade loading

風機結構在荷載激勵下的運動方程可以表示為

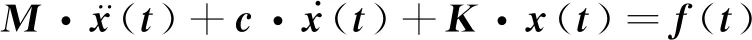
(3)

用有限元方法求解上述方程，可以得到各節點的風致響應.

2.3 阻尼器模擬

在建筑物或空間結構上安裝單個或多個阻尼器，可以抑制結構的振動響應[21-22].阻尼器會隨著風機的振動而振動，其產生的慣性力作用可部分抵消風荷載對風機所產生的力作用，從而減小振動水平.為驗證阻尼器在垂直軸風力機上的減振性能，在原結構(模型1)的主軸與支桿連接處，即節點2和節點3處分別增加1個阻尼器，得到模型2和模型3，如圖6(a)、(b)所示.

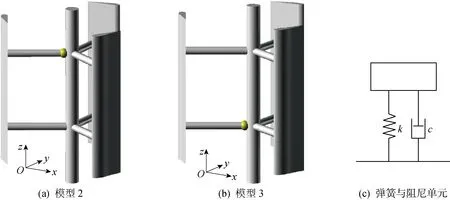
圖6 加阻尼器后風力機模型示意圖與彈簧-阻尼單元Fig.6 VAWT model with dampers and spring-damping unit

本文參考文獻[23]，采用多維減振阻尼器，它是6個自由度的并聯機構，由法蘭盤、連接耳板及阻尼元件3部分組成.其阻尼原件主要是由6個黏彈性阻尼單元構成的，在ANSYS軟件中，將其簡化為3個一維軸向COMBIN40 單元，提供三向平動自由度.3個一維轉動COMBIN40單元提供三向轉動自由度[23].COMBIN40單元是由相互平行的彈簧滑動器和阻尼器組成，并且串聯著一個間隙控制器的彈簧單元.在本文的計算中，將其簡化為相互平行的彈簧和阻尼器單元，如圖6(c)所示，其中k為彈簧剛度，c為阻尼系數.

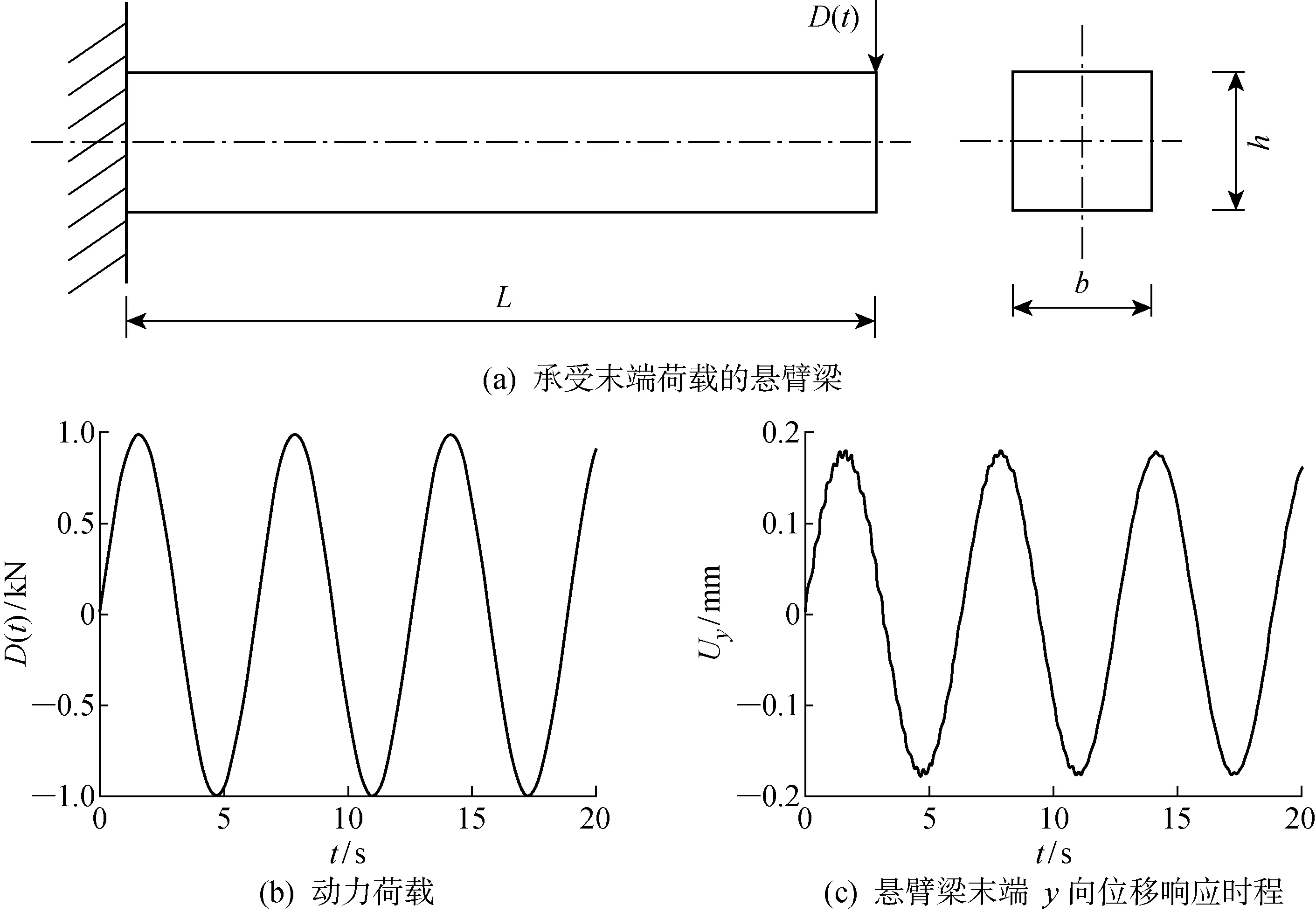
圖7 懸臂梁受動力荷載的時程響應Fig.7 Time-history response of cantilever beam at dynamic load

阻尼元件的剛度和阻尼系數對于減振效果的影響非常明顯.具體體現為：當阻尼元件剛度不變時，峰值位移在整體范圍內隨著阻尼系數的增大而減小，當剛度足夠大時，阻尼系數的改變對峰值位移的影響不大.當阻尼系數不變時，峰值位移在整體范圍內隨著剛度的增大而減小，當阻尼系數足夠大時，剛度的改變對峰值位移的影響不大.基于上述規律并經過反復試算，最終假定阻尼元件剛度為5×107N/m，阻尼系數為2.5×107N/(m·s).

3 數值算例驗證

3.1 動力作用下懸臂梁變形驗證

在結構力學中，二維懸臂梁問題既是經典問題也是基準問題，被廣泛用于驗證或測試研究者提出的各種數值方法.為驗證本文方法的可靠性，考慮了在簡諧荷載作用下的懸臂梁變形問題.問題定義及荷載曲線如圖7(a)、(b)所示.懸臂梁的長度L=10 m，梁截面寬度b=1 m，高度h=1 m，彈性模量E=2.3×1010Pa，泊松比μ=0.27.在懸臂梁自由端施加簡諧荷載D(t)，荷載函數為D(t)=1 000sint，如圖7(b)所示.計算所得最大位移為0.177 mm，如圖7(c)所示，圖中Uy為懸臂梁末端y向位移時程，與文獻結果[24]對比，響應幅值與響應頻率與文獻結果相符.

3.2 時間步長選取

對于運用ANSYS分析瞬態動力學問題，選取不同的時間步長和時間步會對結果產生影響.時間步長越小，計算精度越高，但相應會造成計算資源的浪費，因此在數值模擬前應當先選取合適的時間步長.茲對計算模型進行在3種時間步長下的模擬，即：0.004、0.002及0.001 s，分別得到對應的結構關于x軸的底部彎矩M0(見表1)：

(4)

式中:hi為結構物的高度；P(x)為x高度處結構表面壓力；A，Ai為受力面積.

表1 不同時間步長下底部彎矩比較

從表1看出，當時間步長為0.002 s時，Mx為107.47 N·m，與時間步長取0.001 s時所得的結果相差僅0.7%，可看作近似相等.故時間步長為0.002 s時，既能保證所得結果的精確性，也能節省計算資源.茲選取時間步長為0.002 s.

4 數值結果與分析

4.1 風荷載模擬

本文僅考慮來流風速8 m/s，風機轉子轉速17.92 rad/s[19]的工況下，垂直軸風機所承受的氣動荷載.風機旋轉1個周期所需的時間 0.350 6 s.圖8所示為第6個周期計算結束即t=2.103 6 s時其中1個葉片的壓力(p′)分布，圖中坐標系為葉片的局部坐標系.結果表明：較大的正壓力出現在葉片翼型前緣，與文獻結果相符[25].圖4所示為葉片上的瞬時風壓隨時間的變化趨勢.可見，在前兩個周期內，相鄰周期的壓力峰值差距較大，在風機旋轉了2～3個周期之后，壓力數值趨于穩定.

圖8 風機葉片壓力云圖Fig.8 Pressure cloud diagram of fan blade

4.2 風機結構的風致響應分析

在運用ANSYS軟件計算垂直軸風力機的振動響應時，由于垂直軸風力機旋轉過程中葉片的氣動荷載隨時間呈周期性變化，所以，將周期性變化的氣動荷載加載到風機結構上，即是把原來的風載恒定，風機轉動的問題轉化成了風機不動，而風載隨時間變化，從而計算風機的振動響應.在風機結構響應分析中，為簡化計算，未考慮結構整體轉動的自由度.同時，本文中未考慮風機轉動對風振響應的影響，風機轉動可能會使風機的風振響應更為復雜，在后續研究中將進一步展開分析.

分析發現t=10 s時，結構的振動幅值較大，故選取t=10 s時刻下的總位移云圖分析，如圖9所示,
圖中Usum為風力機結構的總位移.圖9(a)所示為t=10 s時，原結構(模型1)的總位移云圖.可見，模型1的最大位移發生在位于葉片頂端的節點16處，達到2.7 mm.即在該時刻下，風機的危險點為節點16，由于風機葉片的對稱性，可重點關注葉片頂端節點.圖9(b)所示為t=10 s時，在上部支撐桿處加了阻尼器后的模型2總位移圖，此時最大位移發生在位于葉片底端的節點9處，數值為1.5 mm，下降達44.4%.圖9(c)所示為t=10 s時，在下部支撐桿處加了阻尼器后模型3的總位移圖，此時最大位移仍舊發生在位于葉片頂端，數值為1.6 mm，下降達40.7%.

為更清晰地對比結構的三向位移，用圖10表示t=10 s時3個模型在x、y及z向的位移云圖，其中，Ux、Uy及Uz分別對應模型在x、y及z向的位移.由圖10對比x向位移數值，可見模型1的Ux分布在-2.7～1.0 mm，模型2的Ux分布在-0.5～0.8 mm，模型3的Ux分布在-0.9～0.9 mm，位移最大值全部發生在葉片頂端或底端.對比y向位移數值，可見模型1的Uy分布在-1.5～2.0 mm，模型2的Uy分布在-0.4～1.2 mm，模型3的Uy分布在-0.5～1.4 mm.對比z向位移數值，可見模型1的Uz分布在-0.13～0.25 mm，模型2的Uz分布在-0.04～0.04 mm，模型3的Uz分布在-0.05～0.05 mm.3個結構的x向和y向的位移數值較大且處于同一數量級，z向位移較小.

圖9 不同垂直軸風力機模型總位移云圖對比Fig.9 Comparison of total displacement contour map of different VAWT models

圖10 風力機結構三向位移云圖對比Fig.10 Comparison of three-way displacement contour maps of VAWT

由以上分析可知，原模型危險點出現在葉片頂端，故取節點8為對象，研究3個模型在風機葉片頂端的風致響應.又因x、y向位移數值較大，z向位移較小，故僅對比節點8的x、y向位移響應.圖11所示為3個模型節點8的風致響應對比.圖中Ux，8表示風力機節點8在x方向的位移，Uy,8表示風力機節點8在y方向的位移.可見，模型2和模型3在葉片頂端節點的位移抑制效果較為顯著.表2所示為3個模型的節點8的三向位移改善率統計數據.可見，模型2在x方向的平均位移改善率約為44%，在y方向的平均位移改善率約為54%，在z方向的平均位移改善率約為5%.模型3在x方向的平均位移改善率約為40%，y方向的平均位移改善率約為53%，但在z方向未見明顯改善.

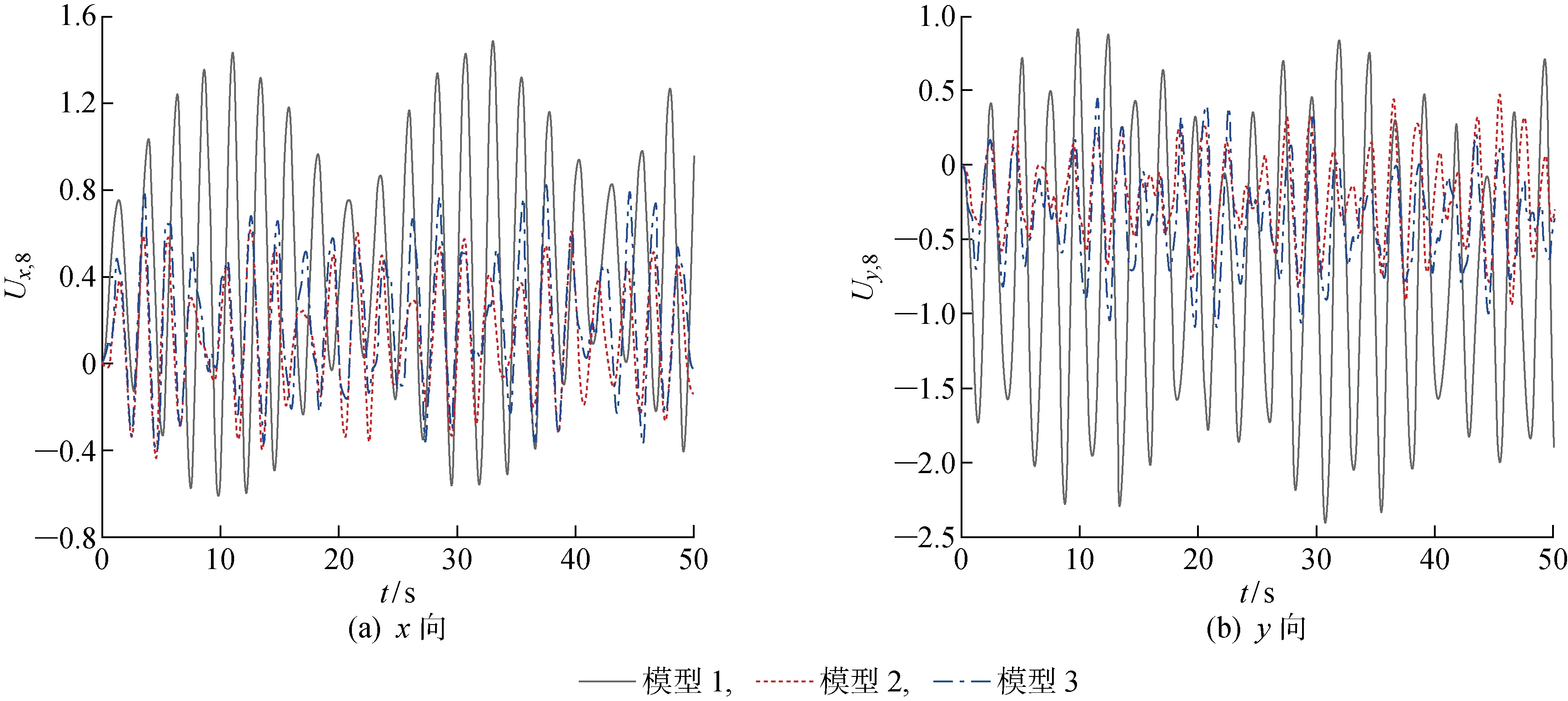
圖11 3個模型節點8的風致響應對比Fig.11 Comparison of wind-induced response of three models at node 8

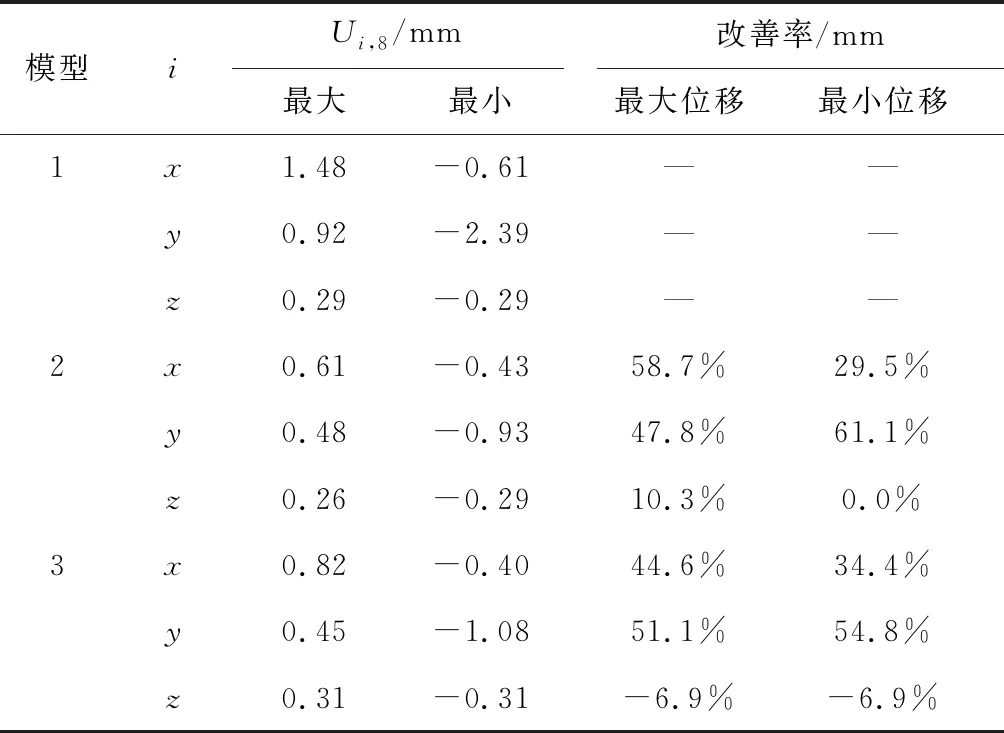
表2 3個模型節點8的三向風致響應統計

5 結論

本文針對H型垂直軸風力機振動問題，基于計算流體動力學方法，運用STAR-CCM+軟件數值模擬風機旋轉時葉片所受氣動荷載，將氣動荷載在MATLAB軟件中實施函數擬合，獲得時序性風機葉片荷載函數，再基于ANSYS軟件開展時程分析，得到風機結構的三向位移響應時程.在風機不同位置處施加基于COMBIN40單元而模擬的阻尼器，數值模擬計算其耗能減振能力.主要結論如下：

(1) H型垂直軸風力機的風致位移響應曲線具有一定的周期性.t=10 s時，風機最大位移出現在葉片的頂端，風致x、y向位移處于同一數量級，z向位移較小.

(2) 在H型垂直軸風力機的主軸與支桿連接處布置阻尼器可降低結構位移響應，總位移最大降幅達44%.

(3) 阻尼器布置的位置與結構的位移改變密切相關.t=10 s時，在近風機葉片頂端連桿處布置阻尼器，結構最大位移出現在風機葉片底端，位移下降達44%；在近風機葉片底端連桿處布置阻尼器，最大位移則依舊出現在了風機葉片頂端，位移下降達40.7%.

本文成果可為垂直軸風力機減振研究提供一定的技術參考.