微結構梯度能表面振動液滴的運動特性

熊雪嬌，賈志海，鄧 勇，費媛媛

(上海理工大學 能源與動力工程學院， 上海 200093)

疏水和超疏水表面以其較大接觸角和較小接觸角的滯后特征在化工、能源、電力等領域獲得了廣泛應用[1].如何在工程中有效利用這些表面，進而對液滴運動進行操控也由此成為近年來的研究重點.

目前，在固體表面上操控液滴產生定向運動的方式主要有兩種.① 改變表面上的微觀結構以及幾何參數[2-4]，如利用梯度能微結構表面進行液滴自推進[5-6]，所采用的梯度能表面結構主要有微柱狀[7]、微孔狀[8]、條帶狀[9]、球狀[10]等.然而，這種單純利用梯度能表面的方法并不能實現液滴的快速移動.② 利用外部刺激的方法促進液滴快速移動，采用的刺激方法主要有高溫脈沖法[11-13]、電場法[14-15]、光化學法[16]、機械振動法[17-19]等.然而，如何有效地操控液滴運動，目前仍沒有一定成法，許多方法仍處于探討之中.

近些年來，疏水和超疏水表面在滴狀冷凝傳熱研究中獲得了廣泛關注.然而，由于蒸汽冷凝形成的液滴呈現Wenzel狀態，黏附力很大，冷凝液滴往往需要生長到很大尺寸才能在重力的作用下自然脫落，使得冷凝傳熱性能不能獲得大幅提高，在蒸汽負荷較低的情況下尤其如此.所以，尋求快速的冷凝液滴脫落方法就顯得至關重要.為了探討該問題，本文嘗試設計一種新型的微結構梯度能表面，并通過施加外部機械振動研究液滴在微結構梯度表面的運動特征，并在此基礎上分析表面微觀結構對液滴運動特性的影響.本研究對梯度能表面的工程應用以及浸潤動力學理論的發展具有重要意義.

1 實驗材料及方法

選用聚二甲基硅氧烷(PDMS)，采用光刻蝕技術構筑微方柱狀拓撲結構.所制備的微方柱結構梯度能表面如圖1(a)所示.其中：l為微方柱邊長，最小微方柱邊長為30 μm，相鄰微方柱邊長以4 μm依次遞增；b=100 μm為相鄰柱間距；微方柱的高度為60 μm；c=571 μm為相鄰柱的距離.為了便于分析表面微觀結構參數對振動液滴動態行為的影響，將表面劃分為兩個區域，微方柱邊長l=30～294 μm的區域定義為I區(由接觸角測量儀測定該區域的表觀接觸角θ=105°～118°)，微方柱邊長l=298～566 μm的區域定義為 II 區(由接觸角測量儀測定該區域的θ=118°～137°).液滴表觀接觸角與表面面積分數α的關系為α=l2/(lc+bc)，如圖1(b)所示.由圖1(b)可知，液滴表觀接觸角隨著面積分數的增大而增大，且隨著面積分數的增大，其增大幅度呈逐漸增大的趨勢.

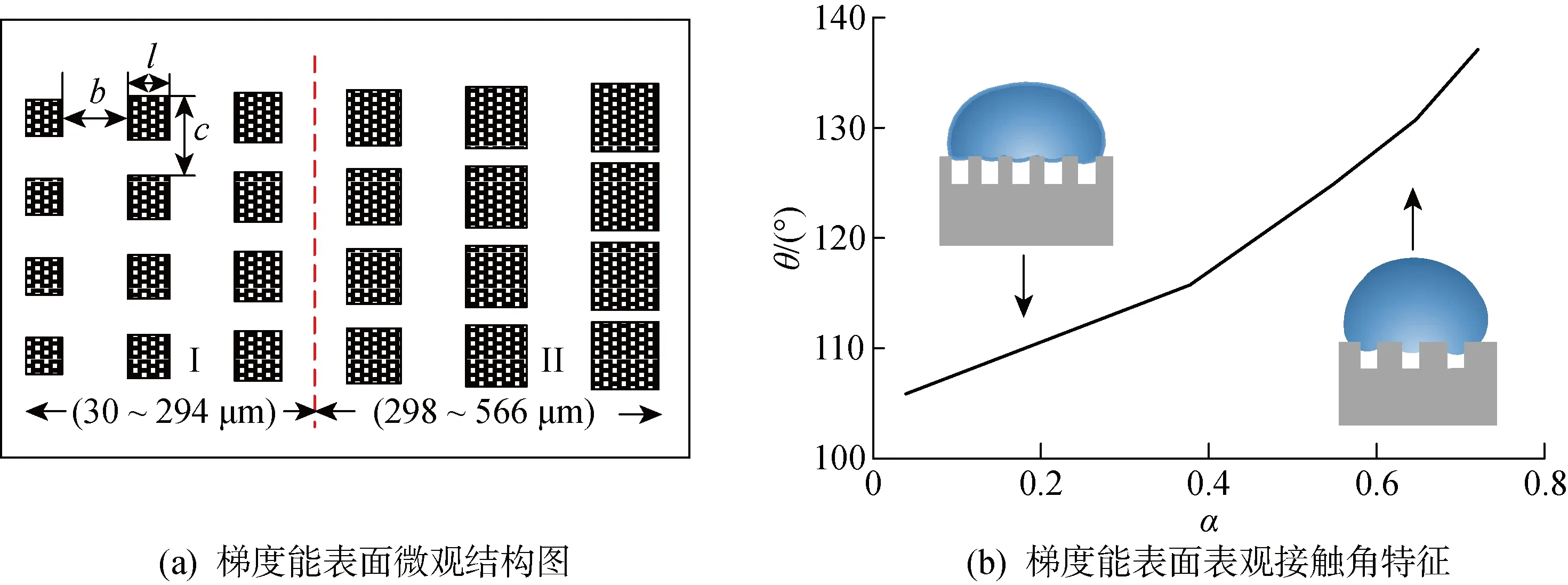
圖1 梯度能表面微結構及表觀接觸角特征Fig.1 Schematic diagram of gradient energy surface with micropillared structure and its contact angles

實驗裝置如圖2所示.采用平面喇叭振動膜產生的垂直機械振動作為振動源，振動頻率為0～200 Hz，振幅為±2 mm.利用信號發生器和功率放大器調節振動頻率和振幅，產生的正弦振動傳導至液滴.采用高速攝像儀(Fastec Imaging Hispec 3)進行圖像采集，采集速度為 1 000 幀/s.介質采用去離子水，實驗室環境約為25 ℃，相對濕度在65%左右.

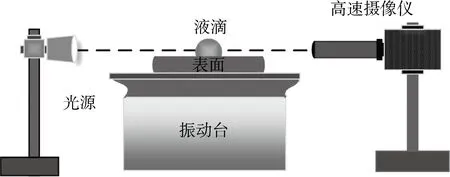
圖2 實驗裝置Fig.2 Experimental setup

2 結果與分析

當對微結構表面施加的振動頻率與液滴的固有頻率一致時，兩者會產生共振，此時振動臺向液滴傳遞能量的效率最高.因此，本實驗中施加的振動頻率均為該尺寸液滴的固有頻率.

液滴的固有頻率fn為[20]

(1)

式中：ρ為液滴密度；γ為液滴表面張力；j為引發液滴的振動模式數；V為液滴體積.

固體表面的振動液滴主要存在兩種形變模式[21]，即接觸線固定模式和接觸線移動模式.對于接觸線移動模式一般存在兩種情況(k=1或k=2，k為液滴初始狀態與運動狀態下兩者輪廓線交點個數的一半)，則有：

(2)

液滴的三相接觸線隨振動不斷變化.此時，液滴在振動模式下的節點數均為2，即k=1.由式(2)可知，j=k+1/2=3/2，進一步可通過計算獲得液滴的理論固有頻率.

將一個體積為12 μL、固有頻率約為40 Hz的液滴輕輕沉積在微結構表面上.當對其施加40 Hz的外界振動并調節其振幅時，液滴不斷產生彈性形變，但液滴的位置仍維持在原地不動.然而當振幅增加到一定閾值時，液滴雖不會脫離微結構表面，但會以蠕動的方式由面積分數較大的區域向面積分數較小的區域(從表觀接觸角較大的區域向表觀接觸角較小的區域)定向前進.液滴在區域I和區域 II 的蠕動前進特征如圖3所示.

由圖3可知，在振動過程中，液滴的濕接觸直徑d不斷變化.為了表征液滴濕接觸直徑的變化特征，引入無量綱濕接觸直徑d*(d*=d/d0，d0為液滴初始狀態的濕接觸直徑).d*隨液滴運動時間t的變化情況如圖4所示.結合圖3和4可以看到，在振動初始階段，液滴的接觸角急劇減小，無量綱濕接觸直徑突然增大，這是由于加載振動后液滴由Cassie狀態向Wenzel狀態轉變的緣故.此后，液滴向面積分數減小的方向蠕動，由于表面表觀接觸角逐漸減小，液滴和表面的浸潤程度增大，所以無量綱濕接觸直徑呈逐漸增大的趨勢.此外，液滴在蠕動過程中，d*隨著振動不斷收縮和延展，且隨時間呈波動變化.隨著振幅的增加，d*逐漸增大，液滴的形變程度加劇.對比I區和 II 區可以發現，隨著振幅的增大，II 區的d*比I區要大.這是因為當振動能量增加時，液滴在豎直方向的形變更加劇烈，無量綱濕接觸直徑增大，同時在面積分數較大的區域，液滴的表觀接觸角增大，液滴和表面之間的初始濕接觸直徑較小的緣故.

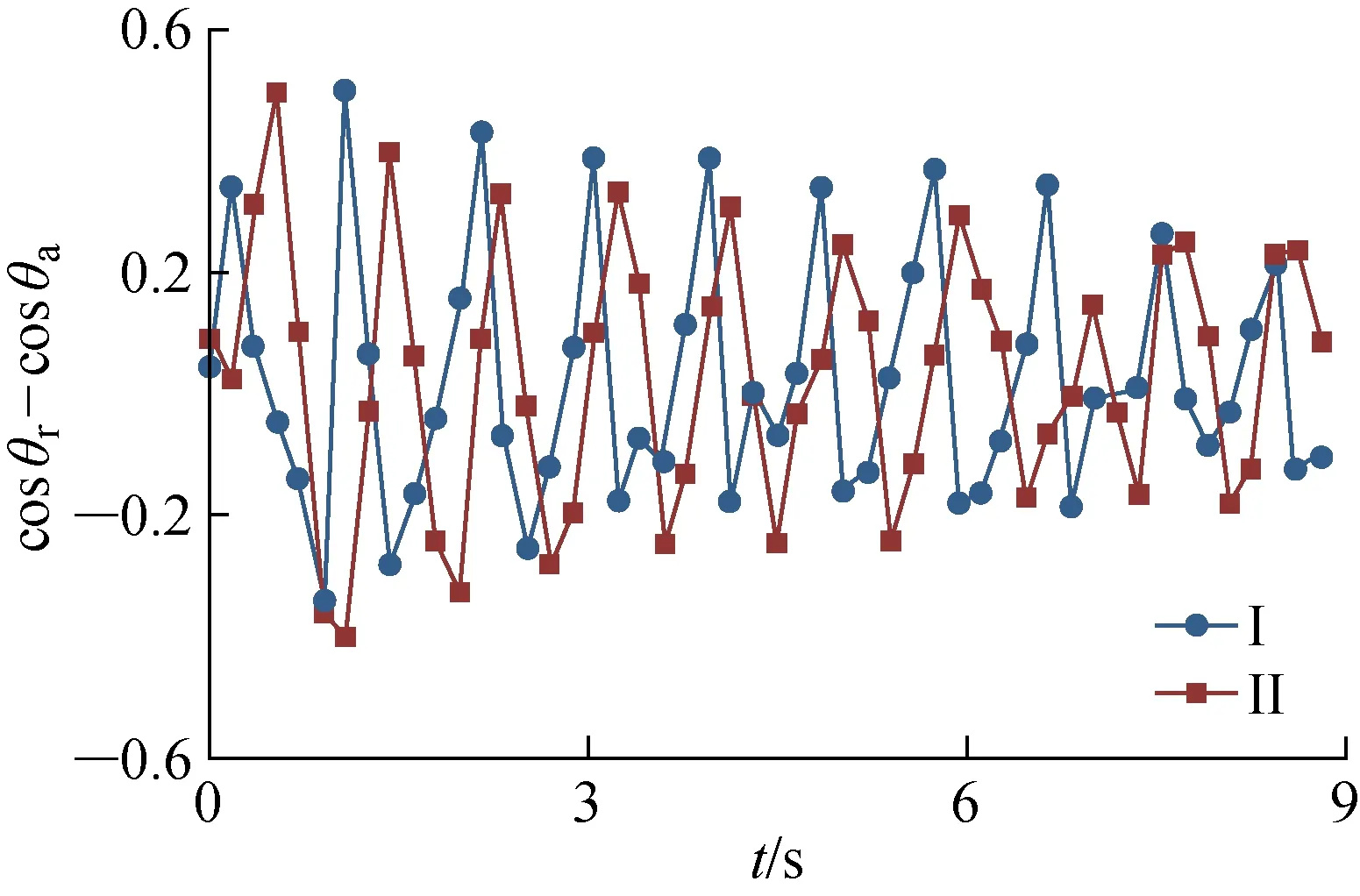
圖5 振動液滴滯后力的方向特征 Fig.5 Directional characteristics of vibrated droplets produced by hysteresis force

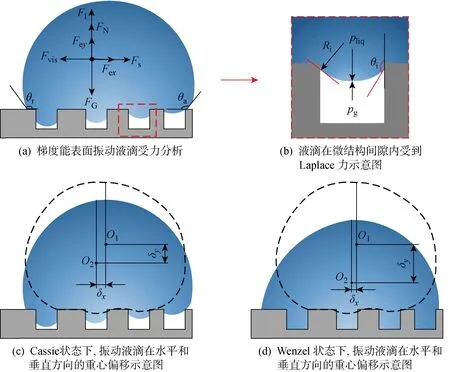
圖6 梯度能表面振動液滴受力分析圖Fig.6 Force analysis of gradient energy surface of vibrated droplets

根據Furmidge[22]研究， 液滴前進角余弦cosθa與液滴后退角余弦cosθr的差值反映了在水平方向由液滴接觸角滯后產生的滯后力方向，其變化特征如圖5所示.由圖5可見，振動過程中由于滯后引起的作用力并非一直為液滴的驅動力，有時也會成為阻力.這是因為在液滴振動過程中，液滴的搖擺使得其前進角并非一直大于后退角，進而使得力的方向發生了改變.當液滴由于滯后引起的作用力和彈性形變引起的力方向一致，前進方向上的合力能夠克服阻力時，液滴將會產生蠕動.此外，隨著液滴向面積分數較小的方向蠕動，液滴的前進角和后退角逐漸接近，由滯后引起的作用力逐漸較小，水平方向引起的彈性力也逐漸減小，最終液滴停止蠕動.

對于初始輕輕沉積在微結構梯度能表面的液滴，液滴呈Cassie狀態，液滴底部不同程度地侵入到微方柱間隙內，由此在液滴覆蓋的每個間隙內均受到Laplace力的作用，如圖6(a)所示.其中：Fex為液滴在水平方向產生彈性形變力；Fs為水平方向的作用力；Fvis為水平方向的黏附力；FG為液滴受到重力；FN為表面的支持力；FI為振動產生的慣性力；Fey為垂直方向上的彈性力.隨著面積分數的減小，底部侵入到微方柱間隙內的深度減小，曲率半徑增大，導致間隙內產生的Laplace力逐漸減小，間隙內的Laplace力如圖6(b)所示.其中：Ri為陷入微柱之間液體的曲率半徑；pliq為液體的Laplace壓力；pg為氣體的Laplace壓力;θi為陷入微柱的液體的接觸角.在這些力的作用下，液滴的重心產生偏移，引起液滴在水平方向產生彈性形變力Fex，進而造成液滴的前進角和后退角產生變化，即液滴水平方向的接觸角滯后，并由此產生水平方向的作用力Fs.當液滴產生運動后，液滴受到水平方向的黏附力Fvis.同時，在垂直方向上，液滴受到重力FG，表面的支持力FN以及振動產生的慣性力FI.此外，由于液滴的重心發生了變化，液滴受到垂直方向上的彈性力Fey.在振動作用下，初始階段液滴將由Cassie狀態向Wenzel狀態進行轉變，液滴底部受到的Laplace力逐漸消失，液滴形變程度變緩，水平方向重心偏移程度減小，縱向偏移程度增大，如圖6(c)和6(d)所示.其中：δx為液滴形變前后質心在水平方向的形變量；δy為液滴形變前后質心在垂直方向的形變量；O1為液滴形變前重心的位置；O2為液滴形變后重心的位置.

由圖6(b)可知，對于初始沉積在表面的液滴，其陷入微柱之間液體和空氣之間的Laplace壓力差可表示為

(3)

式中：γL為液體的表面張力.隨著液滴向面積分數減小的方向運動，液滴逐漸侵入到微結構間隙內，曲率半徑Ri逐漸增大，間隙內產生的Laplace力Δpi逐漸減小，因此液滴在水平方向的形變程度減小，即液滴在形變過程中表面積變化量ΔS和液滴形變前后質心在水平方向的形變量δx減小，液滴的前進角θa和后退角θr逐漸接近.需要說明的是，隨著振動過程中液滴發生向Wenzel狀態的轉變，底部間隙內的Laplace力消失，液滴只是在微結構表面的梯度表面能E作用下產生形變，其形變程度要比液滴發生浸潤狀態轉變前有所減小，導致所受到的水平方向的驅動力也隨之減小.

由振動臺傳導的能量引起的慣性力FI為

FI=ρVAf2

(4)

式中：A為振動幅值；f為振動頻率.

液滴在振動過程中因形變而產生的垂直方向上的彈性力為

(5)

形變液滴的表面能變化量可表示為

ΔE=γlgΔS

(6)

式中：γlg為氣液表面張力.根據式(5)和(6)可以推導出垂直方向上的彈性力Fey為

(7)

則液滴受到微結構表面的支持力FN為

FN=FG-Fey-FI

(8)

液滴在振動過程中因形變而產生的水平方向上的彈性力為

(9)

由液滴形變產生的水平方向上的作用力Fs[22]可以表示為

Fs=ψdγlg(cosθr-cosθa)

(10)

式中：ψ為滯留力系數，可由實驗獲取.

液滴在運動過程中受到的水平方向的黏附力Fvis為

Fvis=μFN

(11)

式中：μ為摩擦因數.將式 (8) 代入式 (11)，則有：

(12)

式中：g為重力加速度.

則液滴在水平方向的合力ΣF(以液滴向面積分數減小的運動方向為正方向)可表示為

ΣF=Fs+Fex-Fvis

(13)

將式(9)～(11)分別代入式(13)，可得

(14)

則水平方向液滴的加速度a為

(15)

式中：m為液滴質量.

根據式(14)可知，由于振動液滴的滯后力可正可負，水平方向的彈性力也可正可負，所以作用于液滴的合力也可正可負.在液滴振動的初始階段，由于梯度表面能的作用，液滴的前進角大于后退角，滯后力大于0，且液滴水平方向形變大于0，所以水平方向的彈性力為正，導致最終作用于液滴的初始合力 ΣF>0，液滴開始以一定速度向正向開始運動.然而隨著振動的進行，液滴受到的合力方向不斷發生改變，導致液滴的運動速度呈波動變化.此外，隨著液滴向面積分數減小的方向運動，振動液滴的形變程度逐漸減弱，液滴前進角和后退角逐漸接近，即(cosθr-cosθa)波動總體減小(見圖5)，液滴表面積的變化量以及水平方向的彈性形變也逐漸減小，導致水平方向上的作用力減小，水平方向的彈性力也隨之減小.在垂直方向，液滴形變程度增大，無量綱濕接觸直徑增大(見圖4)，使得垂直方向的彈性形變增大，引起垂直方向上的彈性力減小，導致支持力增大，水平方向的黏附力增大，液滴在水平方向的合力減小，液滴加速度減小直至為0.采用式(15)進行計算，獲得的理論計算結果如圖7所示.

通過高速攝影儀采集到的實驗圖片可以獲得振動液滴的運動時間，使用圖像處理技術可以獲得振動液滴的運動距離，由二者可計算出液滴運動過程中的速度，進而計算振動液滴的加速度(實驗采用的振動頻率為40 Hz，對應周期為25 ms，在加速度計算中圖片之間的時間間隔為8個周期，即200 ms).由圖7可以看到，液滴的加速度隨振幅的增大呈遞減趨勢.在振動初始階段，加速度劇烈下降而后逐漸平穩.這是因為初始時，沉積在表面的液滴呈Cassie狀態，液滴受到底部的Laplace力的作用，使得液滴變形程度增加，前進角和后退角差異顯著，導致水平方向的推動力增大，所以初始階段的加速度較大.隨后液滴在振動的作用下，發生由Cassie狀態向Wenzel狀態的轉變，液滴底部受到的Laplace力消失，液滴的形變因此減弱.隨著液滴向面積分數減小的方向運動，液滴的前進角和后退角逐漸趨近相同，水平方向的驅動力減小，加速度也隨之減小.此外，I區的加速度比 II 區大，這是因為在I區，表觀接觸角的變化幅度較大，即底部受到的表面能梯度較大，液滴形變程度較大的緣故.根據圖7的計算結果，理論模型值和實驗結果吻合良好，從而驗證了模型的正確性.

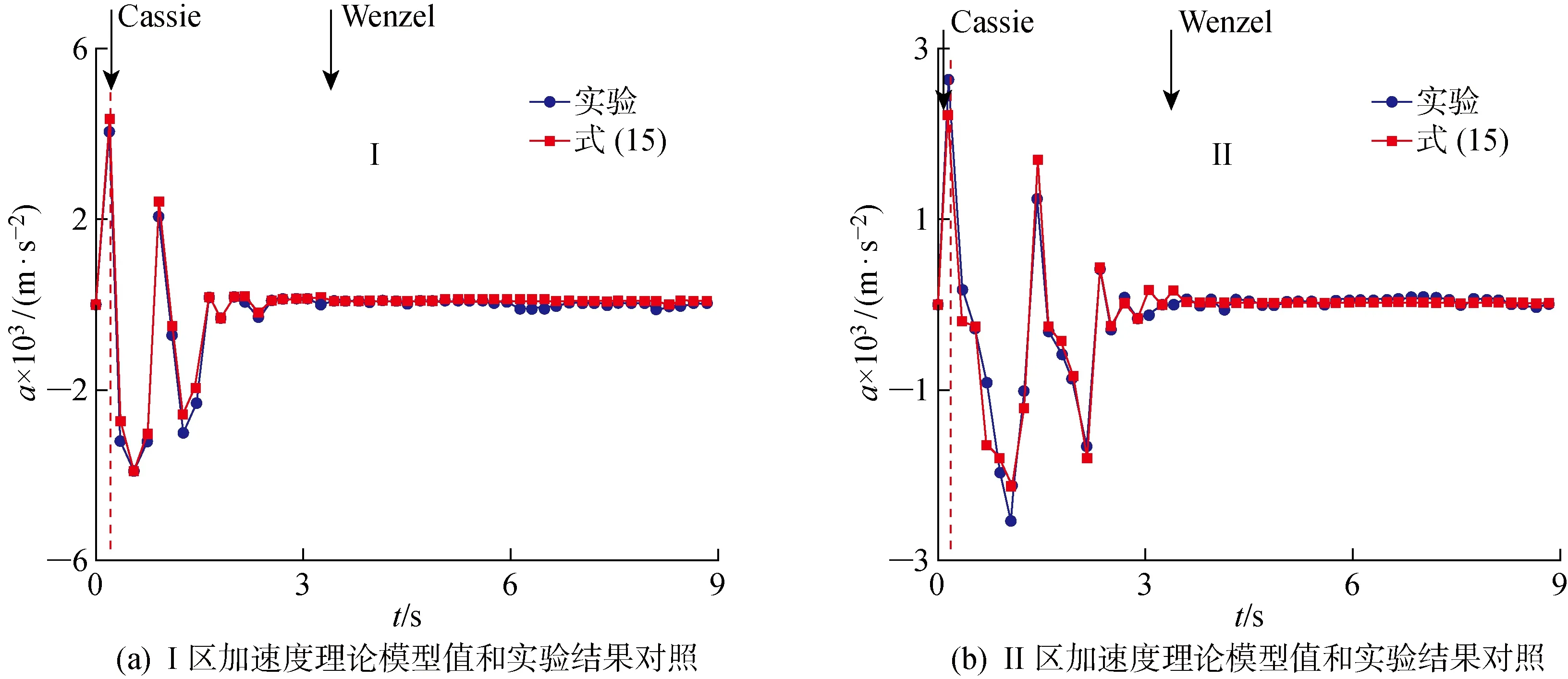
圖7 振動液滴運動時的加速度特征Fig.7 Acceleration characteristics of vibrated droplets in motion

3 結論

(1) 在微結構梯度能表面，隨著振幅的增加，液滴會發生由面積分數較大的區域向面積分數較小區域的定向運動.

(2) 在微結構梯度能表面，隨著振幅的增加，運動加速度逐漸減小，且在面積分數更大的表面的運動加速度更小，濕接觸直徑變化的范圍更大.

(3) 隨著液滴的定向運動，液滴會發生由Cassie狀態向Wenzel的浸潤狀態轉變，底部Laplace力消失，液滴的形變程度隨之逐漸減小，導致液滴受到的驅動力逐漸減小.此外，由于液滴濕接觸直徑的變化與浸潤狀態轉變的影響，液滴運動所受阻力不斷增加，液滴最終停止運動.

(4) 本研究為利用梯度能表面實現滴狀冷凝液滴的快速脫落提供了思路，尤其針對重力影響減弱狀態下，冷凝液滴不能利用重力自然脫落的情況.