有數學味的“折紙中的相似問題”再探討

趙正萍

【摘要】“折紙中的相似問題”這一課例，折射出了一節“數學味”濃的數學實驗課教學主要是通過操作、觀察、抽象、分析、歸納等思維活動獲得數學結論的.這一課例讓一張紙產生了教學價值，使學生體驗到了數學的學習從“聽”數學變成了“做”數學，從“被動接受”變成了“主動探究”.學生通過“做”數學實驗體驗發現的樂趣，感悟數學的真諦，發展數學思維，提高自身在實踐中解決問題的能力和創新意識，逐步積累數學活動經驗.

【關鍵詞】折紙;數學實驗;操作觀察;數學建模

案例背景：

對于數學實驗而言，許多學者給出了不盡相同的界定.曹一鳴認為，數學實驗是指實驗者為獲得某種數學理論、檢驗某個數學猜想、解決某類數學問題，運用一定的物質手段，在數學思維活動的參與下，在典型的實驗環境中或特定的實驗條件下所進行的一種數學探索活動[1].數學實驗課就是為“數學實驗”搭建的平臺，是“數學實驗”的數學環境，是激發學生數學思維的催化劑，是數學探索活動的一種新的模式，讓學生從有意義的接受學習，轉變為有意義的發現學習.

有效的數學學習活動不能單純依賴模仿和記憶，動手實踐、自主探索與合作交流才是學生學習數學的重要方式.《義務教育數學課程標準（2017年版）》提出：教師要結合教學內容，落實“雙基”走向“四基”，培養“兩能”發展為“四能”，促進學生數學學科素養的發展.數學活動經驗的積累是提高學生數學素養的重要標志.數學活動經驗需要在“做”的過程和“思”的過程中積淀，是在數學學習活動過程中逐步積累的.

教師在教學“折紙中的相似問題”這節課時，不能假借折紙操作，將本課上成一節只用相似解題的課，也不能上成只讓學生折紙的勞技課，而是要通過問題串讓學生學會運用折紙呈現出折疊類問題，同時構建相似問題的數學模型，要將這節課上成一節數學實驗與數學思維并存、有“數學味”的實驗課.

案例描述：

師：折紙可以產生全等圖形，那么會不會產生相似圖形呢？

活動一 任意三角形紙片的折紙

問題1.出示一張三角形紙片，請你通過折紙的方式，將∠A翻折，折痕為DE，A點的對應點為F點.

師：觀察翻折前后產生了哪些相等的量？

生：A點可能落在形內、形上、形外.DA=DF，EA=EF，∠ADE=∠FDE，∠AED=∠FED，∠A=∠DFE.（學生通過動手操作立即發現A點翻折后的位置有三種不同情況）

師：線段AF與線段DE有什么關系？

生：根據軸對稱的性質：對應點的連線被對稱軸垂直平分，即DE垂直平分AF.

師：能通過折疊，使圖形中產生相似的三角形嗎？

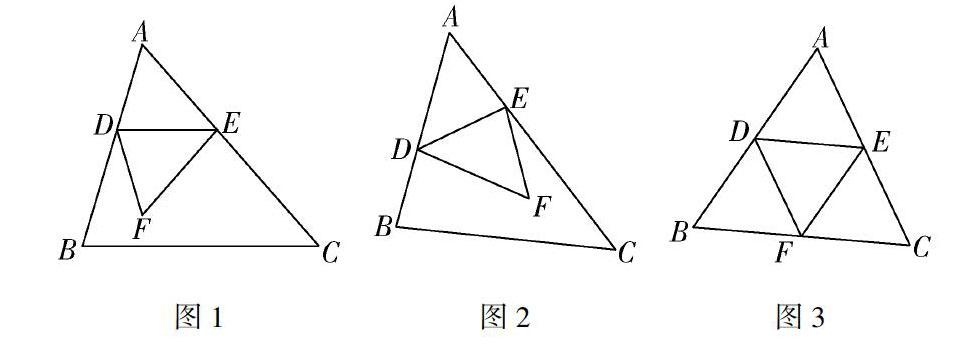
生：折成“平行相似”型（圖1）或折成“斜交相似”型（圖2）.（學生折出不同的折痕）

師追問 ：當折成平行相似中的A型相似時，怎樣折DE一定平行BC？

生：折成平行相似中的A型相似時，先折出高線AF，再對折，使點A與點F重合，這時折痕DE平行于BC.

在這一環節中，學生通過動手操作參與到學習中，通過觀察獲得感官刺激，感悟到折紙中蘊含的軸對稱變換知識.其次，學生折紙產生相似三角形，在頭腦中出現相似三角形基本圖形，通過動手操作找出相似模型，直觀形象.教師的追問再一次讓學生把折紙與數學知識聯系在了一起.

師：折疊時，如果A點落在邊BC 上（如圖3），那么△BDF和△CEF 一定相似嗎？

生：不一定.

師：怎樣改變圖形的形狀可以實現△BDF和△CEF 相似呢？

學生自然想到需要改變△ABC的形狀，引出活動二，過渡自然，調動學生的學習興趣.

活動二 特殊三角形紙片的折紙

問題2.將問題1中紙片的形狀改為等邊三角形，點A恰好落在BC邊上的點F處，△DFB與△CEF相似嗎？

師：折一折，觀察并找出圖中所有的相似三角形.

圖4生：折成圖4，F是BC上任意一點時，△BDF∽△CFE，△ADE∽△FDE（且全等）.

師：想一想，如果圖中四個三角形兩兩都相似，那么折痕DE需要滿足什么條件？（學生討論、交流發現：DE是等邊三角形ABC的中位線且A點的對應點F在BC的中點處）

師追問：如果△ABC為等腰直角三角形，△DFB與△EFC仍然相似嗎？需要滿足什么特殊條件？（學生有了前面的學習經驗，通過動手操作即可找出答案）

活動三 矩形紙片的折紙

師：剛剛研究了折疊三角形紙片產生的一些相似情形，如果翻折四邊形紙片能否產生相似三角形呢？哪種四邊形通過翻折產生相似三角形的可能性更大呢？

生：矩形.

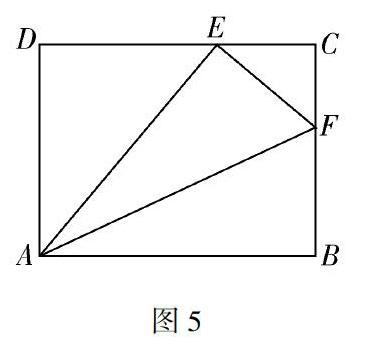
圖5問題3.如圖5，一張矩形（非正方形）的紙片ABCD，把∠B沿AF對折，使點B恰好落在CD邊上的點E處.

師：請同學們按照要求，翻折準備好的紙片，找出圖中的相似三角形.

生：△EAF∽△BAF（且全等），△DAE∽△CEF.（一張矩形紙片中∠B翻折后的位置也有三種情況，對點B落在邊上的特殊情況進行探究學習，操作后學生立即看出了“一線三等角”中的相似模型）

師追問1：圖5中這四個直角三角形一定兩兩相似嗎？

生：不一定.

師追問2：要使這四個直角三角形任意兩個都相似，四個直角三角形中的銳角應滿足什么條件？

生：四個直角三角形中的最小銳角是30度.

師追問3：滿足上述條件的四個三角形相似時，矩形長和寬的比是多少？（小組討論）

生1：通過設K法，設CF=x，運用勾股定理等知識求出了長∶寬=AE∶AD=2∶3.

生2：運用銳角三角函數求出ADAE=cos 30°=32.

師追問4：此時，E點在什么特殊位置？

生：E在CD的中點處.

師追問5：你能將手中的紙片通過折疊、度量或其他方法裁剪出符合上述要求的矩形嗎？（學生想出了兩種方法）

在這一環節中，學生通過折紙找出“一線三等角”中的相似三角形模型，用所學的知識找出了四個直角三角形出現兩兩相似時，紙片長與寬的比值要求.教師又追問：一張矩形紙片怎樣折可以滿足上述要求？其實怎樣折，就是在矩形紙片中構造出等邊三角形ABE.出乎意料的是學生有不止一種的折紙方案.一節課在折——探——折中，進行了折紙問題解決方案總結（圖6）.

案例反思：

1.折紙為學生提供了實驗探究學習的平臺

整節課從最基本的三角形入手，通過問題串的層層逼近，讓學生在折紙中感悟相似，讓學生經歷由簡單到復雜、由特殊到一般的探索過程.從一般三角形到特殊三角形（等邊三角形和等腰直角三角形），再從一般四邊形到特殊四邊形（矩形）的過程，讓學生深刻領會折疊的本質是軸對稱，而軸對稱的本質是圖形全等的不變性，涉及利用勾股定理列方程、相似中的一線三等角模型、特殊角的三角函數等核心知識和方法，對學生“動態變化、數形結合、邏輯推理、數學計算與數學建模”等數學素養的提高產生了積極影響.

2.實驗操作中的啟發

實驗操作是培養學生觀察想象和邏輯思維能力的重要途徑.學生通過觀察可以猜想數學結論，通過操作可以驗證邏輯推理得到的結論，還可以通過操作發現模型，運用所學知識解決問題或固化數學結論.學習折疊類問題的基本策略流程是：實驗操作——觀察猜想——推理論證——建模求解.因此，數學實驗課的設計一定要有立意，必須建立在思維活動上，如果離開了數學思維活動，數學實驗課就會變成一節按實驗程序操作的活動課，這樣就失去了數學味道，偏離了數學實驗課教學的軌道.

3.提升了學生的數學素養

“折紙出發——找相似三角形——回到怎么折”這一過程，通過數學問題的誘發，從操作開始，最后又回到操作上，讓學生邊折邊發現，將操作活動與想象、抽象、推理、計算聯系在一起，讓學生的大腦發揮尋找、驗證、構建等功能，激發學生的創新意識，讓學生在思考和提問中合作、討論、交流、實現數學思維與數學方法的自我完善，使學生在數學技能和數學思維得到發展的同時，自身數學素養也逐步提升.

4.給教師教學的啟示

折疊型操作問題就是運用軸對稱變換的性質解決問題，一直是中考的熱點.單獨提到軸對稱的性質，學生大多能夠理解和掌握.但具體到某些現實情境時，學生常常會感到困惑，其主要原因是學生不能把折疊問題快速轉化抽象出對應的數學模型，不會將數學問題進行直觀化的理解和設計.針對這種情況，在今后的教學中，教師要舍得花時間，讓學生通過動手實驗完成知識的學習，給學生充足的時間和空間，讓他們動手做、動手畫，讓學生體驗數學的樂趣.學生在“做”中學，在思中“悟”，體驗到數學學習在變“聽”數學為“做”數學，變“被動接受”為“主動探究”.學生通過“做”數學實驗體驗發現的樂趣，感悟數學的真諦，發展數學思維和智慧，提高實踐能力和創新意識，逐步積累數學活動經驗[2].

【參考文獻】

[1]曹一鳴.數學實驗教學模式探究[J].課程·教材·教法，2003（01）：46-48.

[2]喻平，董林偉.初中數學實驗的本質解析[J].課程·教材·教法，2016（08）：89-95.