不同計算形式的相關分析在氣象中的應用綜述
朱玉祥,江劍民,趙亮,劉海文,侯美亭,李宏毅,萬文龍,趙翠光
(1 中國氣象局氣象干部培訓學院,北京100081;2. 中國科學院大氣物理研究所LASG,北京100029;3. 中國民航大學,天津300300;4. 東營市氣象局,山東 東營257091;5. 國家氣象中心,北京100081)
1 引 言
在氣象科研和業務工作中,經常需要分析氣象變量變化的原因,這時可以把該氣象變量作為研究對象,分析該氣象變量與其它氣象變量之間的同期或前期關系。比如,在其它氣象變量中選擇一個變量,分析其對研究對象的影響,即分析一個變量與另一個變量之間的相關關系。如果二者相關關系顯著,則表明它們之間關系密切,可能存在因果關系或相互影響的物理過程,可以繼續深入分析其是否存在物理機理上的關聯;如果二者相關關系不顯著,則表明它們之間不存在密切關系。本文把氣象中變量相互關系或關聯性分析的方法稱為相關分析。相關分析在天氣[1-5]、氣候[6-10]、氣候變化[11-12]、農業氣象[13]、氣象服務[14]等領域廣泛應用。
變量之間的關系從統計學的角度大致可以分為兩類:函數關系和相關關系。函數關系要求非常嚴格,一般的數據很難滿足函數關系。而相關關系要求相對寬松,所以被人們廣泛接受,這也是相關分析在氣象變量關系研究中廣泛應用的原因。
雖然相關分析在氣象科研和業務中應用廣泛,但很多人對相關分析依然存在某些困惑,甚至存在誤用現象。因此,本文對氣象相關分析的現有成果進行梳理和總結,可以為關注氣象相關分析的科研和業務工作者提供借鑒和啟示。此外,氣象數據正在進入“大數據時代”[9,14],因此本文還簡要綜述了相關分析在“氣象大數據”中的應用價值和面臨的新挑戰。
2 氣象相關分析方法的分類
氣象科研與業務中經常使用的相關有:點(站點或變量)點相關、點場相關、場場相關。點點相關可以看作兩個變量之間的相關,點場相關可以看作一個變量與場中的每一個變量分別作點點相關,可以歸結為點點相關,因此也屬于兩個變量之間的相關。場場相關屬于多個變量之間的相關。因此,氣象中的相關大致可以分為兩類:兩個變量之間的相關和多個變量之間的相關。下面將分別介紹兩個變量之間的相關系數和多個變量之間的相關系數。
2.1 兩個變量之間的相關系數
2.1.1 兩個定距變量之間的相關系數
定距變量是指數值變量,不同的定距變量之間具有數量上的差別,可以對定距變量進行加減乘除運算。相關圖(或散點圖)和相關表可以反映兩個數值變量之間的相互關系及其相關變化的方向,但無法確切地表示它們之間相關的程度。度量定距變量相關性最常用的是皮爾遜相關系數[1-2,10,15-16]。
相關系數在科學研究中的應用具有悠久的歷史。1886 年,英國科學家高爾頓給出了關于遺傳的相關和回歸概念,并且思考了它們在生物遺傳研究中的可用性和價值[17]。著名統計學家卡爾·皮爾遜對高爾頓的“相關”概念十分著迷,經過深入研究,他在前人的研究基礎上,采用極大似然法,把一個二元正態分布的相關系數最佳值p用樣本積矩相關系數r表示,這被后人稱為“皮爾遜相關系數”或“皮爾遜積矩相關系數”(Pearson product-moment correlation coefficient,簡寫為PPMCC 或PCCs),文章中常用r或Pearson'sr表示。皮爾遜相關系數是最常用的普通相關系數,常簡稱為“相關系數”或“簡單相關系數”,兩個一維隨機變量x=(x1,x2,……,xn) 和y=(y1,y2,……,yn)之間相關系數的計算公式為:

皮爾遜相關系數r可以表示兩個隨機變量之間線性關系的強弱,其取值范圍為-1≤r≤1。r越趨近于1,這表示這兩個變量之間正線性相關關系越強;反之,r越趨近于-1,這時表示這兩個變量之間負線性相關關系越強;而當r等于0或接近于0時,表示這兩個變量之間不存在線性關系或線性關系很弱。r對于不同的相關現象,名稱有所差異,一般將反映兩變量間直線線性相關關系的統計量稱為相關系數(相關系數的平方稱為判決系數);將反映兩變量間曲線相關關系的統計量稱為非線性相關系數、非線性判決系數;將反映多個變量之間的多元線性相關關系的統計量稱為復相關系數、復判決系數。
皮爾遜相關系數是兩個變量之間關系的簡單單值度量,并且其形式適合數學運算,因此,應用非常廣泛。但需要指出的是,不能不加辨別地機械計算相關系數,因為皮爾遜相關系數無法識別非線性關系,并且皮爾遜相關系數對一個或幾個離群(異常)點極為敏感。如圖1 中的4 個子圖,皮爾遜相關系數全都相同,但顯然這4張圖的關系存在較大差異。此外,通常需要使用t檢驗對皮爾遜相關系數進行檢驗,而t檢驗是基于數據呈正態分布假設的,當變量數據不服從正態分布時,即使對大樣本,皮爾遜相關系數的顯著性檢驗也可能存在較大偏差。
對于點場相關,雖然常用皮爾遜相關系數進行研究,但也有很多研究者采用一元線性回歸研究點場相關。比如許立言等[18]研究歐亞大陸春季融雪與東亞夏季風之間的關系,就采用了一元線性回歸方法。他們選取春季融雪EOF 第2 模態的標準化時間序列,對850 hPa風場、500 hPa高度場和中國夏季降水場分別進行線性回歸分析。需要指出的是,如果用兩個原始變量(或距平變量)做一元線性回歸,這時由回歸系數得到的回歸場是帶單位的。而相關場是兩個標準化變量之間的相關系數得到的,是沒有單位的。回歸場與相關場的兩個場分布形勢略有差別,例如高度場的距平場,往往高緯地區距平變化大,標準差大,所以回歸場對高緯地區之間的關系反映得更大。而相關場則消除了高低緯之間標準差的不同,因此兩個場有相似的地方,也有不同的地方。對于變量x和y來說,回歸系數b與相關系數rxy之間的關系為其中sx和sy分別為x和y的標準差[15]。因此對于標準化之后的變量來說,回歸場與相關場之間并無差異。

圖1 子圖a,b,c,d的每個水平變量(x)都有相同的平均值9.0和標準差11.0,每個垂直變量(y)也都有相同的平均值7.5和標準差為4.12,對這4個子圖來說,皮爾遜(普通)相關系數是相同的,都為rxy=0.816[2]
皮爾遜相關系數在氣象科研中廣泛應用。比如,Wallace 等[19]對500 hPa 高度場和海平面氣壓場,計算了其中一個格點與場的其它格點之間的皮爾遜相關系數,發現在北半球冬季存在5個冬季遙相關型;丁一匯等[20]計算了點場之間的皮爾遜相關系數,研究了亞洲-太平洋季風區中的遙相關關系,清楚地揭示了東亞夏季風、印度夏季風和西北太平洋夏季風之間的相互作用。
2.1.2 兩個定序變量之間的相關系數
定序變量也稱為等級變量,其取值具有等級或次序之分。下面介紹3 種常用的定序變量相關系數。
(1)γ系數[21]。
γ系數的公式為:

式中,ns、nd分別為同序對、異序對的數目。同序對、異序對的定義為:某對樣本(x1,y1)和(x2,y2),如果在等級或次序上x1優于x2,并且y1優于y2,則稱為同序對;否則,稱為異序對。
這個公式的直觀意義是,相關系數定義為同序對和異序對數目的差與同序對和異序對數目的和之比值。比如:若ns= 0,則γ= -1,也就是說對于這兩個變量,所有的樣本對都呈現出異序,這時可以認為這兩個變量之間完全呈負相關關系;若nd= 0,則γ= 1,也就是對于這兩個變量來說,所有的樣本對都呈現出同序,這時可以認為這兩個變量之間完全呈正相關關系。
(2)Spearman相關系數[22]。
針對皮爾遜相關系數無法識別非線性關系,并且對一個或幾個離群(異常)點極為敏感的局限性,Spearman 相關系數可以作為皮爾遜相關系數的替代方法。
Spearman相關系數有時也被稱為級別(順序)相關系數或秩相關系數,該相關系數是根據兩個變量的秩(排序后的等級或順序值)進行相關分析,Spearman 相關系數可以用來衡量這兩個變量間是否存在單調相關關系。兩個一維隨機變量x=(x1,x2,……,xn)和y=(y1,y2,……,yn)的秩之間的Pearman相關系數定義為:

其中ri和si分別為xi和yi的秩,i= 1,2,……,n。當變量里出現相等值(秩結)的時候,該值對應的秩為這幾個值相對應的秩的平均值。Spearman相關系數可以簡化為式中Di為第i對數據之間秩的差值。
ρ的取值范圍為-1 ≤ρ≤1。當一個變量隨另一個變量單調遞減時,ρ= -1;反之,當一個變量隨另一個變量單調遞增時,ρ= 1。
只要兩個變量的值是成對的等級數據,或者是經由連續變量轉化得到的等級數據,就可以用上述Spearman 相關系數的公式進行計算,分析這兩個變量之間的關系。Spearman相關系數與變量的分布和樣本容量都沒有關系,并且具有魯棒性和抗干擾性,即計算結果對個別異常值不敏感。圖2 顯示了Spearman 相關系數與皮爾遜相關系數之間的關聯和差異。圖中兩個一維變量X和Y之間的皮爾遜相關系數為0.88,而它們之間的Spearman相關系數為1,表示它們之間的單調相關程度很強,等于1。

圖2 兩個變量X和Y的散點圖[23]
(3)Kendall相關系數[24]。
Kendall 相關系數是衡量等級變量相關程度的一個統計量,其主要思想是根據兩個變量間序對的一致性來判斷其相關性。
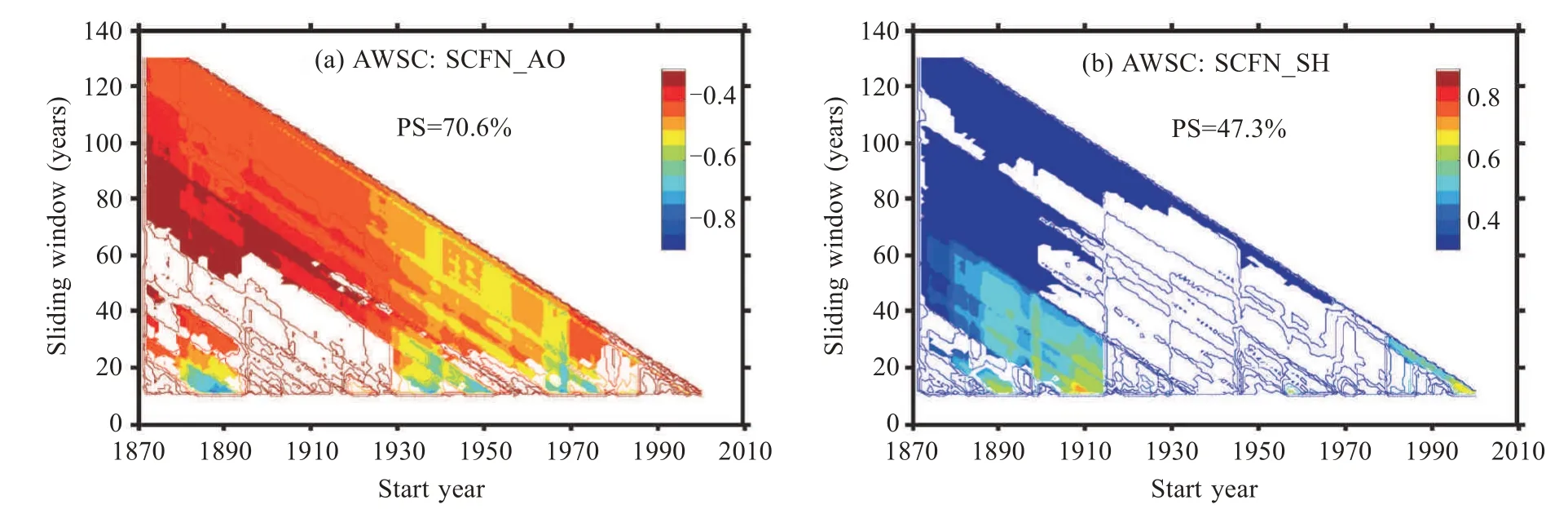
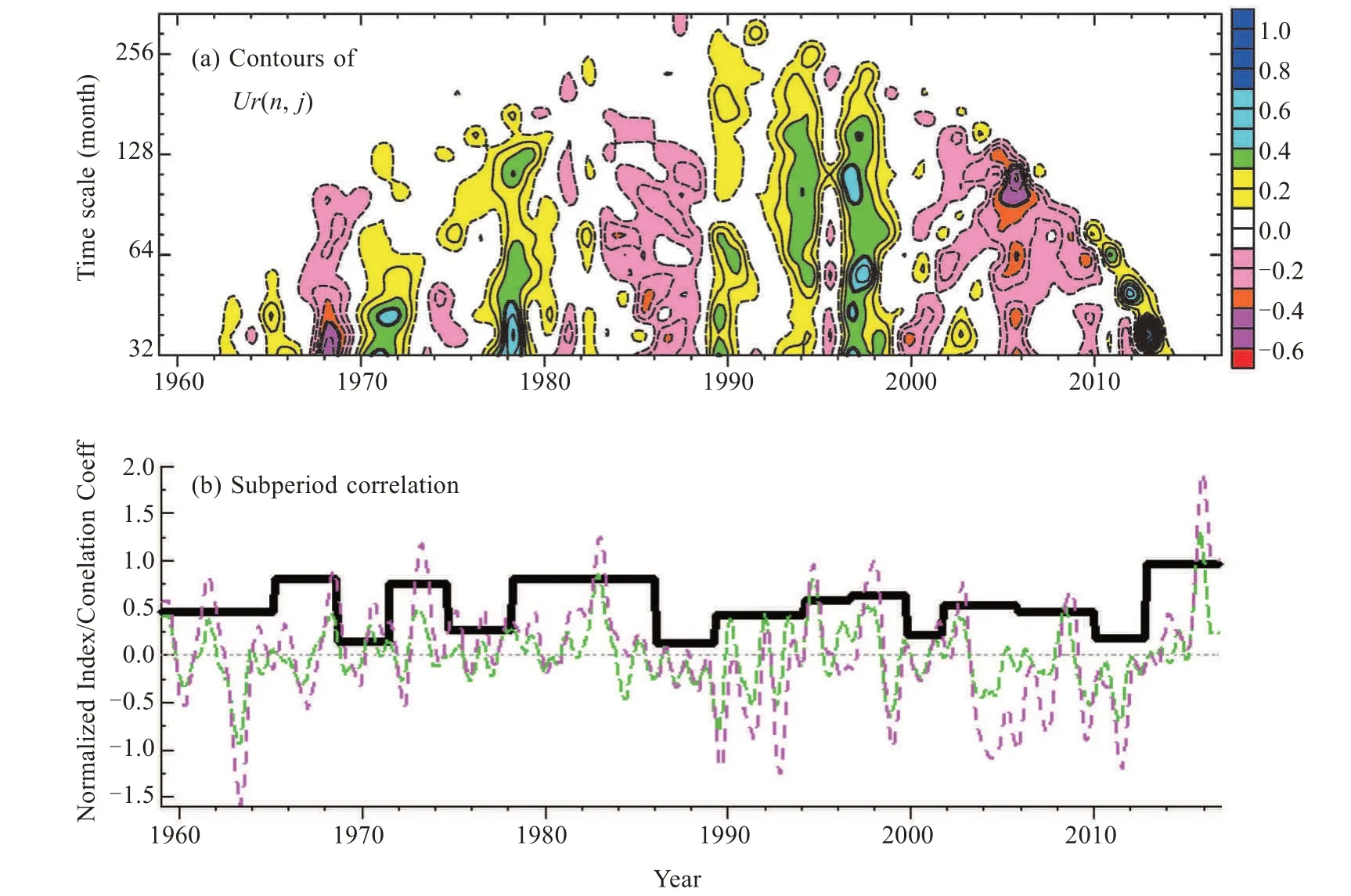
設x、y分別是兩個一維隨機變量,x=(x1,x2,……,xn)和y=(y1,y2,……,yn)。把(xi,yi)記為一個序對,序對之間的關系為下列三種情形:(1)當xi>xj且yi 那么,兩個一維隨機變量X和Y之間的Kendall相關系數τ定義為: 式中,S表示一致的序對個數。Kendall相關系數τ的取值范圍為-1≤τ≤1。當τ= -1 時,表示這兩個隨機變量具有完全相反的等級相關性;當τ= 1時,表示這兩個隨機變量具有完全一致的等級相關性;當τ= 0 時,表示這兩個隨機變量之間相互獨立。具體的氣象計算實例可參考文獻[1-2]。 2.1.3 兩個定類變量之間的相關系數 定類變量是指變量的值是研究對象的符號或名稱,每個值代表一個類別,這些值之間相互平等,沒有次序、大小的區別。 計算定類變量之間的相關關系可以借助列聯表。列聯表是數據按照兩個或更多個屬性進行分類后所列出的頻數表。假設有兩個屬性X和Y,屬性X有k類,用Xi表示第i類,i= 1,2,……,k;屬性Y有s類,用Yj表示第j類,j= 1,2,……,s。對于n個樣本,用nij代表既屬于特征X的第i類又屬于特征Y的第j類的樣本頻數。這樣可以得到一個k行s列的列聯表(表1)。 表1 列聯表的一般形式 下面,我們虛構一個簡單的2×2 列聯表,用來示例說明列聯表相關系數的計算。假設我們要研究性別(X)與天氣預報評分高低(Y)之間的關系,在調查的200 名預報員中,預報評分偏高的預報員中男性為70 名,女性為25 名,預報評分偏低的預報員中男性為30名,女性為75名(表2)。 表2 性別與預報評分高低相關分析的2×2列聯表 在定類變量相關系數的計算方法中,Q系數是最簡單的一種方法,Q系數只適用于2×2 列聯表,公式如下[25-26]: 為了理解Q系數的構造,我們取兩種極端情況。 若n12=n21= 0,則Q系數為1;若n11=n22= 0,則Q系數為-1。顯然,這兩種情況都表明性別與預報評分高低呈現出完全相關特征,而正負號表示相關關系方向的不同。在這個假設的例子中,Q系數為1 代表男預報員預報評分高,女預報員評分低;而Q系數為-1 代表女預報員預報評分高,男預報員評分低。 除了Q系數之外,還有λ系數、χ2檢驗、φ系數、C系數、V系數。由于篇幅關系,不再一一介紹,具體細節可參見文獻[25-27]。 2.2.1 偏相關系數 在二元或者多元回歸分析中,對于變量之間的相關關系,可用偏相關系數來表示。在研究多個自變量x1,x2,x3,……,xk與因變量y之間的線性相關程度時,如果其它自變量保持不變,只考慮y與其中某一個xi(i= 1,2,3,……,k)之間的關系,這種相關叫做偏相關。衡量偏相關程度的指標,就是偏相關系數。例如在二元線性回歸模型中,r01,2表示x2保持不變時y與x1的偏相關系數,r02,1表示x1保持不變時y與x2的偏相關系數,r12,0表示y保持不變時x1與x2的偏相關系數。在偏相關系數中,還可以根據固定自變量數目的多少,區分為零階偏相關系數、一階偏相關系數、K- 1 階偏相關系數等。例如,r0i(i= 1,2,3,……,k)表示零階偏相關系數(即簡單相關系數),r02,1(x1保持不變)稱為一階偏相關系數,r01,23(x2和x3保持不變)稱為2 階偏相關系數,r01,234(x2、x3和x4保持不變)稱為三階偏相關系數,依次類推。偏相關系數的具體計算公式和實例可以參考相關文獻[28-29]。 2.2.2 復相關系數 衡量一個變量(因變量y)與多個變量(自變量x1,x2,……,xp)之間線性關系的量稱為復相關系數。復相關系數的定義要涉及到多元線性回歸和剩余殘差的概念,具體計算公式和實例可以參考相關文獻[15]。 2.2.3 典型相關系數 典型相關系數是先對所研究的兩組變量進行主分量分析,得到新的線性無關的綜合指標,然后再計算兩組綜合指標之間的線性相關系數,進而研究這兩組變量之間的相關關系[1-2,10,15]。典型相關分析(CCA)可以有效地分離兩氣象場的最大線性相關模態。 奇異值分解(SVD)的出發點與典型相關相同,也可以用來分析兩個氣象場的相關模態,但計算要簡便得多[30-32]。從統計學角度講,CCA 推理更加嚴瑾,而SVD需要一定的使用條件[10]。 相關分析在氣象中的應用具有悠久的歷史。早在20 世紀初,Walker 在研究世界各地海平面氣壓變化之間的關系,提出全球“三大濤動”的概念時,就采用了相關分析的研究方法。后來,在大氣遙相關的研究中,也有不少文獻采用了相關分析方法[33-34]。下面介紹最近幾年相關分析中出現的一些新進展。 當計算兩個時間序列的相關系數時,由于相關關系往往并不穩定,所以當子序列的長度變化時,相關系數經常會發生變化,有時甚至會發生很大甚至完全相反的變化。那么如何量化評估時間序列之間相關的穩定性呢?Zhao等[35]提出的一種全窗口相關系數方法,可以有效地解決這個問題。 下面以他們文獻中的計算為例介紹該方法的計算過程。 根據概率統計知識,求相關系數的序列不能太短,因此規定滑動窗口最小為11(當然也可以根據所研究的具體問題相應調整)。 時間段為1872—2010 年,因此一共有139 年。所以滑動窗口為:11~129 年(確保滑動窗口有足夠的自由度和時間段)當滑動窗口為11(12,……,129)年時,所有可能時間段的總數為129(128,……,11),開始年從1872,1873,……,到2000(1999,……,1882)。因此,得到129(128,……,11)個相關系數。 最后,根據滑動窗口的大小,對每個相關系數做顯著性檢驗后,計算穩定度百分比(PS),PS 定義為顯著相關的數目相對于總相關數目N的百分比,這可以作為度量兩個序列之間相關穩定程度的指數。圖3中PS為梯形區域內彩色面積的百分比,對于圖3a 來說,PS=70.6%,意味著在不同的滑動窗口下大部分相關系數是顯著的,因此可以認為SCFN 和AO 之間的相關整體看是穩定的。而圖3b中PS=47.3%,意味著多于一半的滑動相關系數是不顯著的,因此SCFN 和SH 之間的相關整體看不是十分穩定。而且,通過全窗口滑動相關能夠辨識出信號穩定的時段和相應滑動窗口這二維信息,SCFN 和AO 之間的相關在1930年之后更穩定,從年際到80 a 尺度的相關都是穩定的;而SCFN與SH在1930年之后,相關變得不穩定。 圖3 1872—2010年期間冬季北半球雪蓋指數(SCFN)與北極濤動指數(IAO)(a)和冬季SCFN與西伯利亞高壓指數(ISH)之間(b)的全窗口相關系數 通過0.05顯著性檢驗的相關系數用填色等值線圖表示[35]。 小波分析可以對局部的時間或空間頻率進行分析,該方法通過平移伸縮運算對信號或函數進行多尺度細化,最終達到低頻處頻率細分,高頻處時間細分,該方法可聚焦到信號的任意細節,能自動適應時頻信號分析的精細化要求,因此小波分析被很多專家稱為“數學顯微鏡”。有學者用小波分析研究兩個時間序列的關系,Grinsted等[36]仿照Torrence 等[37]定義了兩個時間序列的小波相關為, 式中s是尺度,M 是平滑算子,具體計算公式可參考文獻[36]。小波相關的這個定義類似于傳統的相關系數,但分子中有平方,所以不同于傳統的相關系數有負值,小波相關系數全都為正值。小波相關系數通過位相表示傳統相關系數負值的意義。 一些研究應用這種方法檢測出了兩個因子間時間頻率的局部化信息和鏡像關系[27]。圖4是AO與BMI(波羅的海最大年海冰面積)小波相干譜。從圖4 中可以看出,1860—1900 年,2~6 年的時間尺度上存在大塊顯著相關區域,但中間的1865—1882 年,2~4 年的時間尺度上相關不顯著。在1960 年附近,2~3 年的時間尺度存在相關區域。在1900—1950 年期間,顯著相關的時間尺度從8~11 年變化為3~10 年。1915—1990 年期間,顯著相關的時間尺度從12~16 年變化為5~30 年。圖4 中所有這些顯著相關區域,平均位相角是174 °,顯示了AO 和BMI之間的反位相關系,并且AO 略領先于BMI。 氣象變量的相關關系存在突變現象,對相關關系的突變檢測具有重要的理論和實用價值。此前國內常用的M-K 秩和檢驗與Yamamoto 判據,一次計算都只能檢測序列中某一時間尺度的某次突變,而以前的小波分析,雖然可以進行多尺度分析,但沒有進行相關關系突變點的顯著性檢驗。 圖4 標準化的AO和BMI(波羅的海最大年海冰面積)時間序列之間的小波相關 相對于紅噪音的5%顯著性用粗等值線顯示。所有的顯著性區域顯示反位相行為。相對的位相關系用箭頭顯示(同位相指向右,反位相指向左,BMI超前AO 90 o指向正下,BMI滯后AO 90 o指向正上)[36]。 江劍民[38]提出了可以檢驗兩個序列間多尺度平均值突變現象的相干性(同步或反位相變化)的算法,并將該算法用于尼羅河年最高與最低水位歷史序列,可以較為客觀、自動地檢測出兩序列在不同時間尺度上突變的相干性。Jiang[39]融合小波分析的多尺度分辨功能和統計學4種參數,即平均值、方差、趨勢以及分段子樣本的相關系數,分別簡要概述了多尺度突變點的掃描式檢測算法。Zhu 等[40]進一步發展和完善了其中的相關系數和方差分析2 種算法,并且利用經過正態化處理后的珠江流域中的西江下游馬口水文站月平均流量與西江水域月降水量資料,給出了具體的應用實例,主要結果見圖5。 圖5 a. 馬口站月平均流量正態化指數NSI和西江流域月降水量正態化指數NPI之間相關系數的多尺度突變掃描式U檢驗結果的等值線;b. NSI(粉色虛線)和NPI(綠色虛線)13點高斯濾波低通曲線 兩序列樣本中分段子樣本相關系數突變點用黑色垂直粗線表示和分時段子樣本的相關系數用黑色水平粗線表示[40]。 圖5a 中橫坐標為月份時間(j,或稱為參考點),橫坐標表示尺度(n,即子樣本容量),等值線表示Zhu 等[40]中等式(4)定義的統計量Ur(n,j)。式(4)中Uα(n,j)是判斷相應尺度相關關系突變是否顯著的臨界值,α為顯著性水平,比如0.05、0.01 等。當樣本容量n>50 時,U0.05= 1.96,U0.01=2.58 ;當樣本容量n≤50 時,可采用學生氏t檢驗。但還需要對序列的非獨立性進行訂正[39]。理論上,Ur(n,j)< -1.0的局部最小值中心,表示相關系數顯著變小(弱);而Ur(n,j)>1.0的局部最大值中心,表示相關系數顯著變大(強)。由于本例總體數值較低,如放寬到0.4,可從圖5a 中找出14 個突變點。比如,1965 年4 月與時間尺度42 個月交匯處有一正極大值中心;1968 年9 月與時間尺度32個月交匯處有負極小值中心。接下來的極值點還有1971 年7 月與42 個月尺度上的正極大值,1974年9 月與42 個月尺度上的負極小值,1978 年4 月與37 個月尺度上的正極大值,1986 年2 月37 個月尺度上的負極小值。1989 年和1998 年之間的三個局部正極大值表示相關關系的接連增強。1999—2010 年之間的3 個負極小值表示相關關系的接連下降,但期間包含有一個2001年10月于37個月時間尺度上的小正值中心。整個圖面上表現出最強的突變點發生在2012 年12 月37 個月的時間尺度上,超過了0.1 的顯著性檢驗。由圖5b 可見,兩條經過平滑濾波后的曲線可以直觀地驗證粗黑實線所標示的突變點及其相對應的子樣本時段的相關系數變化情況。這種算法,在數學界也獲得較好的認可與評價。 最近幾年,學術界就大數據在體積、類型、速度和價值這四個方面的特征基本達成了共識,即大數據的4V 特征:Volume(大體積),數據量為ZB級別;Variety(多樣性),除傳統的結構化數據之外,還有大量的非結構化數據;Velocity(高速度),秒級的數據分析處理以及輸出;Value(價值稀薄),有效信息占信息總量的比例小。氣象數據與氣象服務對象的數據也基本具備了大數據的上述特征[41-44],特別是隨著氣象及氣象服務對象數據的進一步豐富,未來必將進入氣象大數據時代[9,14],而基于大數據的人工智能技術也已經在天氣預報和氣象服務中得到應用[45]。 現有的知識體系是建立在數據稀缺背景下的,在大數據時代,人們的思維和工作方式必須發生變革。相關分析已經成為大數據挖掘與分析的關鍵應用技術和核心科學問題[46],在大數據分析中相關關系比因果關系更重要[47],這指明了相關分析在大數據應用和分析中的重要地位。在大數據研究和機器學習中,相關分析常被稱為關聯分析,就是在關系數據、市場交易數據,或其它可用的信息載體中,查找可能存在的關聯、相關性或因果結構。關聯分析是一種簡單實用的分析技術,可以發現存在于大數據集中的相關性,從而可以描述事物中某些屬性可能出現的規律和模式。關聯分析常用的方法有FP-G 算法、Apriori 算法、FreeSpan 算法、Prefixspan 算法等。在大數據相關分析的應用領域中,引人關注的是推薦系統,即基于相關分析度量出物品相似性、用戶相似性等特征,進而對不同的顧客進行精準的產品推薦[48],從而可以避免傳統廣告中“普遍撒網”,推薦目標不準確的缺陷。對于氣象服務網站來說,基于相關分析的產品推薦也有應用前景。在災害應急管理中大數據相關分析也有著廣泛應用[49]。 Wang 等[9]指出,根據大數據的思想和分析方法,聚類分析、相似分析、相關分析和機器學習技術在大數據時代的氣候預測中將被廣泛應用。其實,在氣象大數據時代,這些技術在天氣預報和氣象服務中也廣泛使用。需要指出的是,聚類分析、相似分析和機器學習,都離不開相關分析,因此相關分析是氣象大數據分析中十分重要的技術方法。 對于氣象大數據來說,降低數據的維度或者簡化數據是一項重要工作,經驗正交函數(EOF)分解或主分量分析(PCA)是一種重要的降維方法[50-51],EOF 及其變種方法在氣象的多個領域都具有重要應用。EOF 分解得到的是空間分型模態,它的某一分量的空間荷載值就是該分量的時間系數與該格點的時間序列樣本之間的相關系數。其實也可以看作為相關場,與用EOF 空間模態絕對值最大的點為定點的點場相關得到的皮爾遜相關系數相關場類似[52],EOF 通常也稱為分型模態。 對大數據來說,數據關系往往呈現非線性、高維度等復雜特征,傳統的相關分析方法往往難以有效地探測數據的內在結構與規律,迫切需要新的相關分析計算方法。下面介紹大數據研究領域出現的兩種具有代表性的新算法。 (1)距離相關。Szekely等[53]從特征函數的距離視角考察了兩個隨機向量之間的非線性相關系數,為高維數據的非線性分析提供了有效的度量準則。距離相關具有如下兩個優點:①所度量的相關也包含非線性關系,而不僅僅局限于線性相關關系;②可以度量任意兩個不同維數的隨機向量的相關性。但距離相關系數要進行高維向量間的距離計算和矩陣乘積運算,所以計算耗時很大,對計算能力要求較高。氣候變化研究[54]中使用了該方法。 (2)MIC 相關性。2011 年,《Science》上發表了一篇題為“Detecting novel associations in large data sets”的論文[55],該論文提出了衡量兩個變量之間相關關系的一種新方法——最大信息系數(Maximal Information Coefficient, MIC)。MIC 具有兩個重要性質:通用性和均等性。通用性是指,傳統的相關系數往往只能度量某種特定類型的函數類型(如線性、指數、對數或周期性函數)變量之間的相關程度,而MIC 可以度量任意函數形式變量之間的相關性,因此具有通用性。均等性是指,對于具有相等MIC值,但函數形式不同的數據,外加同等程度的噪音,然后重新計算MIC,這時MIC的值仍能保持相等,而傳統的相關系數計算方法很難做到這一點。該方法比皮爾遜相關系數、Spearman相關系數等方法更細致地描述和刻畫了兩個變量之間的相關關系,但該方法目前在氣象領域的應用還較少。 由于大數據具有數據規模大、數據類型復雜、價值密度低等特點,這為相關分析帶來了很多挑戰和困難,表現最突出的就是計算效率問題。楊靜等[56]針對傳統大數據典型相關分析(CCA)方法的高復雜度在面臨大數據PB 級數據規模時不再適用的現狀,提出了一種基于云模型的大數據CCA方法,該方法在云計算架構的基礎上,通過云運算將各端點云合并為中心云,并據此產生中心云滴,以中心云滴作為大數據的不確定性復原小樣本,在其上施以CCA 運算,進而提出了具有較高計算效率的大數據CCA 分析的云模型。Nguyen 等(2014)[57]提出了一種高維相關子空間的搜索方法,該方法基于相關圖的極大團進行挖掘分析,克服了傳統Apriori 算法采用的逐層搜索模式計算耗時高的弊端,為大數據中進行多變量高維相關分析提供了一種快速便捷的計算方法。并行計算也是加快計算能力的有效手段,以MapReduce 為代表的非關系數據型庫管理技術為大數據分析與處理提供了一種并行處理架構[46],可以為大數據相關分析的并行計算提供理論支持。云計算和并行計算領域對相關分析的這些研究,對于開展氣象大數據相關分析研究具有重要的借鑒意義。 氣象領域在應用相關分析的時候,有幾個問題是需要注意的。 (1)需選擇有物理意義的氣象變量做相關分析。在氣象研究中做相關分析時,不能濫用。只有具有物理意義的變量之間做出的相關,才能更加穩定,在預報預測中也更有價值。 (2)當計算相關的兩個變量都包含明顯的趨勢變化成分時,原變量之間的相關特征可能被歪曲(夸大或者縮小)。施能等[58]的數值試驗結果表明:兩個變量帶有相同性質的趨勢時,這兩個變量之間的相關系數會增加,具體表現為正相關系數值被夸大,負相關系數值被減小;而當這兩個變量帶有性質相反的趨勢變化時,則會使這兩個變量之間的相關系數減小,具體表現為正相關的數值被減小,而負相關的數值被夸大。 (3)需要做嚴格的顯著性檢驗。根據概率統計的術語,我們得到的氣象資料應稱為樣本。無論氣象資料的時間有多長,都是有限的,而氣象變量的總體是無限的。當根據有限的樣本推斷無限總體的性質時,必須進行顯著性檢驗。具體檢驗方法可參考相關文獻[59-60]。相關系數的檢驗不應該稱為“信度檢驗”,其檢驗水平也不應該稱為“95%置信度”,而應該稱為“顯著性檢驗”,顯著性水平為5%(10%,1%)[60]。如果把點場相關中相關系數高于或低于某一數值繪圖為陰影區,那么這些區域應該稱為“超過或高于顯著性水平5%(10%,1%)的區域”,相關系數的檢驗過程應該稱為“顯著性檢驗”。顯著性水平α需要取小值,氣象中常取5%(10%,1%)。現在的很多統計軟件(比如SAS、SPSS、Matlab、R 等)中,計算相關系數時,常自動給出P值,當P值小于5%(10%,1%)時,即可以說這兩個序列的相關超過顯著性水平5%(10%,1%)。 當多個統計檢驗結果必須被同時評估的時候出現了特殊問題,這被稱為“檢驗的多重性問題”[2]。比如求點場相關時,在相關場中逐點進行相關系數檢驗完成后,如果在若干個格點上表現是顯著的,那么是否可以認為這個相關場是顯著的呢?這個問題已經由Taleb[61]根據所謂的“無窮猴子理論”進行了有趣的說明。如果我們能以某種方式,把無窮數量的猴子放在鍵盤前,并且允許它們隨機的打字,事實上,肯定有一只猴子最終能打出Iliad。但是據此推斷,這只猴子與眾不同是不合理的。例如,推斷這個猴子接下來比其它的猴子有更高的概率打出Odyssey。假定無限數量的猴子打字,一只猴子復制出可辨識內容的事實,并沒有提供反對原假設的充分證據,即這只是一只普通的猴子,其將來的文字輸出,與其它任何猴子沒有什么不同。Livezey 等[62]用概率論的觀點把含N個格點的相關場的檢驗看成N次擲硬幣試驗,即每個格點只有兩種檢驗結果:通過和不通過檢驗的兩個互斥事件,實際上這是一個二項分布檢驗問題。設檢驗的顯著水平為0.05,那么對某一格點來說,成功通過檢驗的概率為p= 5%,不成功的概率為q= 95%。根據二項分布,即可以計算出N次試驗中,M次事件成功發生(該問題中則為總格點數N個中有M個格點通過檢驗)的概率。例如,當場的總格點數為N=30時,4個點通過檢驗的概率為0.045,5 個點通過檢驗的概率為0.016,……。這樣,可以計算“至少4個點通過檢驗”事件的概率為0.045 + 0.016 +……≈0.062。從而可以確定出相當于0.05 水平下的臨界點數。該例的計算表明,在顯著性水平0.05 下,該相關場至少需要超過4.24 個點通過檢驗時才能認為該相關場是顯著的,即其顯著區域面積為總場格點數的14.1%(4.24/30)時,該場是顯著的。類似可以計算,當總格點數為N=80 時,顯著臨界區域面積為10%,N=500時,顯著臨界區域面積為7%。 兩個氣象變量的相關系數是否顯著,可以采用t檢驗,但當氣象變量本身具有強的持續性或高的自相關時,t檢驗的自由度不能用n- 2,而應該用有效自由度,有效自由度的計算方法[63-64]可以參考文獻[27]。當然,這時也可以采用蒙特卡洛檢驗[17,48]。當對時間序列做了滑動平均后再求相關時,這時的有效自由度就發生了變化,就可以采用蒙特卡洛檢驗,具體的例子可參考宋燕等[65]的例子。 天氣預報和氣候預測正在進入大數據和智能預報時代,這對相關分析提出了新要求。大數據的核心是預測,大數據之所以能夠預測未來,是基于對相關關系的準確把握。傳統的統計方法對樣本數據的正態性、變量的獨立性、變量個數、假設檢驗等都有較高要求。大數據技術是對傳統數量統計學方法的拓展和延伸,大數據分析側重于高維建模、復雜網絡建模、非參數模型等技術方法從種類繁多、數量龐大的數據中快速獲取有價值的信息[57,66-67]。大數據時代氣象科研和業務工作對相關分析提出了新要求,根據我們的理解,可能主要表現在以下方面。 (1)對于不符合正態分布的變量如何做相關,并且檢驗其相關的顯著性。 (2)如何對變量之間不同尺度的信號求相關,以及把這種多尺度的相關應用在天氣預報和氣候預測中。 (3)如何求非線性相關?可能是一個值得深入研究的問題。因為傳統的皮爾遜相關系數所求得的相關關系只是線性關系。而很多氣象變量之間存在復雜的非線性關系,如何客觀定量地描述這種非線性關系,需要進一步深入研究。 (4)如何解決相關分析的高效計算問題?未來氣象大數據也將具有數據規模大、數據類型復雜、價值密度低等特點,如何在平衡計算能力和業務時效之間提高計算效率,是需要深入研究的問題。可能需要在并行計算和云計算方面對相關分析算法做深入研究和改進。 本文系統綜述了不同計算形式的相關分析在氣象中的應用,特別是最近幾年相關分析的新進展,盡管仍然會掛一漏萬。希望本文能夠為關注氣象數據分析理論與應用的專家提供借鑒相關分析作為探尋與發現氣象變量內在規律的重要工具,在氣象大數據分析與挖掘中具有重要應用,但在大數據時代面臨新的挑戰,尚存在不少問題值得深入研究。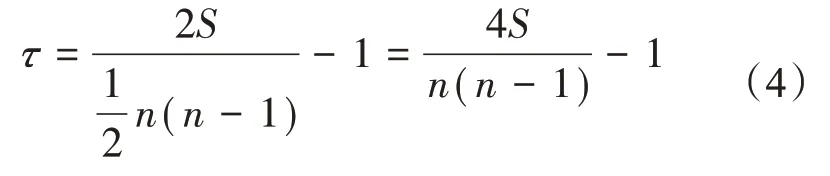


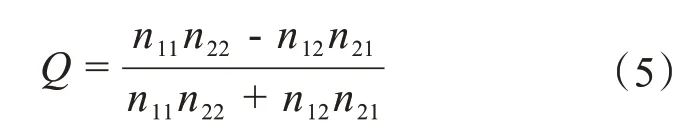
2.2 多個變量之間的相關系數
3 相關分析在氣象中應用的新進展
3.1 全窗口滑動相關

3.2 小波相關

3.3 兩序列相關(相干)的多尺度突變檢測

4 氣象大數據中的相關分析
4.1 氣象大數據的特點
4.2 相關分析在大數據中的作用
4.3 氣象中的降維方法與相關分析的關系
4.4 大數據相關分析的新方法
4.5 大數據相關分析面臨的挑戰和困難
5 氣象相關分析應用中存在的問題
6 相關分析在氣象中應用的未來發展趨勢

