活用教材，厘清數學核心概念

張義瑛

在概念教學中，教師要以典型、豐富的實例為載體，引導學生展開觀察、分析，抽象概括出概念的本質屬性，歸納得出數學概念。概念教學不能只是走過場，要給予學生充分概括數學概念的機會。數列概念的內涵很小，而其概念的外延很大，學生對數列概念掌握的難點在概念的外延上。

【教學重點、難點】

重點：數列及其有關概念，感受數列是刻畫自然規律的數學模型及其廣泛應用;理解數列通項公式的意義。

難點：會根據前幾項寫出它的一個通項公式，理解數列與函數的關系。

【教學目標】

1.理解數列通項公式的意義，對于比較簡單的數列，會根據數列的前幾項，寫出它的一個通項公式，培養觀察、歸納能力。

2.通過實例體會序號與項之間的對應關系，理解數列是一種特殊函數，培養聯想、類比學習能力，為下節課研究數列的函數特性做好鋪墊。

3.培養數學抽象、邏輯推理能力。

【教學過程】

一、創設情境，理解概念

師：今天我們將進入新一章的學習，首先讓我們從一段密碼開始，這是電影《達·芬奇密碼》中館長索尼埃留下的密碼提示（圖略），這顯然不是他最終要傳遞的信息。接下來，我們通過影片來看探長是如何破譯密碼的。

（教師播放《達·芬奇密碼》電影探長破譯密碼片段）

師：電影《達·芬奇密碼》中有這樣一段情節：盧浮宮館長索尼埃被殺時留下了一段密碼和信息，你能從短片中看出探長破譯后的明文和原來的密碼之間有什么關聯嗎？

生：數字相同，順序不同。

師：探長發現索尼埃留下的密碼其實就是打亂了順序的斐波拉契數列，從而得到啟示，將英文字母重新進行組合找到了謎底。這個破譯密碼的過程又告訴我們什么呢？

生：它告訴我們，相同的數字按照不同順序排列也會有不同的意義。

師：很好！這正是我們本節課要研究的主題：數列。

【設計意圖】教師通過電影情節引入新課，激發學生的學習興趣，讓學生理解數列概念，辨析數列概念，同時結合課本封面出現的斐波拉契數列，引出本節課要研究的主題：數列。但更深層次的用意是讓學生認識到，即使數字相同，但排列順序不同，也會產生不同信息，這是我們研究數列的本質原因。

（教師出示數列的定義：按照一定次序排列著的一列數叫作數列）

師：請大家繼續對比這兩組數，斐波拉契數列是世界上著名的數列，你能觀察出它的規律嗎？

生：從第三項起，后一項是前兩項的和。

師：那么索尼埃的密碼有類似規律嗎？索尼埃的密碼是數列嗎？

生：沒有類似規律，索尼埃的密碼是數列。

師：為什么索尼埃的密碼是數列？

生：因為索尼埃的密碼也是有順序的。

師：這兩個數列是同一個數列嗎？

生：不是。

師：說明什么？

生：數列具有有序性。

【設計意圖】概念教學的核心是：在學生最近發展區激發學生的認知沖突，讓學生的思維和教材內容彼此碰撞，學生對所學內容產生強烈的興趣和求知欲望。在教學中教師充分發揮引導作用，讓學生進一步理解數列概念，將數列概念幾個易混點解釋清楚。

二、感受數列，構建概念

教師從不同領域給出教學情境，讓學生充分感受數列的廣泛存在。

1.拉面在對折過程中的根數：2，4，8，16，32，64，128，256，…

2.婚禮上的酒塔由頂層到底層的酒杯數：1，3，5，7，9。

3.“一尺之棰，日取其半，萬世不竭。”1 ， 1/2 ，1/4 ，1/8 ，?1/16 ， …

4.1988年到2016年中國奧運金牌數：5，16，16，28，32，51，38，26。

師：你還能舉出我們日常生活中的數列嗎？

......

師：請問數列1的通項是什么？

生：是[2n]。

師：你是如何得到的呢？

生：因為第一項可以寫成[21]，第二項可以寫成[22]，第三項可以寫成[23]，所以第[n]項就是[2n]。

師：請問這里的指數[1，2，3，…，n]是數列的什么？

生：是數列的序號或者項數。

師：所以我們找數列的通項實質上是找什么？

生：數列的序號與數列項之間的對應關系。

師：如果數列[an]的第[n]項[an]與序號[n]之間的關系可以用一個式子表示成[an=fn]，那么這個式子就叫作這個數列的通項公式。

【設計意圖】本教學環節中，教師從不同的領域讓學生感受到數列在生活中大量存在，體會數列是刻畫事物發生、發展規律的數學模型（有序性），教師運用幾個實例引入數列相關概念，幾個數列都有背景：數列1是等比數列，數列2是等差數列，兩者都是遞增數列。數列3是等比數列也是遞減數列，數列4用來說明不是所有的數列都有通項公式。學生通過實例抽象概括數列相關概念，培養了數學抽象、邏輯推理能力。學生切身體會數列的項與序號之間的對應關系，寫出一些簡單數列的通項公式，為突破本節課的難點做準備。

三、辨析概念，學以致用

教師出示1988年到2016年中國奧運金牌數：5，16，16，28，32，51，38，26。

師：你能根據這些金牌數，得出下屆奧運會中國獲得的金牌數嗎？為什么？

生：不能，因為該數列沒有規律，所以不能寫出該數列的通項公式。

師：有了通項公式，只要依次用[1，2，3，…]代替公式中的[n]，就可以求出這個數列的各項，也就是說每個序號都對應著一個數（項），我們把例1換種形式寫出來。

師：大家通過該數列序號與項的這種對應關系聯想到什么？

生：映射。

師：很好，再觀察序號與項這種數與數的對應關系，我們會進一步聯想到什么？

生：函數。

師：從函數的觀點看，發現了什么？

生：數列項是序號的函數。

師：數列也是函數，請問這個函數的定義域是什么？

生：正整數集[N+]。

師：數列可以看成以正整數集[N+]為定義域的函數，當自變量從小到大的順序依次取值時，所對應的一列函數值就是這個數列。

師：這個函數的解析式是什么？

生：數列的通項公式就是該函數的解析式。

師：數列也是函數，那和我們學過的一些基本函數有什么區別嗎？

生：數列的定義域為正整數集[N+]。

師：所以數列的圖像是什么？

生：是一群孤立的點。

……

【設計意圖】本教學環節中，教師運用實例說明通項公式的作用：已知通項公式可以求出數列中的任意項。教師通過求數列中的項，讓學生領會序號與項之間的對應關系，由對應關系聯想到所學的函數。學生通過類比分析，找到數列與函數之間的關系：數列是特殊的函數。教學中，教師注重知識的生成過程，培養學生分析問題、解決問題的能力。

【教學反思】

一、活用教材，創設合適的教學情境是幫助學生理解概念的關鍵

教學的關鍵在于教師依據教材，理解教材的意圖，把握數學概念本質，進而創造性地使用教材。在教學中，教師關注知識的整體構架，挖掘日常生活素材，在數學抽象的過程中落實數學素養。

首先，挖掘生活中的數列（拉面在制作過程中的根數）、文化中的數列（一尺之棰，日取其半，萬世不竭）、體育中的數列（中國奧運健兒從1988年奧運會到2016年奧運會所獲得的金牌數），這些數列均能刻畫客觀事物的發生發展過程（有序性），把現實生活中的一些數量與圖形有關的東西引入數學教學，這就是第一次“感性抽象”，抽象出數列的有序性。

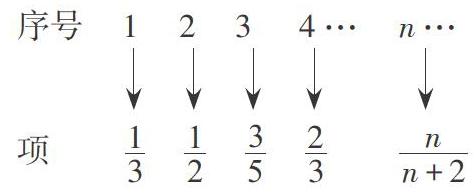
其次，圍繞主題“如何用函數刻畫數列的有序性”，做如下處理：根據[an=nn+2]的通項公式，分別寫出數列的前5項。在寫出數列前5項的過程中，學生概括出數列是自然數集到實數集的映射，進而抽象出數列可以看成以正整數集或它的有限子集{1，2，…，n}為定義域的函數，當自變量按從小到大的順序依次取值時，所對應的一列函數值就是這個數列（從數學的角度刻畫了數列的有序性），這就是第二次“符號抽象”，用抽象的數學符號刻畫數列，其特征是符號表達，這樣有利于學生深刻理解數列概念。

二、設計課例“明暗結合”，遵循概念學習的規律

我們根據兩條線索設計這節課。一條是數列及其相關概念、數列與函數的關系這一知識技能的“明線”，一條是從典型事例中抽象出新的數學概念的“暗線”。

數列概念的獲得應該符合學生的認知規律，讓學生在教學情境中認識到研究數列及其相關概念的必要性，在探究過程中，歸納概括出數列的特征、性質，培養學生的數學核心素養。教師遵循概念教學的規律，設計了“感知概念—形成概念—辨析概念—應用概念”的教學過程。課例從引入斐波那契數列開始，到鼓勵學生課外探究斐波那契數列的通項公式結束，整個教學過程浸潤數學文化，滲透數學思想，達到了提升學生數學核心素養的目的。

（作者單位：江西省九江市第一中學）