基于掌控板和數據分析 探究熱敏電阻阻值與溫度關系
李琦 施艷紅

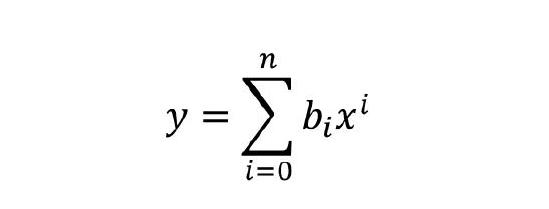
摘要:熱敏電阻的阻值會隨溫度的變化而變化,它是接觸式溫度傳感器的核心元件。能否準確得到阻值與溫度的關系直接影響到溫度傳感器測量值是否準確。但是阻值與溫度的關系并非簡單的線性關系,本文討論了基于實驗數據采集與多項式回歸的方法建立熱敏電阻阻值與溫度關系數學模型,并得到對應解析表達式的過程。
關鍵詞:熱敏電阻;掌控板;數據
中圖分類號:G434? 文獻標識碼:A? 論文編號:1674-2117(2021)08-0077-04
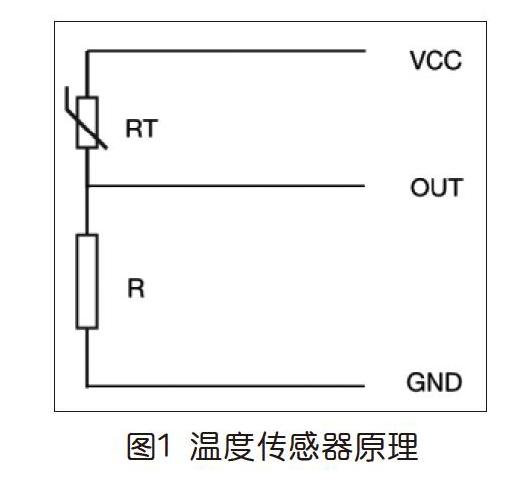
熱敏電阻一般由電阻溫度系數(TCR)較大的材料制成,根據其電阻與溫度變化關系,可以分為正溫度系數(PTC)熱敏電阻和負溫度系數(NTC)熱敏電阻。接觸式溫度傳感器一般以熱敏電阻作為核心元件,通過如圖1所示的電路得到隨溫度變化的電壓信號。
其中,VCC接電源正極,GND接電源負極,RT為熱敏電阻,R為對溫度變化不敏感的定值電阻。RT與R形成分壓電路,根據歐姆定律,此時OUT端與GND之間的電壓U與電源電壓Vcc、熱敏電阻阻值Rt、定值電阻阻值Rs之間存在如下關系:
將上式整理后可得到:
Vcc、Rs可以看作是定值,因此通過測量U的值可以計算得到熱敏電阻當前阻值Rt。若該熱敏電阻的溫度-阻值變化規律已知,則可以進一步計算得到對應的溫度。為了得到某熱敏電阻其溫度-阻值變化關系,可以通過實驗采集數據,并通過分析數據來開展探究。
● 設計實驗,采集數據
一般地,開源硬件中的模擬輸入口是一個模-數轉換器,并且默認會以Vcc作為基準電壓,如掌控板的P0口就支持12位模-數轉換,且基準電壓為3.3V。若P0口讀取到的模擬值為2047,則表示當前P0口的電壓為≈1.65V。
準備掌控板、1KΩ定值電阻、燒杯、玻璃溫度計、待測熱敏電阻以及若干導線,其中待測熱敏電阻的金屬引腳需要用絕緣材料進行包裹,以避免金屬引腳與水接觸造成測量不準確。根據圖2所示電路將各部分進行連接,為了導線連接方便,本案例實驗裝置使用了掌控擴展板。實驗裝置實物如下頁圖3所示。
為了讓掌控板記錄數據,在掌控板中上傳如圖4所示的代碼。
實驗時,先打開掌控板,將熱敏電阻和玻璃溫度計放置到燒杯內,在燒杯內倒入開水直至浸沒熱敏電阻和溫度計,等待玻璃溫度計讀數上升到80℃以上后按下掌控板A鍵。時刻觀察玻璃溫度計讀數,每次玻璃溫度計到達掌控板上顯示的目標溫度,就按下B鍵。
實驗結束后,在mpython軟件中連接掌控板,并在控制臺中輸入rec,便可以得到記錄的數據,如圖5所示。
● 數據整理與分析
有許多軟件支持數據整理與分析。相比之下,使用Python編程進行數據整理與分析可以更加靈活、深入,利用Python的pandas模塊、numpy模塊和matplotlib模塊可以方便、高效地開展數據處理與分析。Jupyter Notebook是一個交互式筆記本程序,它支持Python程序的分段編寫與運行,并實時顯示輸出結果,因此非常適合應用在數據分析領域。
1.實驗數據讀取與整理
將mpython軟件切換到Jupyter模式,并新建一個Jupyter項目。運行如圖6所示的代碼可以將實驗數據保存到data對象中。其中rec字符串的值可以從圖5所示的mpython控制臺中復制得到。
data是一個DataFrame對象,溫度值記錄在data對象的temp列中,對應的模擬值記錄在vot列中。根據模擬值計算阻值,并將結果保存到resis列中。此外,為了方便查看數據,還需要根據溫度值對數據進行升序排序。具體代碼如圖7所示。
2.繪制散點圖,觀察數據規律
為了直觀地看到數據的分布規律,以data中的溫度值作為橫坐標數據,對應的電阻值作為縱坐標數據,利用matplotlib模塊繪制散點圖。參考代碼與運行結果如圖8所示。
從散點圖中可以看出,該熱敏電阻阻值隨溫度增加而增加,屬于正溫度系數熱敏電阻(PTC),且阻值與溫度存在非線性關系。
● 建立多項式回歸數學模型
為了得到熱敏電阻阻值與溫度的數學關系,需要通過回歸分析的方法得出電阻關于溫度變化的函數表達式。回歸分析的方法有很多,其中研究一個因變量與一個或多個自變量之間多項式的回歸分析方法,稱為多項式回歸(Polynomial Regression),當自變量只有一個時,稱為一元多項式回歸。一元多次多項式的回歸方程為:
其中y為因變量,x為自變量,b_i為回歸系數。多項式回歸方程可以通過增加自變量x的高次項來逼近,因此在某個確定的定義域范圍內,任意連續可導函數都可以用多項式來擬合。
在本案例熱敏電阻的阻值與溫度的關系中,熱敏電阻的阻值可以看作自變量,溫度則作為因變量。因此,可通過一元多項式來進行回歸。一元多項式回歸的核心,就是找到合適的回歸系數b0...bi,使得阻值樣本數據R下通過一元多項式計算得到的溫度預測值Tp與樣本數據中真實溫度值Tr的均方誤差(MSE)最小。從圖像上看,就是讓回歸方程的圖像盡可能地逼近所有的樣本數據點。
利用numpy模塊的polyfit方法可以快速地進行一元多項式回歸。在圖9所示的代碼中,利用溫度值作為x值、電阻值作為y值進行了最高次為2次多項式回歸。
多項式回歸的系數保存在coef列表中,具體的系數采用了科學記數法。根據coef參數值,回歸方程為:
可以通過如圖10所示的代碼定義predict函數,以方便回歸方程的計算。
為了直觀地了解回歸結果,可以利用predict函數預測20~100℃時熱敏電阻的阻值,并將圖像與觀測數據一起繪制到同一張圖表中,代碼與運行結果如圖11所示。
● 模型評估與修正
得到數學模型后還需要對模型進行評估與修正。從圖11中可以看出,該多項式回歸模型與觀測數據的擬合程度并不是很好,特別是低溫段。除了觀察圖表,還可以通過均方誤差來評價模型。如圖12所示的代碼定義了rmse函數并計算預測值與觀測數據的均方誤差。
嘗試在圖9所示的代碼中修改polyfit函數的參數,逐個增加多項式的高次項,當最高次為3次時,模型圖像與均方誤差如圖13所示,無論是圖像表現還是均方誤差都有改觀。
逐步增加高次項可以進一步提高模型的擬合程度,本案例中最高次與均方誤差的關系如下表所示。
但是,多項式最高次數并非越大越好,隨著次數的增加,多項式回歸模型容易出現“過擬合”現象,所謂的過擬合是指回歸模型與觀測數據的擬合程度很好,但預測數據的表現很差。如圖14所示的是多項式最高次數為8時的函數圖像,可以明顯看出模型在高溫段失效。
因此,本案例中的熱敏電阻阻值R與溫度T的關系可以通過一個7次多項式方程來表示:
R=(4.89005432e-11)+(1.21358405e-07)*T-(3.49422507e-05)*T2+(3.98052301e-03)*T3-(2.31129452e-01)*T4+(7.36089221e+00)*T5-(1.22738958e+02)*T6+(1.53919756e+03)*T7
事實上,多項式回歸模型也有其局限性,它在觀測數據范圍內表現較好,而在觀測數據范圍之外則容易失效。例如,上述方程在定義域[0,100]的函數圖像如圖15所示。可以看到利用該回歸模型并不能準確預測低于20℃時的熱敏電阻阻值。
與傳統教學方式相比,項目式教學更有助于培養學生的動手能力、創新能力和探究精神,可以讓學生更深入地掌握、理解、應用學科知識。但項目活動的開展往往涉及多學科的知識,利用開源硬件采集實驗數據并結合數學建模與Python編程,可以開展許多學科實驗探究活動。本案例涉及信息技術、數學、物理等學科內容,體現了信息技術學科計算思維、數字化學習與創新,數學學科數學建模,物理學科實驗探究等學科核心素養。希望通過本案例能給大家帶來更多的啟發。
參考文獻:
[1]史麗萍,孫寶元,于浩洋.多項式回歸分析在傳感器測試中的應用[J].河北工業大學學報,2003,32(03):41-44.
[2]伊德里斯.Python數據分析基礎教程:NumPy學習指南:第2版[M].北京:人民郵電出版社,2014,1.

