拖拉機—牽引式農機具的運動建模與跟蹤控制*

張培培，楊自棟，趙相君

(浙江農林大學工程學院，杭州市，311300)

0 引言

拖拉機可以與附裝的、懸掛的或牽引的農機具一起完成起壟、播種、噴藥、收獲等大部分田間作業。科技部在“數字農業”建設戰略研討會上提出，以“精準農業”和“智能農業”為切入點，組織實施數字化農業科技行動，實施精準農業，廣泛應用智能農業機械，提高資源利用率和經濟效益[1]。因此拖拉機自動駕駛技術已成為農業裝備智能化研究熱點之一[2-6]，其研究方向主要分為車輛行駛軌跡規劃和車輛軌跡跟蹤控制兩個方面。

隨著控制技術的發展，國內外眾多學者對拖拉機路徑跟蹤進行了建模并提出了相應的控制策略。應用較多的有PID控制[7]、模糊控制[8]、滑模控制[9]、模型預測控制(Model Predictive Control，MPC)[10]、非線性模型預測控制(Nonlinear Model Predictive Control，NMPC)[11]等。

拖拉機是與農機具或掛車完成田間作業，因此近十年來眾多學者開始對拖拉機牽引農機具或者掛車系統進行自動駕駛的路徑跟蹤控制進行研究[11-15]。Backman等[11]建立了基于拖拉機—牽引式農機具運動學模型的NMPC路徑跟蹤系統，設計的NMPC控制器能夠保證拖拉機和農機具在牽引速度12 km/h時的橫向誤差最大誤差為10 cm。Kayacan等[12]建立了拖拉機掛車機組的縱向和橫向的非線性動力學模型，設計的PID控制器使掛車機組有效地跟蹤曲線路徑。Cariou等[13]研究了農用車輛—牽引式農機具在地頭轉向和速度自動駕駛控制，并設計了基于運動學模型前進和倒退的路徑跟蹤控制器，系統以0.5 m/s速度倒車沿期望路徑行駛80 m時，農機具的后軸中心的橫向誤差在±20 cm。Karkee等[14]研究了拖拉機單軸牽引農機具系統，分別建立了運動學模型、動力學模型和高度仿真模型，試驗證明當牽引速度小于4.5 m/s和輸入頻率小于1 rad/s運動學模型能較好地反映車輛行駛時的運動學特性，并設計了基于拖拉機牽引農機具運動學模型的閉環LQR控制器跟蹤期望路徑。

本文針對拖拉機—牽引式農機具系統在運動軌跡假設的基礎上建立運動學模型。該系統是本身存在一定運動約束的一類欠驅動系統，既獨立控制輸入少于自由度的系統，且具有非線性，因此為簡化穩定跟蹤控制器的驗算和求解，本文應用準確線性化方法對建立的模型線性化，最后采用滑模變結構算法來實現對拖拉機—農機具系統的跟蹤控制，并通過仿真手段分析和驗證了控制算法的有效性和實時性。

1 運動學模型建立

為簡化研究問題，作如下假設：車輛只作平行于地面的平面運動；車輛速度較低，車輪沒有側滑；拖拉機和牽引式農機具鉸接點在拖拉機的后軸中心。這樣，拖拉機—牽引式農機具系統就可以簡化為如圖1所示模型。

1.1 直線軌跡

拖拉機—牽引式農機具的直線行駛運動軌跡跟蹤模型如圖1所示，(XOY)為卡迪爾坐標系，使農機具跟蹤X軸，X軸為期望路徑，即控制目標為y2→0，θ→0，γ→0。

圖1 拖拉機—農機具直線跟蹤運動模型Fig. 1 Line path tracking model of tractor-trailer system

根據圖1模型建立拖拉機—農機具系統的直線運動學微分方程

(1)

(2)

(3)

(4)

(5)

以P點橫坐標x2為新的時間量標，新量標x2與時間t之間的關系

(6)

式中：V1——拖拉機后軸中心速度。

式(1)～式(5)可以改寫為

(7)

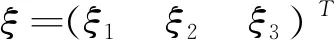
(8)

(9)

則拖拉機—農機具的線性化狀態方程

(10)

因此可以為該線性系統設計一個負反饋線性控制器u作為新系統輸入

(11)

根據式(11)，拖拉機前輪轉角α如式(12)。

(12)

式(10)、式(11)表明，設計合理的負反饋控制器u會使系統快速穩定，當x2不斷增大時，ξ→0，根據式(8)得到y2→0，θ→0，γ→0即車輛直線運動時會跟蹤X軸。式(12)表明，前輪轉角α由u、θ，γ決定。

1.2 圓弧軌跡

圖2為拖拉機—農機具系統圓弧軌跡示意圖，農機具車軸中心的期望路徑的半徑為R，農機具車軸中心的實際位置用極坐標(r，φ)表示，用以跟蹤期望路徑，極坐標的圓心為期望路徑的圓心O，O1為拖拉機的瞬時回轉中心，O2為農機具的瞬時回轉中心。

圖2 拖拉機—農機具圓弧跟蹤運動模型Fig. 2 Circle path tracking model of tractor-trailer system

以期望路徑的弧長l=Rφ作為新的時間量標，以(r-R)→0，θ→定值，(γ-φ)→90°為控制目標。根據圖2模型建立新量標l與時間t的關系和拖拉機—農機具的圓弧運動學微分方程

(13)

(14)

將式(14)通過坐標變換進行準確的線性化，得到與式(10)類似的系統線性化模型。

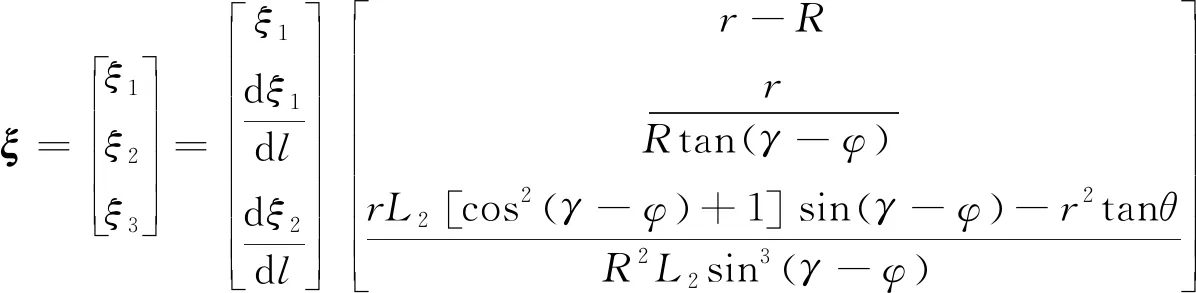
(15)

(16)

根據式(16)可以求出拖拉機前輪轉角α如式(17)。

(17)

設計合理的負反饋控制器u會使系統快速穩定，當新的時間量標l不斷增加，ξ→0，r快速收斂到R。式(17)表明，極坐標系下拖拉機—農機具系統圓弧軌跡跟蹤時拖拉機前輪轉角α由u、r、θ和γ-φ決定。

2 基于滑模變結構控制算法設計

拖拉機—牽引式農機具系統具有明顯的非線性，前面將該系統進行準確的線性化為反饋線性控制提供了基礎。本文采用滑模變結構算法來實現對該線性化模型的跟蹤控制。

2.1 滑模面的參數設計

設有線性系統

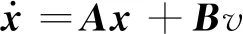
(18)

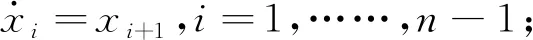
A、B——系數矩陣；

v——輸出矩陣控制函數。

滑模面設計為

(19)

n——狀態變量的維數。

根據本文建立的拖拉機—農機具的模型是一個三階系統，即n=3。

2.2 基于指數趨近律和準滑動模態的滑模控制器設計

滑模控制包含趨近運動和滑模運動兩個過程。為了保證快速趨近同時削弱抖振，本文采用指數趨近律的方法和準滑動模態控制。

指數趨近律

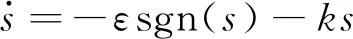
(20)

式中：ε——等速趨近速率，ε>0；

k——指數趨近項系數，k>0。

ε和k決定了趨近切換面時的速度。

(21)

式中：δ——很小的正常數。

(22)

根據Lyapunov穩定性理論，系統是穩定的，結合式(18)～式(21)得到系統的變結構滑模控制律

(23)

合理地選擇切換函數矩陣C可以保證滑模變結構控制系統具有良好的動態特性，C的選取方法主要有極點配置法、二次型最優等，Ackermann公式可以簡單有效地進行極點配置[18]，故本文基于Ackermann公式進行極點配置選取C。線性系統(18)是一個閉環三階系統，具有3個都位于左半開復平面的極點，其中2個共軛主導極點λ1、λ2由系統的參數決定，為使第3個實數極點λ3對系統的影響小，應使其遠離兩個主極點。

根據文獻[12]確定系統的固有頻率和阻尼為ωn= 2.26 Hz，ζ=0.70，則主導極點

(24)

第3個極點λ3遠離2個主導極點，取λ3=-10。

根據Ackermann公式

(25)

其中：f(A)=(A-Iλ1)(A-Iλ2)(A-Iλ3)。

根據式(25)可以求出c1=40.3，c2=32.0，c3=12.8，取ε=0.5，k=3，δ=0.01，則系統的滑模控制律為

(26)

3 路徑跟蹤仿真試驗分析

一輛自制的青山牌輪轂電動拖拉機和小型半掛車組作為仿真試驗用車，拖拉機的軸距L1=1.4 m，鉸接點到半掛車軸的距離L2=1.2 m。

根據上述滑模變結構控制器的設計，搭建仿真模塊并在Matlab/Simulink環境下分別進行拖拉機—農機具系統的直線和圓弧路徑跟蹤仿真，假設運動速度穩定在1 m/s。設置初始時刻為t0=0，末端時刻t1=30 s，求解算法采用龍格—庫塔數值解法，設定模型仿真步長為0.01 s。

3.1 直線軌跡跟蹤

系統的直線軌跡跟蹤初始條件如下：y2=0.5 m，θ=0，γ=π/6，仿真試驗結果如圖3所示。

(a) 狀態變量隨時間變化歷程

(b) 前輪轉角隨時間變化歷程

(c) 農機具與拖拉機夾角隨時間變化歷程

(d) 農機具與X軸夾角隨時間變化歷程圖3 直線跟蹤仿真結果Fig. 3 Straight-path-tracking simulation results

線性化系統的狀態變量ξ經過約3 s 后均收斂到0，農機具的后軸中心P點的Y坐標y2=ξ1從初始位置0.5 m增大到約0.67 m后迅速收斂于期望路徑X軸；前輪轉角α經過約5 s收斂到0°；農機具與拖拉機夾角θ在(-60.26°，22.24°)波動后快速收斂到0°；農機具與X軸夾角γ在(-26.38°，30.00°)波動后約5 s后收斂到0°，說明農機具可以跟隨拖拉機沿著期望路徑行駛，因此設計的控制器可對直線軌跡進行跟蹤。

3.2 圓弧軌跡跟蹤

拖拉機—農機具系統的圓弧軌跡跟蹤初始條件如下：r-R=1 m，θ=π/18，γ=π/2，φ=π/10。參考軌跡圓的半徑依次設計為5 m、10 m和20 m，仿真試驗結果如圖4所示。

(a) 狀態變量隨時間變化歷程

(b) 前輪轉角隨時間變化歷程

(c) 農機具與拖拉機的夾角隨時間變化歷程

(d) (γ-φ)隨時間變化歷程圖4 圓弧軌跡跟蹤仿真結果Fig. 4 Curved-path-following simulation results

從圖4(a)中看出，線性化系統的狀態變量ξ經過約3 s收斂到0，農機具的車軸中心P點的實際半徑與期望半徑差(r-R)=ξ1從初始值1 m快速收斂到0。圖4(b)、圖4(c)和圖4(d)可以看出，R依次為5 m、10 m 和20 m 時，前輪轉角α經過約7 s分別快速收斂到期望值16.14°、8.97°和5.09°；農機具與拖拉機的夾角θ分別收斂到13.47°、6.81°和3.40°；(γ-φ)均快速收斂于90°，說明農機具的縱向中心軸線與期望軌跡圓弧快速相切，這些表明農機具的回轉中心O2收斂于期望路徑的圓心O，由此可見設計的控制器可對曲線軌跡進行跟蹤。

4 結論

1) 應用非線性相關理論對欠驅動拖拉機—牽引式農機具系統動態規律進行了分析，以此建立了拖拉機—牽引式農機具系統的直線和圓弧行駛運動軌跡跟蹤模型，為達到簡化運動的目的，應用準確線性化方法對建立的非線性系統模型線性化。

2) 采用滑模變結構算法設計了拖拉機—牽引式農機具系統的跟蹤控制算法。最后利用Matlab/Simulink對系統仿真試驗，結果表明：設計的控制器可以使線性化系統的狀態變量ξ經過約3 s收斂到0，在直線跟蹤時，農機具從初始位置y2=0.5 m經過約3 s跟蹤到期望路徑X軸，農機具與拖拉機夾角及農機具角度偏移量均在5 s左右收斂到0°；在跟蹤半徑為5 m、10 m 和20 m的圓弧軌跡時，農機具車軸中心從偏離期望圓弧半徑1 m的初始位置經過約3 s可以跟蹤到期望圓弧，農機具與拖拉機夾角均可快速收斂到定值，同時農機具的回轉中心O2收斂于期望路徑的圓心O，因此農機具的后軸中心P點能迅速跟蹤不同期望路徑，驗證了控制算法具有良好的道路跟蹤精度和動態性。