梯度策略的多目標GANs帕累托最優解算法

張 波，徐黎明，2，黃志偉，要小鵬

1.西南醫科大學 醫學信息與工程學院，四川 瀘州646000

2.重慶郵電大學 計算機科學與技術學院，重慶400065

近年來，生成對抗網絡（Generative Adversarial Nets，GANs）[1]在深度學習和圖像處理領域取得了巨大的進展，與之前的深度生成模型[2-3]相比，GANs 具有強大的數據擬合和近似能力。它不僅消除了馬爾可夫和可展開近似推理網絡的約束，也為擬合各種數據提供了靈活的框架。GANs的概念和框架相對較新，但已成為一個熱門的研究主題。正如LeCun 所說，GANs 是過去十年中機器學習領域最令人興奮的想法。到目前為止，GANs 在Google 學術中的引用量已超過17 000 次。隨著GANs理論的不斷成熟以及與其他技術的融合，它被廣泛地應用于包括圖像復原[4-6]、圖像超分辨率[7-9]、圖像隱寫術[10]、文本-圖像合成[11]、圖像-圖像轉換[12-13]、圖像分類[14]和圖像檢索[15]等多個圖像子領域。

在以生成對抗網絡或者對抗訓練為基礎的圖像模型中，其目標函數往往包含多個損失項，每項損失代表一個目標，旨在完成一種特定的任務，并且這些損失項之間往往存在相互“矛盾”甚至“競爭”的關系。求解這類非凸函數的全局最優解較難，大部分GANs模型不會直接尋求全局最優解，而是先利用交叉驗證的方法確定最優權重參數，然后再利用梯度策略和線性搜索方法，沿著梯度下降的方向，搜索帕累托最優解。但這種方法存在2個明顯的缺陷：

（1）當目標數量較多時，采用交叉驗證方式確定權重參數的過程非常耗時，并且得到的權重參數不能保證對于整體參數求解是最優的。

（2）當目標數量較多或者參數梯度的維度較高時，線性搜索并不能直接應用到大規模學習任務。

根據文獻[16]的總結，大部分面向應用的GANs 模型都包含多個損失函數，并且含有大量參數，梯度的維度較高，這給求解參數最優解帶來了巨大挑戰。對此，本文提出基于梯度策略的多目標生成對抗網絡的帕累托最優解搜索算法。

1 相關工作

與多目標優化相關的是多任務學習，有文獻[17]證明可以通過多目標優化來解決多任務學習，并簡單認定在優化層面多任務學習等同于多目標優化。當給定多個任務或多個目標時，尋找帕累托最優解是一個多目標優化問題。在機器學習中，多目標優化可以歸納為，訓練一個模型來執行多個任務，而多個任務之間可能存在相互“矛盾”的關系，多目標優化則能夠優化一組可能沖突的目標或任務。常見的優化方法是選擇優化代理目標，即，通過最小化多個損失的加權線性組合來進行優化。多目標優化或多任務學習可以通過建立歸納偏差，然后最小化單個任務經驗風險的加權和來進行參數求解。

早期的多任務學習認定，對比獨立地學習每個任務，使用來自多個任務的數據能夠取得更好的性能[18]。多任務學習通常是通過參數共享進行的，在實際求解過程中，參數共享分為硬參數共享和軟參數共享兩種方式。硬參數共享方法中，一部分參數共享，另一部分參數依賴于特定的任務。采用軟參數共享方法時，所有參數都基于特定任務，并且所有參數都被貝葉斯先驗或聯合詞典約束。現階段，基于梯度策略的多目標優化方法都是基于硬參數共享實現的，因此，本文重點關注這類方法。

Baxter等人[19]從理論上將多任務學習問題分解為個體學習者與元算法。每一個學習者要負責一項任務，元算法決定怎樣更新共享參數，上述提到的優化代理目標就使用加權求和作為元算法。基于這種方式，后續有學者提出了許多改進方式。Li 等人[20]提出每個學習者都基于核學習來進行多目標優化。Zhou 等人[21]首先假設所有的任務共享一個詞典，然后提出使用期望似然最大化的元算法來實現多目標優化。此外，Zhou等人[22]還提出了群體多目標優化策略。隨著多目標優化問題研究日漸成熟，還有學者將多主體學習[23]，順序決策[24]和貝葉斯優化[25]應用到多目標優化問題中。

此外，基于梯度策略的方法也被提出，并取得較好的結果。Fliege[26]和Désidéri 等人[27]利用Karush-Kuhn-Tucker（KKT）條件，找到所有目標經驗風險的梯度下降方向，然后在此方向上進行線性搜索。由于硬件設備的不斷發展，這種策略隨后又被擴展到利用隨機梯度更新，Poirion等人[28]與Chen等人[29]提出了基于不確定性隨機梯度策略的方法用于多目標卷積神經網絡的優化。

與本文所提算法最接近的是MGDA[27]算法和Frank-Wolfe[28]算法，二者都基于梯度策略進行線性搜索，但這兩種算法適合目標數較少以及參數梯度維度較低的情況，并不能有效地處理目標數較多的情況。由于GANs包含多個深度神經網絡，擁有巨量的參數，梯度維度較高。因此，MGDA 算法和Frank-Wolfe 算法不能直接適用于多目標GANs優化。基于這兩種算法，本文所提算法將多目標優化問題分解為多個兩目標優化問題，然后再沿著梯度下降的方向進行梯度更新和線性搜索。

2 本文工作

原始的生成對抗網絡[1]優化采用梯度上升法優化判別器，同時采用梯度下降法優化生成器，后續許多GANs 改進模型都基于這類梯度策略。由于原始的GANs 中只有一項損失，即，用于擬合真實數據流形的對抗損失，這種梯度策略非常有效。但在面向任務的GANs 模型[16]中往往包含多種損失。如，圖像復原任務中，包含重建損失、視覺感知損失等；圖像-圖像轉換任務中，包含循環一致性損失，邊緣保持損失等。不難證明，包含多個損失的目標函數是非凸的，可以將這個非凸函數總結為：

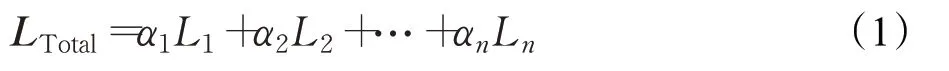
其中，L={L1,L2,…,Ln}表示不同的損失或者目標，α={α1,α2,…,αn}表示不同的權重參數。現階段，基于梯度策略的多目標GANs 都采用硬參數共享方法來求解。因此，可以將GANs模型的參數θ 分為共享參數θs和特定參數θk。結合式（1），可以得出優化式為：

其中，K 表示目標數量。前文提到，可以將多任務學習看作是多目標優化問題，即，優化一組可能沖突或競爭的任務。因此，式（2）可以展開為：

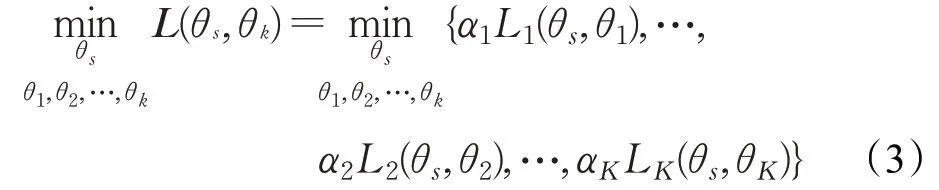
求解式（1）和（3）這類包含巨量參數的非凸函數的全局最優解較難，是一個可證明的NP難問題。因此，大多數算法選擇尋求帕累托最優解。

對于不同的目標數量，本文采取不同的求解方法。根據GANs 綜述論文[16]，大體上將目標數分為K=1、K=2 和K ＞2 三種情況進行求解。在基本的圖像合成任務中[1]，任務數K=1，不存在相互沖突的任務或目標。此時可以認定帕累托最優解即為模型的全局最優解，按照GANs提供的梯度策略方法進行求解即可。當任務數K ＞1 時，GANs 的結構多為深度編碼-解碼結構。對此，將編碼器參數設置為共享參數，解碼器參數設置為特定參數進行求解。

2.1 兩目標帕累托最優解（K=2）

現在已經有一些基于梯度策略的方法能夠有效搜索帕累托最優解。MGDA 就是一種典型的方法，該方法通過添加KKT（Karush-Kuhn-Tucker，KKT）條件到共享參數和特定參數上，進行求解。

文獻[27]已經證明滿足上述KKT 條件的任何解均為帕累托最優解，并且，帕累托最優解要么為0 且所得模型參數和權重參數滿足KKT 條件，要么帕累托最優解位于參數梯度下降方向。因此，所得的多目標優化算法是針對任務特定參數的梯度下降，即，求解：

此時，搜索帕累托最優解比較容易，可以計算式（5）（二次方程）的最優權重參數為：

當確定最優權重參數后，可視化搜索帕累托最優解的過程，如圖1所示。

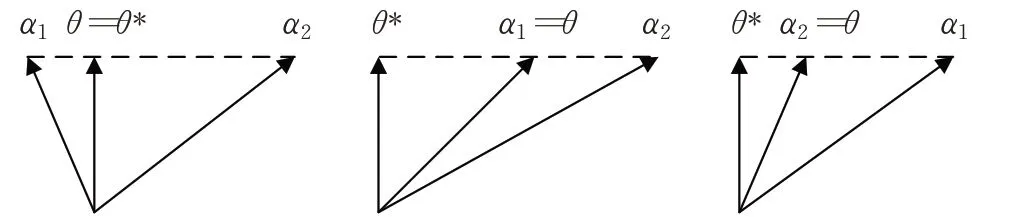
圖1 K=2時，三種可能的帕累托最優解

根據以上分析，可以得出當K=2 時的搜索算法，如算法1所示。

算法1兩目標帕累托最優解算法

圖1 表明，當K=2 時，帕累托最優解的范圍較小。因此，通過算法1能夠有效地搜索出帕累托最優解。以CE 模型[4]和SRGAN 模型[7]為例，這兩種模型只包含兩種損失，采用式（6）確定的權重參數，與使用交叉驗證的方式獲得的權重參數，對GANs模型產生了相當的性能影響。但是算法1不需要繁瑣的交叉驗證，能夠進一步縮短訓練時間。

2.2 多目標帕累托最優解（K＞2）

K=1 或K=2 可以看作多目標GANs優化的特例，而K ＞2 是多目標GANs 優化的一般情況。當K ＞2時，采用常見的交叉驗證方法確定權重參數非常耗時。隨著目標數量的增加，驗證過程的耗時情況幾乎呈指數增長。同時目標數量的增加，目標之間的“沖突”情況更復雜；參數維度較高，直接應用線性搜索算法容易陷入局部最優。基于MGDA算法，所提算法將多目標GANs優化問題分解為多個兩目標優化，確定最優權重參數之后，再沿著的方向使用線性搜索來獲取帕累托最優解。具體如算法2所示。

算法2多目標帕累托最優解算法

此時，GANs 模型達到最優狀態，各項損失不再變化，梯度不再更新。因此，α={α1,α2,…,αK}即為式（4）的最優權重參數，并且當前參數為該式的最優解。

其中，λ=1-ω 是常數，ω 表示固定權重參數的和。

綜上所述，多目標GANs 優化取決于特定的目標數，當K=2 時，采用算法1進行優化求解；當K＞2 時，采用算法2進行優化求解。

3 實驗結果

為了驗證算法1 和算法2 在實際應用中的有效性，主要對比兩種權重參數確定方式以及對圖像任務的性能差異：

方式1利用交叉驗證方法確定權重參數；

方式2利用算法1或算法2確定權重參數。

對比算法涉及圖像修復，圖像超分辨，圖像-圖像轉換和圖像哈希檢索等多個領域。具體算法包括：CE[4]、SRGAN[7]、RankSRGAN[8]、BicycleGAN[12]、SNSR-GAN[13]和BGAN[15]。進行實驗對比時，采用原文獻提供的數據集和源代碼，所提算法和所有對比算法的仿真實驗建立在“四核Intel?Core?i-7685K CPU @3.6 GHz”處理器和四塊“NVIDIA Titan V”的硬件環境上。

為了直觀展示算法1 和算法2 的優勢，選擇PSNR和SSIM 收斂情況進行對比，所有模型重復訓練500次。PSNR和SSIM的定義分別如下：

其中，M和N分別表示圖像的大小，I(x,y)和I*(x,y)分別表示原始圖像和變換圖像。Max(I(x,y))表示原始圖像中最大的像素值[30]。

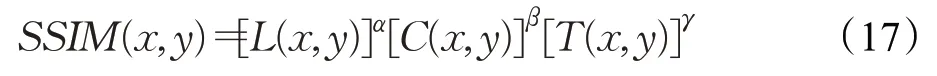
其中，L(x,y)表示亮度函數，C(x,y)表示對比度函數，T(x,y)表示結構函數。α、β和γ表示對應函數的權重[30]。

根據目標數（損失項數量），將從以下三方面討論所提算法的有效性。

3.1 K=2

本節實驗主要對比CE 模型[4]和SRGAN 模型[7]，這兩種模型均包含兩種損失函數，即，K=2。CE模型包含對抗損失和重建損失（L范數），SRGAN 模型包含對抗損失和內容損失。盡管內容損失還包括MSE 損失（Mean Square Error，MSE）和視覺感知損失，但二者權重相同，可以認定SRGAN 只包含兩種損失。實驗結果對比如圖2、圖3所示。

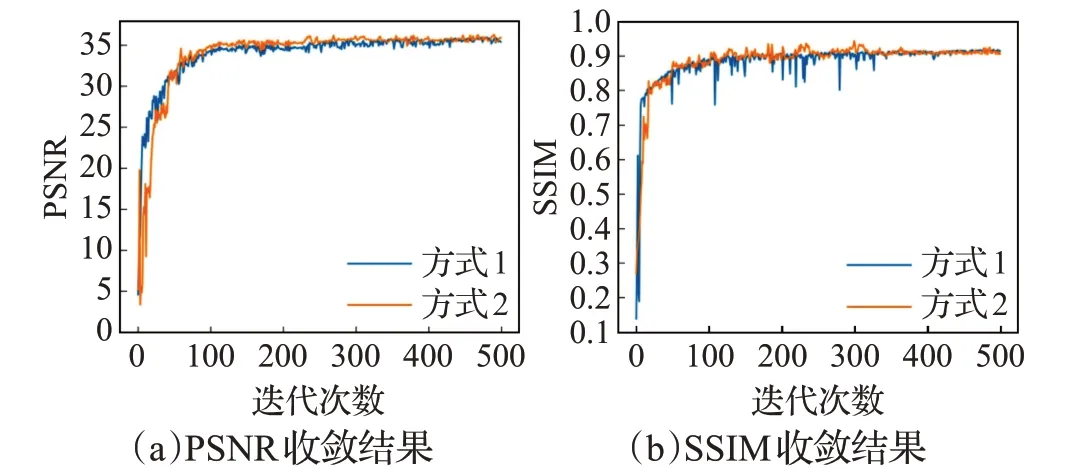
圖2 方式1、方式2在CE模型上的性能對比

圖3 方式1、方式2在SRGAN模型上的性能對比

圖2、圖3 顯示，采用算法1 確定的權重參數與原文采用交叉驗證方法確定的權重參數，對模型的整體性能影響相當，二者都能產生較好的實驗效果。但是在實際訓練過程中，算法1 耗時少，可操作性和參數自適應更強。

3.2 K＞2

本節實驗主要對比RankSRGAN[8]、BicycleGAN[12]和BGAN[13]模型，這三種模型的目標數分別為：K=3、K=4 和K=5。如前文分析，由于目標數較多，采用交叉驗證確定權重參數異常耗時。因此，實驗直接采用原文中的權重參數和訓練數據集。實驗結果對比如圖4～6所示。

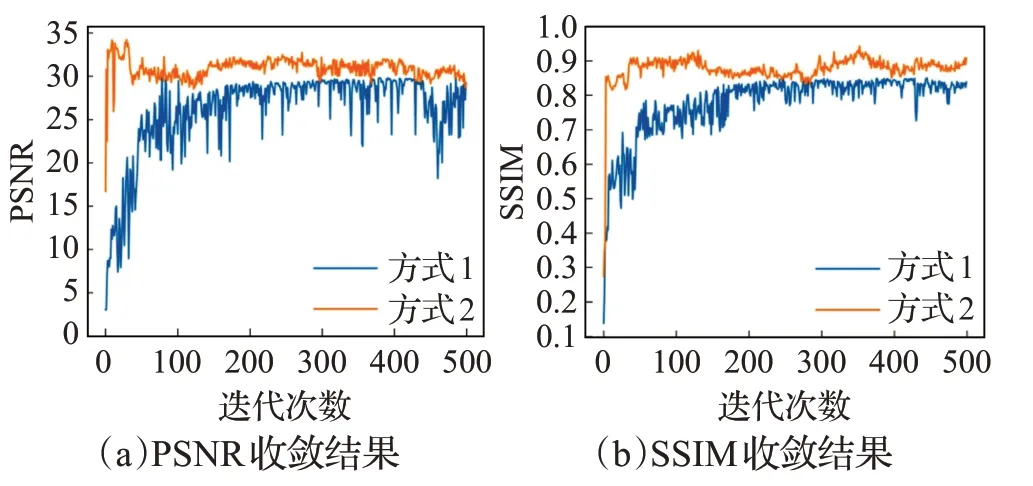
圖4 方式1、方式2在RankSRGAN模型上的性能對比

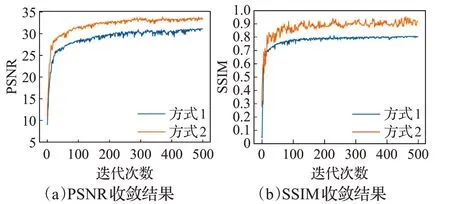
圖5 方式1、方式2在BicycleGAN模型上的性能對比

圖6 方式1、方式2在BGAN模型上的性能對比

圖4～6 顯示，當K＞2 時，對比交叉驗證，算法2 具有明顯的優勢，并且目標數量越多，產生的優勢越明顯。此外，結合圖2～6 可以看出，采用方式1 訓練的模型，獲得的PSNR或SSIM值收斂性較差，這間接地說明了采用方式1確定權重參數并非最優權重，同時也說明了對于權重參數敏感的模型而言，非最優權重參數對模型的性能影響較大。

3.3 K＞2但部分權重參數固定

本節實驗選擇SNSR-GAN 模型[13]進行驗證。該模型包含6種目標，但為保證病理不變性和保持醫學圖像的邊緣信息，根據先驗知識，設置了其中3個權重參數，即，該模型中的部分權重參數是確定的。此時，需要將算法2中的步驟8替換為式（15）。實驗對比結果如圖7所示。圖7顯示，對于多目標優化任務并且部分權重參數確定的情況，所提算法仍能產生較好的實驗結果。

圖7 方式1、方式2在SNSR-GAN模型上的性能對比

為比較所提算法與交叉驗證方法的計算耗時情況，本文根據文獻[4，7-8，12-13，15]提供的源碼，估計獲取最優參數的時間。結果如表1所示。

表1 交叉驗證與所提算法計算耗時對比

結合圖2～7 和表1 的實驗結果可以看出，當不確定權重參數的數量等于2 時，方式1 和方式2 產生相當的實驗結果，但所提算法可操作性和參數自適應性更強，耗時更少；當不確定權重參數的數量大于2 時，本文所提算法能夠產生更好的實驗結果，同時耗時少，可操作性、自適應性強。

4 結束語

為了優化多目標生成對抗網絡及求得帕累托最優解，本文基于梯度策略，將多目標優化分解為多個兩目標優化，提出帕累托最優解求解算法，較好地解決了求解多目標、高維度生成對抗網絡最優解的NP 難問題。此外，將所提算法應用到多個圖像子領域，實驗結果進一步驗證了所提算法的有效性。實驗結果顯示，即使部分參數權重確定，只要模型的待確定參數權重大于2，所提算法具有明顯的性能和計算優勢。在訓練和更新深度神經網絡時，由于梯度反向計算和更新比前向計算更耗時，導致整個算法比其他基于梯度策略的方法耗時。算法的耗時仍是文章值得改進的地方，這也是下一步的研究重點。