可調拱梁穩定性分析 *

徐錦元，張政武

(陜西理工大學 機械工程學院， 陜西 漢中 723000)

0 引 言

在建筑、交通、水利等領域常見的設備結構中，幾乎所有板件、構件與整體結構的受壓部位，都會涉及穩定問題，其中鋼結構因材料強度高，結構組件纖薄，通常在強度破壞之前便容易發生整體失穩或局部失穩[1]。

國內文獻針對拱梁結構穩定性問題的研究對象通常為拱橋或拱壩結構，如邵旭東等[2]提出了一種特大跨徑鋼-UHPC組合桁式拱橋新體系，并驗證了其各施工階段的穩定性、剛度與強度等使用要求；呂征等[3]以中國某300 m級高拱壩為研究對象，設計了兩種方案回填混凝土，然后對兩種方案進行了超載能力與穩定性的驗證；馬坤全等[4]針對鐵路拱橋拱梁結合部局部結構的復雜性，建立了精細化模型進行了剛強度分析與穩定性分析；呂君等[5]介紹了拱壩抗剪安全度分析評估方法與整體穩定分析方法及其失穩依據，探討了拱壩最不利截面抗剪強度指標值；尤吉等[6]提出了一種通透肋式連拱榜山隧道結構，并通過有限元方法對其變形受力特征及結構穩定性進行了分析，證明了設計方案的可行性，為該類隧道結構提供了新思路；李杰等[7]為探究異性拱梁穩定性，利用有限元方法分析了鋼箱拱肋板厚、橫撐、梁拱剛度對結構穩定性的敏感性；謝肖禮等[8]通過增加剛性斜桿與拱肋及主梁節段形成三角形結構，大幅增加了拱梁固結拱橋整體剛度并增強了其穩定性。而對于非拱橋或拱壩為對象的拱梁結構穩定性研究問題多見于外文文獻，如Rawlilson O. Araújo等[9]證明了圓拱形梁振動的數學模型Bresse系統與其漸進穩定性有關，在此基礎上模擬了具有記憶效應的拱形梁，建立了外力作用下能量的衰減率；Liu TianQiao等[10]基于最新的彎曲拉擠成型技術，開發了GFRP拱形梁結構，通過對梁的屈曲分析與破壞試驗證實了GFRP拱形梁的巨大潛力。

TC4635-Q型鋼模臺車是一種曲線段可變式鋼模臺車，可以完成臺車4～6 m變高、3～5 m變跨及由變跨引起的變弧，可調拱梁在該臺車中負責傳遞外載荷與增加拱部剛度，并且能夠適應不同拱形和跨度范圍內拱頂圓弧的調節，其結構的穩定性對于臺車整體安全性能十分重要。為探究其穩定性，首先介紹了拱梁結構組成，按照其尺寸參數進行了三維建模，并計算出實際工況下拱梁所承受的外載荷與在外載荷下拱梁的剛、強度，然后將結構強度最不利部位簡化為兩餃拱計算出屈曲載荷，與通過ANSYS分析整體結構屈曲載荷對比驗證了拱梁的穩定性，最后探究了臺車跨度變為4 m、5 m與6 m時拱跨、拱高與兩千斤支撐間距三組結構參數對可調拱梁整體穩定性的影響，研究結果為拱梁結構的設計與分析提供了一定的理論參考。

1 可調拱梁結構介紹與建模

TC4635-Q型鋼模臺車主要由模板系統、框架系統與電液系統等組成。框架系統通過伸縮油缸推動橫梁外套左右移動實現臺車4～6 m變跨，頂升油缸推動臺車立柱中套與外套實現3～5 m變高，由變跨引起的變弧通過可調拱梁實現。該鋼模臺車由兩個約6 m長的單元節組成，每個單元節前后兩端各有一組、中間均勻分布四組可調拱梁。臺車最大跨度為6 m時，一組可調拱梁結構如圖1所示。

圖1 可調拱梁二維結構1.側模板 2.拱頂模板 3.固定三角形塊 4.可調絲杠 5.可調三角形塊 6.連接銷軸 7.框架系統 8.縱梁 9.人字千斤

每組可調拱梁由位于中間的一個可調三角形塊5與其余若干個固定三角形塊3組成，三角形塊下端由可調絲杠4連接，上端由連接銷軸6首尾鉸接，拱頂模板2固定在可調拱梁上表面，兩端與側模板1連接，拱梁兩側通過兩組人字千斤9支撐于框架系統7的縱梁8上。由變跨引起拱頂弧度變化時，可調拱梁首先取下可調三角形塊，將拱梁分為左右兩部分，從兩邊向中間依次調整絲杠長度并根據實際跨距增減固定三角形塊與絲杠數量，直至將整個裝置調節至實際位置，完成變弧。

結合圖1拱梁二維結構，6 m跨可調拱梁尺寸參數如表1所列。表中：L為拱梁跨度；L1為梁人字千斤支撐間距；L2位拱梁總弧長；H為拱高；h為千斤支撐點與頂點距離；s為拱寬；r為拱梁弧半徑。

基于可調拱梁的二維結構與尺寸參數，利用CREO軟件建立可調拱梁三維模型，如圖2所示。

表1 6 m跨可調拱梁尺寸參數表/m

圖2 可調拱梁三維模型

2 拱梁靜力學分析

分析可調拱梁穩定性需計算拱梁靜力解[1]。可調拱梁材料為Q235鋼，其參數如表2所列。

表2 Q235鋼材料參數表

可調拱梁所受外載荷來源于拱頂模板，根據規范[11]臺車拱頂模板所承受載荷主要包括頂部混凝土自重載荷與局部擠壓面載荷。臺車在跨度6 m時的實際工況下，拱梁所承受外載荷的計算如表3所列。

表3 可調拱梁外載荷計算公式與結果

將可調拱梁模型導入ANSYS workbench軟件進行靜力學分析，設置模型材料與劃分網格后，根據實際工況下可調拱梁受力情況，將拱梁兩端底面與人字千斤底面固定約束，在拱梁上表面施加外載荷P，求解模型得到拱梁位移云圖與應力云圖如圖3所示。

圖3 拱梁應力應變云圖

由3(a)位移云圖可知拱梁最大變形處于拱梁頂端受力處，最大高度降低約1.807 4 mm，小于拱梁最大允許位移[l]=l/1000=6.954 mm(l為拱梁長度)，滿足拱梁強度使用要求；由3(b)應力云圖可知拱梁結構除去部分應力集中外的整體應力約20.361 MPa，小于材料許用應力215 MPa，滿足拱梁剛度使用要求。

3 拱梁穩定性分析

結構穩定性分析理論計算方法一般有針對未變形結構平衡方程的一階分析法與基于已變形結構幾何關系的二階分析法兩種，相應的ANSYS workbench平臺提供兩種結構穩定性分析模塊分別為針對理想物體的特征值屈曲分析與考慮初始缺陷的非線性屈曲分析[1]。

3.1 拱梁屈曲載荷理論計算

由圖3拱梁靜力學分析結果可知，拱梁結構最危險部位主要處于兩組人字千斤支撐之間，將連接相鄰兩組三角形塊的連接看作拱平面外等間距支撐，則弧拱只發生平面內失穩[12]。將兩組人字千斤支撐看作弧拱兩端，中間部分則為純壓兩餃拱，其理論模型如圖4所示。

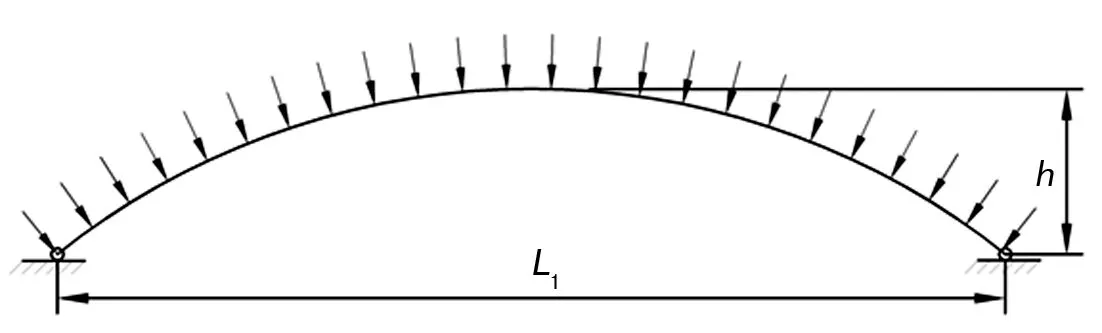
圖4 拱梁理論模型

結合《拱形鋼結構技術規程》[13]中純壓圓弧兩餃拱平面內屈曲載荷計算公式，計算兩餃拱矢跨比、拱截面慣性矩以及兩餃拱屈曲載荷qcr結果如表4所示。

表4 兩餃拱平面內屈曲載荷計算公式與結果

3.2 ANSYS workbench屈曲分析

將外載荷設置為1 MPa的拱梁靜力分析結果導入特征值屈曲分析模塊[15]，求解得到拱梁模型在理想狀態下的一階屈曲模態云圖如圖5所示，從云圖中可以看出模型屈曲特征值為3.383 9，可知拱梁特征值屈曲載荷為3.383 9 MPa。

設置初始缺陷因子為10%，通過特征值一階屈曲模態生成含初始缺陷的可調拱梁模型[16]，導入靜力學求解模塊進行非線性屈曲分析，其中拱梁外載荷設置需大于特征值屈曲載荷[17]，文中設為5 MPa，通過自動迭代131步后，提取出拱梁外載荷迭代值與對應最大位移曲線圖如圖6所示。

由圖6可看出，拱梁模型在外載荷為0～2.95 MPa時，外載荷與位移呈正比，在外載荷增加至2.95 MPa時，拱梁發生屈曲，此時拱梁結構位移達到最大21.59 mm，隨著外載荷的繼續增大，模型發生失穩。

圖5 拱梁特征值屈曲位移云圖

圖6 拱梁外載荷與位移曲線圖

由此可知，非線性屈曲分析所得屈曲載荷為2.95 MPa，與特征值屈曲載荷相比小12.8%，顯然通過非線性屈曲分析所得屈曲載荷更為精確。

3.3 理論計算與ANSYS分析結果對比

由表4可知，拱梁理論模型即兩組人字千斤支撐中間區域計算出的拱梁危險部位屈曲載荷為2.47 MPa，與ANSYS workbench軟件非線性屈曲分析計算所得拱梁非線性屈曲載荷2.95 MPa作對比，知兩結果相差16.27%，考慮到理論計算模型僅選擇兩組人字千斤之間部分，且將可調拱梁截面模型近似看作箱型結構，故誤差在合理范圍之內，驗證了軟件分析結果的合理性，又由于該分析結果遠大于拱梁在實際工況下的外載荷0.0103 MPa，可以證明可調拱梁具有良好的穩定性。

4 拱梁尺寸參數對屈曲載荷敏感分析

在鋼模臺車變跨時，可調拱梁部分尺寸參數會隨之發生變化，為了保證變跨時拱梁的穩定性，選擇由部分代替全面而得到全面試驗情況的正交試驗設計方法，分析拱梁尺寸參數對結構穩定性的影響。研究臺車變跨時可調拱梁結構變化，拱梁矢跨比與千斤支撐間距對整體穩定性有較大的影響，選擇拱梁跨度、拱高與兩組人字千斤間距三組尺寸參數為試驗因素，其中拱梁跨度分別為4 m、5 m及6 m時拱高與千斤間距的尺寸作為因素的水平數，得到正交試驗因素水平配置如表5所列。

表5 拱梁尺寸參數水平配置表 /m

根據三因素三水平配置表選擇正交試驗表L9(33)計算[18]，并對結果數據進行分析如表6所列。表中：Ki為該因素在i水平結果的和；ki為對應Ki的均值；R為ki最大值與最小值之差。

表6 L9(33)正交試驗計算結果及分析

極差R越大所對應因素越重要[19]，由表6可知，三組因素重要性排序為：拱跨>間距>拱高，并且隨著拱梁跨度、間距及拱高的增大，拱梁屈曲載荷逐漸變小，拱梁越不穩定。考慮交互作用影響，避免仿真實驗誤差，準確檢驗三組尺寸參數對屈曲載荷影響的顯著程度，對表6數據進行方差分析，結果如表7所列。

表7 方差分析結果

F值越大說明因素對結果的影響越大[19]，結合表7分析結果可知，三組結構參數對結構屈曲載荷的影響性排序與表6結果相同。p值小于0.1，則代表該因素與結果存在一定的顯著性差異關系[20]，由表7可知，拱跨對屈曲載荷的影響存在一定顯著性，拱高與拱寬為非顯著因素，對屈曲載荷影響較小。

5 結 語

以可調拱梁為研究對象，為探究其結構穩定問題與影響拱梁結構穩定性的主要因素，首先介紹了可調拱梁主要結構并按照跨度最大6 m的拱梁結構尺寸參數建立了可調拱梁三維模型，之后計算出拱梁在實際工況下的外載荷為0.0103 MPa，對其進行靜力學分析，結果說明模型最大變形處于頂部中間，為1.807 4 mm，符合強度使用要求；然后，簡化強度最不利區域為純壓圓弧兩餃拱，計算出其屈曲載荷為2.47 MPa，并與通過ANSYS軟件分析計算出的屈曲載荷2.95 MPa相比誤差為16.27%，處于合理范圍內，驗證出可調拱梁具有良好的穩定性；最后，為探究臺車變跨時拱梁尺寸參數對屈曲載荷的影響性，選擇拱跨、拱高與兩千斤支撐間距三組結構參數作為可變因素，拱梁屈曲載荷為結果，進行三因素三水平正交試驗，通過對試驗數據分析說明三組結構尺寸參數與屈曲載荷呈負相關，并且其影響性大小排序為：拱跨>千斤間距>拱高，拱跨對結構屈曲載荷的影響存在一定顯著性。希望對拱梁結構之后的設計研究有一定的參考價值。