軌道交通車輛單元制動器停放制動力補償方案及其優化計算 *

虞曉峰，余毅權

(南京中車浦鎮海泰制動設備有限公司，江蘇 南京 211800)

0 引 言

軌道交通車輛須在無壓縮空氣狀態下進行車輛停放制動，通常采用裝備了儲能彈簧的單元制動器進行停放力輸出。由于單元制動器空間受限，須采用高應力、大載荷(剛度較大)的儲能彈簧，該彈簧輸出力值隨工作行程的變大而降低。單元制動器在生產及使用過程中難免出現尺寸偏差、彈性變形、機械磨損、制動摩擦副磨耗補償異常等造成儲能彈簧工作高度不穩定的現象。因此，單元制動器的停放力值也常不穩定。筆者提出一種采用弧線代替傳統直線作為楔形放大作用線并進行彈簧力值因行程影響導致降低而補償的設計方法和具體計算過程，該方法可有效改善單元制動器停放制動力值不穩定的現象，達到設計目標。

1 作用原理

單元制動器作為軌道交通車輛的制動執行機構，其摩擦副間隙通常設置為3～6 mm。單元制動器具有磨耗自動補償功能，正常情況下，其制動盤與閘片的間隙均穩定處于3～6 mm范圍內，但實際使用過程中也存在偏離目標范圍的情況，其間隙變化尤其對停放制動力影響較大。如圖1所示，一種采用儲能彈簧的單元制動器停放機構，停放缸排氣釋放彈簧，彈簧驅動楔形拉桿，垂向彈簧力值被楔形拉桿傳遞至橫向的制動套筒最終傳遞給摩擦副產生停放制動。為充分利用車下空間，降低彈簧設計應力，通常采用楔形放大機構將彈簧輸出力進行放大后使用。

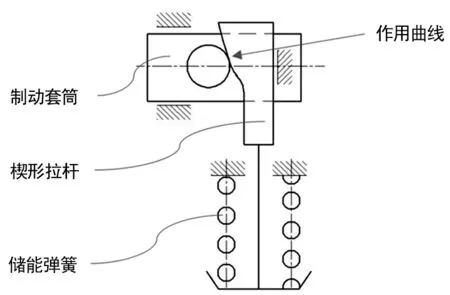
圖1 停放機構原理簡圖

傳統方法是采用直線作為放大作用曲線，放大倍率即為1/tanθ(θ<90°)，θ為滾子與楔形拉桿接觸點的切向角度(作用直線與垂直方向角度)，隨著彈簧工作高度增大，彈簧力值降低(彈簧輸出呈線性)，相應的放大機構輸出力也隨之降低。而采用弧線代替直線后，隨著彈簧工作高度增大，切向角度θ變小，放大倍率1/tanθ將增大，對放大機構的輸出力進行一定的補償。但因為彈簧輸出力在降低、放大倍率在增加，機構輸出力的最終大小仍和作用曲線存在重要關聯。因此，研究作用曲線及其作用效果顯得十分必要。

2 輸出力計算及優化分析

停放制動力的計算可根據機構設計的空間尺寸進行初步確定曲線參數，充分考慮機構彈性變形、尺寸偏差等影響因子，利用Excel工具進行公式化迭代計算，結合計算結果，反向計算曲線半徑，采用CAD繪圖幾何方法進一步優化楔形放大機構的作用曲線，過程如圖2所示。

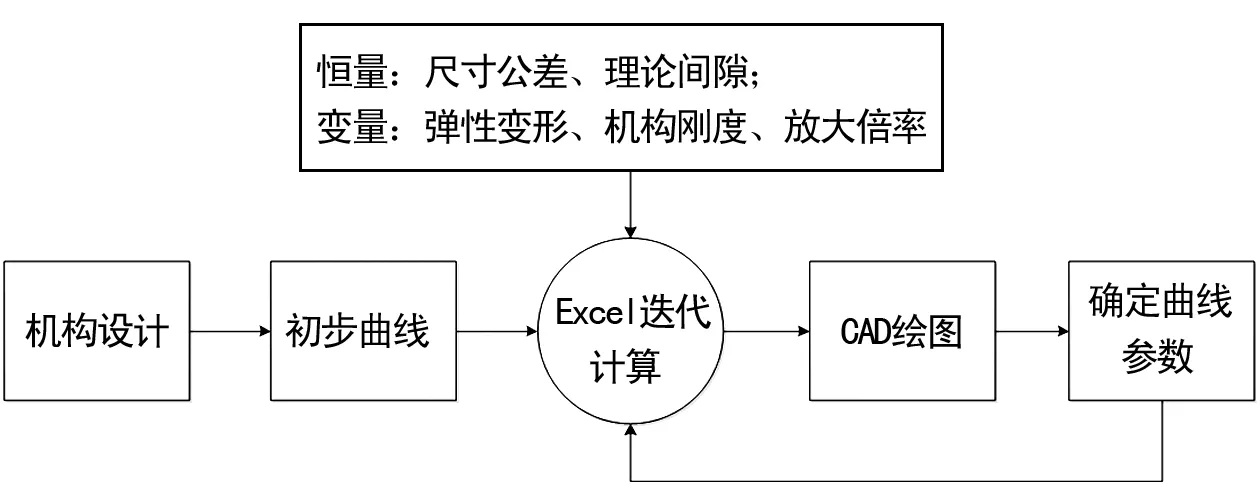
圖2 計算過程

2.1 輸出力計算

套筒滾子在楔形拉桿作用曲線上運動時，受力方向隨著作用曲線變化而變化，作用曲線由Ⅰ段、Ⅱ段組成。為便于闡述過程，對作用曲線進行了幾何尺寸標注和定義，如圖3所示。

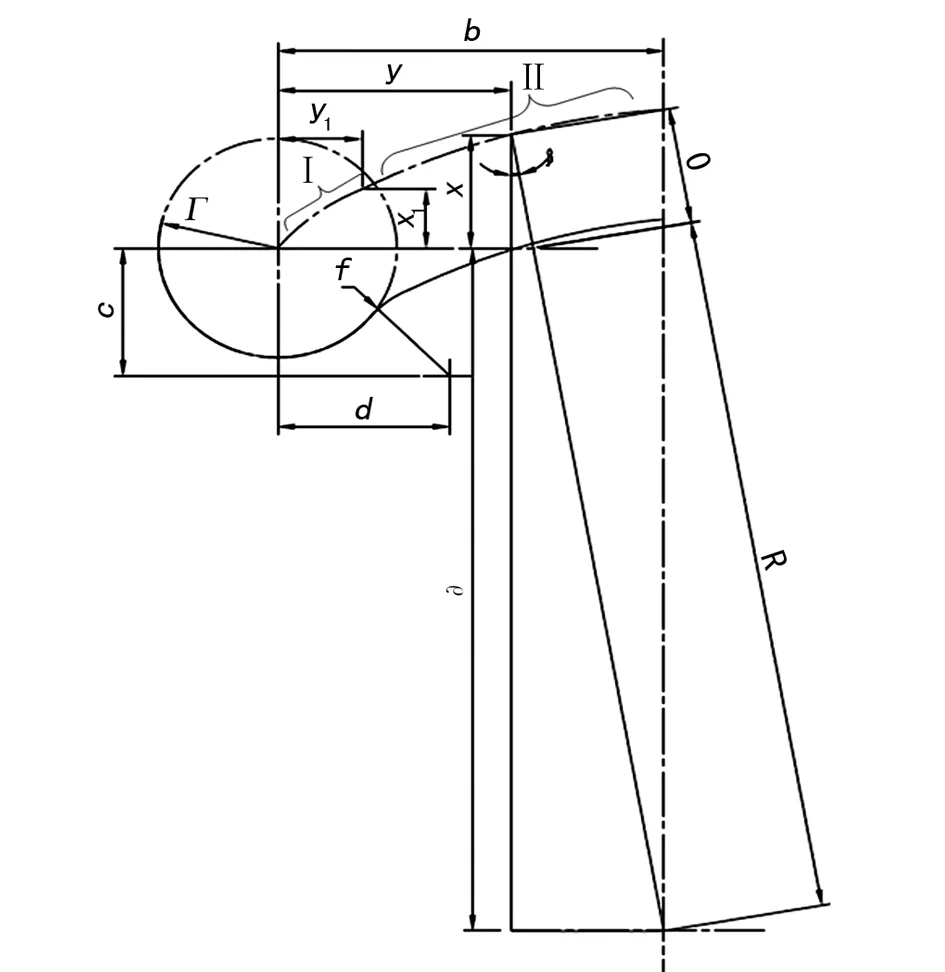
圖3 幾何關系圖

(1) 放大倍率計算 為了縮短停放制動行程，楔形塊設計為分段曲線，第Ⅰ段為快速制動行程，第Ⅱ段為工作行程，分界點為坐標為(x1，y1)，如圖3所示。因快速制動行程非工作面，此處不進行分析。根據工作原理，x為停放制動行程，y停放彈簧伸長量，由幾何關系楔形塊的放大倍率i與停放制動行程x由如下關系：

當停放制動行程大于x1(mm)時，停放倍率表達式為：

(1)

(2) 彈簧伸長量 根據圖3幾何關系，停放制動行程x與停放彈簧伸長量y有如下關系：

當停放制動行程大于x1時，停放彈簧伸長量y表達式為：

(2)

(3) 輸出力計算 將機構部件的尺寸公差累計間隙進行分析計算得到衡量值Δ1；

將機構部件進行有限元分析計算，可得出機構剛度δ，即可得到彈性變形Δ2，其與彈簧輸出力Fw基本成線性關系，因此有：

Δ2=Fw×δ

制動器的緩解間隙S，停放制動行程x：

x=S+Δ1+Δ2

(3)

彈簧設計剛度k，對應的彈簧輸出力為：

Fw=F0-y×k

(4)

當制動器處于理論間隙為S0(mm)時，停放制動行程x、彈簧的輸出力Fw、放大倍率i三個參數相互影響，此處對式(1)～(4)進行迭代計算，即可確定Fw及i。

根據制動單元工作原理不難得出理論間隙為S0(mm)時停放制動力(α、β、γ為常數)：

FP=(FW+α)×i×β+γ

(5)

2.2 優化分析

由上述計算過程及結果可知，不同的理論間隙S0可算得出不同的x、Fw、i及FP。在產品設計中，優化目標是停放制動力值FP保持恒定，而FP保持恒定的關鍵在于作用曲線的設計。

在一款帶停放單元制動器設計中，根據機構尺寸及空間，初步確定以下關鍵輸入參數，見表1。

表1 初步確定參數

采用EXCEL工具將式(1)～(5)進行公式化，分別計算3～6 mm范圍內(按0.1 mm遞進)的Fw、i及FP，將計算結果進行圖表化分析，如圖4所示。

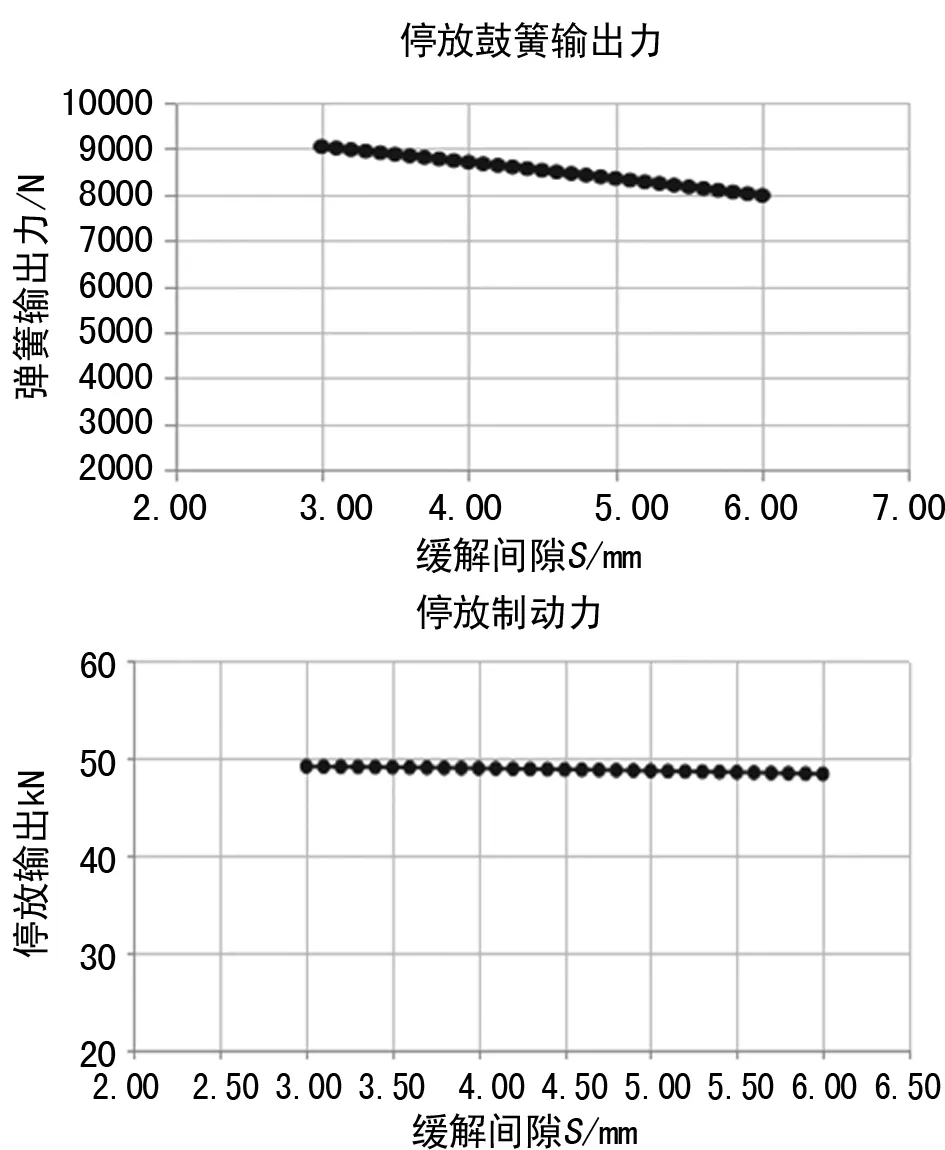
圖4 停放制動力初步計算結果

由圖4可知，既有作用曲線具有明顯放大作用且具有一定補償作用，但隨著緩解間隙增大，停放制動力出現了小幅下降。

針對上述結果，結合圖3幾何關系，取優化目標停放制動力Fw值為50 kN恒定值(力值大小取決于車輛停放制動需求)，根據式(5)，可得出相應的放大倍率i值，再根據式(1)，即可計算出不同緩解間隙下的曲線半徑R值。此時計算所得的R值可認為是目標曲線位置近似圓的半徑。

借助于CAD工具分別以(緩解間隙初始值、中間值、最大值)3 mm、4.5 mm及6 mm時的y值作直線，確定停放彈簧工作高度。以三點不同位置對應R值為半徑、圓心不變作圓，分別與三條直線相交形成3個模擬接觸點，再分別以上述3接觸點確定圓，該圓即為目標作用曲線的理論輪廓。重新量取作用曲線的參數，如表2所列。

將優化后的作用曲線參數帶入上述計算公式進行輸出力計算，不同緩解間隙對應停放制動力的結果如圖5所示。

表2 優化參數取值 /mm

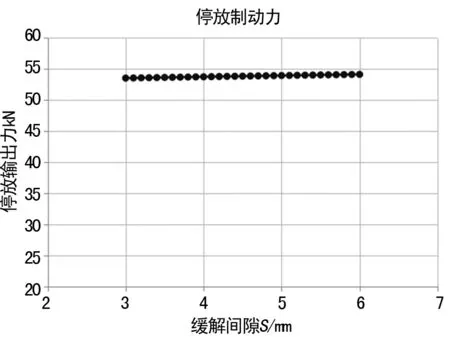
圖5 優化后的停放制動力初步計算結果

對比圖4、5，優化后的停放制動力明顯增加，并且力值下降趨勢明顯改善。

3 結 語

上述關于軌道交通車輛單元制動器產品設計中補償停放制動力衰減的設計方案及其計算方法,能夠根據設計目標要求，考慮機構剛度、尺寸公差等多種影響因子，進行較為精確的停放制動力的計算，根據計算結果，采用幾何方法進一步優化楔形放大機構的作用曲線。經過對產品停放制動力進行測試，結果表明隨著緩解間隙的增加，停放輸出力不再下降，補償方案及優化計算明顯有效。文中提及的方案及計算在類似產品設計中具有重要的指導意義。