基于模糊實物期權的獨角獸企業價值評估

谷錦錦 李志剛

(成都理工大學 管理科學學院，四川 成都 610059)

0 引言

獨角獸企業由美國著名投資人Aileen Lee于2013年提出，指那些發展速度快、數量稀少、投資者青睞的初創企業[1]，在全球范圍內得到企業界和投資界的追捧[2]。面對獨角獸企業發展需求，正確評估獨角獸企業價值成為政府和投資者共同關注的話題。因此，建立一套獨角獸企業價值評估體系是十分必要。

獨角獸企業價值評估屬于企業價值評估的研究領域。與傳統企業相比，獨角獸企業具有高風險性和高收益性、成長周期短，無形資產在企業中所占比重較高、科研研發投入所占比重較大、無法產生穩定現金流等典型特征。因此，傳統的企業價值評估方法并不適用于獨角獸企業價值評估。對此一些學者對獨角獸企業價值評估方法進行了探討。如利用經濟增加值(REVA)法、利益相關者博弈、實物期權理論、梅特卡夫估值模型等。其中實物期權理論及其方法針對無穩定現金流、具有高度成長性等企業，可以量化資產價值變動的隨機性，較好反映企業未來價值增長潛力[3-5]。但是常見的B-S期權定價模型在進行定價的時候涉及到的參數需要精確數值，具有局限性[6]。模糊集合理論提供了對模糊現象進行定量處理和分析運算的方法[5]。一些學者將模糊理論引入到實物期權估值中，將企業標的資產、執行價格、現金流、投資成本和無風險利率等參數設置為模糊數，建立了模糊實物期權評價模型[7, 8]。這對B-S定價模型進行了改進，使企業價值評估值處在一定變動范圍內，使評估結果更具合理性[9]。

本文將模糊理論與實物期權理論相結合，提出一種基于模糊實物期權的獨角獸企業價值評估方法。這不是對傳統的價值評估方法的否定，而是在傳統方法的基礎上，找出更適合獨角獸企業價值評估的方法。為今后研究獨角獸企業價值提供了全新的觀察視角和研究思路。

1 模糊理論

模糊數理論是Zadeh在1965年首次提出，用來解決那些含義較模糊、不能量化、界限不清晰變量的一種數學方法[10]。其核心是通過隸屬函數打破普通集合論中元素對集合的絕對隸屬關系。例如給定域U上的一個模糊集，是指對任何y∈U都有一個數u(y)∈[0,1]和它相對應，u(y)稱為y對U的隸屬度，u稱為y的隸屬函數。

模糊數一般分為梯形模糊數和三角模糊數和不規則模糊數，本文所示為梯形模糊數，三角模糊數是梯形模糊數m1=m2的特殊情況，過于簡單與獨角獸企業面臨的實際情況不相符，不規則模糊數計算又過于復雜。而梯形模糊數不僅能夠將獨角獸企業的不確定性較好的體現出來，且運算較為簡便，能與實物期權模型更好結合，計算出更為準確的期權價值。因此，本文選取梯形模糊數來構建模糊實物期權模型，進行獨角獸企業價值的評估。

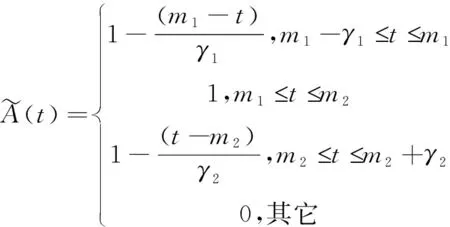
(1)

圖1 模糊梯形函數

梯形迷糊數的計算特征有：

(2)

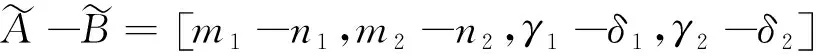
(3)

(4)

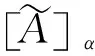
均值為：

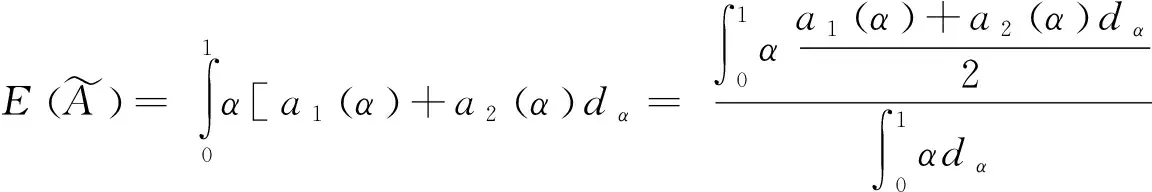
(5)

其均值為：

(6)

方差：

(7)

(8)

其中，波動率為：

(9)

2 模糊實物期權模型

實物期權定價模型主要有連續時間下的B-S模型和離散時間下的二叉樹模型。當離散時間間隔趨向無窮小時，可從二叉樹模型推導出B-S模型。由于，B-S模型計算實物期權時比較簡單，可操作性強，在現實中的應用較為廣泛。因此，本文選擇B-S模型。

2.1 B-S期權定價模型

B-S期權定價模型由FisherBlock和MyronScholes在1973提出。它的基本假設條件主要有：期權交易中不含稅收以及交易成本；標的金融資產在有效期內無紅利發放；在期權壽命期內，股票價格遵循幾何布朗運動；在期權有效期內無風險利率是保持不變的；期權為歐式期權；允許賣空和買空期權；證券市場上的交易是連續發生的。

B-S期權定價模型的基本表達式為：

(10)

式(9)中，C表示歐式看漲期權的價格；S表示標的資產現行價值；X表示行使期權的執行價格；T表示期權有效時間；r表示有效期的無風險利率；N(x)表示標準正態分布變量的累計概率分布函數；σ表示標的資產收益波動率；e為自然對數的底數。

2.2 模糊參數分析

采用實物期權定價方法可量化資產價值變動的隨機性，較好反映獨角獸企業未來價值增長潛力。然而，由于假設條件嚴格、估值參數常為固定值。而在實際應用中，企業價值評估受到諸多不確定因素的影響，其估值參數在一定區間內變化，并非是一個固定數值。

一些學者研究發現標的資產現行價值(S)、期權到期的執行價格(X)兩個參數對實物期權定價模型影響較大，其他三個單因素變量對專利期權價值的影響相對較小，如圖2所示。因此，本文將對標的資產的現行價值(S)、期權到期的執行價格(X)兩個參數進行模糊化處理。

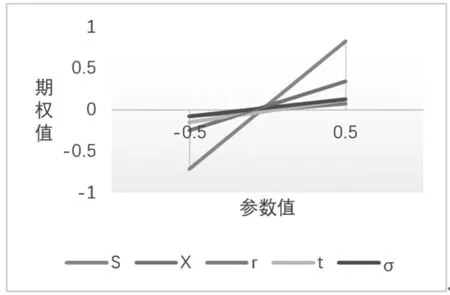
圖2 五個參數對B-S實物期權值的影響

2.3 模糊實物期權定價模型

根據模糊數的相關運算法則，則模糊實物期權為：

(11)

根據梯形模糊數的運算可得獨角獸企業價值模糊實物期權為：

1)商品分類瀏覽、商品搜索功能實現如圖1，左邊的分類欄可供用戶選擇不同類型的商品，右邊則為商品的展示，同時還有個分頁的實現。在商品的展示上面就是商品搜索功能，用戶可以直入主題，過濾掉不喜歡的，尋找自己想要的閑置物品。

FROV=(FROV1,FROV2,γ1,γ2)

(12)

其中：

(13)

(14)

(15)

(16)

企業整體價值=標的資產的現行價值+模糊實物期權價值

(17)

3 實證分析

3.1 實證對象的選擇

A企業是一個具有代表性的超級“獨角獸”企業，在2014年上市，截至2019年12月20日，其市值為5700億美元，旗下許多企業同樣是“獨角獸”企業，相比其他“獨角獸”企業相對成熟。因此，本文以A企業為例進行說明。A企業主要業務包括：電商、云計算、數字媒體和娛樂以及創新項目和其他業務。對于這樣一個互聯網公司而言，未來成長空間廣闊。但行業的波動性及不確定性也大，用模糊實物期權的方法來評估該企業價值是合理的選擇。

3.2 數據收集與計算

可得：

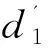
最后將上述計算的結果帶入到企業價值評估模糊實物期權價值公式(12)中，可以得到：

FROV=(FROV1,FROV2,γ1,γ2)=(441.196，628.806，292.453，518.676)

其中:

因此，可以得到A企業在2019年期末的期權價值最有可能的理論區間為(441.196，647.865)(億元)。最大區間為為(148.832，1166.533)(億元)。

根據前文提到的包含實物期權的企業整體價值為：

企業整體價值=標的資產的現行價值+模糊實物期權價值

最終可以得出企業整體價值最有可能的理論區間為(1406.272,1612.941)(億元)。最大區間為(1113.908，2131.609)(億元)。

4 結語

研究結果表明，模糊數的引入克服了B-S 模型參數的主觀模糊性，降低了對參數精確性的要求。使模糊環境下獨角獸企業估值具有可控性，從而更合理地評估獨角獸企業的價值，為今后研究獨角獸企業價值提供了觀察視角和研究思路。