利用BP神經網絡對衛星無熱敏設備溫度的估測
寧東坡,徐志明,劉質加
中國空間技術研究院,北京 100094
隨著航天技術的發展,小衛星在遙感、減災、農業等方面的應用越來越廣泛。衛星在太空中繞軌道運行,太空熱環境惡劣,衛星主要會受到太陽輻射、地球反照和地球紅外輻射外熱源影響,因此必須進行專門的熱控設計保障衛星正常工作[1]。
為監測衛星設備溫度,熱控設計中常在衛星設備上粘貼熱敏電阻作為測溫點,由于衛星的測溫需要通過星務遙測通道采集,星務遙測通道有限,同時考慮到成本、質量等因素,只在衛星重要設備或者結構處粘貼測溫點,因此遙測得到的測溫數據有限,不能得到無測溫點設備的溫度。張旭東等[2]研究通過建立衛星在軌設備溫度的解析解,利用神經網絡預測當前時刻10 s后設備的溫度,但是無法得到當前時刻溫度,并且由于衛星實際存在漏熱等多方面因素,解析解并不能精確估測。劉柏麟等[3]研究了設備溫度與安裝面之間的數學關系,基于傳熱學理論推導出計算設備溫度公式,但是該算法依賴于空間外熱流的變化,估測精度不高。張也弛等[4]研究了基于統計學方法根據幾個遙測點來推斷溫度場,這種方法依賴于遙測點的位置。因此如何通過衛星上已有測溫點的遙測數據去估測無測溫點設備的溫度急需研究。
近年來,機器學習方法在工程中的應用日益增多,在航天中的應用也十分廣泛[5-7]。在本文基于反向傳播(BP)神經網絡優異的非線性系統擬合能力,提出利用BP神經網絡來估測衛星無測溫點設備在軌溫度[8]。
1 BP神經網絡介紹
1.1 BP神經網絡的基本概念
BP神經網絡全稱是反向傳播誤差神經網絡,對于復雜、難以用數學方法準確建模的非線性系統有著優秀的擬合能力[9]。BP神經網絡接受多維數據的輸入,通過輸入層、隱含層、輸出層,輸出數據。輸入數據和輸出數據之間的內在映射關系通過各層神經元之間的連接權值和偏置量來體現。
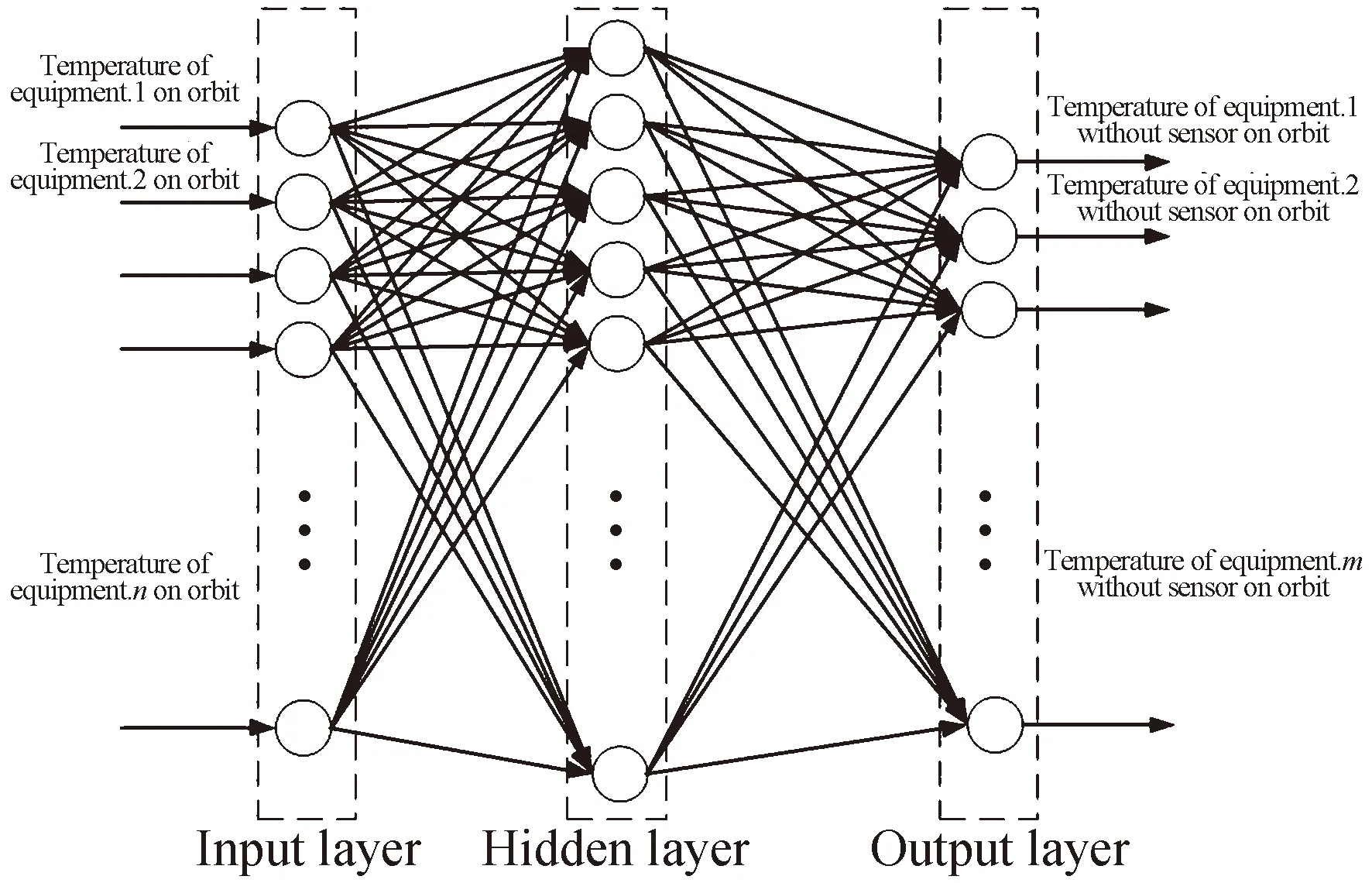
圖1是一個18輸入10輸出的BP神經網絡模型結構。Input為輸入層,Output為輸出層,中間是隱含層(Hidden)。BP神經網絡由輸入層、隱含層和輸出層組成,層與層之間全連接,同一層之間的神經元無連接。輸入值由輸入層輸入,正向流動。修正權值時,網絡根據誤差由后向前逐層修正網絡的連接權值。隨著學習的不斷進行,最終誤差越來越小。

圖1 BP神經網絡結構Fig.1 Structure of BP neural network
BP神經網絡的訓練依賴于大量的樣本訓練,樣本的集合代表性、矛盾樣本多,則所訓練后的神經網絡容易欠擬合。所以訓練時應選擇多樣性、數據量足夠的樣本[10-11]。
1.2 BP神經網絡的應用
BP神經網絡廣泛應用于預測、壓縮、分類等領域,在實際應用中,大約80%的神經網絡模型采取了BP神經網絡模型。熱網絡系統是一個各設備溫度高度耦合的系統,不同設備溫度之間存在互相影響,影響的大小就體現在BP神經網絡模型神經元之間的權值上[10]。使用BP神經網絡擬合衛星熱網絡系統過程就是不斷尋找能夠逼近擬合該衛星設備溫度的BP神經網絡模型神經元的權值和偏置值的過程。BP神經網絡在學習過程中先隨機初始化權值和偏置值,然后通過反向傳播算法調整權值和偏置值,最終達到設定誤差后,獲得最后的權值和偏置值[11]。
2 估測思路
衛星測溫一般通過熱敏電阻(以下稱測溫點)來測溫,星務采集熱敏電阻的信號,轉化成溫度并通過天線傳到地面。熱控分系統設計時一般會在高熱耗設備或者有主動加熱回路設備粘貼熱敏電阻,獲取溫度。一些熱耗較小或者常用的繼承性設備不粘貼熱敏電阻。
∑Dij(Tj-Ti)+qin+qout
(1)
式中:ci為節點i的比熱容;Mi為節點i的質量;Ti為節點i的當前溫度;t為時間;Eij為節點i和節點j之間的角系數;Dij為節點i和節點j之間的接觸傳熱系數;qin為星內熱耗;qout為外熱流[8]。
如式(1)所示,衛星內的溫度場是外熱流與內熱源綜合作用的結果,每個設備與周圍設備和環境通過輻射換熱和導熱進行熱交換,熱交換帶來了溫度的變化。在衛星熱試驗時,為了獲取更多溫度數據和校準熱敏電阻測溫,通常在衛星上粘貼大量的熱電偶。熱電偶成本低,粘貼簡單。熱電偶粘貼的位置根據熱控設計需要,在有熱敏的設備與一些無熱敏的設備上都會粘貼熱電偶,熱試驗后會將所有熱電偶拆除。
熱試驗一般是熱平衡試驗和熱真空試驗[9]。熱試驗中外熱流和內熱源變化形式較多,所得到的溫度數據變化范圍大,具有多樣性。在熱試驗中會得到熱敏電阻的數據和無測溫點上設備熱電偶數據。因此可以通過BP神經網絡,以熱敏電阻溫度數據為輸入,無測溫點設備上的熱電偶溫度數據為輸出,訓練神經網絡,建立起衛星的估測神經網絡。當在軌飛行時,以遙測的熱敏電阻溫度數據為輸入,去估測無測溫點設備的溫度。
3 建立BP神經網絡模型
3.1 樣本數據采集和預處理
在熱試驗中除了熱敏電阻以外,星內粘貼了大量的熱電偶。熱平衡試驗是在星外加載穩態外熱流,星內設備按照工作模式工作。熱真空試驗是通過調節衛星外熱流和設備開關機使得設備溫度達到工作溫度的高低溫極限附近。圖2給出3個設備在熱試驗過程中溫度變化情況。
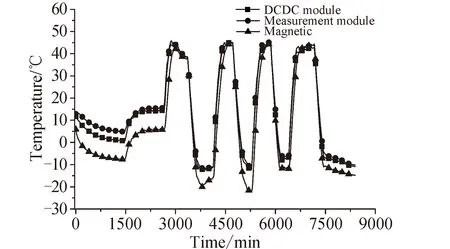
圖2 熱試驗中設備溫度曲線Fig.2 Temperature profiles of equipment of satellite in thermal test
從圖2可以看出衛星在熱試驗期間設備溫度變化范圍比較廣,數據量大,具有廣泛性的特點。
如圖3所示,設備溫度在0~1 470 min為衛星熱試驗低溫工況,設備溫度較低,在1 470~2 660 min為高溫工況,設備溫度上升到較高水平。2 660 min到最后試驗結束,處于高低溫循環過程,設備溫度變化較為劇烈。
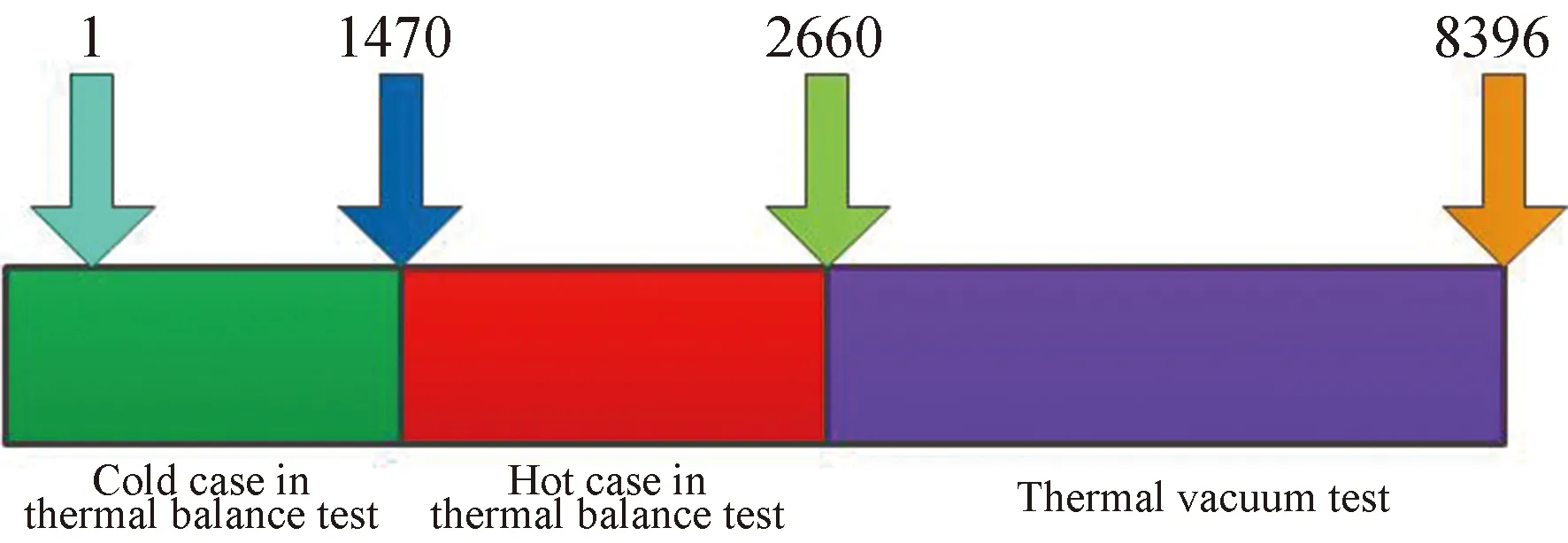
圖3 樣本數據在熱試驗中的分布Fig.3 Samples distribution in thermal test
為了減少各維數據間數量級差別,避免因為輸入/輸出數據數量級差別較大造成網絡估測誤差較大,必須將樣本數據進行歸一化處理。將輸入/輸出值通過歸一化處理映射到[0,1]之間,歸一化采用以下公式:
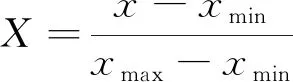
(2)
式中:X為歸一化后的數據;x為原始數據;xmin和xmax為原始數據中的最小值和最大值。
3.2 BP神經網絡建立
BP神經網絡的建立主要包括樣本數據采集、神經網絡訓練等步驟。本文所研究的衛星樣本數據中共有25個星內設備,其中18個設備粘貼有熱敏測溫點,將其作為輸入層,7個設備無熱敏,但是在熱試驗中有熱電偶數據,將其作為輸出層。隱含層的節點數對神經網絡的估測精度影響很大,節點數少會欠擬合,節點數多會過擬合。一般參考如下公式選取(公式之間相互獨立):
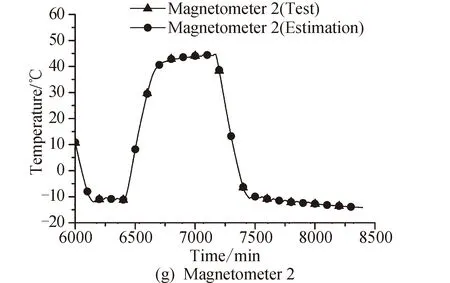
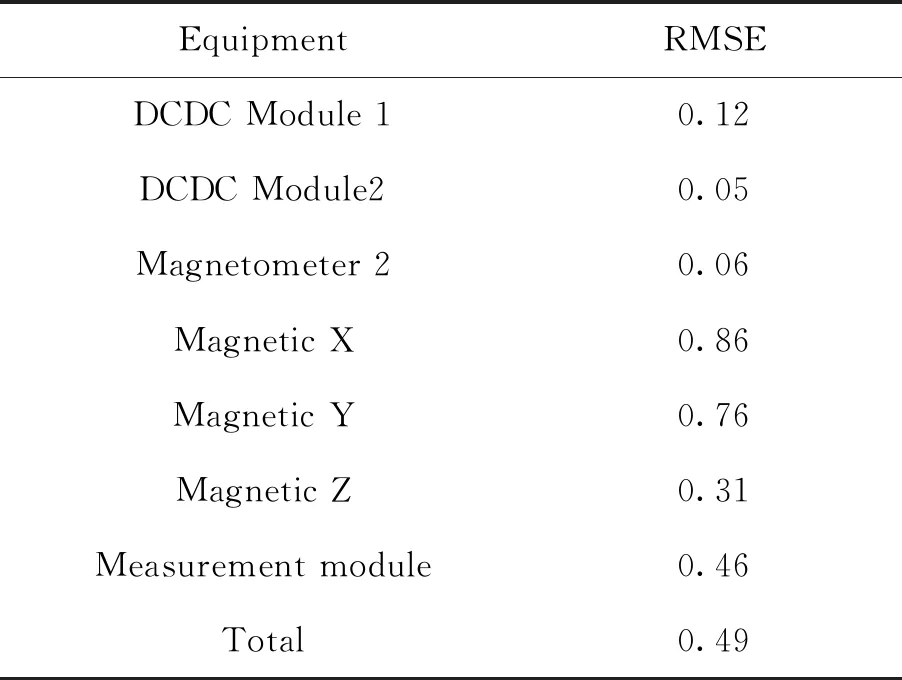
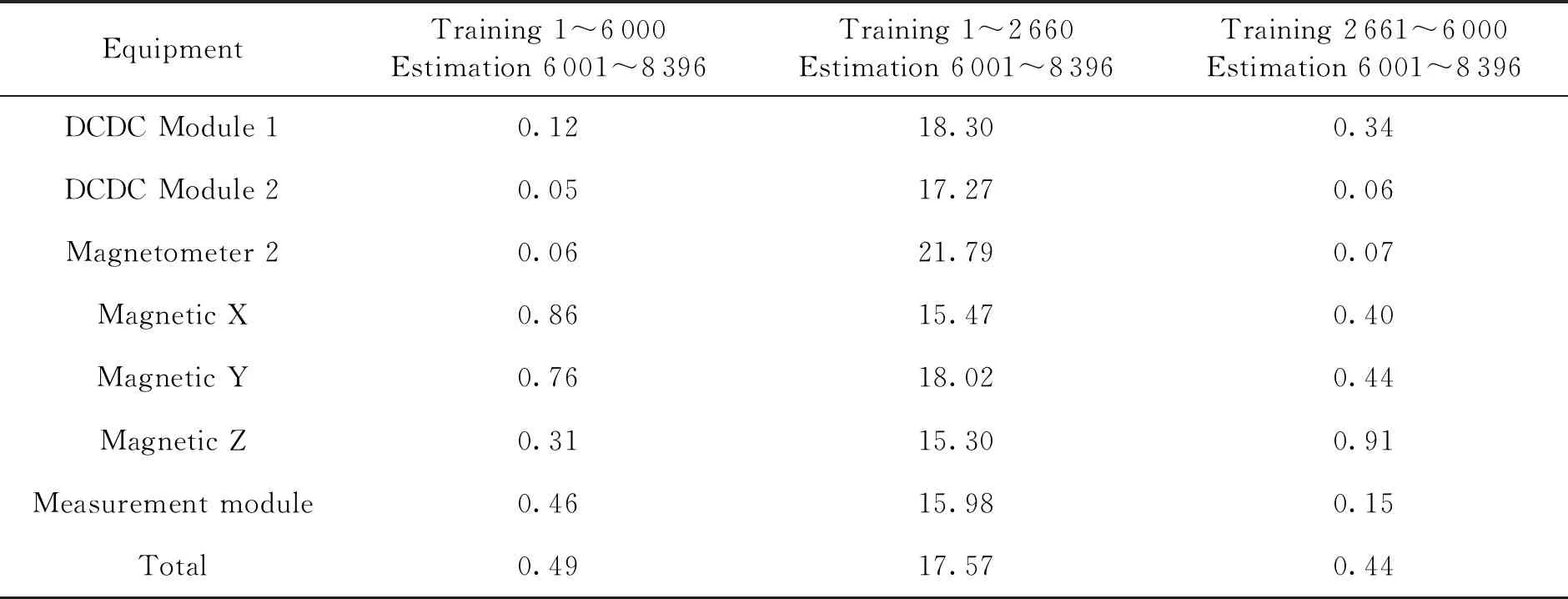
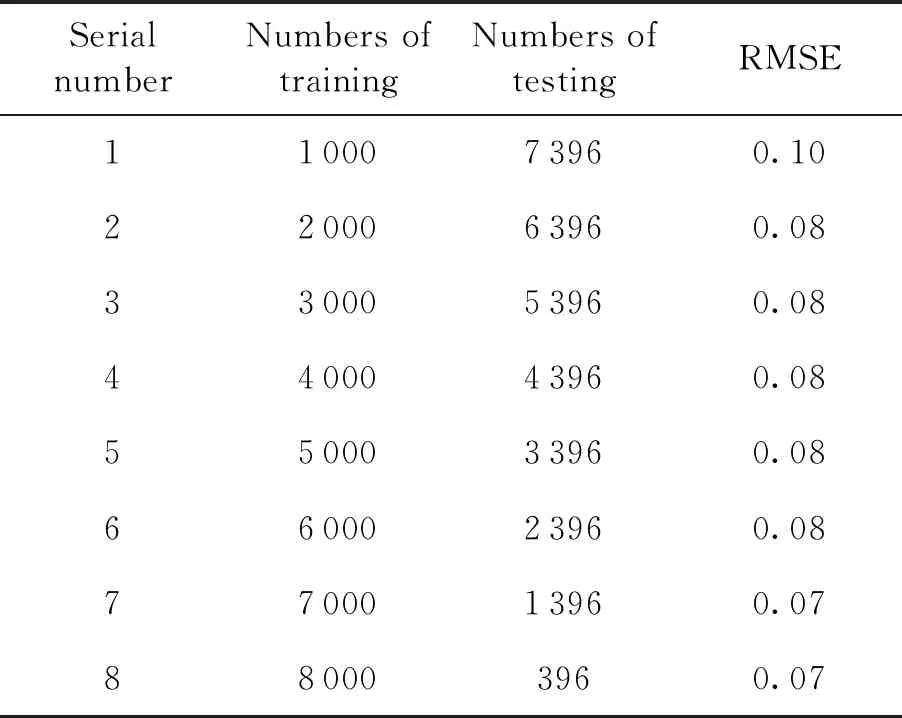
l (3) (4) l=log2n (5) 式中:n為輸入層節點數;l為隱含層節點數;m為輸出層節點數;a為0~10之間的常數。 隱含層節點數的選取并沒有數值解[12],式(3)~(5)也只是參考。本文參考上述公式推薦的數值范圍,并且計算了隱含層節點數6~20之間的神經網絡估測誤差,綜合考慮取隱含層節點數為13。 建立的星上無測溫點設備溫度估測神經網絡如圖4所示。星上設備在軌遙測數據作為輸入層,通過所建立的神經網絡擬合,可得到無測溫點設備的溫度。 圖4 溫度估測神經網絡結構Fig.4 Structure of neural network for temperature prediction 在熱試驗中樣本數據共采集了8 396 min,每分鐘記錄一組28個設備的溫度值,所以共有8 396組有效數據。將樣本數據分為兩部分,一部分為訓練集,一部分為測試集。前6 000 min采集的6 000組數據為訓練集,后2 396 min采集的2 396組數據為測試集數據。用訓練集的數據訓練所建立的神經網絡。 BP神經網絡在初始會隨機生成權值初始值,在后面迭代中根據誤差不斷的更新權值,這樣會造成所建立神經網絡的不可重復性。為了盡可能提高訓練精度,將訓練誤差目標值設為1×10-6,當達到訓練精度,自動保存神經網絡文件。 為了驗證所建立的神經網絡 ,采用所建立的神經網絡估測了熱試驗數據6 001~8 397 min無熱敏的設備的溫度。并把估測值和試驗值進行了對比。 圖5是7個設備的試驗值和神經網絡估測值的曲線。可以看出這7個設備的估測值和試驗值幾乎完全重合。這說明訓練后的神經網絡估測精度很高。 圖5 神經網絡估測值與試驗值對比Fig.5 Comparison between predicted and measured values 續圖5Fig.5 Continued 為評價網絡模型估測結果的精確程度,引入均方根誤差性能函數來評價神經網絡模型[13]。均方根誤差計算公式為: (6) 式中:b為估測數據與真實數據差值;N為測試集數量。 均方根誤差是預測值與真實值偏差的平方與預測次數比值的平方根,常用來作為機器學習模型預測結果衡量的標準。經過計算,對7個設備溫度估測結果的均方根誤差見表1。 從表1中可以看出所有設備估測結果的均方根誤差均小于1,估測精度很高。 表1 估測結果的均方根誤差 本文第3節和第4節中所采取的神經網絡模型訓練數據用的是熱試驗前6 000 min采集的6 000組數據,后2 396 min采集的2 396組數據為測試集數據。而2 660~8 396 min都是熱真空試驗,設備溫度變化相似,都是為高低溫循環。為了研究訓練集對估測結果的影響,進行了不同訓練集對估測結果的影響分析。 分別選取了訓練集為樣本數據中1~2 660組數據,估測樣本數據中6 001~8 396組數據,訓練集為樣本數據中2 661~6 000組數據,估測樣本數據中6 001~8 396組數據,并與第3節和第4節估測的算例進行比較。這3個算例的估測結果均方根誤差見表2。 從表2可以看出,上述3個算例的估測集都為樣本數據中6 001~8 396組數據,而訓練集為1~6 000組數據和2 661~6 000組數據時估測精度接近,當訓練集為1~2 660組數據時,估測精度非常低。分析認為,訓練集樣本的多樣性對估測結果影響很大,BP神經網絡模型的逼近能力與學習樣本的典型性和多樣性密切相關,如果樣本的集合代表性差、矛盾樣本多、存在冗余樣本,網絡就很難達到良好的逼近能力。如果訓練集只是1~2 660組數據(熱平衡試驗數據),無法覆蓋熱真空試驗的數據特征,因此訓練的BP神經網絡模型對6 001~8 396組數據(熱真空試驗數據)估測精度較低。 表2 估測結果的均方根誤差 神經網絡類似于人的學習過程,只有當訓練集足夠多,并且覆蓋多種場景,訓練出的神經網絡模型才能夠估測精度高。 從8 396組數據中隨機抽取若干組數據作為訓練集,以樣本集中除訓練集外的數據為估測集,測試所建立的BP神經網絡模型估測性能。其均方根誤差如表3所示。 表3 訓練集無關性測試結果 從表3可以看出,隨機抽取訓練集訓練出的神經網絡模型估測無測溫點設備溫度的均方誤差仍然很小。并且隨著訓練集數目的增加,均方誤差向減小趨勢發展(由于神經網絡模型初始值的隨機性,估測的均方誤差略有偏差,但是不大)。 值得指出的是,訓練集的多樣性[14]對神經網絡模型的估測精度有著明顯的影響,覆蓋多種場景的訓練集能夠使得神經網絡模型得到更加充分的訓練。為了與表2中訓練集數量進行對比,從樣本數據中隨機抽取了50個數據作為訓練集,用其訓練的神經網絡模型估測溫度的均方誤差為0.498 3,遠遠大于表2中的估測精度,說明了神經網絡模型訓練集選擇的重要性。 本文提出一種使用機器學習方法即BP神經網絡模型來估測星上無測溫點的設備溫度方法。結果表明,利用熱試驗獲得的熱敏電阻和熱電偶的溫度數據訓練的BP神經網絡能夠準確估測無測溫點設備溫度,測試結果顯示估測精度在1℃以內。BP神經網絡模型估測溫度的誤差大小與學習樣本的多樣性和數據量相關。本文利用BP神經網絡估測溫度的方法不僅提供了一種獲取星上更多設備溫度的手段,而且能夠節省測溫資源。后續將根據衛星熱網絡系統特點,以BP神經網絡為基礎,研究復雜網絡模型在估測衛星設備溫度方面的應用。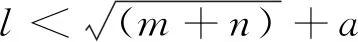
3.3 BP神經網絡訓練
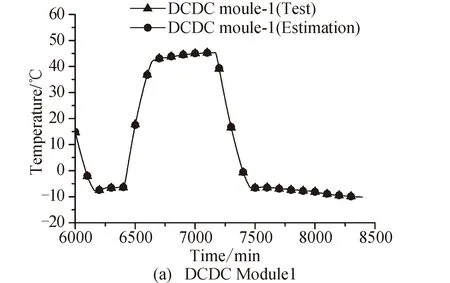
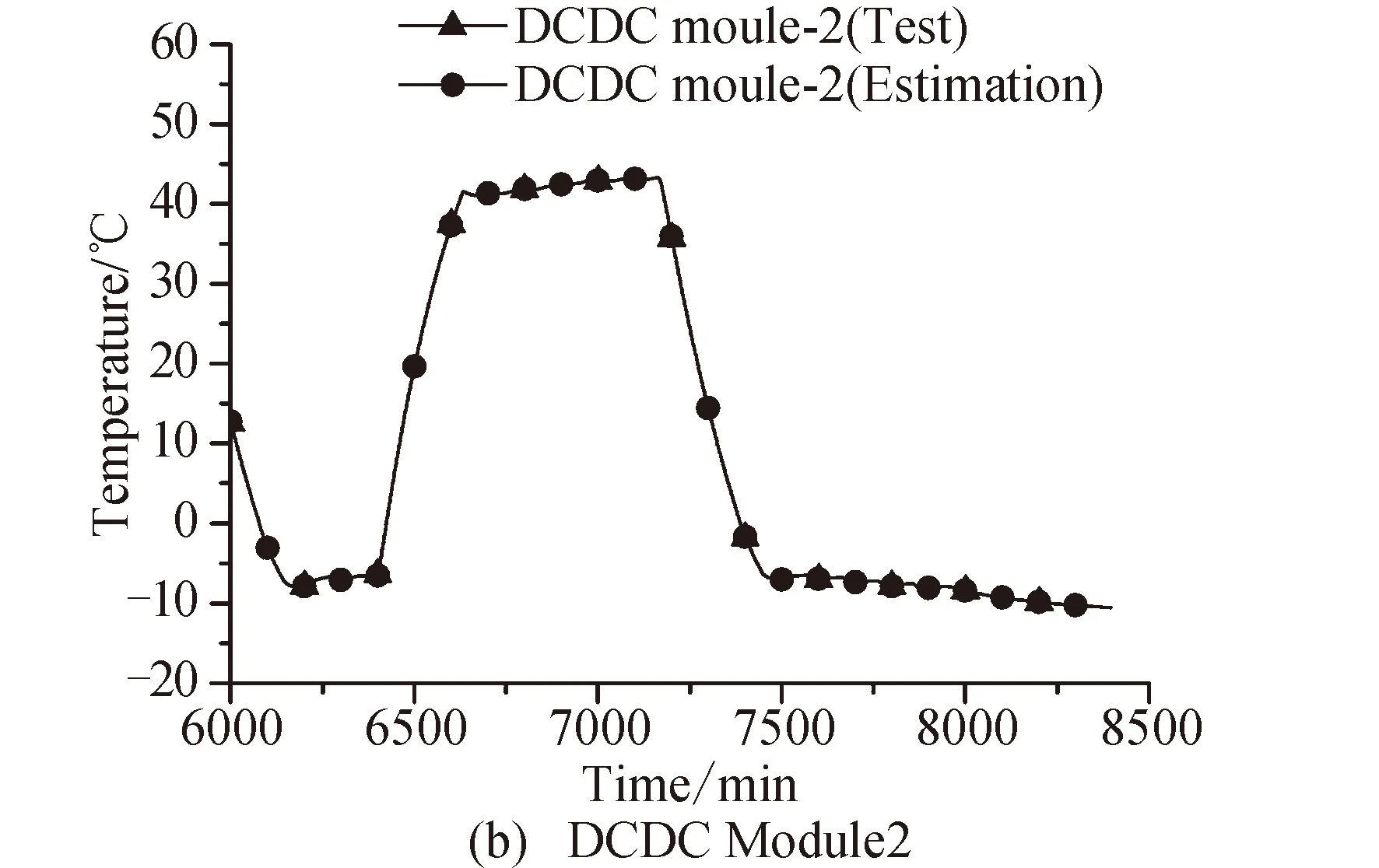
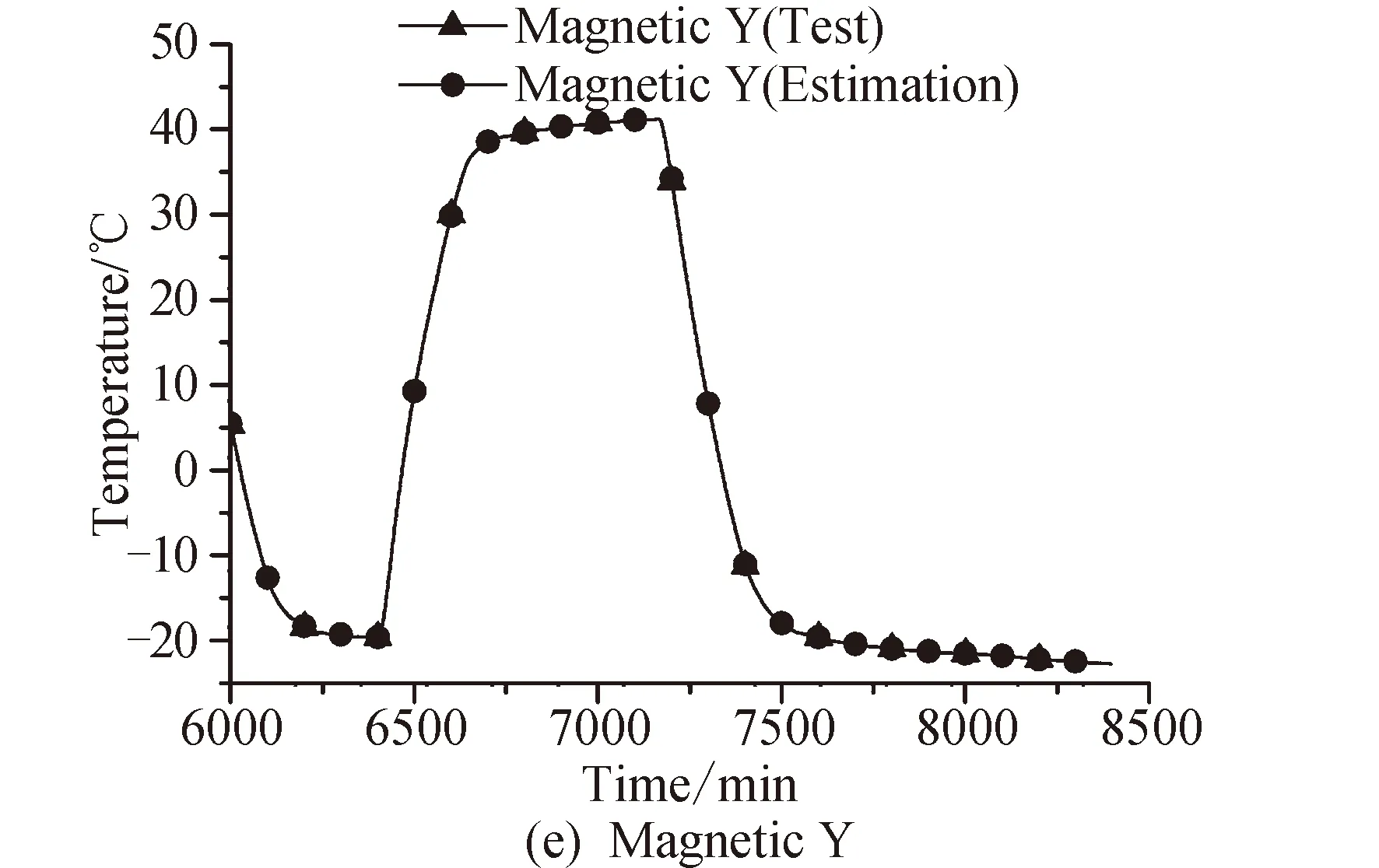
4 溫度估測


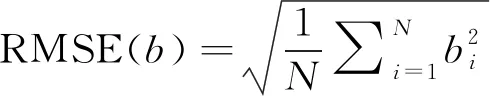
5 訓練集對估測結果的影響分析
6 結束語

