航天器用低溫多層隔熱性能計算方程

張暘，趙劍鋒，韓崇巍，張寧莉，寧博，杜卓林，趙欣，趙啟偉

1. 北京空間飛行器總體設計部, 北京 100094 2. 空間熱控技術北京市重點實驗室, 北京 100094

多層的一維縱向傳熱模型，普遍采用基于導熱和輻射的形式[9-17]。傳熱模型分為兩類,一類為半經驗方程,另一類為逐層建模的方法。半經驗方程以Lockheed[15-16]為代表，多層漏熱量僅與多層內外表面溫度有關，方程中的導熱項系數和輻射項系數由試驗確定。不同的結構、材料，導熱項系數和輻射項系數有較大差異。并且，方程的輻射項為溫度的4.67次方，不便于仿真軟件使用。逐層建模的方法以McIntosh[17]為代表，需建立多層所有相鄰反射屏間的傳熱方程。McIntosh給出了適用于間隔層為滌綸網、蠶絲網、玻璃紙的層間接觸傳熱系數計算公式。此方法受多層結構、材料的限制較小，但是必須求解所有反射屏的溫度，不便于工程應用。

本文將Lockheed和McIntosh的方法相結合，給出了適用于不同組成結構，并且便于工程應用的縱向傳熱模型獲取方法。具體方法為：第一，按照McIntosh的方法逐層建立多層縱向傳熱模型，計算不同熱邊界情況下多層的傳熱量。第二，將多層傳熱模型簡化為類似Lockheed方程的形式，輻射項改為溫度的4次方，以適應仿真軟件。利用第一步得到的計算數據，采用二元線性回歸分析的方法，獲得簡化方程的導熱項系數和輻射項系數。以國產低溫多層為例，研究了常用10單元多層的隔熱性能計算方程。通過等效方法及兩個應用實例，驗證了該方程的準確性。根據研究結果，指出了純輻射模型以及純導熱模型的問題根源。

最后，研究了如何選取多層熱平衡試驗工況的問題。其難點是如何通過有限的試驗工況獲得足夠的回歸分析數據，即如何選擇典型試驗工況。經分析，確定了7個典型的試驗工況，并給出了試驗裝置的選擇建議。

本文的研究成果可以直接用于國產航天器低溫多層的熱設計、熱仿真。考慮到低溫多層的相似結構，本文提出的研究方法可用于其他類型低溫多層。

1 一維縱向傳熱模型

1.1 熱數學模型

航天器用低溫多層包括兩部分：多層芯和面膜。多層芯由反射屏和間隔層組成。反射屏為6 μm厚的雙面鍍鋁聚酯打孔膜，間隔層為滌綸網。1層反射屏和1層滌綸網組成一個隔熱單元。常用的隔熱單元數為5單元、10單元、20單元。為便于多層制作，常增加1個反射屏，使多層芯的內外表面均為反射屏。面膜有兩種：一種是黃膜，為25 μm厚帶ITO膜的單面鍍鋁聚酰亞胺薄膜；另一種是黑膜，為25 μm厚黑色滲碳聚酰亞胺膜。圖1為多層組成結構示意。

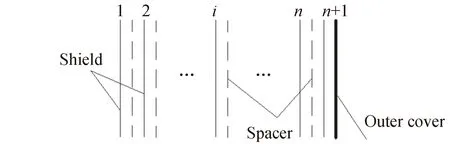
圖1 多層結構組成Fig.1 Assembly structure of MLI

將多層縱向傳熱模型簡化為僅有輻射和導熱，忽略比重較小的層間分子導熱(高真空)。按照圖1可建立n單元多層相鄰反射屏間的n個傳熱方程：

(1)

式中：i=1～n為反射屏編號；Ti為第i個反射屏的溫度(K)；εi,i+1為反射屏間的等效發射率；σ為波爾茲曼常數；ki,i+1為層間接觸傳熱系數(W·m-2·K-1)；q為多層傳熱量(W/m2)。面膜和第n+1層反射屏之間無間隔層，可認為二者是等溫的。

反射屏間的等效發射率εi,i+1為：

εi,i+1=1/(1/εi+1/εi+1-1)

(2)

文獻[17]給出了反射屏發射率εi隨溫度變化的計算式，考慮了反射屏打孔的影響：

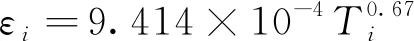
(3)

根據文獻[15]可得間隔材料為滌綸網時層間接觸傳熱系數ki,i+1的計算公式：

ki,i+1=0.008×f×k/ΔX

(4)

式中：f為滌綸網的相對密度(滌綸網面密度÷網厚度÷滌綸的體密度); ΔX為滌綸網的厚度。NASA某運載上面級低溫儲罐用多層[18]使用的滌綸網相對密度f=0.03。實測國產滌綸網面密度為10.615 g/m2，滌綸網厚115 μm，查材料手冊滌綸的密度為1.39×106kg/m3。得國產滌綸網相對密度f=0.0664。k為滌綸材料的導熱率，

k=0.017+7×10-6(800-Tm)+0.022 8ln(Tm)

(5)

式中：Tm為相鄰反射屏的算術平均溫度。

按式(1)可得n個方程，未知數為q，T1～Tn+1共n+2個，對任意給定的(T1、Tn+1)組合方程組均可解。

1.2 隔熱性能計算方程

為了便于工程應用，期望隔熱性能計算方程具有以下特性：第一，形式為導熱項加輻射項(溫度的4次方)；第二，變量僅包括傳熱量、多層冷/熱面的溫度；第三，等效導熱項系數keff、等效輻射項系數εeff均為常數。

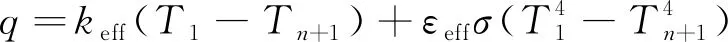
(6)

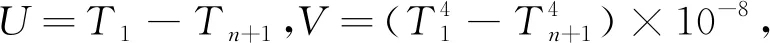
二元線性回歸方程q=f(U,V)描述的是空間的一個平面，平面區域的輪廓由自變量U、V的取值范圍確定。樣本到平面的距離，代表回歸方程的偏差，偏差越小回歸方程的效果就越好。

線性回歸的效果與樣本密切相關[18-19]，一般要求樣本容量大于30，并且在求解區域內均布。應用于低溫多層的情況：首先，確定U、V的取值范圍、確定求解區域；其次，在求解區域內均布樣本。U、V的取值范圍需要由T1、Tn+1轉換。根據低溫多層的耐溫能力及應用經驗，可以確定冷熱面溫度范圍。T1為多層熱面溫度，取值范圍為150～390 K(-123～117 ℃)；Tn+1為多層冷面溫度，取值范圍為90～390 K(-183～117 ℃)，由T1、Tn+1組成的求解區域如圖2(a)所示。圖2(a)中，ΔABE的區域與梯形ABCD內的區域關于直線AB對稱，因此僅需考慮梯形ABCD區域。梯形ABCD區域映射為圖2(b)所示的紡錘形區域B′C′D′A′(B′)。在圖2(b)中均布35個樣本，不含坐標原點。35個樣本在原坐標系下的分布如圖2(a)所示。

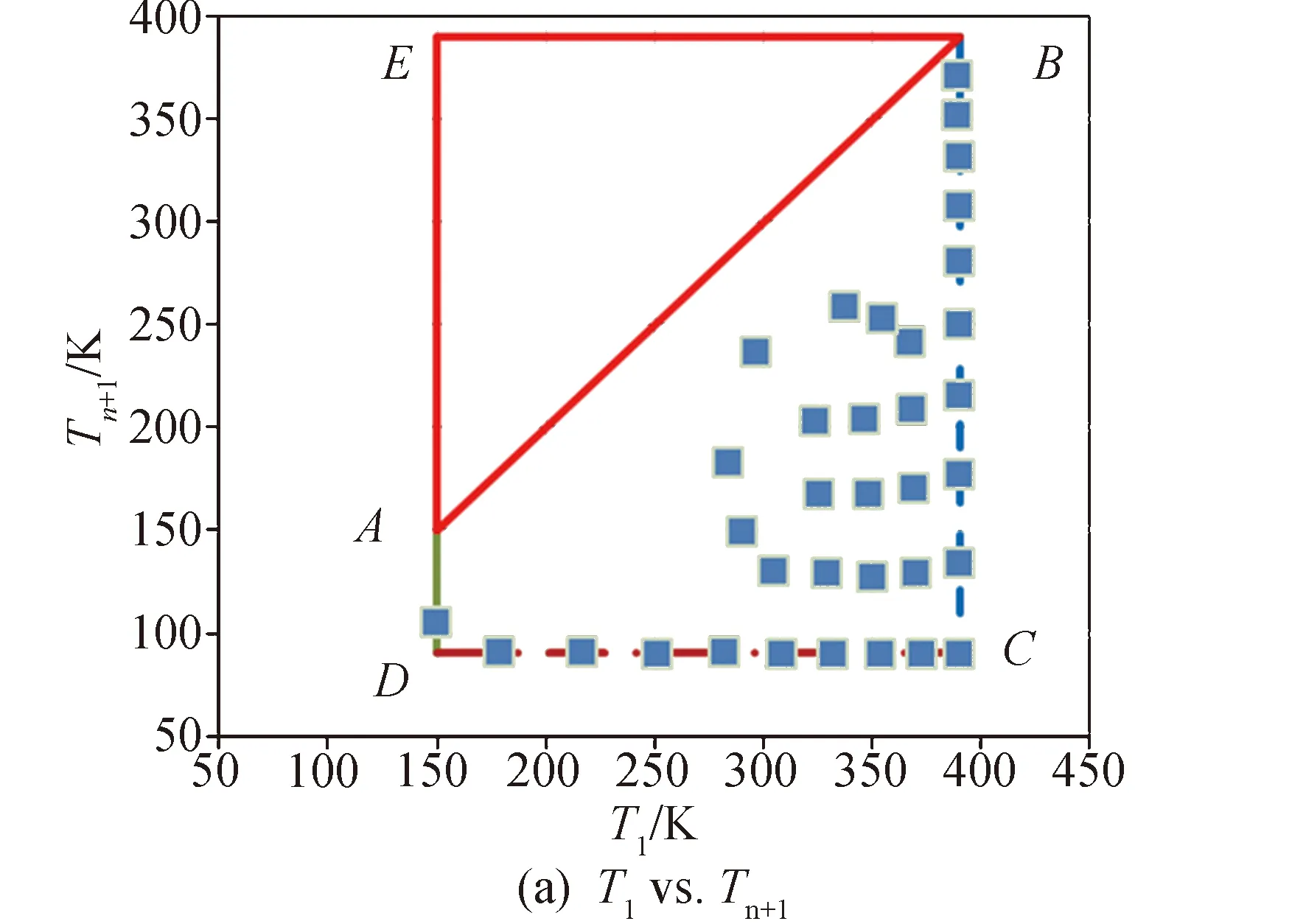
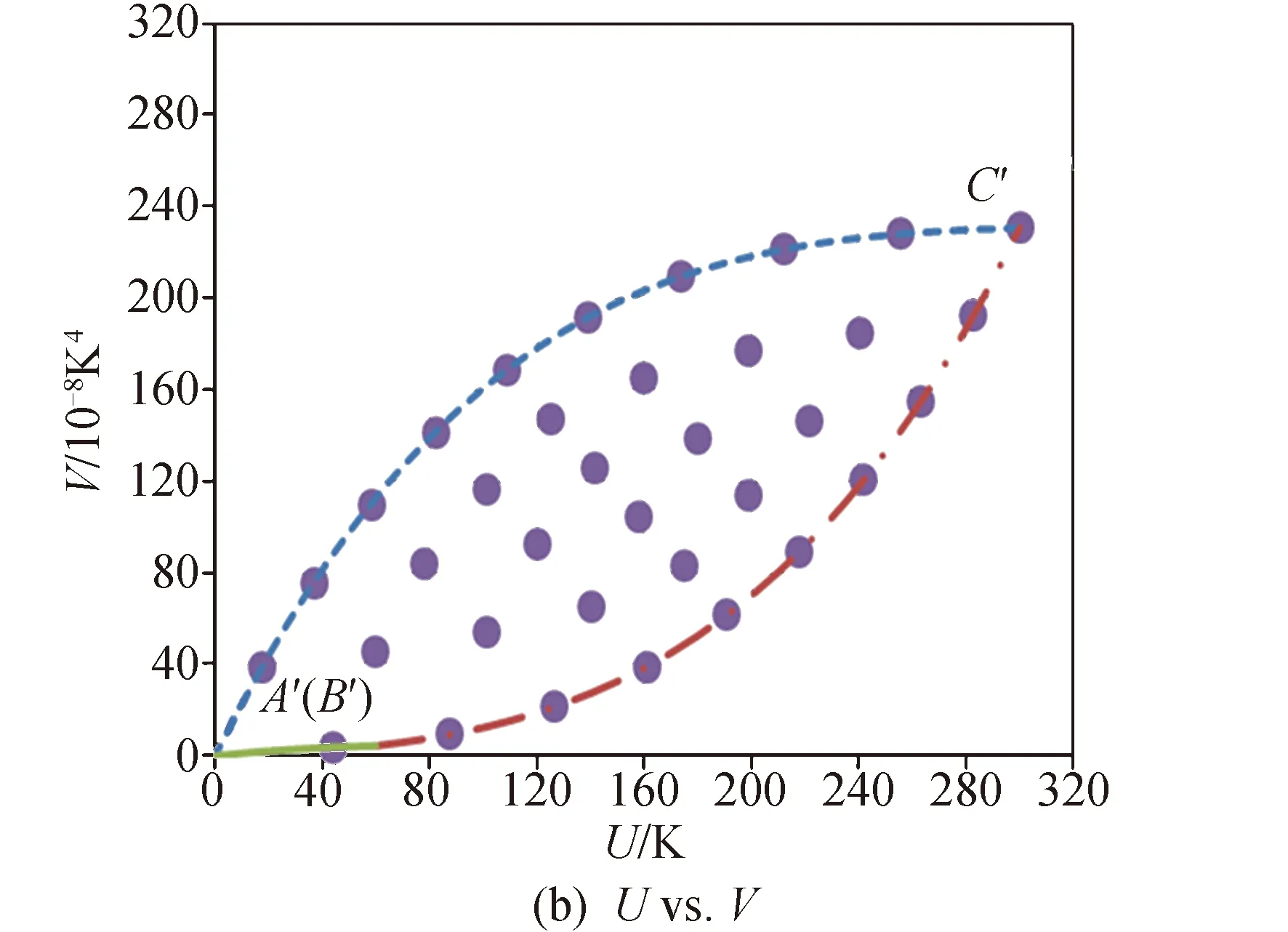
圖2 求解區域及樣本分布Fig. 2 Solution region and sample distribution

線性回歸的效果還需通過回歸方程的顯著性檢驗及回歸系數的顯著性檢驗[18-19]。檢驗項目以及判據見表1。R2檢驗用于衡量回歸方程的優劣性，即擬合程度如何。F檢驗用于檢驗因變量與自變量是否存在顯著的線性相關關系。t檢驗用于檢驗每個自變量的系數是否顯著為零，即方程中是否有多余的自變量。表中，k為自變量個數，n為樣本容量。

表1 顯著性檢驗項目

綜上所述，獲得隔熱性能計算方程一般分4步。第一，確定樣本的自變量取值。根據圖2確定(T1、Tn+1)的35種組合。第二，獲得樣本的因變量值。對每一對自變量，求解按第1.1小節建立的方程組，獲得35個因變量值(q)，從而獲得35個觀測樣本(q，T1，Tn+1)。第三，利用觀測樣本，按式(6)進行線性回歸，獲得常數項系數。第四，按表1進行顯著性檢驗。

2 算例

以10單元低溫多層為例。按第1.2小節的方法獲得了兩組觀測樣本，分別對應f=0.064、f=0.03，如表2所示。從表2可知，f值對多層的漏熱量q影響較大，國產多層應采用相對密度更小的滌綸網以提高隔熱性能。將兩組樣本繪制成三維散點圖，并將散點擬合成三維曲面，如圖3所示。可見散點擬合的曲面均為平面，直觀判斷式(6)的形式是正確的。

利用專業軟件做回歸分析，回歸方程的形式為：

q=b0+b1U+b2V

(7)

得b0=-0.007 8，b1=0.061 4，b2=0.02/5.67。b0很小，對漏熱量影響可忽略，令b0=0。對照式(6)，得keff=0.061 4，εeff=0.02/5.67。最終，將隔熱性能計算方程寫為：

(8)

顯著性檢驗結果為：R2=0.999 9接近于1；F檢驗為1.75×105>F0.05(2,32)=5.34。回歸系數的顯著性檢驗結果為：b1的t值為482.4，b2的t值為135.3，均大于t0.05(32)=2.04。可見，回歸方程的效果是很好的。此外，按式(8)計算的漏熱量與樣本q值最大偏差為2.4%，平均偏差為0.8%，方程的精度較高。

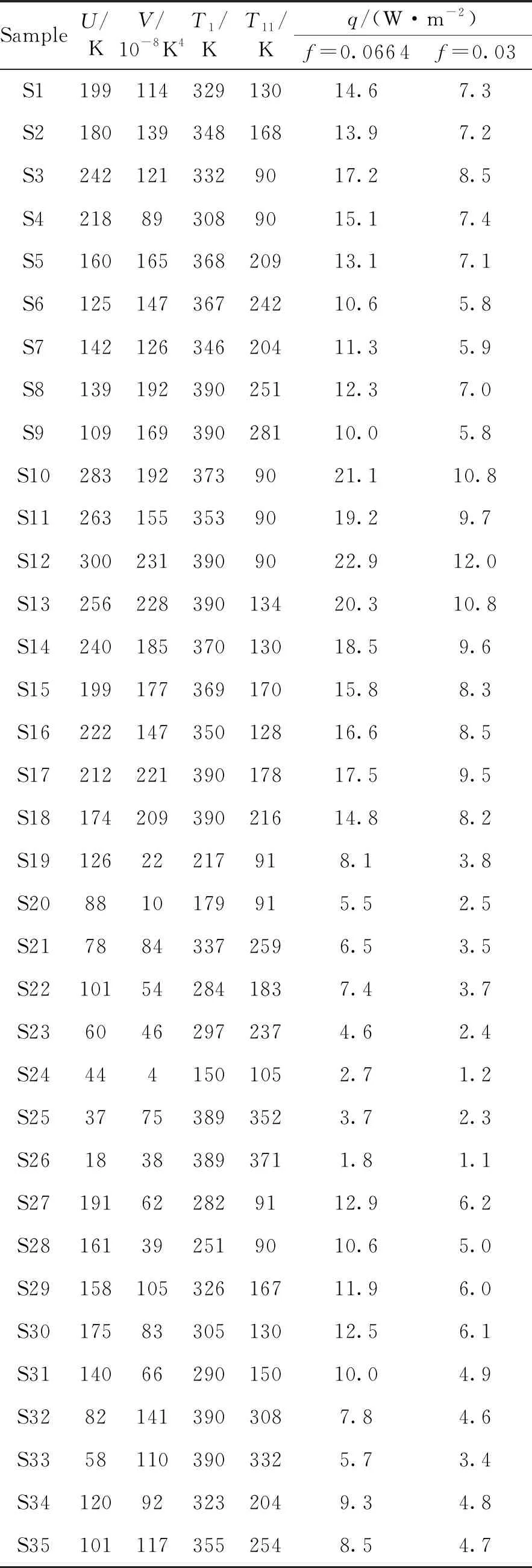
表2 10單元多層樣本

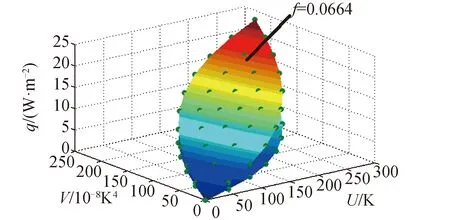
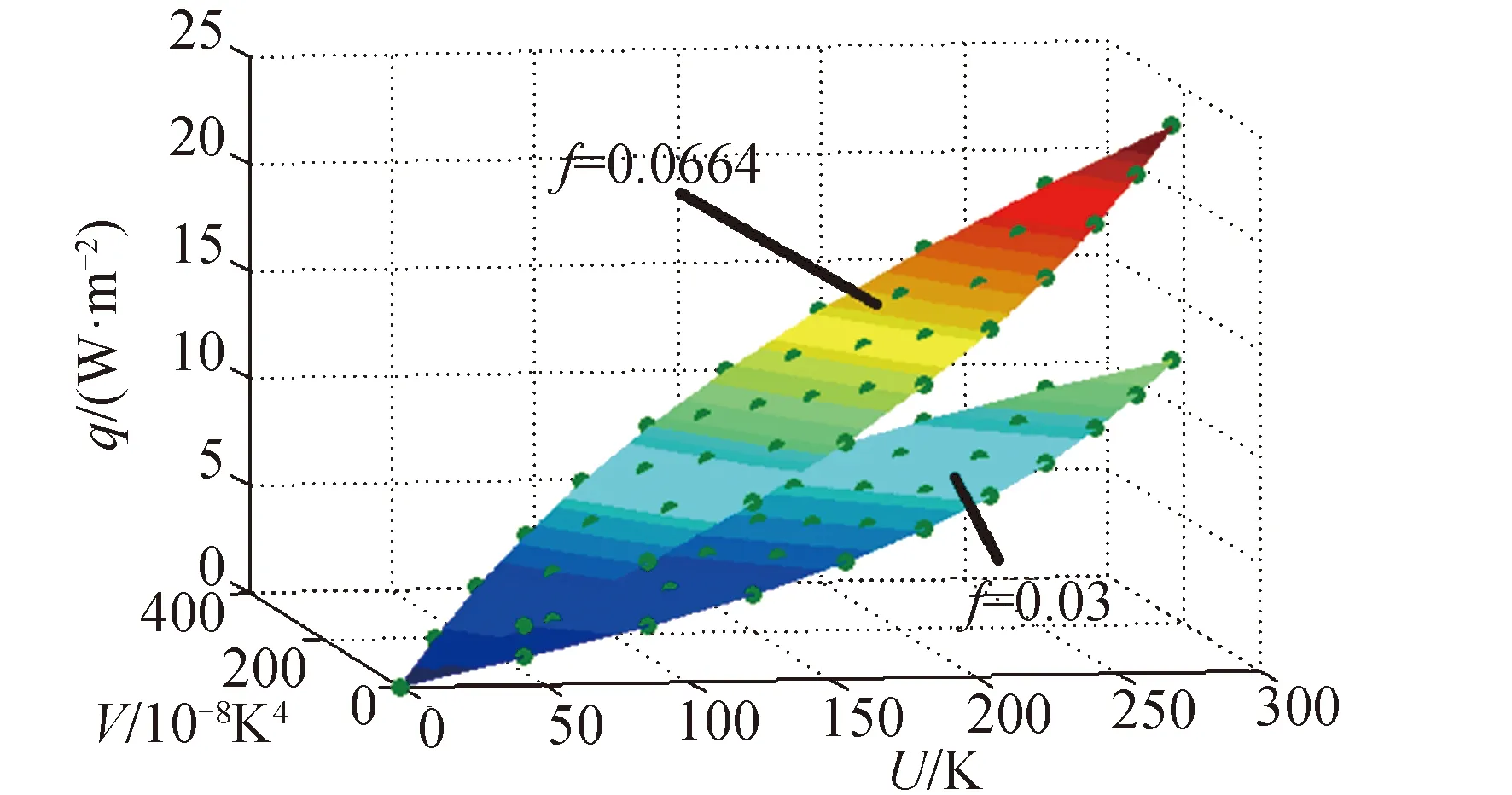
圖3 樣本三維曲面Fig. 3 Sample 3D surface

3 驗證計算方程

3.1 常用溫度條件等效驗證

為了避免有限次試驗數據帶來的誤差，并且省去大量、繁雜的試驗數據處理工作。先采用等效的驗證方法，驗證常用溫度條件。再進行典型低溫、高溫工況的驗證。

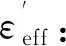
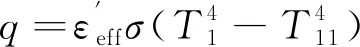
(9)

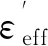
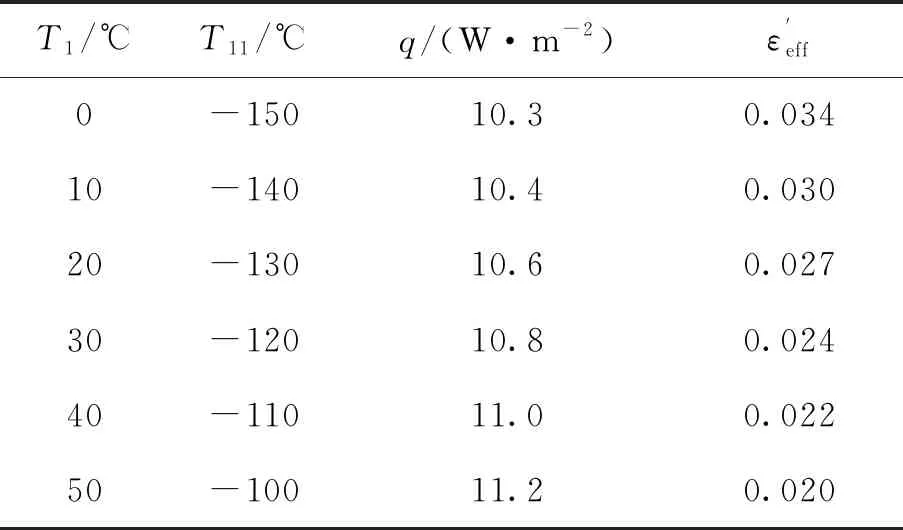
表3 10單元多層等效驗證

3.2 典型高溫、低溫工況驗證

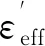
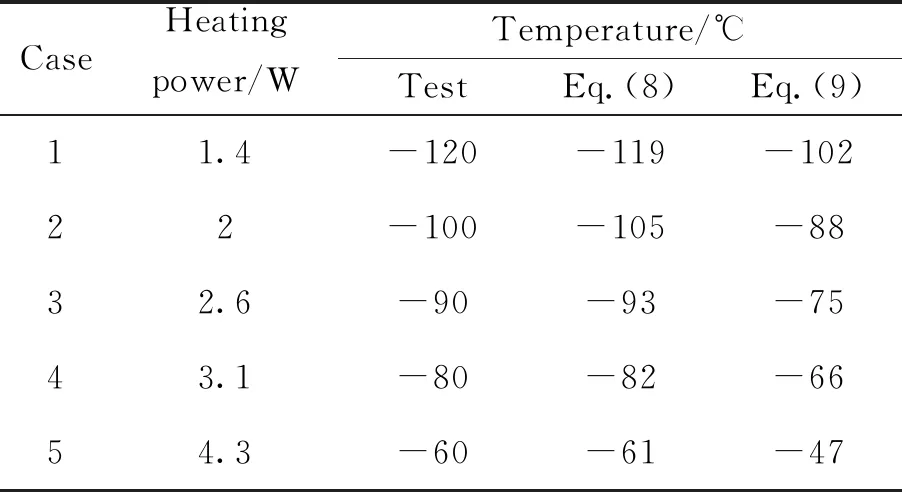
表4 地面試驗仿真結果

圖4 在軌仿真結果Fig. 4 Inorbit simulation result

4 有效發射率取經驗值的問題根源

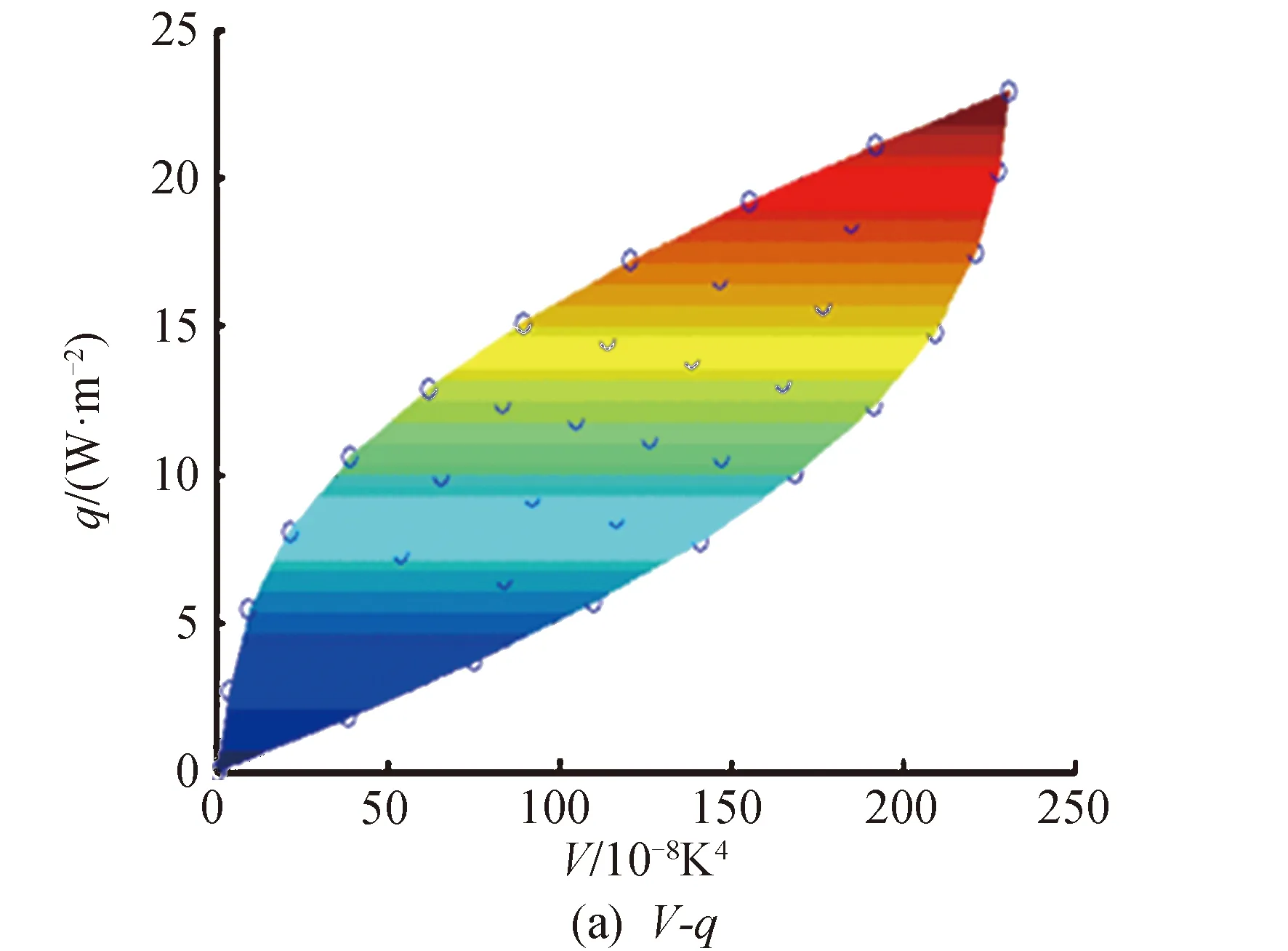
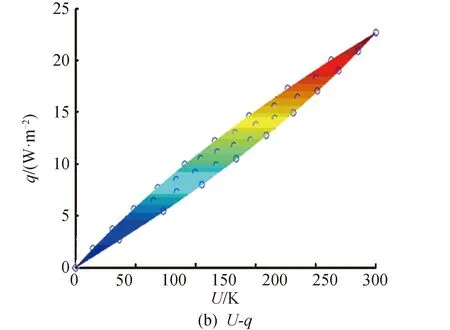
圖5 平面投影Fig. 5 Plane projection

5 試驗工況設計

本文只研究試驗工況設計相關的問題，包括兩方面：如何選取試驗樣本，即試驗工況如何確定；以及如何實現試驗工況，即采用什么試驗裝置完成試驗。

多層熱平衡試驗時間很長，真空罐、液氮等試驗費用昂貴。若按第1.2小節取35個樣本，很難實現，因此需要研究最小樣本容量。按文獻[20]，可得樣本容量的下限要求。第一，欲使回歸參數存在，樣本容量(n)至少比模型自變量個數(k)多1，即n≥k+1；第二，t檢驗對樣本最小容量要求為n>k+5；第三，為了提高估計精度，要求n>2k。因此，對二元線性回歸，樣本容量至少為7個，不含坐標原點。按照樣本均布的原則，布置7個樣本，如圖6中S1～S7。樣本的坐標及其對應的多層冷熱面溫度見表5。

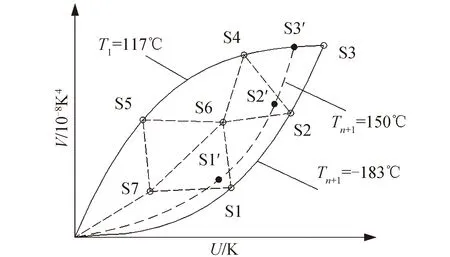
圖6 試驗樣本分布Fig. 6 Thermal balance test sample distribution

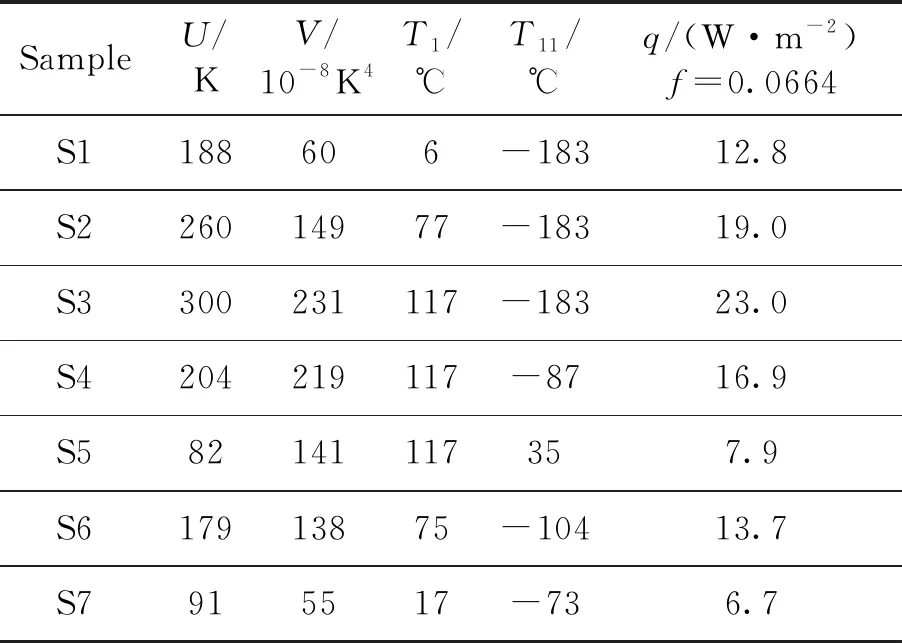
表5 熱平衡試驗樣本

要實現表5的試驗樣本，多層冷、熱面都必須控溫。多層熱面控溫比較容易實現，控制熱面加熱器功率即可。多層冷面溫度控制要復雜得多，與試驗裝置有關。根據冷面不同的控溫原理，將試驗裝置分為三類[6,10]。第一類為汽化型，第二類為對流換熱型，第三類為輻射換熱型。

汽化型裝置：多層的冷面緊貼一個容器，容器內填充低溫工質(液氮、液氦等)，靠液態工質汽化維持冷面溫度恒定，并根據汽化量計算多層漏熱。這種試驗裝置精度高，一般用于多層冷面溫度較低情況的性能測試。缺點是試驗系統復雜,費用昂貴。

對流換熱型裝置也需要一個容器存放低溫工質，但工質不汽化，靠工質與容器壁面對流換熱控制冷面溫度。這類設備適用于冷面溫度不是很低的情況。測量精度不如汽化型，但冷面溫度可連續控制，裝置簡單，費用不高。

輻射換熱型裝置更簡單，僅需將試驗件吊掛在真空罐內，多層冷面與真空罐壁直接輻射換熱。根據經驗，此方法所得的多層冷面溫度受多層熱面溫度影響很小，冷面溫度一般為-150℃左右，該方法對冷面的主動控溫效果較差。

綜上所述，針對表5的S1～S3樣本，可采用汽化型裝置，選液氮為汽化工質。為了節約試驗經費也可以采用輻射換熱型裝置。此時冷面溫度為-150℃左右，對應的樣本變為S1′S2′S3′，稍偏離原樣本。其余樣本需采用對流換熱型裝置，實現多層冷面溫度的主動控溫。

6 結束語

本文以間隔層為滌綸網的國產10單元低溫多層為例，研究了獲取低溫多層隔熱性能方程的方法。此方法具有普遍適用性，可用于任何單元數、間隔層為玻璃紙或蠶絲網的情況。

與低溫領域常用的Lockheed方法相比，本文給出的隔熱性能計算方程可更方便地用于熱仿真軟件，并且有足夠的計算精度。

本文描述的隔熱性能計算方程針對一維縱向傳熱過程，適用于大面積應用的多層。若多層面積較小，還需考慮多層的橫向漏熱問題。