基于UDKF的非共面陀螺在軌自主標定方法

張曉文，李驥

1. 北京控制工程研究所，北京 100190 2. 空間智能控制技術國家級重點實驗室，北京 100190

陀螺是航天器重要的姿態測量敏感器，存在安裝誤差、常值漂移和刻度因子誤差等影響角速度測量精度的參數。這些陀螺參數雖然可以在地面精度標定，但是在航天器入軌之后還會發生變化。因此對于定姿精度要求高的任務，或是需要陀螺獨立外推一段時間姿態的任務，有必要對陀螺參數進行在軌標定。常規航天器使用基于星敏和陀螺測量的6階濾波器同時估計本體姿態和陀螺常值漂移，忽略陀螺安裝誤差和刻度因子誤差。

在NASA的卡西尼探測器上，設計有15階卡爾曼濾波，對3部正交安裝陀螺的常值漂移、安裝誤差和刻度因子共12個參數進行在軌標定[1-3]。每次標定分別繞本體系三軸旋轉±180°，共持續4-5小時。從2002年到2016年，每年至少進行一次標定，其結果顯示，安裝誤差和刻度因子在被標定更新之后保持了良好的穩定性。在2013年，嫦娥三號著陸器成功飛行應用了一種以星敏測量的姿態四元數和陀螺測量的角度增量作為輸入，結合姿態機動，利用UD分解卡爾曼濾波(UDKF)在軌標定陀螺組件的常值漂移、安裝誤差和刻度因子誤差的方法[4]。以上兩例標定方法的不足之處是要求陀螺組件標稱為正交安裝，因此限制了其使用范圍。出于冗余備份考慮，很多陀螺組件采用3部正交安裝陀螺加1部傾斜安裝陀螺的構型。在2014年，月地高速再入返回器成功飛行應用了一種基于最小二乘的可對非正交安裝陀螺參數在軌標定的方法，通過一段時間的統計得到陀螺等效漂移的均值，實現計算的輕量化[5]。該方法的使用前提條件是星體角速度控制穩定度較高，因此適于用動量輪或控制力矩陀螺控制姿態的航天器，而不適于用噴氣控制姿態的航天器。2016-2017年，在NASA的GOES-16衛星上測試驗證了一種通過類似正弦抖動激勵和傅里葉分析在軌標定陀螺刻度因子的方法[6]。該方法優點是不需要航天器做大角度機動，因此標定期間星上載荷可以正常工作，缺點是未標定陀螺安裝。Zhang[7]研究了非正交安裝陀螺常值漂移和刻度因子的在軌標定方法，但是未考慮陀螺安裝誤差。

有些航天器配置有由陀螺和加速度計組成的慣性測量單元。彭惠[8]、王易南[9]、Lu[10]等以星敏和衛星導航接收機作為測量信息來源，將慣性測量單元中陀螺和加速度計的安裝誤差和刻度因子等參數共同作為狀態變量在一個濾波器中進行估計。

現有研究表明，為了保證陀螺在軌標定算法系統可觀，需要航天器進行姿態機動。給定姿態機動序列或軌跡，利用奇異值分解[11]、李導數[12]或是分段線性定常系統可觀性理論[13][14]等方法可以分析系統可觀性，但是分析計算過程不夠簡潔。

為解決非正交安裝陀螺組件在軌標定問題，對現有的正交安裝陀螺組件在軌標定方法[4]進行改進和完善，提出一種基于UDKF的非共面安裝陀螺組件在軌自主標定方法。首先，建立非共面陀螺定姿誤差模型，并以此建立狀態方程；然后，通過正交變換建立測量噪聲解耦的測量方程；接著，給出從狀態變量求解安裝誤差和刻度因子誤差的精確公式；然后，通過公式推導證明原方法[4]是本方法在陀螺組件為正交安裝條件下的特例；之后，基于可觀性分析給出簡潔的系統可觀的角速度組合條件；最后通過數學仿真驗證本方法的有效性。

1 陀螺參數標定算法

1.1 非共面陀螺定姿誤差模型

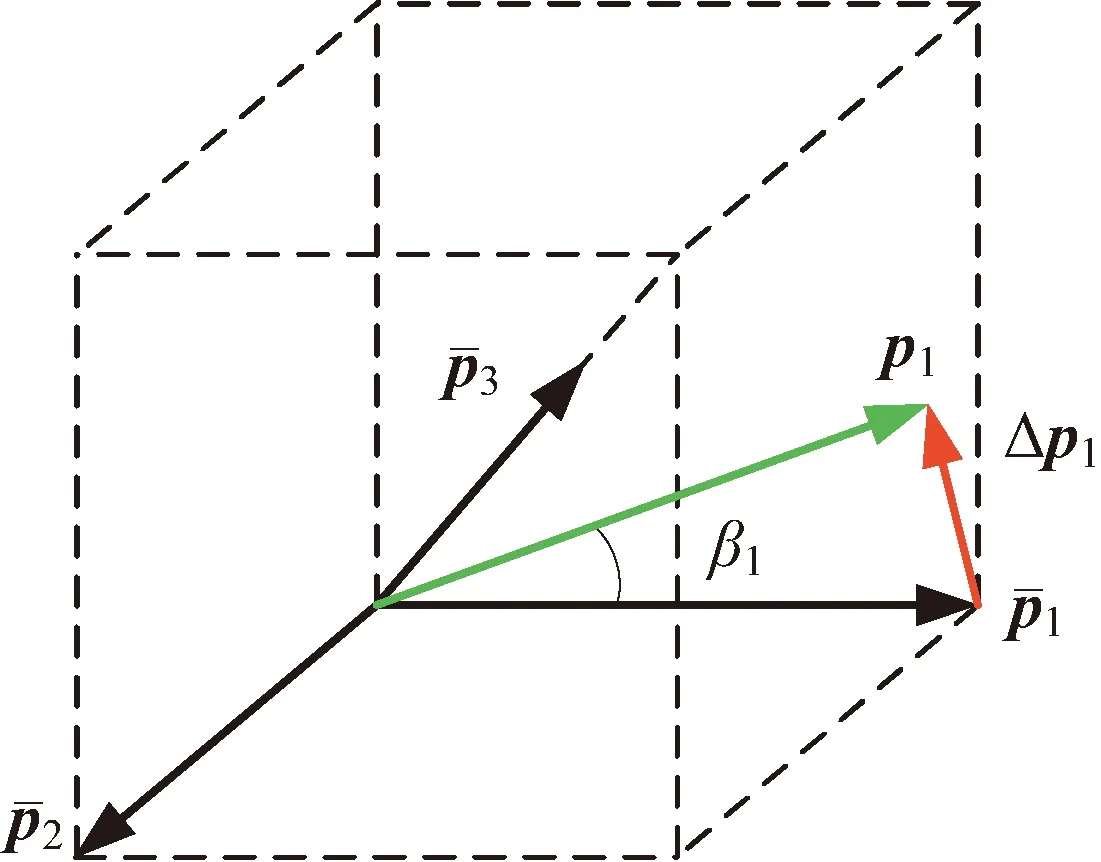
圖1 陀螺安裝誤差示意Fig.1 Gyro misalignment diagram

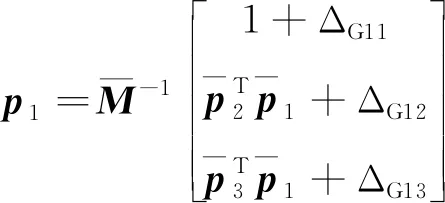
(1)

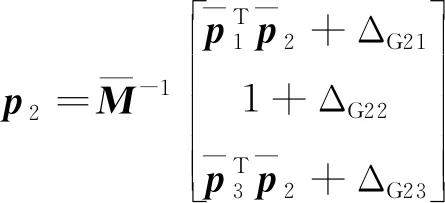
(2)

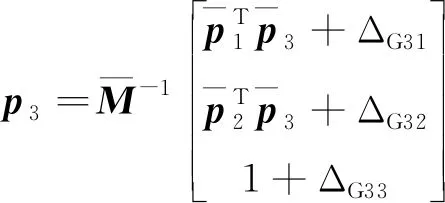
(3)

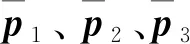
記3個陀螺的刻度因子誤差為ΔKGi，常值漂移為bG，測量噪聲為nG，則陀螺組件測量的本體角速度的誤差為：

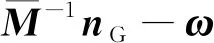
(4)

式中：ω為真實的本體角速度矢量。

定義如下輔助變量：

(5)

則式(4)變為：

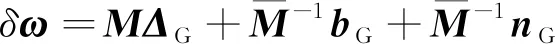
(6)

由式(5)得：

可知，輔助變量ΔG中各元素是陀螺刻度因子誤差和安裝誤差的非線性組合。

在小角度假設下，陀螺定姿誤差θ的傳播方程為[15]：

(8)

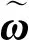
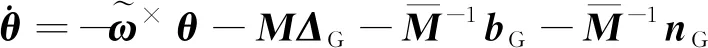
(9)

1.2 濾波器設計

為了提高標定算法的精度，濾波器實際估計的是陀螺常值漂移經過常規方法估計后的殘差。這里為了簡化表達仍然采用bG來表示。陀螺常值漂移不穩定性建模為：

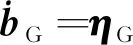
(10)

式中：ηG為隨機白噪聲。

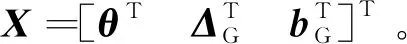
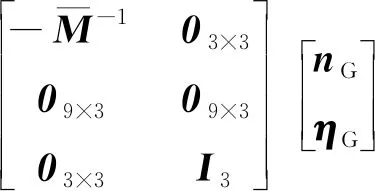
(11)

將星敏測量的本體姿態與陀螺外推的姿態相比較，可得到陀螺定姿誤差的測量值，其與真值滿足如下關系：

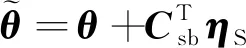
(12)

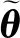
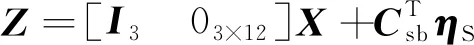
(13)

為保證標定算法的穩定性，濾波器具體實現采用UDKF[16]。UDKF為了序貫處理測量更新，要求測量噪聲方差陣為對角陣。為此，將式(13)兩邊左乘正交陣Csb，得到測量噪聲方差陣為對角陣的新的測量方程：

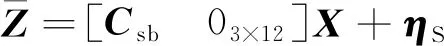
(14)

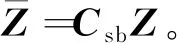
由狀態變量定義知，濾波器是直接估計陀螺常值漂移，間接估計陀螺刻度因子誤差和安裝誤差。這里采用間接估計的好處是狀態方程為線性。

1.3 UDKF算法

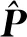
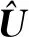
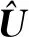
式中:

j=n,n-1,…,2

i=1,2,…,j-1

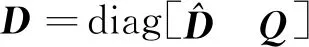
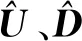
初始化:

α1=r+v1f1

對于j=2,3,…,n,

αj=αj-1+vjfj

最后濾波增益為:

得到濾波增益K后，采用與常規卡爾曼濾波相同公式求取狀態變量估計。

1.4 安裝誤差和刻度因子誤差求解

由于濾波器給出的是陀螺安裝誤差和刻度因子誤差的間接估計，即輔助變量ΔG的估計，因此還需要進一步求解。式(5)包含9個方程，而待求解的陀螺參數共有12個，因此不能得出唯一解。如果要得出唯一解，需要增加約束條件。由式(5)得

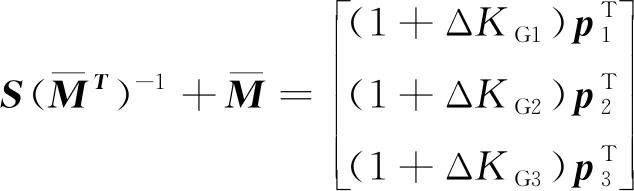
(15)

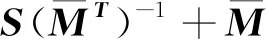
ΔKGi=‖ei‖-1

(16)

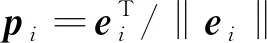
(17)

則陀螺安裝誤差矢量為：

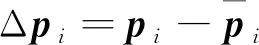
(18)

1.5 正交安裝特例

在工程應用中，地面精確標定后的陀螺安裝誤差角一般不會超過0.1°。以陀螺1為例，當其安裝誤差角β1取0.1°時，安裝誤差分量ΔG11約等于1.523×10-6。可見，ΔG11的數值非常小，因此可以忽略。同理ΔG22和ΔG33也可以忽略。此外，再忽略ΔKG1ΔG12等二階小量，則由式(7)可得陀螺安裝誤差和刻度因子誤差的近似計算公式：

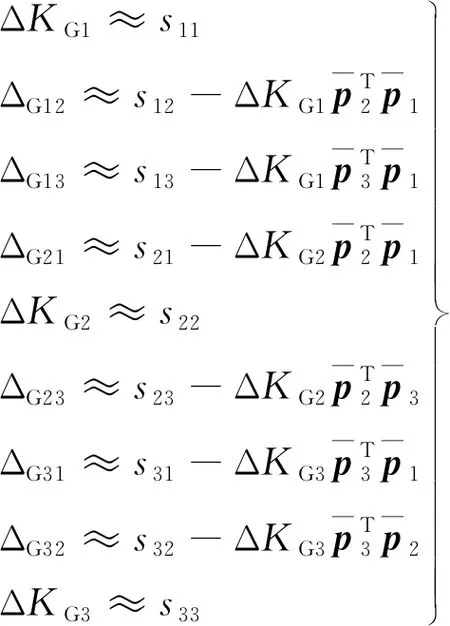
(19)

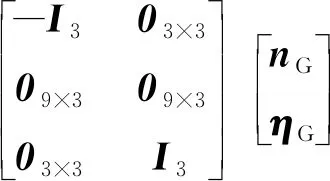
(20)

至此，濾波器的狀態變量、狀態方程和測量方程與原標定方法[4]相同，因此證明原標定方法是本方法在陀螺組件為正交安裝條件下的特例，因此完全可由本方法代替。

2 系統可觀性分析

當星體角速度ω為常值時，陀螺測量角速度誤差中與安裝誤差和刻度因子誤差相關的項也為常值。它們可以認為是等效的常值漂移，并且可由常規星敏定姿算法估計。以陀螺i為例，若令：

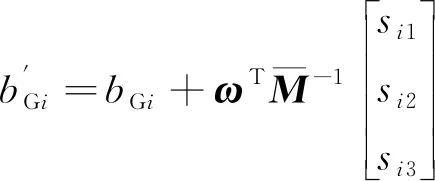
(21)

Axi=bi

(22)

式中：

式(22)有唯一解的條件是：

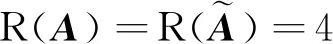
(23)

顯然式(23)的成立要求n>3。當n=4時，推導可知式(22)有唯一解的角速度組合條件是：

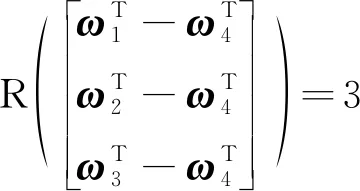
(24)

滿足該條件意味著系統輸出能夠完全反應系統狀態，因此式(24)是系統可觀的角速度組合條件。不難驗證當ω1、ω2和ω3非共面，且ω4為零或-ωi(i=1,2,3)時，式(24)成立。由此可見，航天器繞三個慣量主軸旋轉，再加上一個靜止狀態或是繞一個慣量主軸反向旋轉，就可以保證全部狀態可觀。對于噴氣控制的航天器，繞慣量主軸旋轉可以提高姿態機動的穩定性。

3 數學仿真結果

表1 仿真工況列表

工況1的仿真的結果見圖2～圖4。陀螺安裝誤差標定結果曲線見圖2，在前3個姿態機動段時標定誤差較大，在進入第4個姿態機動段時誤差迅速減小并收斂。陀螺常值漂移標定結果曲線見圖3，在仿真前20 s標定誤差變化幅度較大，然后迅速向零附近收斂。陀螺刻度因子標定結果曲線見圖4，其變化特點類似安裝誤差標定結果曲線。陀螺安裝誤差和刻度因子的標定誤差，在前3個姿態機動段，并不一定隨著姿態機動段數的增加而減小，但是在進入第4個姿態機動段后都會迅速向零收斂，這與可觀性分析結果一致。

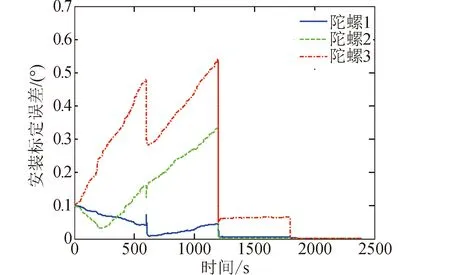
圖2 工況1的陀螺安裝誤差標定結果曲線Fig.2 Calibration error curves of gyro misalignment in case 1

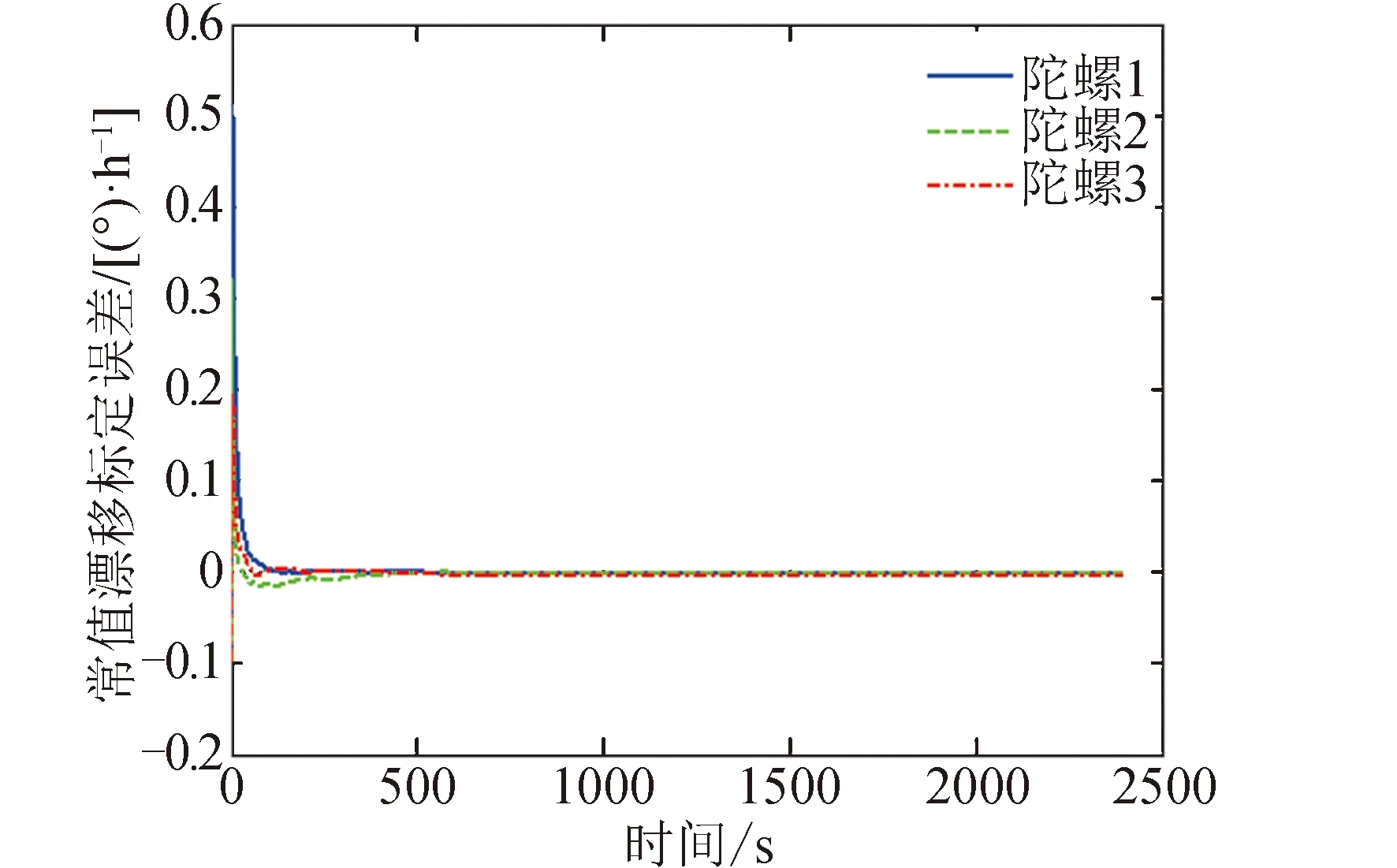
圖3 工況1的陀螺常值漂移標定結果曲線Fig.3 Calibration error curves of gyro constant bias in case 1

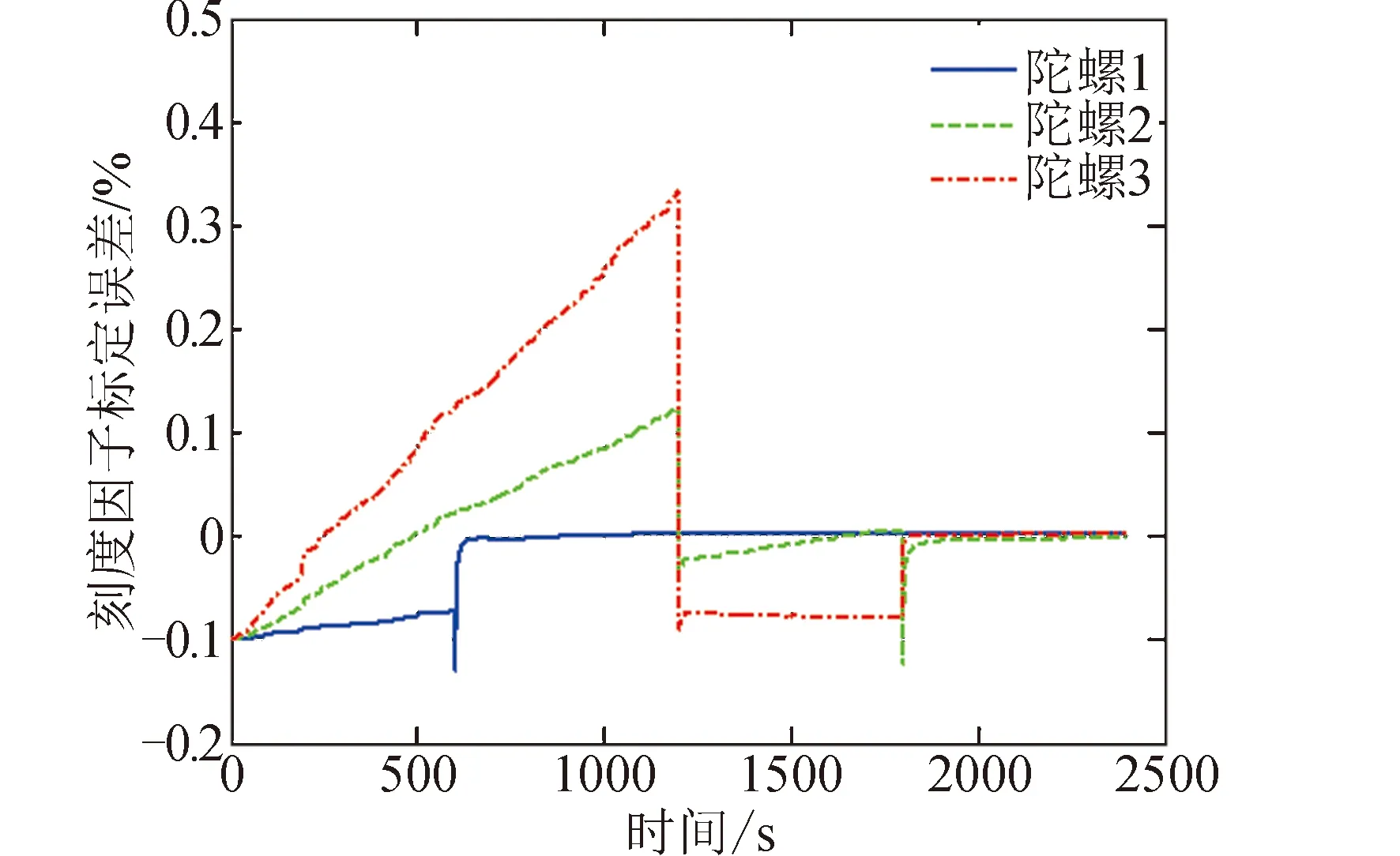
圖4 工況1的陀螺刻度因子誤差標定結果曲線Fig.4 Calibration error curves of gyro scale factor in case 1

工況2的仿真結果見圖5～圖7。從圖5和圖7可知陀螺安裝誤差和刻度因子的標定誤差，在進入第4個姿態機動段后迅速向零收斂。從圖6可知陀螺常值漂移的標定誤差，在進入第2個姿態機動段后迅速向零收斂，這比工況1要晚。工況2中所有標定誤差都能收斂再次驗證了可觀性分析結果。

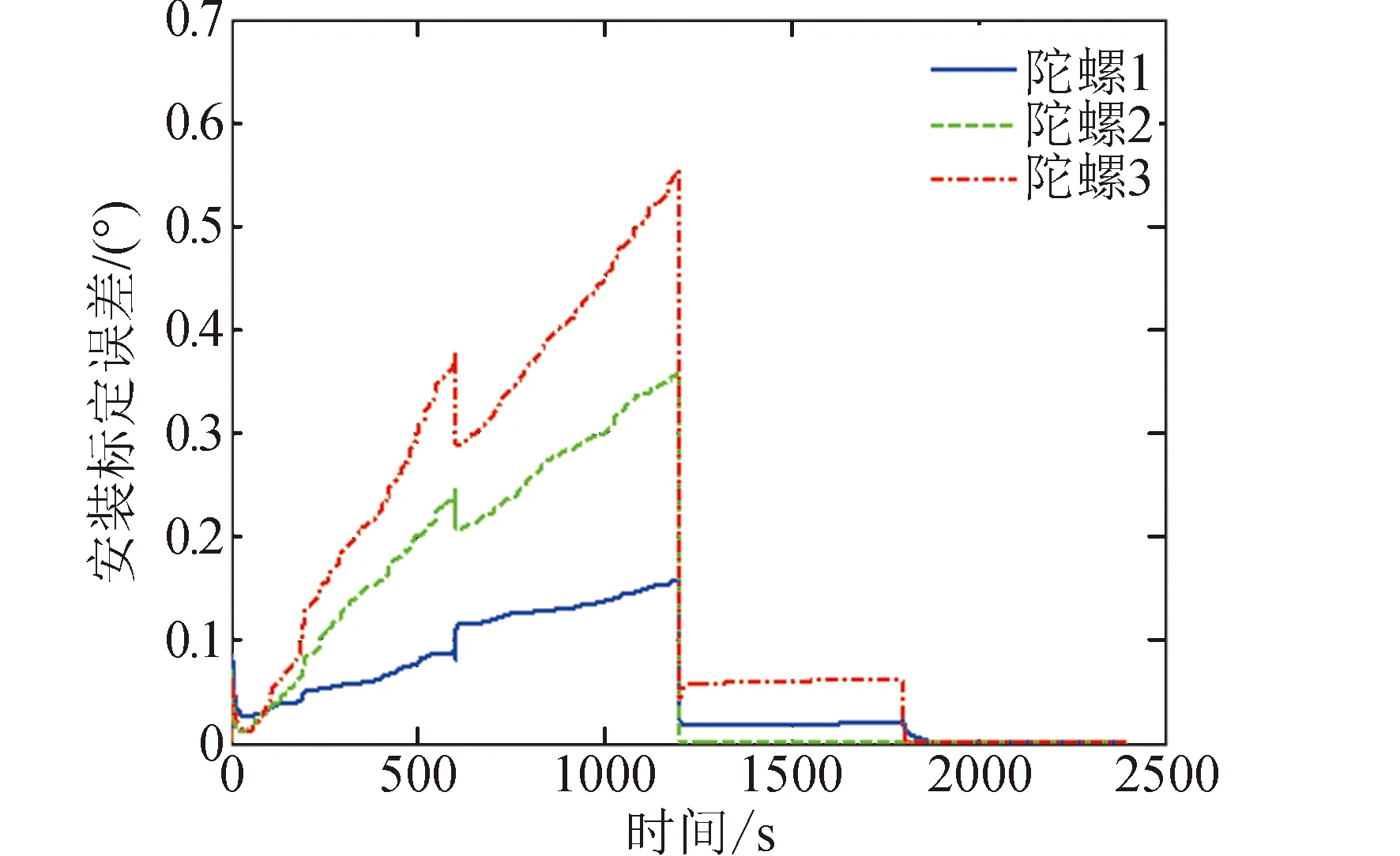
圖5 工況2的陀螺安裝誤差標定結果曲線Fig.5 Calibration error curves of gyro misalignment in case 2

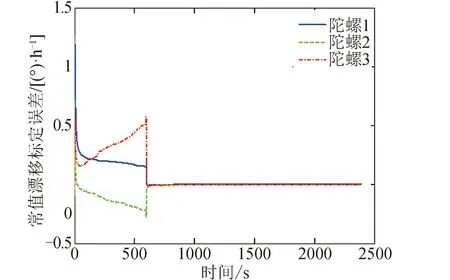
圖6 工況2的陀螺常值漂移標定結果曲線Fig.6 Calibration error curves of gyro constant bias in case 2

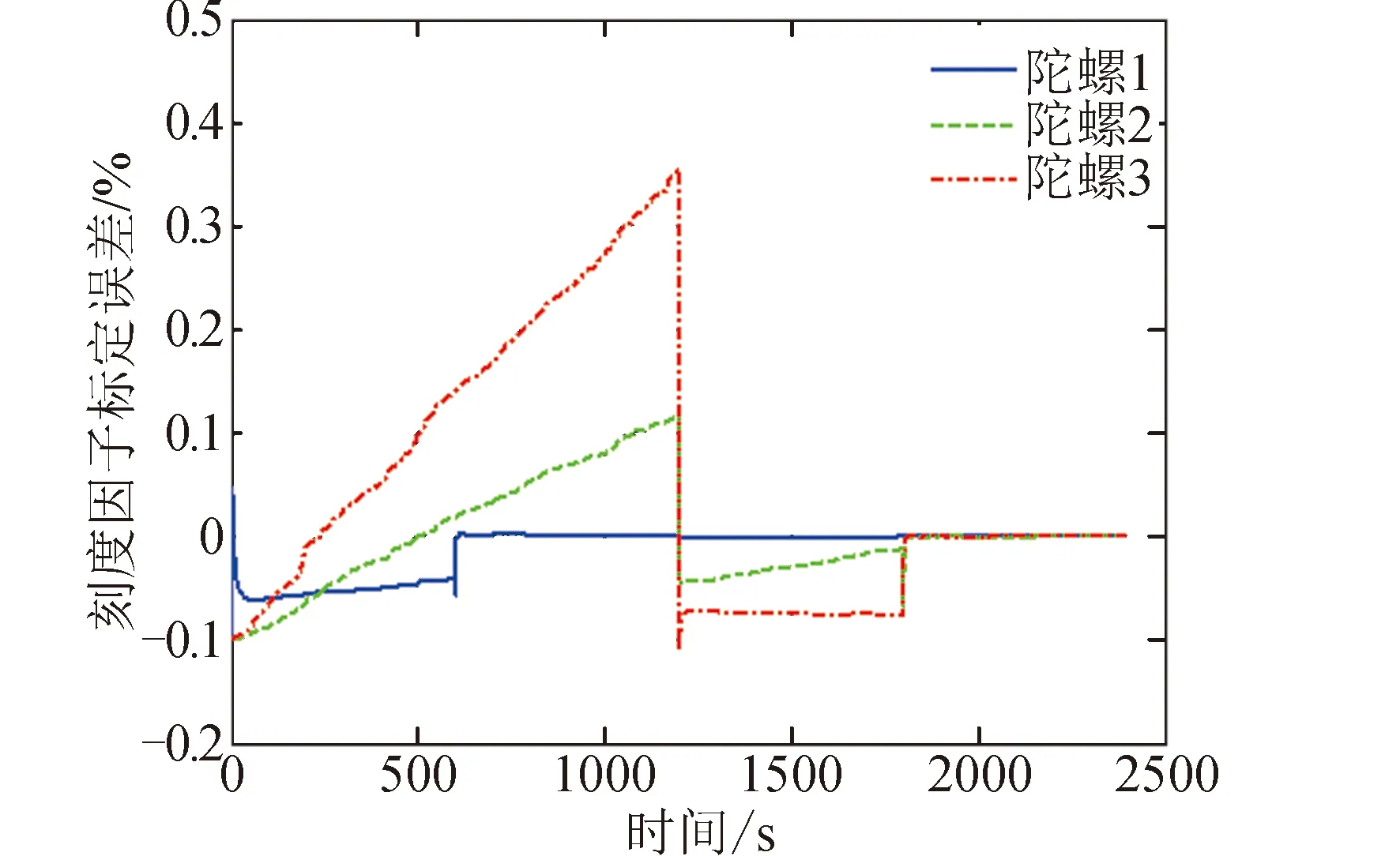
圖7 工況2的陀螺刻度因子誤差標定結果曲線Fig.7 Calibration error curves of gyro scale factor in case 2

工況3的陀螺參數最大標定誤差見表2。陀螺安裝誤差最大標定誤差為0.002 14°，是初始誤差的2.14%。陀螺常值漂移最大標定誤差為0.00966°/h，是初始誤差的9.66%。陀螺刻度因子誤差最大標定誤差為0.00462%，是初始誤差的4.62%。以上數學仿真結果表明本方法有效。

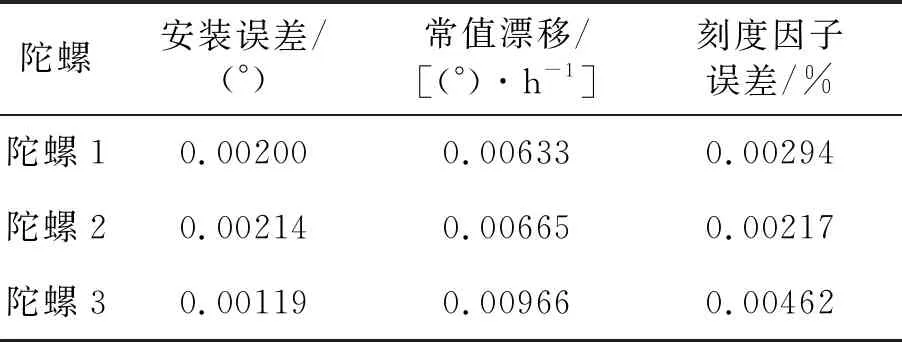
表2 工況3的陀螺參數標定結果

工況4的陀螺參數最大標定誤差見表3。陀螺安裝誤差最大標定誤差為0.001 64°，是初始誤差的1.64%。陀螺常值漂移最大標定誤差為0.00736°/h，是初始誤差的7.36%。陀螺刻度因子誤差最大標定誤差為0.00292%，是初始誤差的2.92%。表3結果優于表2結果，說明姿態機動方式2的標定精度高于姿態機動方式1。

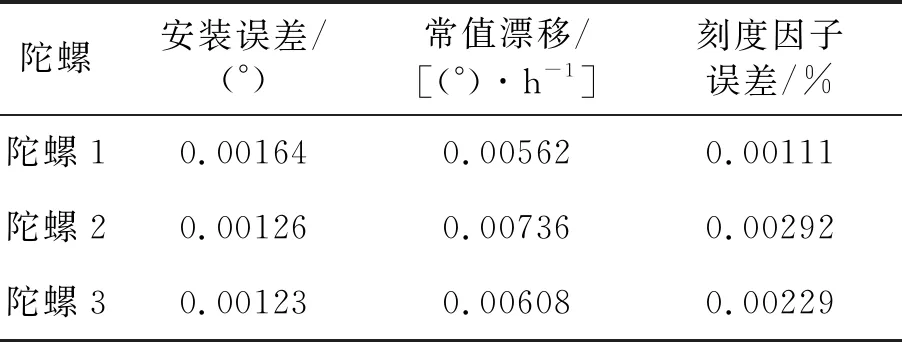
表3 工況4的陀螺參數標定結果

工況5的陀螺參數最大標定誤差見表4。

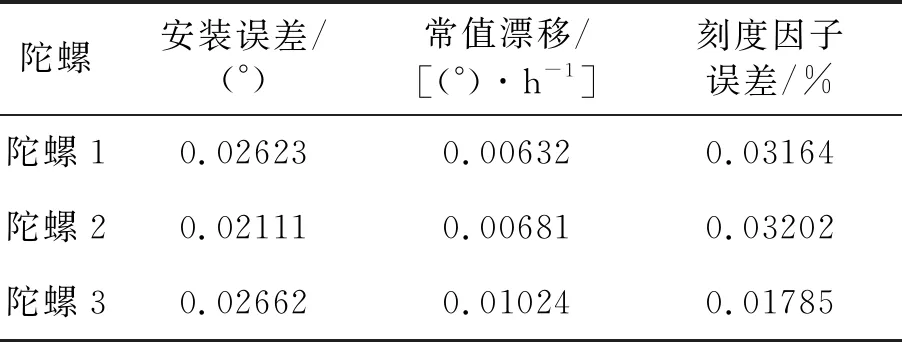
表4 工況5的陀螺參數標定結果

陀螺安裝誤差和刻度因子誤差的最大標定誤差相對表2增大一個量級，但是與表2工況的初始誤差相比，減小了一個量級。陀螺常值漂移最大標定誤差與表2相當。該結果說明陀螺初始安裝誤差增大，則陀螺安裝誤差和刻度因子誤差的標定誤差會增大，而陀螺常值漂移標定誤差無顯著變化。此外，如果再進行一輪迭代標定，可將標定精度提高到優于表2結果的水平。

4 結束語

對現有的正交安裝陀螺組件在軌標定方法進行改進，提出應用范圍更為廣泛的非共面安裝陀螺組件的安裝誤差、常值漂移和刻度因子誤差在軌自主標定方法。該方法不要求陀螺為正交安裝，不要求標定姿態機動高穩定度。公式推導證明，原方法是本方法在陀螺組件為正交安裝條件下的特例，因此完全可由本方法代替。給出的系統可觀的角速度組合條件可指導姿態機動序列的設計工作。數學仿真結果表明本方法有效，陀螺安裝誤差、常值漂移和刻度因子誤差標定精度分別優于0.01°、0.01(°)/h和0.01%。本方法對于有慣性導航需求的航天器設計具有重要的工程應用價值。