未知環境下移動機器人自主避障算法的研究

問澤藤，溫淑慧,*，張 迪

(1.燕山大學 智能控制系統與智能裝備教育部工程研究中心，河北 秦皇島 066004; 2.燕山大學 工業計算機控制工程河北省重點實驗室，河北 秦皇島 066004)

0 引言

自主避障能力是移動機器人進行路徑規劃必不可少的基本能力之一，研究早期的大部分學者致力于研究靜態的、單個障礙物的簡單情形[1-2]，并取得了不錯的成果，然而現實生活環境是非結構化且未知的，機器人對周圍環境的感知會因為各種干擾存在不確定性，如何在未知的非結構化環境中實現機器人高效的自主避障與目標導航，至今仍是一個研究熱點與難點。

隨著人工智能技術逐漸地發展，一種基于深度學習的避障算法被研究出來。這種算法旨在使機器人通過深度神經網絡來感知傳感器的傳輸數據,以學習控制策略。根據學者們的研究成果，可以將基于學習的避障算法歸結為兩類。第一類是通過智能學習訓練機器人學習控制策略。該類方法一般使用深度神經網絡對機器人避障問題進行建模，并通過大型數據集對其進行訓練[3-5]。但是這種方法在很大程度上依賴于大量涵蓋各種場景的訓練數據，并且它對環境變化的泛化能力較弱。第二種方法是使用端到端的深度強化學習(DRL)框架。ZHU等人[6]基于預訓練的ResNet構建了一個結合深度學習的Actor-Critic模型，實現離散三維環境中的機器人導航。TAI等人[7]通過連續的DRL算法訓練了一個端到端的策略，通過將10維激光數據和相對的目標位置作為輸入狀態來解決無先驗地圖信息的導航問題。XIE等人[8]建立了一個基于double DQN和dueling DQN機制的D3QN模型用于自主避障。KHAN等人[9]使用了帶有輔助獎勵和內存增強網絡的自我監督策略梯度架構來幫助機器人導航到目標位置。文獻[10]和[11]通過深度強化學習解決了機器人導航問題，并設計了具有長期短期記憶(LSTM)的神經網絡架構來記憶環境。然而深度強化學習算法在訓練時普遍存在收斂速度較慢問題，容易產生訓練失敗結果。

本文基于深度強化學習，對機器人的避障和導航問題進行了研究。針對基于全連接神經網絡的深度強化學習算法在訓練機器人避障時收斂速度較慢的問題，提出了基于長短期記憶網絡的近端策略優化避障算法。結合所設計的神經網絡結構和獎勵函數進行端到端的模型訓練，將二維雷達傳感器的感知數據、機器人的位置及期望目標位置等信息直接映射為機器人的連續動作指令，并設計有效的獎勵函數對動作指令進行評價，實現無先驗地圖信息情況下機器人在非結構化環境中的自主避障。

1 靜動態環境下避障算法研究

1.1 移動機器人建模

本節以非完整輪式差分驅動機器人Turtlebot3 Waffle Pi為研究對象，在具有靜動態障礙物的歐幾里得平面上，進行了機器人自主避障問題的研究。問題可描述如下：在t時刻，處于未知復雜的非結構化場景中的機器人通過雷達感知到部分環境狀態st，并試圖獨立探索安全穩健的策略πθ(at|st),進而計算出一個無碰撞可能性的動作at，最終規劃出不與任何障礙物碰撞的最佳軌跡，使其在更短的時間內從當前位置到達指定的目標位置g,并且不與行走途中的障礙物發生沖突，其中θ是策略參數。

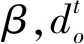
1.2 端到端的深度強化學習框架

本文所設計的端到端深度強化學習框架主要由以下三部分組成：

1) 狀態空間：移動機器人通過二維的激光雷達實現與周圍環境之間的交互。機器人的狀態向量st由傳感器所獲得的二維激光數據、當前位置的坐標、目標位置的坐標、當前的速度(包括線速度和角速度)和機器人的半徑組成，可表示為[lt,ct,g,vt,wt,R]。

2) 動作空間：機器人的動作空間包括線速度和旋轉速度，表示為運動命令at=[vt,wt]。在本研究中，考慮到機器人運動學和現實應用需求，對線速度和角速度范圍進行歸一化處理，將機器人線速度的范圍限定為vt∈[0,0.5]，角速度的范圍限定為wt∈[0,0.5]。

3) 獎勵函數的設計：獎勵函數是決定一個強化學習算法是否可以成功收斂的關鍵。本文的獎勵函數設計如下[12]：

(1)

1.3 基于長短期記憶網絡的近端策略優化避障算法

1.3.1 近端策略優化算法

近端策略優化算法(Proximal Policy Optimization，PPO)[13]是一種基于策略-評價架構(結構圖如圖1所示)的新型的深度強化學習算法，可以在多個訓練步數中實現小批量更新，解決了策略梯度問題中步長難以確定的問題，可以被用于離散和連續動作控制。本節選擇基于PPO算法來生成移動機器人自主避障和目標導航問題的最優控制策略。

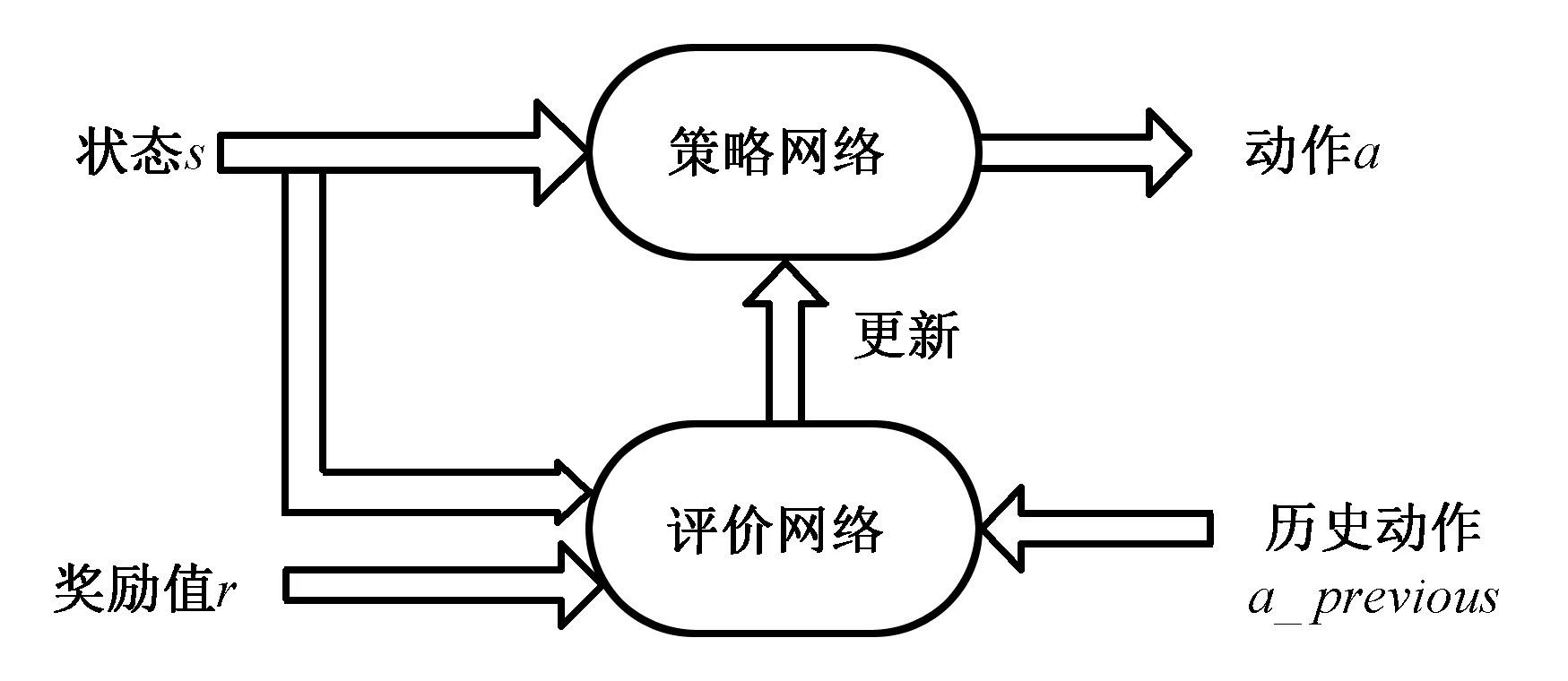
圖1 策略-評價算法結構示意圖Fig1 Structure diagram of Actor-Critic algorithm

基于策略-評價算法框架的策略梯度計算方法為[14]

(2)

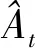
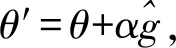
(3)

其中，θ代表更新前的策略參數，θ′代表更新后的策略參數,α表示新舊策略之間的參數更新步長。策略梯度算法對步長α十分敏感，如果α過大，則易發散；如果α太小，則訓練過程將會非常緩慢，算法將不易收斂。所以，不合適的步長α將會使算法將會難以學習到合適的策略。為了解決上面的問題，Shulman博士等人[14]提出信賴區域策略優化(Trust Region Policy Optimization，TRPO)算法。

TRPO算法為使累積獎勵單調不減，將參數更新后策略所對應的累積獎勵函數轉換為參數更新前策略所對應的累積獎勵函數與參數更新前后策略的獎勵差值之和的表示方法，當策略更新前后的參數變化很小時，參數更新后狀態分布的變化可忽略。算法使用了參數更新前策略對應的狀態分布代替了更新后策略對應的狀態分布，則可得到目標函數[14]：

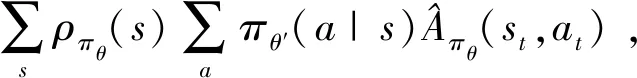
(4)

TRPO算法需要更新策略來最大化目標函數，為了避免策略更新時步長過大或者過小問題，對新策略和舊策略之間的KL散度施加約束[14]:

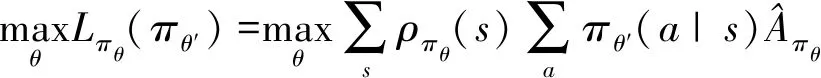
(5)

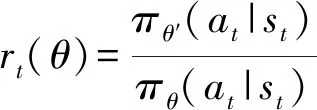
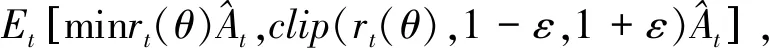
(6)

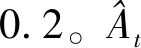
(7)

1.3.2 神經網絡結構

圖2是針對移動機器人自主避障問題設計的深度神經網絡控制策略結構圖。整個神經網絡具有兩個分支，策略網絡分支和評價網絡分支。兩個分支除輸出層外，其他均保持有相同的結構。

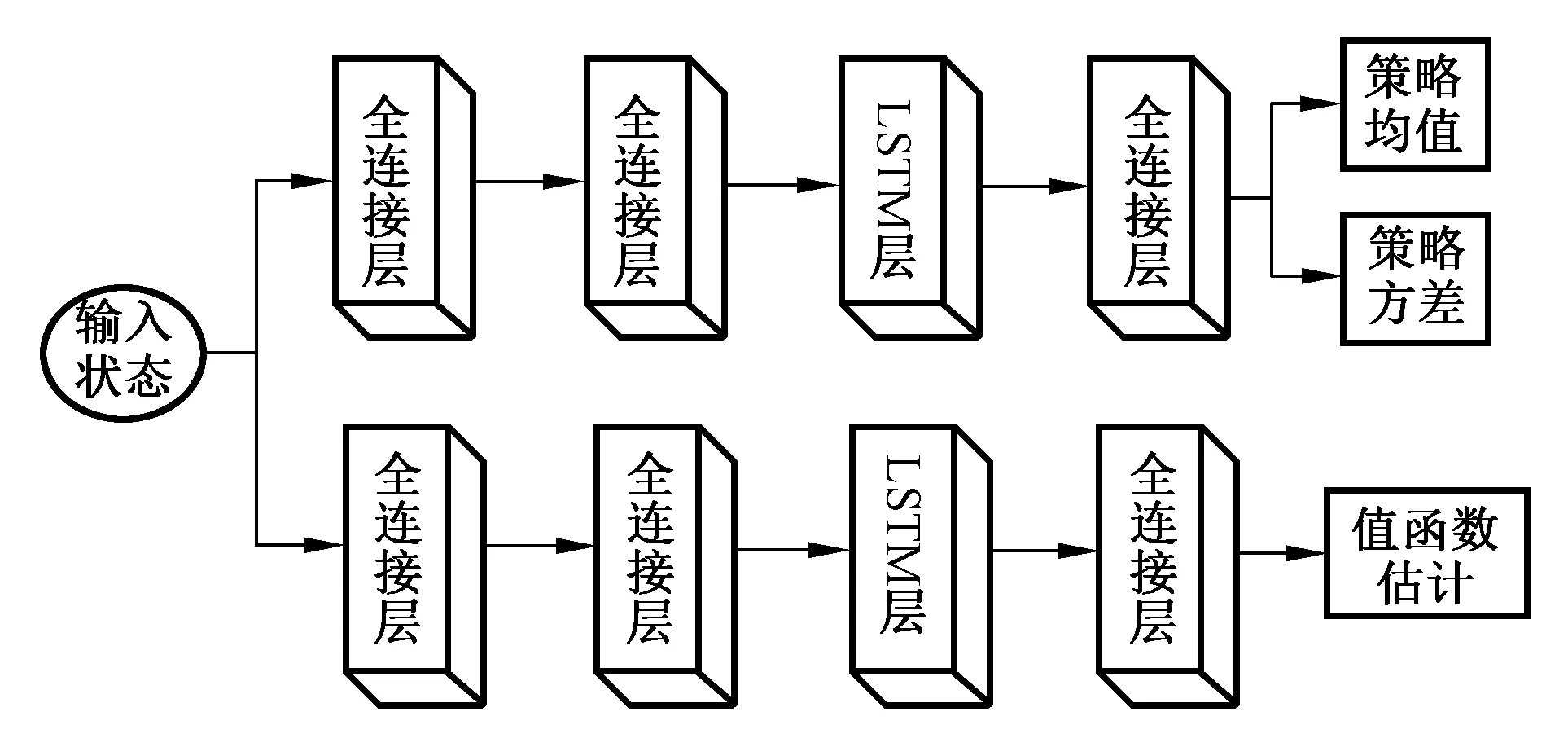
圖2 移動機器人自主避障系統全連接神經網絡控制策略結構圖Fig.2 Structure diagram of fully connected neural network control strategy for mobile robot autonomous obstacle avoidance system

將由機器人的狀態組成的一系列序列信息作為輸入向量，表示為st，輸入到第一隱藏層中進行特征提取。第一、第二、第四隱藏層均為全連接層，其中一二連接層使用ReLU非線性函數作為激活函數。為了使神經網絡可以做出更好的決策，在神經網絡結構中引入了長短期記憶網絡[15](Long Short Term Memory network, LSTM)作為第三隱藏層來更好地提取輸入向量的特征。利用LSTM的編碼和存儲功能來獲取一系列與時間相關的信息，使網絡可以考慮歷史的機器人狀態特征，從而可以探索出更適應于當前所處環境的策略。最后將第四隱藏層提取的特征輸入到輸出層。

策略網絡分支輸出當前策略估計的均值μθ和方差σθ，分別使用Tanh函數和Sigmoid函數作為激活函數，通過高斯分布N=(μθ,σθ)采樣， 獲得移動機器人的此時最優的線速度指令vt和角速度指令wt。評價網絡分支的輸出層只有一個神經元，輸出狀態值估計Vφ(st)。

2 仿真及實驗研究

2.1 仿真實驗條件

本文仿真實驗所用的系統環境為64位Ubuntu 16.04，采用機器人操作系統(Robot Operation System，ROS)中的Gazebo模擬器[8]搭建仿真環境，選擇Turtlebot3 Waffle Pi作為避障仿真研究所用的機器人模型。利用二維激光雷達獲取環境狀態，通過里程計獲取自身的位姿，計算當前所在位置的坐標。

整個訓練流程可分為兩個階段，階段一是通過執行策略來收集樣本數據，階段二是使用采集的樣本數據來更新策略參數，整個訓練過程在兩個階段之間交替進行。首先在樣本采集期間，機器人通過傳感器獲得輸入觀察狀態，利用神經網絡提取狀態特征并最終輸出策略，使用該策略可以獲得機器人當前時刻的動作指令并執行，環境產生新的變化，并通過對機器人反饋獎勵值，來刺激機器人通過新的輸入狀態生成下一個動作指令，將采集的樣本存儲到經驗集合中。使用神經網絡作為非線性函數逼近器獲得狀態值函數，用來估計優勢函數。循環執行上述過程直至訓練步數達到設置的策略更新最小批量值，訓練進入策略參數更新階段，利用經驗集合中的K個樣本更新參數，設置策略更新最小批量值的原因是為了更好地確定神經網絡策略梯度的下降方向。一次性采集K個樣本輸入到神經網絡的做法可以降低某單個錯誤的樣本對于策略梯度下降方向的影響，同時提高算法的抗干擾性，最終致使計算出的策略梯度下降方向能夠更加接近理想值，算法盡快地實現收斂。

迭代更新網絡的過程如下，首先將訓練樣本輸入至評價網絡，利用Adam優化器對損失函數進行優化，以更新評價網絡的參數。之后將訓練樣本輸入到策略網絡中，同樣利用Adam優化器去更新策略網絡的參數。表1為訓練算法時算法所設置的超參數。

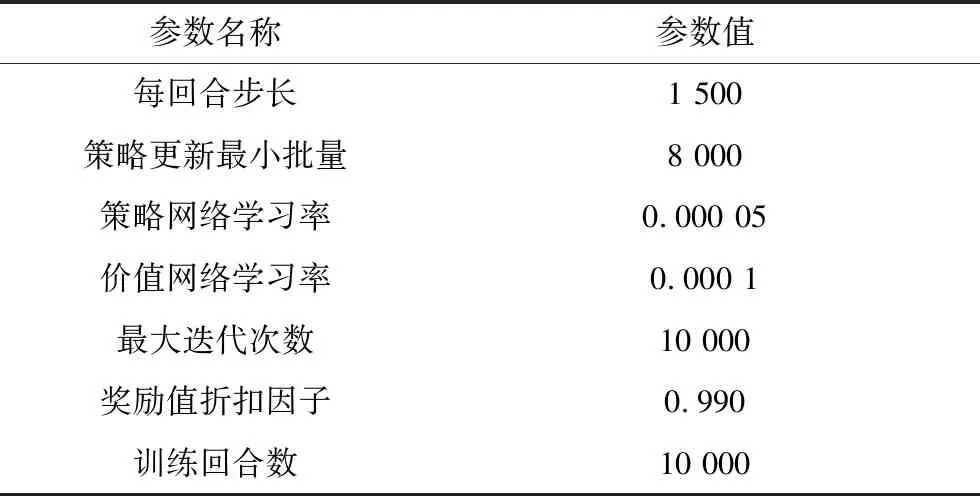
表1 超參數設置表Tab.1 Settings of hyperparameter value

本文主要針對無障礙場景以及多個動態障礙物場景進行模型訓練，考慮到在實際應用中，存在障礙物為不規則形狀的情況，設置了其他形狀障礙物來測試算法性能。

2.2 無障礙場景

首先，無障礙場景仿真環境如圖3所示，四周部分為4 m×4 m的墻體，左上角方形部分為目標點。在進行機器人訓練的過程中，若機器人到達目標位置后，目標位置將會隨機改變，機器人將會向新的目標位置繼續探索。

圖3 Gazebo移動機器人無障礙仿真環境Fig3 Robot obstacle-free simulation in Gazebo

分別使用引入LSTM[15]前后的神經網絡進行模型訓練。如圖4(a)為使用基于全連接神經網絡的避障算法訓練移動機器人在無障礙物環境中實現目標導航時，每個回合的累積獎勵的收斂曲線，圖4(b)為使用基于LSTM的神經網絡的避障算法訓練結果。隨著訓練步數的增長，獎勵值逐漸上升，在圖4(a)中，訓練到1 200步左右時，獎勵值達到平穩，算法逐漸收斂，在圖4(b)中，訓練500步左右時，算法逐漸收斂。結果表明引入LSTM可以使避障算法加快收斂。

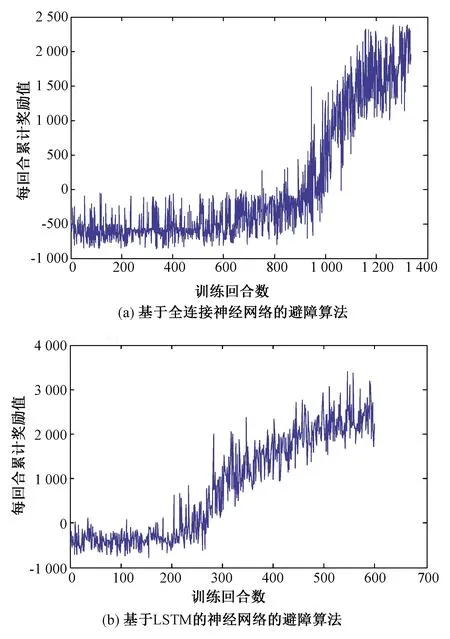
圖4 無障礙場景下獎勵值曲線圖Fig.4 Curve of rewards in obstacle-free scene

在算法收斂后，為了測試訓練出的模型的性能，在場景中隨機設置了幾個目標點(用圓圈表示，其中序號代表目標點順序)，使用訓練出的模型控制機器人來實現在無障礙訓練場景中的自主行走。圖5(a)為機器人在Gazebo模擬器中進行路徑規劃生成的軌跡圖，可以看出機器人成功到達了所設置的目標點且沒有與墻體發生碰撞。

基于本文進行的研究，可以與SLAM建圖算法進行融合，實現對未知環境的自主建圖。圖5(b)為機器人在進行路徑規劃的同時對環境構建的地圖，將Gmapping算法與本章的自主避障算法整合為一個框架，使處于未知環境的機器人實現目標導航并且同時自主完成對環境地圖的構建。

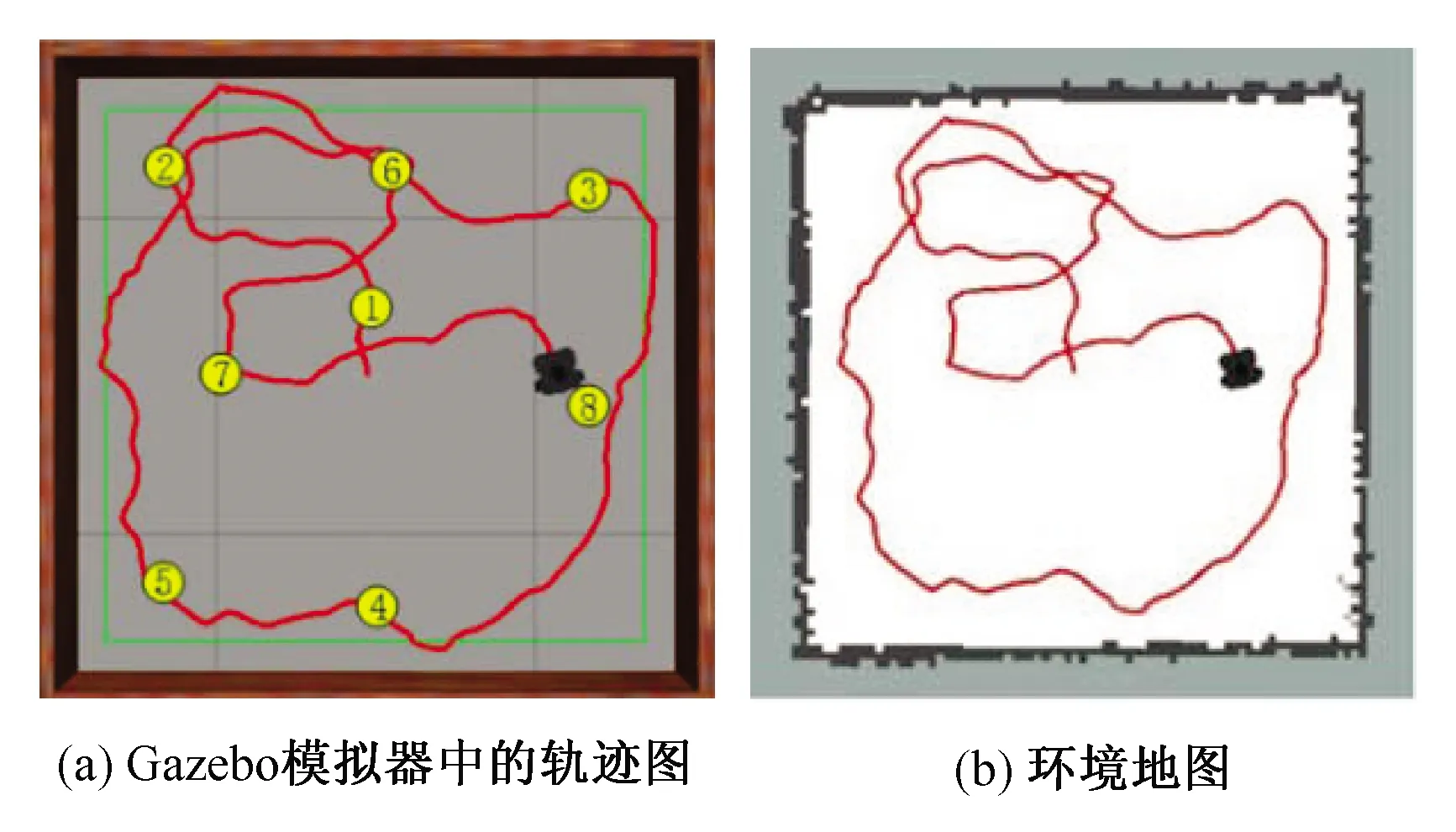
圖5 無障礙場景下的移動機器人軌跡圖Fig.5 Robot trajectory diagram in obstacle-free scene

2.3 有障礙場景

圖6(a)為只具有靜態障礙物的仿真環境，其中，四周部分為4 m×4 m的墻體，4個圓柱為靜態障礙物，左上角正方形為機器人的目標點。圖6(b)為具有動態障礙物的仿真環境，其中，墻體內使用4個順時針旋轉的圓柱作為動態障礙物，同樣正方形為目標點。本節使用基于LSTM神經網絡的近端策略優化算法進行訓練。

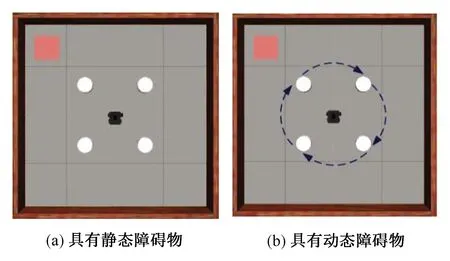
圖6 Gazebo機器人有障礙物仿真環境Fig.6 Simulation environment with obstacles in Gazebo

不同于無障礙物環境下的機器人訓練過程，此環境中增添了靜動態障礙物，當機器人與障礙物最短距離小于某一固定閾值時，即該次訓練迭代結束，進入下一次迭代。并且在路徑規劃過程中同時利用Gmapping建圖算法進行周圍環境地圖的構建，實現機器人的自主建圖。

如圖7(a)所示，不規則曲線即為機器人的行走軌跡，在路徑規劃過程中，成功避開了圓柱狀的靜態障礙物，并且依次到達了隨機設置的幾個目標位置。同時，在具有靜態障礙物的未知環境下，通過將Gmapping算法與本章的自主避障算法整合，同樣可以使機器人在進行路徑規劃的同時實現對環境的自主建圖。圖7(b)展示了機器人行進的軌跡和自主對環境構建的地圖。

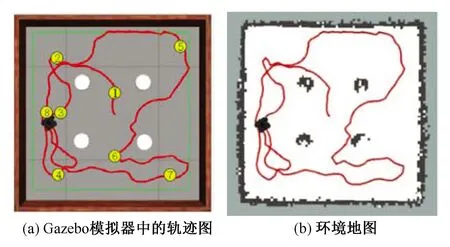
圖7 具有靜態障礙物的場景下移動機器人的軌跡圖Fig.7 Trajectory diagram of the mobile robot in scene with static obstacles

將圖6(a)所示環境中訓練完成的模型遷移到如圖6(b)所示的動態仿真環境中繼續訓練，則經過少量迭代步驟之后，機器人便可以在動態環境中實現自主避障及目標導航。如圖8(a)所示，機器人可逐次到達每個目標點。圖8(b)為機器人在規劃路徑到達各個目標位置的過程中，同時利用Gmapping算法構建的某時刻的二維環境地圖。

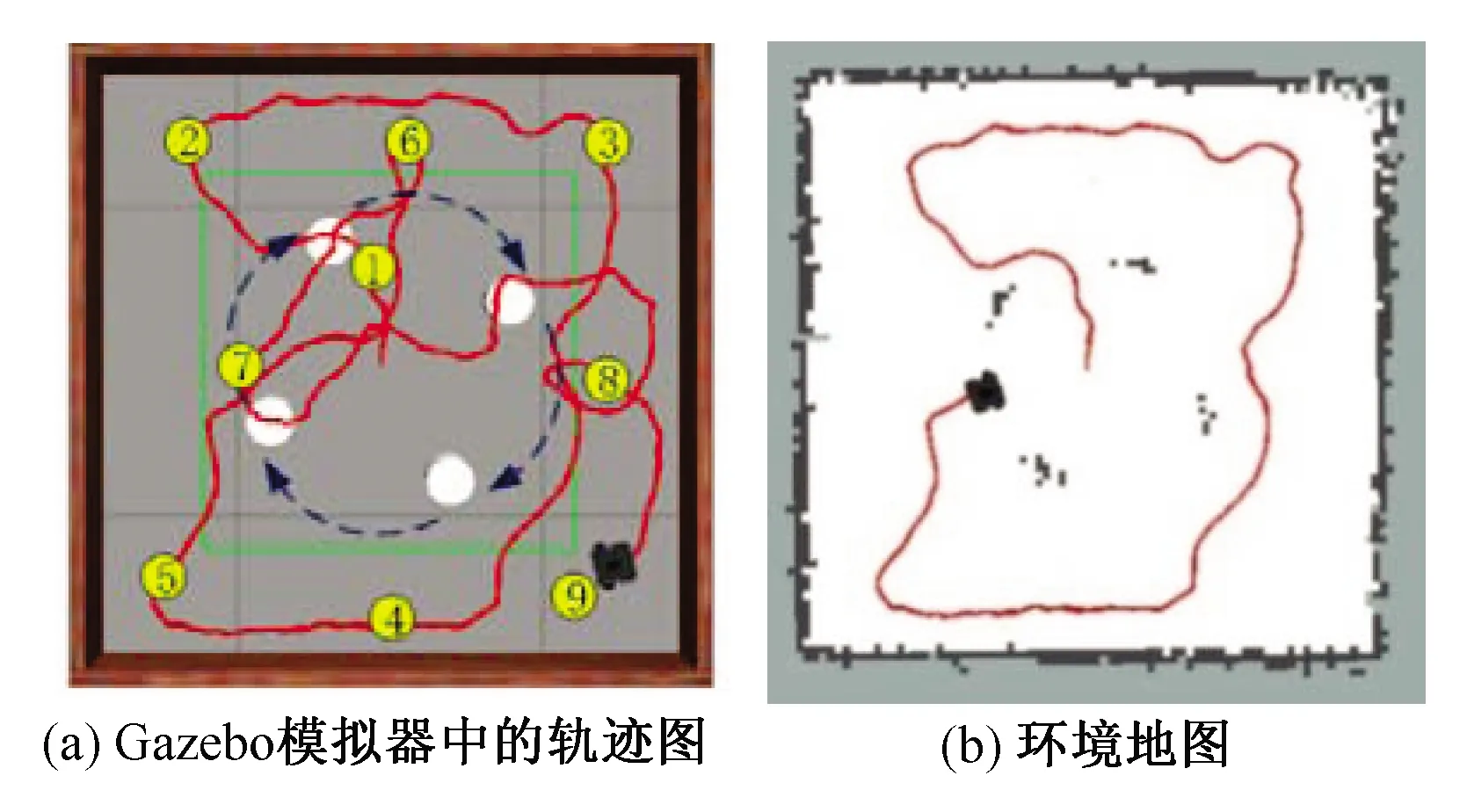
圖8 具有動態障礙物的場景下移動機器人的軌跡圖Fig.8 Trajectory diagram of the mobile robot in scene with dynamic obstacles

處理形狀多樣性的障礙物的能力是評估避障策略性能的重要指標。為驗證所提算法對于其他形狀障礙物的避障能力，將學習到的策略應用于其他情形。在Gazebo模擬器中設計了如圖9(a)所示的靜態仿真環境和圖9(b)所示的動態仿真環境，圓柱是動態障礙物，按照虛線的箭頭方向移動，其他形狀物體為靜態障礙物，包括方形木塊、長條墻體、圓桶等，并且在環境中隨機設置了幾個目標位置。通過圖中呈現的實線軌跡，展示了機器人最終成功規劃路徑依次到達了目標位置，而不曾與障礙物發生沖突，這表明通過所提算法學習到的策略具有避開其他形狀障礙物的能力。

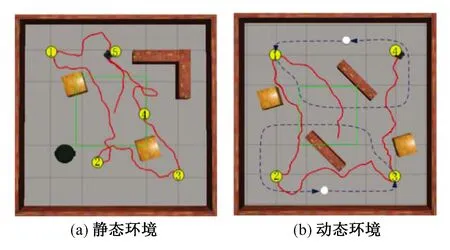
圖9 具有其他形狀障礙物的仿真環境下移動機器人的軌跡圖Fig.9 Trajectory diagram of mobile robot in simulation environment with obstacles of other shapes

2.4 對比實驗

為更好地展現所提出的算法性能，將其與基于D3QN[8]的避障算法進行對比。

首先在圖3的無障礙環境中進行對比訓練，可得如圖10的變化曲線。根據圖10可以看出， D3QN算法在約200回合時獎勵值上升，直至450回合時不再有上升趨勢，但是獎勵值上升過程中，會有許多突然下降的情況，這表示機器人發生碰撞。由此可以看出，相比于基于PPO[13]的算法，基于D3QN的算法可以使機器人實現目標導航，但難以學到穩定有效的避障策略。

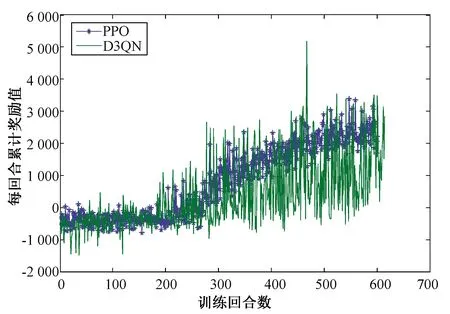
圖10 無障礙環境下基于D3QN算法和基于PPO算法訓練機器人時的獎勵值變化曲線對比圖Fig.10 Comparison of the change curve of reward value based on D3QN algorithm and PPO algorithm in the obstacle-free environment

在圖9(a)中的仿真環境中對兩種算法進行了訓練，繪制每回合累計獎勵值曲線，結果如圖11所示。從圖11可以看出，D3QN算法的獎勵值在1 400回合左右有上升趨勢，但仍存在較多負獎勵值，說明D3QN算法可以使機器人到達指定目標位置，但無法保證不發生碰撞，而改進后的PPO算法在2 000回合左右實現收斂，可以使機器人學會躲避障礙物，安全導航至目標位置。

使用Turtlebot2機器人對本文提出的避障算法進行了實驗驗證。圖12為Turtlebot2在具有靜態障礙物的場景下進行自主避障的過程。

圖12(a)中將長方形紙箱作為靜態障礙物，圖12(b)中將人作為靜態障礙物。結果顯示機器人可以通過改進后的PPO算法模型實現自主避障。

如圖13所示，是動態環境下移動機器人的自主避障過程，分別將人、紙箱和人依次作為動態障礙物，從圖中可以看出當動態障礙物出現在機器人感知范圍內，機器人能避開障礙物繼續行走。

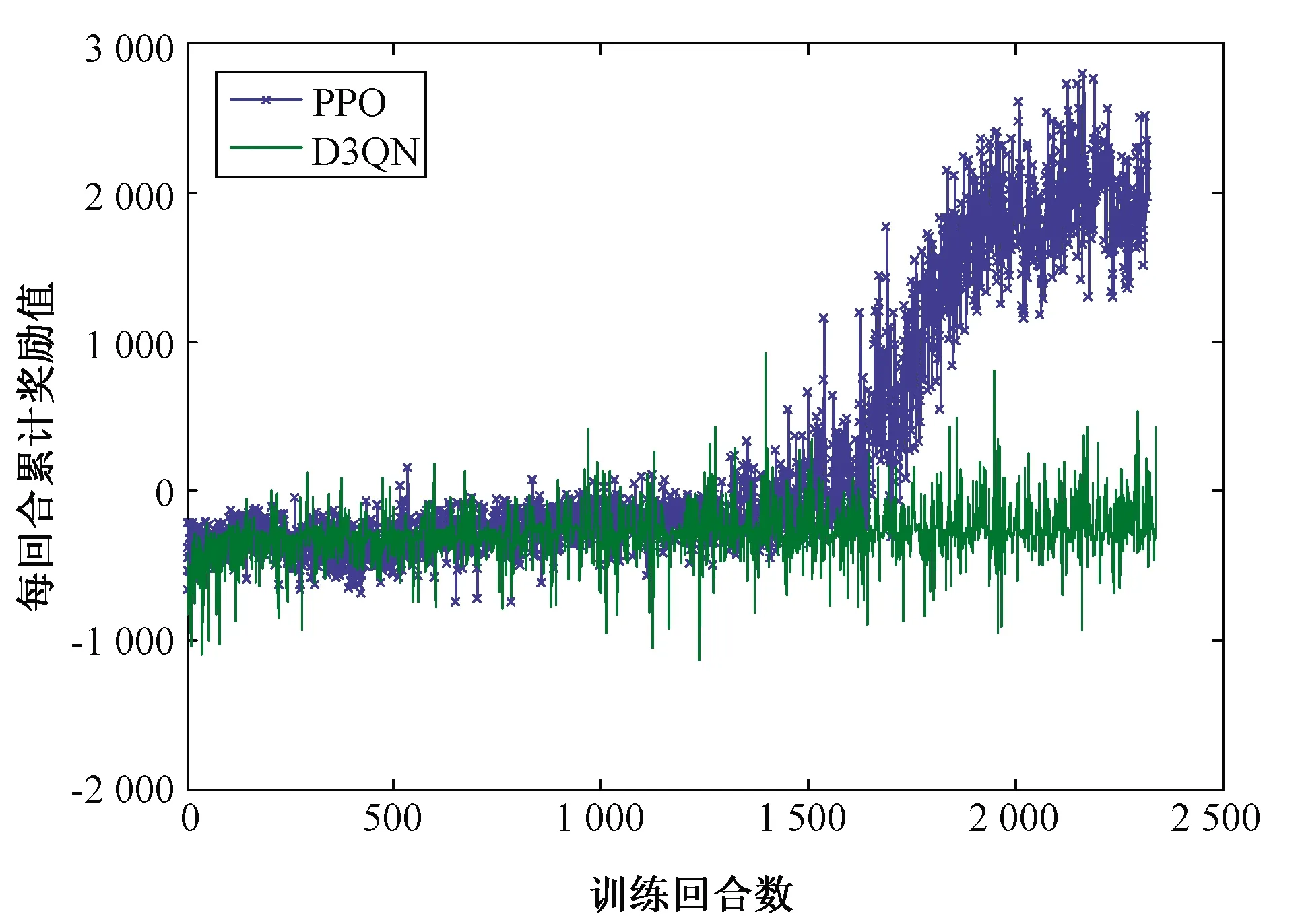
圖11 有障礙環境下基于D3QN算法和基于PPO算法訓練機器人時的獎勵值變化曲線對比圖Fig.11 Comparison of the curve of reward value based on D3QN algorithm and PPO algorithm in the obstacle environment

圖12 Turtlebot2機器人靜態環境下的避障實驗Fig.12 Obstacle avoidance experiment of Turtlebot2 robot in static environment

3 結論

本文針對移動機器人在具有動靜態障礙物的環境下的自主避障問題，提出了基于LSTM網絡的近端策略優化避障算法。根據機器人自主避障運動學模型設計端到端的深度強化學習框架，進一步引入長短期記憶網絡到全連接神經網絡中，使機器人更快地學習到有效的策略。仿真結果表明，引入LSTM的近端策略優化避障算法具有更快的收斂速度，并且比基于D3QN的避障算法成功率更高。最后在機器人平臺Turtlebot2上對所提出的避障算法進行了實驗驗證，實驗結果表明在靜動態環境中可以實現機器人無碰撞行走并到達指定的目標位置。

圖13 Turtlebot2機器人動態環境下的避障實驗Fig.13 Obstacle avoidance experiment of Turtlebot2 robot in dynamic environment