有理函數的迭代根

劉曉華，羅天琦

(1.樂山師范學院 數理學院，四川 樂山 614000；樂山師范學院 教師教育學院，四川 樂山 614000)

0 引言

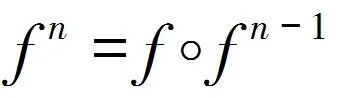
映射的迭代和迭代根有著密切的聯系，有時可以通過一映射的n次迭代找到它的n次迭代根。早在十九世紀數學家們就開始了對映射迭代根的研究[1-3]，但是直到二十世紀五六十年代才取得了突破性的進展[4-5]，其獲得的結果主要是針對區間上單調連續自映射的。對于在區間上非單調的連續自映射其迭代根問題要難得多。文獻[6]和[7]討論了一類特殊的非單調連續自映射，就是只有有限個非單調點的連續自映射，稱為嚴格逐段單調自映射，簡稱為PM-映射。對這類映射迭代根的研究，目前也取得了較大進展[8-14]。對于在區間上非單調不連續自映射的迭代根問題，到現在為此，研究甚少[15-16]。

在文獻[17]中，我們研究了有理函數

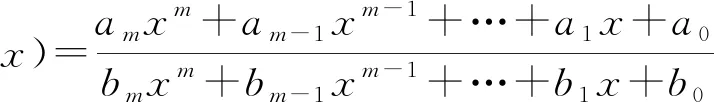
(1)

(2)

(3)

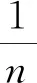
注：這篇文章中研究的函數都假定是有定義的，并且假定下文函數的迭代，也就是函數的復合都能進行。

1 有理函數的迭代根

在給定理之前我們首先給出下面要使用的由(3)定義的單項式的n次迭代公式

(4)

由歸納法，我們很容易得到上述公式。

定理假定hp(x)和Mk(x)分別由(2)和(3)定義。由(1)定義的有理函數Fm(x)的系數滿足

其中，n是一個使f(x)有意義正整數，或者有n次迭代根

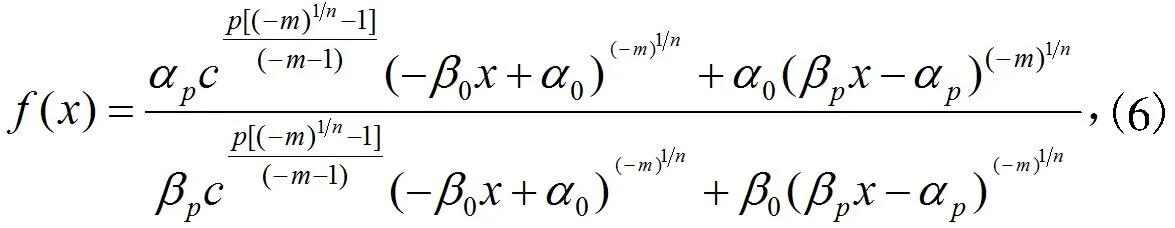
其中，n是一個使f(x)有意義正奇數。

證明 如果Fm(x)的系數滿足

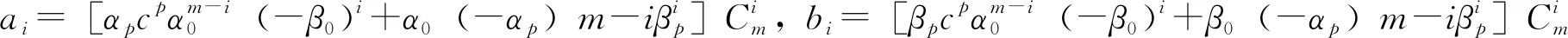
(7)

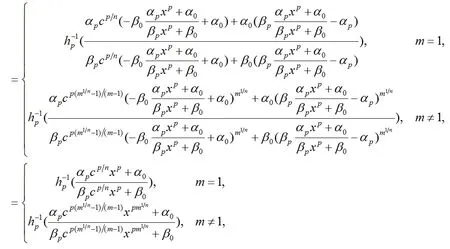
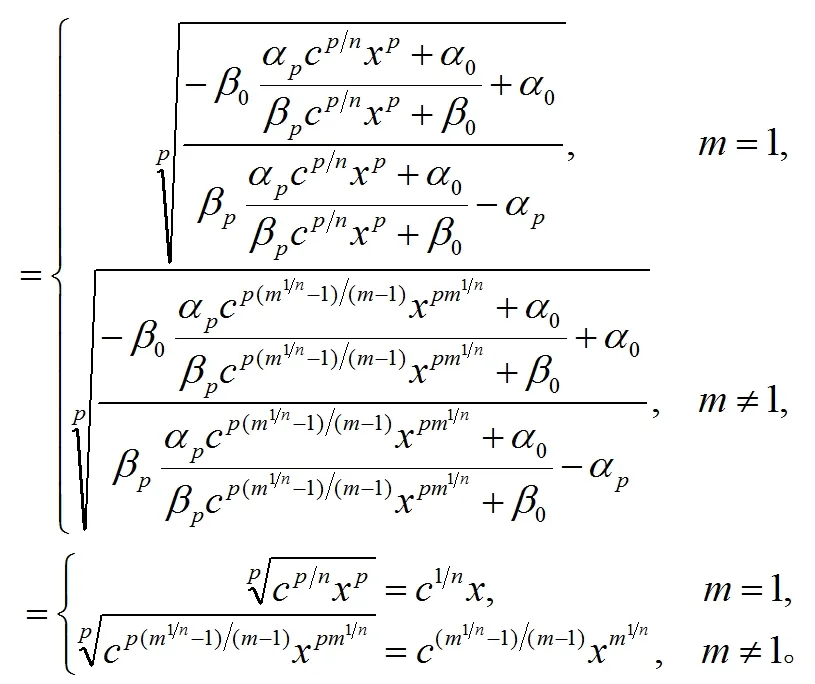
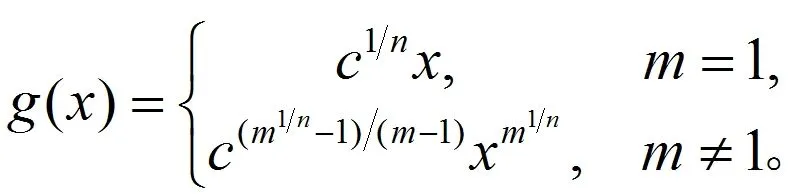
(8)

由公式(4)我們得到g(x)的n次迭代為

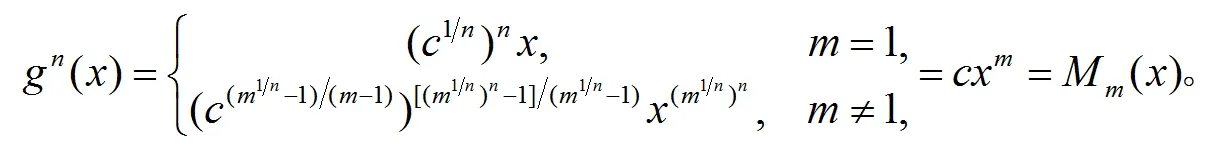
由(8)我們有

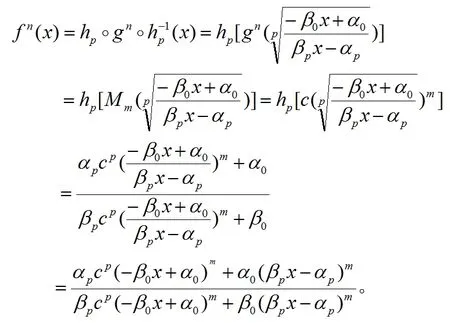
由(7)我們得到fn(x)=Fm(x)。因此，Fm有由(5)定義的n次迭代根f。

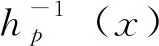
(9)

由公式(4)我們得到g1(x)的n次迭代為

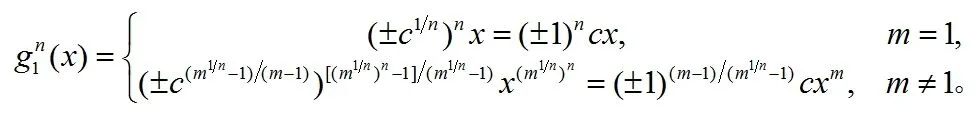
由(9)我們得到

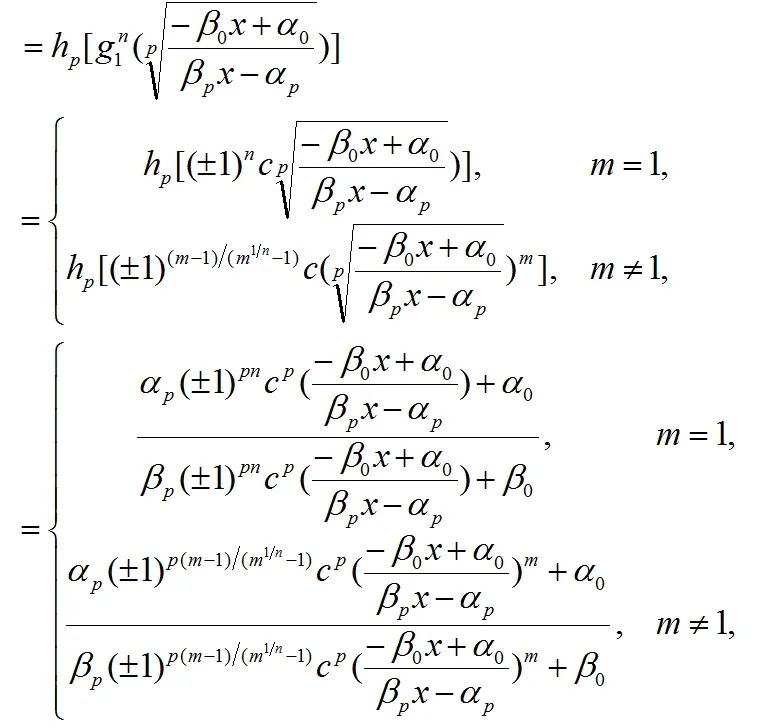
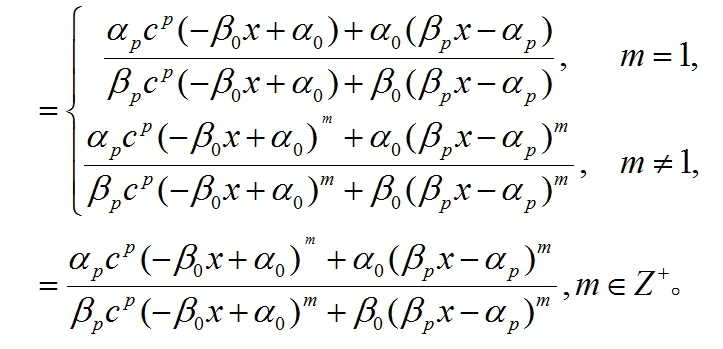
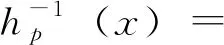
其次，我們證明(1)定義的有理函數Fm(x)的系數滿足

和

時，其中i=0,1,2,…,m。在(2)定義的橋函數hp(x)下，Fm(x)有由(6)定義的n次迭代根f。注意，n是一個正奇數。根據Fm(x)的系數滿足的條件，將其代入(1)我們得到

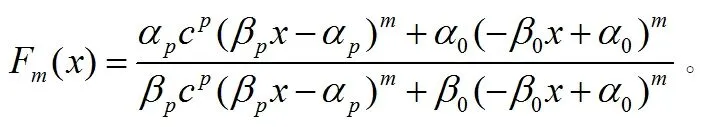
(10)

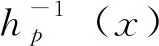
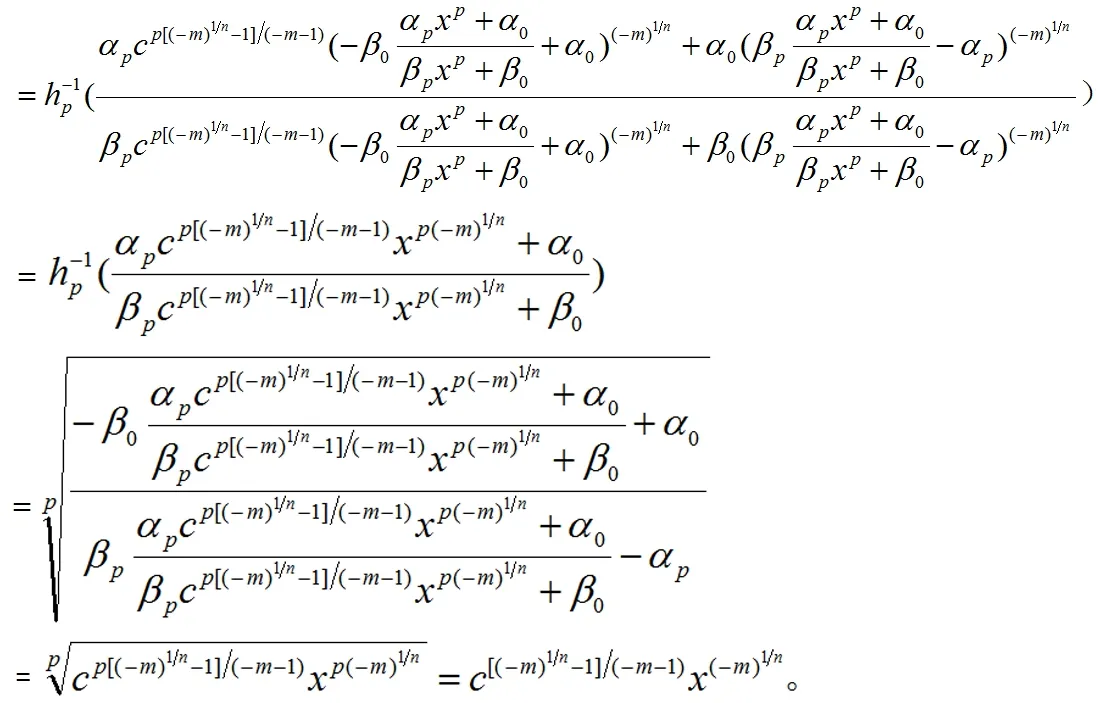
令g2(x)=c[(-m)1/n-1]/(-m-1)x(-m)1/n， 于是我們有

(11)

由公式(4)我們得到g2(x)的n次迭代為

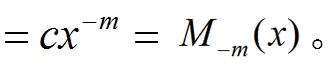
由(11)我們有

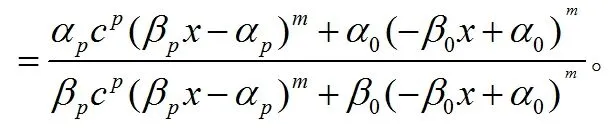
由(10)我們得到fn(x)=Fm(x)。因此，Fm有由(6)定義的n次迭代根f。

當p是一個偶數時，假定f由(6)定義，我們用一個與上面類似的討論，就能得到

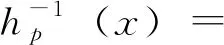
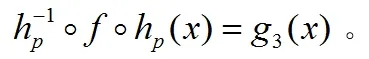
(12)

由公式(4)我們得到g3(x)的n次迭代為

由(12)我們有

由(10)我們有fn(x)=Fm(x)。因此，Fm也有由(6)定義的n次迭代根f。注意，n是一個使f有意義的正奇數。否則，f沒有定義。因此，這完成了定理的證明。

2 定理的應用

下面我們通過一些例子來展示定理的應用。

，

其中，n是使f1有意義的一個正整數。