基于負荷與風電出力場景集的運行備用動態調度方法

黃鵬翔，周云海，徐 飛，崔 岱，葛維春，陳曉東，李 鐵，姜 楓

（1.三峽大學 電氣與新能源學院，湖北 宜昌443002；2.清華大學 電機工程與應用電子技術系，北京100084；3.沈陽工業大學 電氣工程學院，遼寧 沈陽110870；4.國網遼寧省電力有限公司，遼寧 沈陽110004）

0 引言

風電等大規模可再生能源并網，為電力系統帶來了更多不確定性，增加了運行備用容量需求[1]～[3]。傳統電力系統備用決策方案通常以系統最大機組容量或者負荷的百分比確定每個小時電力系統備用需求。這種方法將機組出力與備用決策依次進行序列調度，沒有考慮機組出力和備用決策之間的量化關系，難以實現全局最優[4]。

為了平抑風電帶來的不確定性，有學者提出發電與備用協調調度模型，該模型將機組出力和備用決策聯合描述成一個帶有約束的優化問題，在滿足可靠性約束的同時，得到最優解。文獻[5]提出期望切負荷比例指標，量化每小時最小允許切負荷，但未考慮風電不確定性和備用成本，難以得到最優解，不能滿足經濟性的要求。文獻[6]研究了風電并網及其預測誤差對電力系統調度的影響，但在備用決策方面采用確定性方法，未計及風電波動性對備用需求的影響，約束條件過于簡單，使其結果不具有代表性。文獻[7]以失負荷期望損失和機組運行費用最小為目標，實現旋轉備用最優配置，但該方法中的備用與機組出力是分別優化，難以保證整體結果最優。文獻[8]在風電高滲透率的情況下，實現了機組出力和旋轉備用協調優化，但是缺少對系統可靠性與備用容量之間的量化分析。文獻[9]引入序列運算理論來處理可再生能源出力偏差和負荷偏差，大量的卷積運算加大了求解難度，且得到的場景不具有代表性。

本文根據風電和負荷預測誤差，利用拉丁超立方抽樣和同步回代縮減法，得到具有代表性的離散場景集，選擇每小時失電量期望和每小時棄風電量期望作為電力系統可靠性指標，推導每小時備用與可靠性指標之間的量化關系，得到每小時系統備用需求。計及網絡安全約束，建立以系統可靠性最高，運行成本最小和備用成本最小的發電與備用協調優化模型，優化每個小時運行備用需求和最優機組分配方案。在IEEE-30節點系統上驗證本文方案的有效性，分別量化每小時上調備用和下調備用需求容量，利用Matlab軟件調用Yalmip工具箱進行求解。

1 不確定場景描述

1.1 機組不確定性

本文只考慮停運1臺機組的場景。假設系統中有N臺機組，且每臺機組只有正常運行和強迫停運狀態，機組強迫停運概率模型按0，1分布，建立N-1機組故障場景集，每種場景的概率為[10]

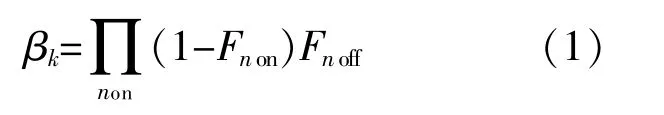
式中：non為正常運行機組編號；noff為故障機組編號；F為機組強迫停運率。

1.2 風電不確定性

本文采用場景法描述風電出力不確定性。將風電功率預測誤差視為服從期望為0，方差為正態分布的隨機變量，風電場實際出力為風電預測出力與風電預測誤差之和，其表達式為[11]

1.3 負荷不確定性

負荷預測也具有一定誤差。實際負荷出力可以表示為負荷預測值與負荷預測誤差之和，負荷預測誤差服從期望為0，方差為δtW2的標準正態分布，其表達式為[12]

1.4 場景生成與縮減

1.4.1 拉丁超立方抽樣

拉丁超立方抽樣方法（Latin Hypercube Sampling，LHS）基于分層抽樣原理，可以使隨機變量有效覆蓋整個分布空間[13]。因此，本文在生成風電場景和負荷場景時，采用拉丁超立方采樣的場景生成法。

1.4.2 同步回代縮減法

通過LHS方法可得到大量概率相同的時序場景，這樣可以更精確地描述風電和負荷的不確定性，但風電場景和負荷場景的組合會使場景數量急劇增加，使得計算效率低下，導致系統優化困難，所以本文采用基于同步回代縮減法對風電和負荷時序場景進行縮減，并且得到每個場景的概率[14]。其步驟如下：①首先得到大規模場景W={w1，w2，…，wn}，設置須要刪除的場景數量為K；②計算每一對場景的坎托洛維奇距離，即：

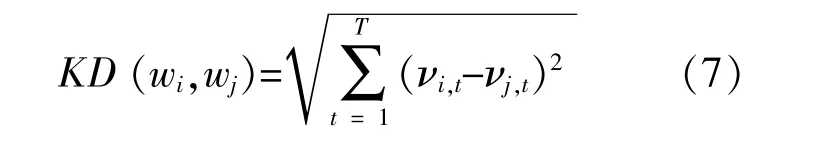
式中：wi為第i個場景；wj為第j個場景；νi，t為場景i的第t個元素；νj，t為場景j的第t個元素。

③針對任一場景wi，通過比較與其匹配的場景對的距離大小，找到最靠近場景wi的場景，根據場景縮減原則進行刪除，將被刪除的場景概率累加到距離最近的場景上；④重復進行步驟③，直到刪除場景的數量達到K結束；⑤最終得到縮減后的風電出力場景和負荷場景以及對應的場景概率。

2 基于可靠性指標的備用量化模型

根據建立的場景集，系統可靠性由失電量期望（Expected Energy NotSupplied，EENS）與棄風電量 期 望 （Expected Wind Curtailment Quantity，EWCQ）表示。基于可靠性指標，綜合考慮電力系統不確定因素，推導系統備用需求與可靠性指標之間的量化關系[15]。

2.1 失電量期望

t時刻，場景k下，如果系統提供的備用容量小于功率缺額時，則需要的切負荷量為

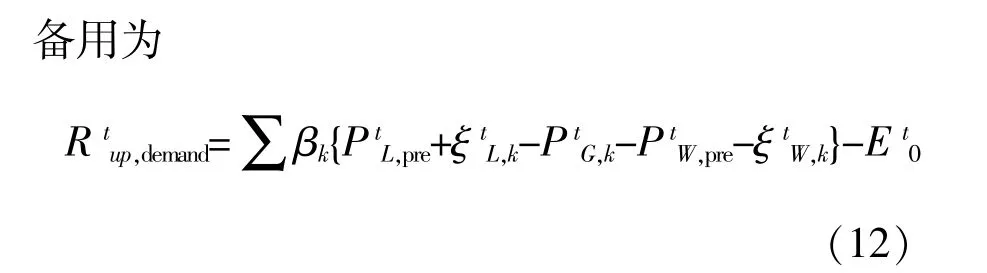
2.2 棄風電量期望

風電出力具有反調峰特性，在夜間負荷低谷，風電大發會造成大量棄風損失。根據上述場景集，場景k下t時刻可能出現的棄風電量為[16]

式中：Rtdn，k為t時刻系統所需最小下調備用。

3 發電與備用協調優化模型

本文將系統備用容量需求分為上調備用和下調備用，上調備用了解決負荷缺額的情況，下調備用解決了風電出力過大的問題。將備用與發電進行協調調度，在制定機組啟停和出力計劃的同時，可以確定系統備用計劃，故該模型可以同時得到系統的機組發電計劃，備用調度和每個時刻的系統最小備用需求。基于場景集，建立兼顧系統可靠性和經濟性的動態協調優化模型。

3.1 目標函數

預留備用過高造成經濟浪費，預留備用過低，可靠性難以滿足。為了實現電力系統可靠性和經濟性最優折中，本文發電與備用協調調度優化模型的目標有3個層面[17]：①最小機組運行成本；②最小機組啟停成本；③最小預留備用成本，其表達式為

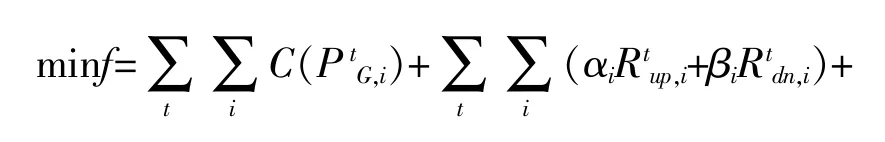
3.2 約束條件

本文約束條件包括功率平衡約束，機組出力約束，爬坡約束，機組啟停時間約束，均引用文獻[10]，在此不做贅述。另外本文計入潮流安全約束和可靠性約束。

①潮流安全約束

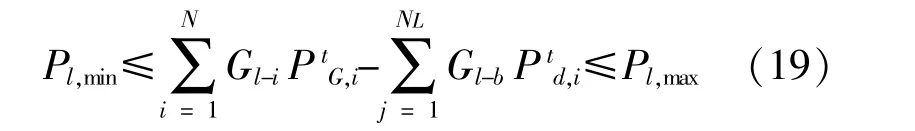
式中：NL為負荷節點數量；Ptd，i為節點d在t時刻的負荷需求；Gl-i為機組i出力對線路l的功率轉移因子；Gl-b為節點負荷b對線路l的轉移因子；Pl，min，Pl，max分別為線路l傳輸有功的下限和上限。

②可靠性約束

4 模型求解與算例分析

4.1 參數設置

本文以IEEE-30節點系統為基礎進行仿真分析，系統包含6臺發電機和一個風電場，其中發電機總裝機容量為1 900MW，最大機組容量是500MW，具體特性參數見文獻[18]。風電場總裝機容量為600MW。風電預測曲線按照風電場最大裝機容量進行標幺化，設置每小時最小棄風電量為風電預測值的0.5%。系統最大負荷為1 450 MW，負荷預測曲線按照最大負荷進行標幺化，其曲線如圖1所示。

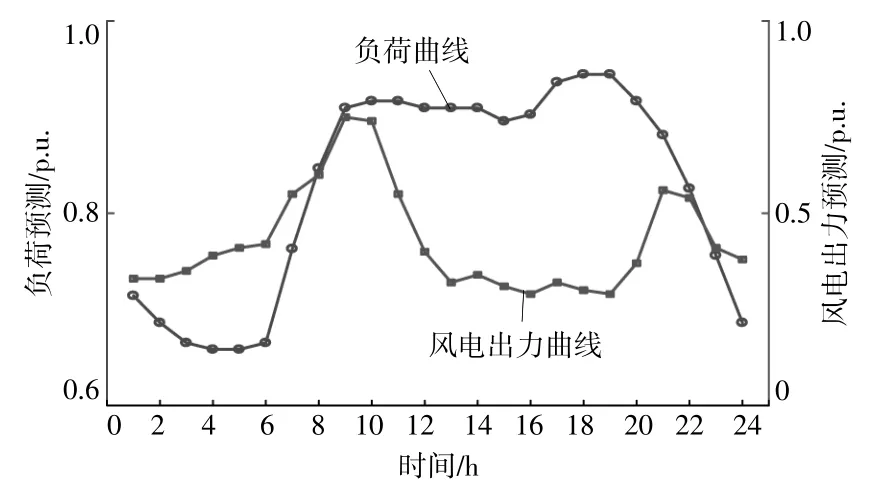
圖1 24 h風電出力和負荷預測數據Fig.1 Predicted data ofwind power and load on 24 hours

設置每小時最大切負荷電量為負荷預測值的0.1%。設系統單位備用成本為30美元/MW，切負荷單位成本為10 000美元/MW，棄風單位成本為10 000美元/MW[19]。

4.2 場景生成與縮減

本文采用LHS方法分別得到500個風電出力初始場景和負荷初始場景，如圖2所示。得到的初始場景變化趨勢大體相同，每個時段的出力在一定的置信區間內出現相應的偏差。

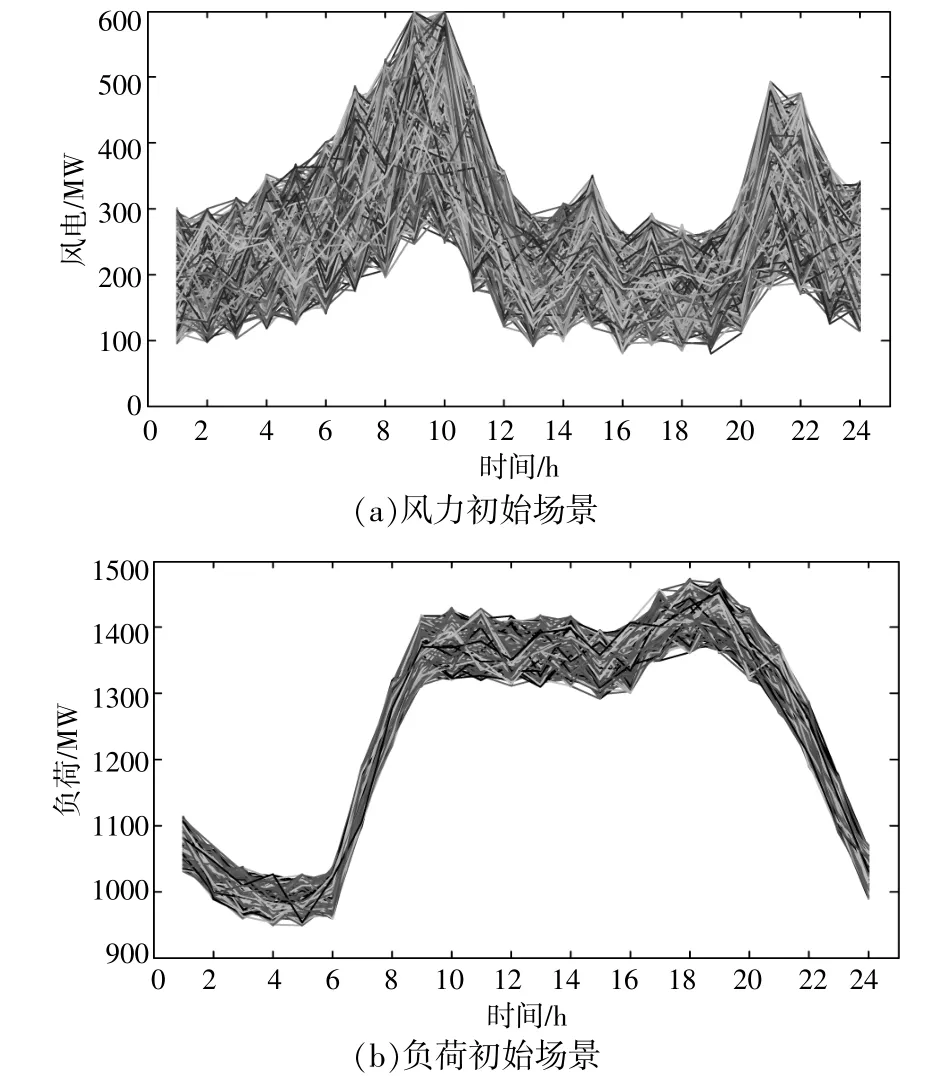
圖2 拉丁超立方模擬得到的風電出力場景和負荷場景Fig.2 The wind power scenarios and the load scenarios based on LHSmethod

經過同步回代縮減后得到5條風電出力曲線和2條負荷預測曲線，如圖3所示。由于風電出力預測方差遠大于負荷預測誤差方差，因此風電出力場景更加發散，而負荷場景較為集中。

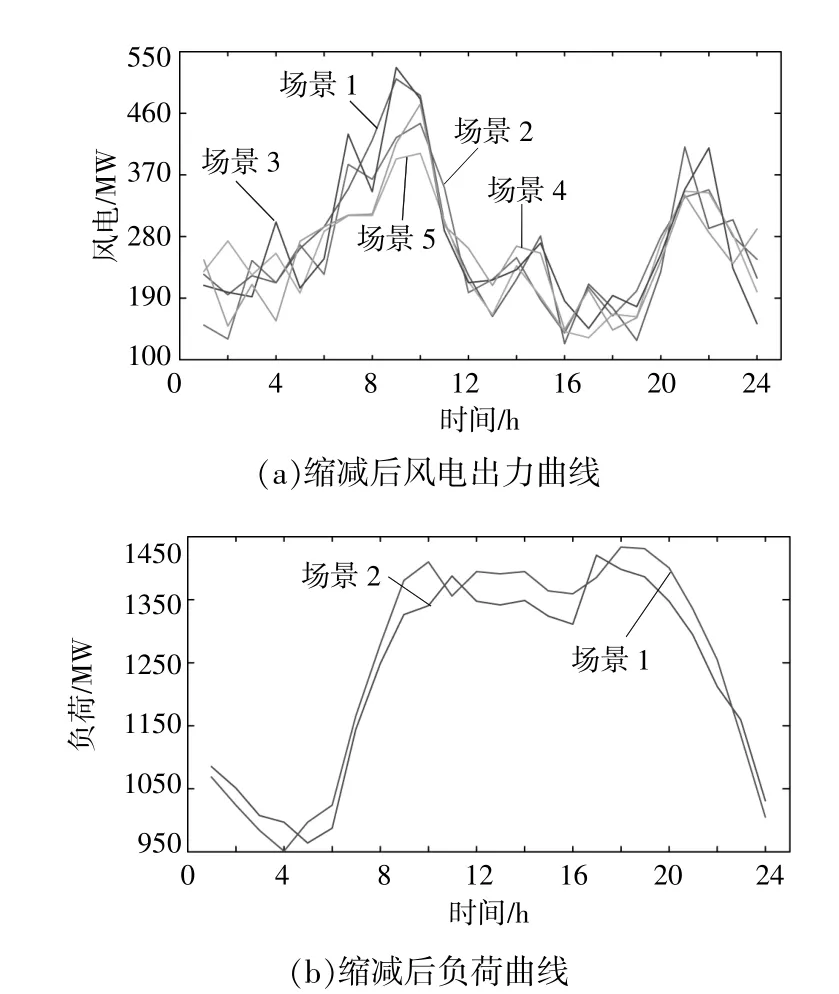
圖3 縮減后的風電出力場景和負荷場景Fig.3 The wind power scenarios and the load scenarios reduced

縮減場景后，對應的場景概率如表1所示。

表1 縮減后風電出力場景和負荷場景對應概率Table 1 The probability of the wind power output scenarios and load scenarios reduced

4.3 不同備用決策方案對比分析

為驗證本文模型的正確性，本文選取3種不同備用決策方案進行對比分析。方案1為本文提出的運行備用方案；方案2為確定性備用方案，運行備用為PtL，pre×10%+PtW，pre×15%；方案3為傳統確定性備用方案，運行備用為PtL，pre×15%。

本文方法量化得到的備用需求結果與兩種確定性方法得到的結果進行比較，如圖4所示。

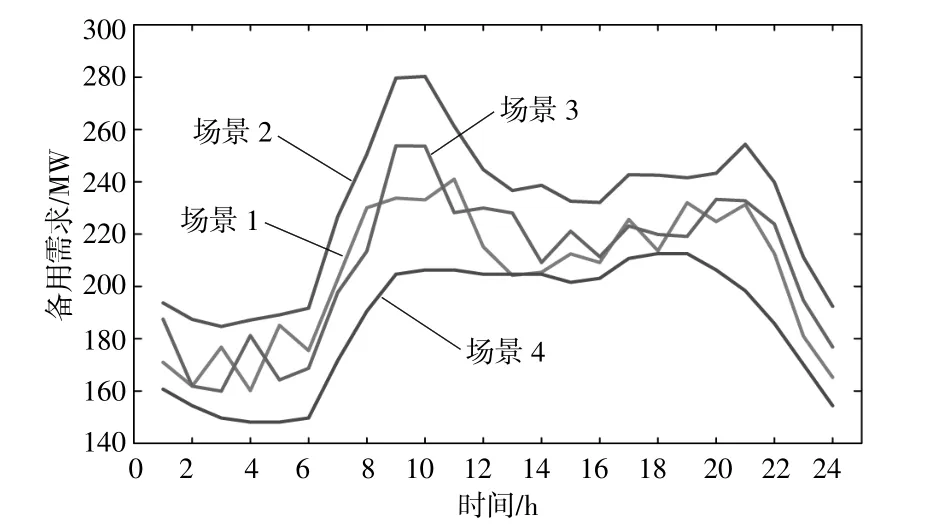
圖4 不同方案下系統備用需求對比圖Fig.4 Comparison of system reserve requirementunder different schemes

由于負荷預測精度高于風電出力預測，風電預測誤差成為電力系統不確定性主要原因。方案3只考慮負荷不確定性，忽略風電波動對備用需求的影響，其結果均低于其他方案的備用需求，難以滿足可靠性要求，造成巨大的棄風和切負荷懲罰。方案2考慮了負荷和風電預測誤差，但其結果隨著負荷和風電百分比的變化而變化，其靈活性較差，不能實現全局最優。本文方案在保證可靠性的前提下，減少了備用需求，實現了電力系統可靠性與經濟性最優折中，具有很強的實用性。

分別計算不同方案下的系統運行成本，系統運行成本包括機組運行成本，啟停成本，可用備用成本和棄風切負荷懲罰期望，其結果如表2所示。

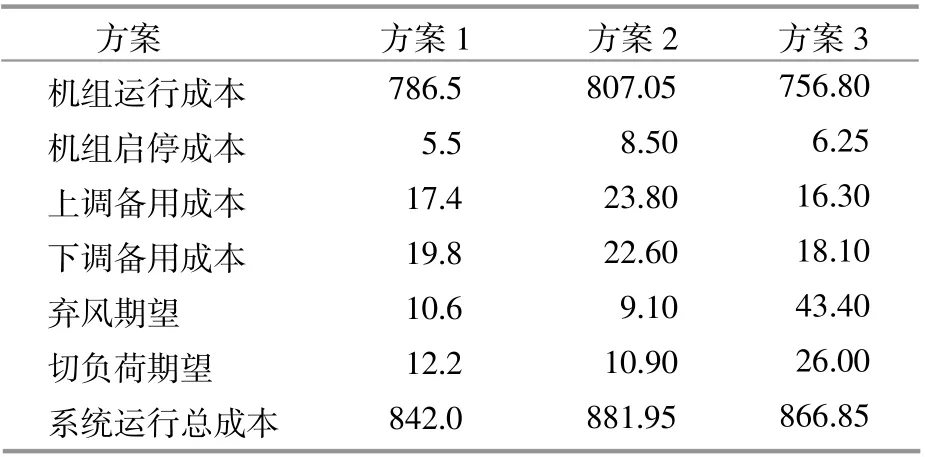
表2 不同方案下優化結果對比Table 2 Comparison of optimization results under different schemes 104美元

方案2的機組運行成本最高，由于備用需求高于其他方案，所以不得不需要更多的機組提供備用，這樣上調備用成本和下調備用成本高于其他方案，增加了系統運行成本。雖然棄風懲罰期望和切負荷懲罰期望最低，但是經濟性難以達到最優。方案3備用需求較低，且機組運行成本最低，但其棄風懲罰期望和切負荷懲罰期望均高于其他方案，高額的棄風和切負荷懲罰使得系統可靠性難以得到保證，不具有實用性。本文方案可以更好的量化風電，負荷不確定性與備用需求的關系，能夠以較少的備用容量成本使電網更可靠地運行，實現經濟性和可靠性的統一。

采用本文方案后機組啟停次數如圖5所示。由圖5可知，本文在滿足供電可靠性和減少棄風的基礎上，優化了機組組合方案，避免機組頻繁啟停，實現機組啟停成本的降低。在柱狀圖中，1號機組和4號機組主要承擔平衡系統負荷的任務，同時提供少量的旋轉備用容量，2號機組和3號機組主要用來承擔提供旋轉備用的任務。

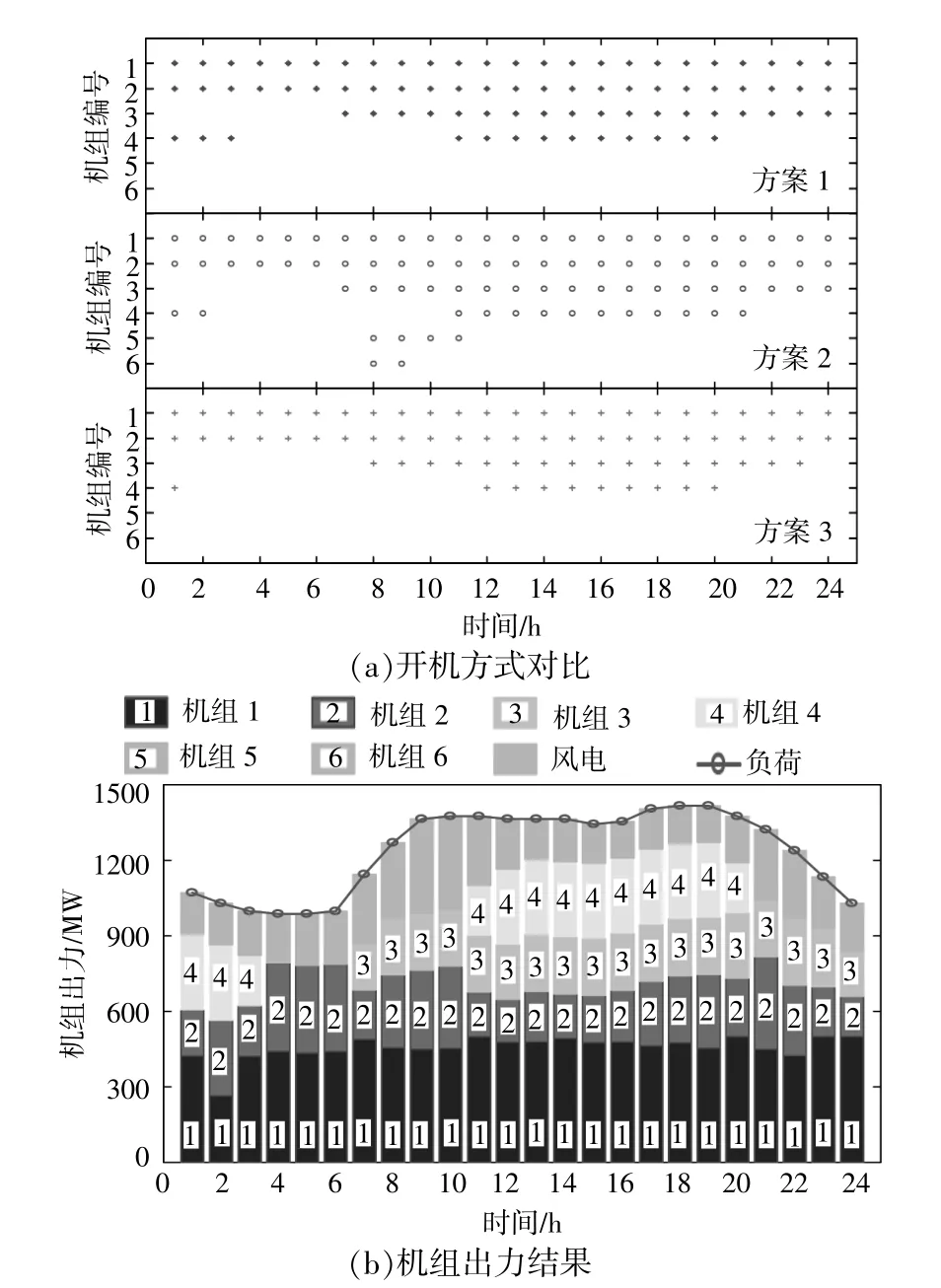
圖5 不同方案開機方式對比和機組出力結果Fig.5 Comparison of unit commitmentunder different schemes and optimization resultof unit output

圖6為各時段系統備用需求與供給的結果。

圖6 24 h備用需求與可用備用容量對比Fig.6 Comparison of reserve requirementand available reserve on 24 hours

由圖6可以看出，在任何時段，機組的備用供給容量均能滿足備用需求，較高的備用供給可以提高系統可靠性，但備用容量過多會造成浪費，出現“備而不用”的不經濟現象。

根據發電機參數特征，6臺發電機單位備用成本分別取40，40，30，30，50，50美元/MW，并在目標函數中加入備用成本約束，使其在滿足每小時備用容量需求時，進一步減少發電機旋轉備用，實現經濟性最優。備用容量結果如圖7所示。

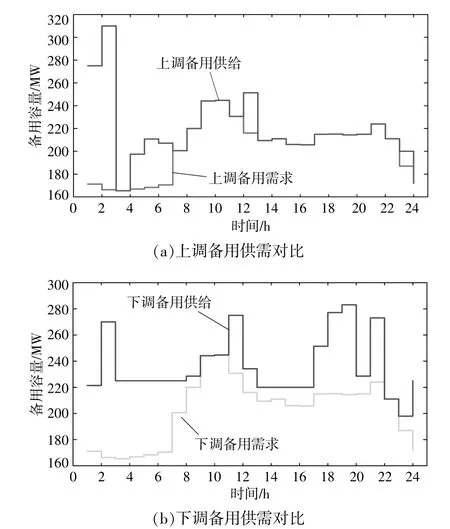
圖7 考慮備用成本后24 h備用需求與可用備用容量對比Fig.7 Comparison of reserve requirementand available reserve after considering reserve coston 24 hours

與圖6對比可以看出，在沒有加入備用成本約束之前，雖然每個時段預留的運行備用可以滿足該時段的備用需求，但是遠高于備用需求，造成了極大的備用浪費，這也是難以滿足經濟性要求的原因。在計入備用成本約束后，減少了系統每小時可用備用容量，從而實現經濟性與可靠性的最優折中。

4.4 不同滲透率下運行備用優化結果

本文模型通過增加風電機組數量來改變風電滲透率，在不改變常規機組裝機容量的條件下，風電滲透率隨風電裝機容量的變化而變化。圖8給出了本文方案在不同風電滲透率情況下的運行備用優化結果。

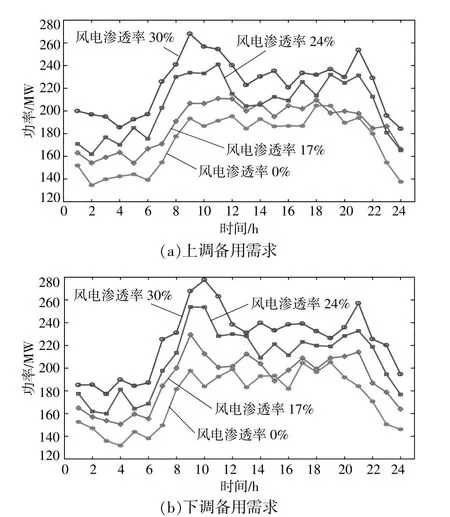
圖8 不同風電滲透率下備用需求結果Fig.8 Reserve requirement under differentwind penetration

在火電機組裝機容量不變的條件下，隨著風電滲透率增加，運行備用需求呈現增長趨勢。結合風電與負荷預測曲線可以看出：上調備用和下調備用增長趨勢相似，在風電大發期間，運行備用需求增長較大；在風電出力較小的時刻，需求增長比較平緩。本文方案可以根據風電滲透率水平，適當調整運行備用需求，對制定火電機組日前出力調度計劃具有一定指導意義。

5 結束語

針對大規模風電并網帶來的電力系統機組出力和備用決策的調度問題，本文基于場景法得到風電與負荷場景，綜合考慮電網運行約束，對電力系統可靠性與失電量期望指標和棄風電量期望指標進行量化分析；建立機組運行成本最小，預留備用成本最低的機組出力和運行備用的協調調度模型。算例證明，本文方法得到的運行備用需求能滿足每小時可靠性要求，為接納可再生能源提供更大空間。另外，本文方案可以優化機組啟停和出力計劃，減少每個時段的可用備用容量，避免備用過剩的問題，實現經濟性與可靠性兩者最優。