基于特征分裂有限元準(zhǔn)隱格式的共軛傳熱整體耦合數(shù)值模擬方法1)

劉 瑜 鄧家鈺 王成恩,2) 蘇紅星

?(上海交通大學(xué)機(jī)械與動(dòng)力工程學(xué)院,上海 200240)

?(大連理工大學(xué)航空航天學(xué)院,遼寧大連 116024)

引言

共軛傳熱現(xiàn)象在科學(xué)和工程領(lǐng)域中大量存在[1],比如核反應(yīng)系統(tǒng)[2],燃?xì)廨啓C(jī)渦輪葉片冷卻[3-4],航天器熱防護(hù)[5-6],化工處理[7],生物醫(yī)學(xué)[8-9],電子設(shè)備散熱[10],MEMS 設(shè)備中的微槽道對(duì)流換熱[11]等.

共軛傳熱問(wèn)題除了實(shí)驗(yàn)研究以外,可以通過(guò)理論分析或數(shù)值模擬的方法求解.理論分析方法對(duì)簡(jiǎn)單的模型(如平板,圓管等)進(jìn)行建模,通過(guò)簡(jiǎn)化得到精確或近似的理論解[12].理論方法對(duì)共軛傳熱問(wèn)題的理解很重要,但只適用于簡(jiǎn)單的問(wèn)題.數(shù)值模擬將流動(dòng)的數(shù)值解與固體傳熱的數(shù)值解耦合起來(lái),主要有兩種耦合方法:分區(qū)耦合(partitioned)[13]和整體耦合(monolithic)[14]方法.分區(qū)耦合方法對(duì)流場(chǎng)和固體熱分析采用各自相應(yīng)的成熟的求解器,然后通過(guò)迭代方法滿足流熱耦合的界面條件,即在界面上溫度和熱流應(yīng)是連續(xù)的.分區(qū)耦合方法的優(yōu)點(diǎn)是可以采用現(xiàn)有的流動(dòng)和固體熱分析求解程序,但是為了滿足界面條件需要進(jìn)行迭代求解,在不同的求解器之間傳遞邊界條件,算法實(shí)現(xiàn)復(fù)雜,并且還需要考慮分區(qū)耦合算法在流固耦合界面上的穩(wěn)定性條件[15-20].整體耦合方法將流動(dòng)方程和固體傳熱方程統(tǒng)一離散,然后求解單一的方程.整體耦合方法的優(yōu)點(diǎn)是不需要處理流固耦合界面條件,缺點(diǎn)是如果流動(dòng)特征時(shí)間和固體傳熱特征時(shí)間差別很大,非定常共軛傳熱的計(jì)算量將是巨大的[21-22].

目前存在大量的數(shù)值方法模擬共軛傳熱問(wèn)題，如有限差分法[23],有限體積法[6,24-25],浸入式邊界法[26],無(wú)網(wǎng)格法[27],格子玻爾茲曼方法[28-30],邊界元法[31],有限元法等.有限元法在計(jì)算固體傳熱問(wèn)題上具有優(yōu)勢(shì)，如果流場(chǎng)求解也采用有限元求解,可以降低程序?qū)崿F(xiàn)的復(fù)雜性.采用有限元法求解共軛傳熱的文獻(xiàn)相對(duì)較少.Misa 和Sarkar[32]采用整體耦合方法,利用滿足inf-sup 條件的經(jīng)典伽遼金(Galerkin)有限元方法對(duì)方腔自然對(duì)流的共軛傳熱進(jìn)行了模擬.Malatip 等[33]采用Rice 和Schnipke[34]提出的交錯(cuò)有限元方法和整體耦合方法求解定常共軛傳熱問(wèn)題.Malatip 等將Choi 和Yoo[35]提出的二階時(shí)間精度分裂有限元方法推廣到求解共軛傳熱問(wèn)題[36]和流?熱?結(jié)構(gòu)耦合問(wèn)題[37].Verstraete 和Scholl[19]以及Scholl 等[20]采用壓力穩(wěn)定有限元法計(jì)算流動(dòng),定常有限元法計(jì)算固體傳熱,對(duì)分區(qū)耦合方法計(jì)算定常共軛傳熱的穩(wěn)定性問(wèn)題進(jìn)行了研究.Long 等[38]將光滑有限元方法(smoothed finite element method) 和改進(jìn)的光滑粒子流體動(dòng)力學(xué)方法耦合起來(lái)求解熱?流?結(jié)構(gòu)相互作用問(wèn)題.

利用伽遼金有限元法求解不可壓縮流動(dòng),需要有限單元滿足所謂的inf-sup 條件,即速度和壓力的插值函數(shù)不能具有相同的階數(shù)[39].這增加了算法實(shí)現(xiàn)的難度,特別是對(duì)于三維問(wèn)題更是如此.為了采用等階元計(jì)算,Hughes 等[40]提出了用PSPG (Pressure-Stabilizing/Petrov-Galerkin) 穩(wěn)定項(xiàng)來(lái)規(guī)避inf-sup 條件,為了實(shí)現(xiàn)對(duì)流主導(dǎo)流動(dòng)的穩(wěn)定計(jì)算還需要添加SUPG(Streamline-Upwind/Petrov-Galerkin) 穩(wěn)定項(xiàng)[41].Zienkiewicz 等[42]在分?jǐn)?shù)步法的基礎(chǔ)上,提出了基于特征分裂的有限元法(CBS).CBS 方法有半隱格式(semi-implicit),準(zhǔn)隱格式(quasi-implicit) 和基于人工壓縮性的格式(CBS-AC)[42].準(zhǔn)隱格式的時(shí)間步長(zhǎng)只取決于對(duì)流穩(wěn)定性,計(jì)算效率高于半隱格式和基于人工壓縮性的格式[43].在作者閱讀的有限文獻(xiàn)范圍內(nèi),還沒(méi)有看到將CBS 方法的準(zhǔn)隱格式用于共軛傳熱數(shù)值模擬的例子.CBS 方法既適用于不可壓縮流動(dòng)的求解,也適用于亞聲速、超聲速流動(dòng)的求解;并且同樣可以采用等階插值函數(shù);CBS 方法是分?jǐn)?shù)步方法,每一個(gè)分裂步得到的方程是標(biāo)量方程,對(duì)存儲(chǔ)量要求小,方程的求解也相對(duì)容易.本文的主要目的是采用CBS 方法的準(zhǔn)隱格式,發(fā)展一種整體耦合層流共軛傳熱數(shù)值模擬方法.

本文接下來(lái)給出共軛傳熱的控制方程,并介紹流場(chǎng)計(jì)算采用的基于特征分裂的有限元方法,隨后給出整體耦合共軛傳熱數(shù)值模擬算法.為了驗(yàn)證本文所采用算法的準(zhǔn)確性,對(duì)不可壓縮流動(dòng)問(wèn)題和共軛傳熱問(wèn)題進(jìn)行了模擬.

1 計(jì)算方法

1.1 控制方程

非守恒形式的不可壓縮Navier-Stokes 方程為

上式是無(wú)量綱化的方程,其中ui,(i=1,2,3)是流體速度分量,p是流體靜壓,Re為雷諾數(shù).方程中變量下標(biāo)滿足愛(ài)因斯坦求和規(guī)則.

假設(shè)流體的密度是常量,且其他流體性質(zhì)也與溫度無(wú)關(guān).將能量方程表示為溫度的形式,即

其中,T為溫度,Qf為流體中的熱源項(xiàng),Pr為普朗特?cái)?shù).在這種情形下,能量方程與連續(xù)性方程和動(dòng)量方程解耦.溫度只是簡(jiǎn)單的輸運(yùn)變量,在得到了速度場(chǎng)后,計(jì)算溫度方程就可以得到溫度場(chǎng)的分布.

固體傳熱方程為

其中κsf=κs/κf,cr=ρscps/ρfcpf.ρf,ρs分別是流體和固體的密度,κf,κs分別是流體和固體的導(dǎo)熱系數(shù),cps和cpf分別表示固體和流體的比熱.推導(dǎo)以上無(wú)量綱方程采用的參考量見(jiàn)附錄.

1.2 求解不可壓縮流動(dòng)的分?jǐn)?shù)步法

方程(1)的半離散形式為

其中?t是時(shí)間步長(zhǎng),θ1,θ2和θ3分別是控制對(duì)流項(xiàng)、壓力項(xiàng)和黏性項(xiàng)時(shí)間離散的參數(shù),其取值范圍為[0,1].為了避免求解非線性方程,只考慮θ1=0 的情形.在推導(dǎo)CBS 格式之前,首先引入輔助變量?u?和?u??,且令

采用基于Helmholtz-Hodge 分解的2 級(jí)分?jǐn)?shù)步方法,將方程分裂為

1.3 對(duì)流穩(wěn)定項(xiàng)

對(duì)于對(duì)流占優(yōu)問(wèn)題,CBS 格式需要添加對(duì)流穩(wěn)定項(xiàng)[43].本文在半離散方程(5) 中添加顯式的穩(wěn)定項(xiàng),即

其中?ts為對(duì)流穩(wěn)定項(xiàng)需要的時(shí)間步長(zhǎng),可以認(rèn)為是穩(wěn)定性參數(shù),與SUPG 中的穩(wěn)定參數(shù)τ[41]的作用相似.在分?jǐn)?shù)步方法中,穩(wěn)定項(xiàng)也要進(jìn)行分裂,在預(yù)測(cè)步式(7)中添加的穩(wěn)定項(xiàng)為

即不考慮壓力項(xiàng).在修正步式(8) 中,穩(wěn)定項(xiàng)僅包含壓力項(xiàng),即

類似可以得到帶穩(wěn)定項(xiàng)的能量方程半離散形式,即

其中最后一項(xiàng)是對(duì)流穩(wěn)定項(xiàng).

1.4 基于特征分裂有限元方法的矩陣形式

對(duì)半離散方程采用伽遼金有限元方法進(jìn)行空間離散,根據(jù)參數(shù)的不同,可以得到不同的格式[43].

1.4.1 半隱格式

步驟1

其中Mu,i,C,K分別表示速度質(zhì)量矩陣,離散對(duì)流算子和黏性算子.Fi表示黏性邊界積分,fs,i是穩(wěn)定項(xiàng).

步驟2

步驟3

其中L,D,G分別表示離散拉普拉斯算子,離散散度算子和離散梯度算子,fp,i是穩(wěn)定項(xiàng).半隱格式是條件穩(wěn)定的,穩(wěn)定性由對(duì)流項(xiàng)和黏性項(xiàng)確定.

在計(jì)算得到了速度場(chǎng)后,即可以將速度場(chǎng)代入到能量方程計(jì)算溫度場(chǎng).

步驟4

其中,MT,KT分別是溫度方程質(zhì)量矩陣和溫度擴(kuò)散算子,FT表示溫度擴(kuò)散項(xiàng)邊界積分,QT為熱源項(xiàng),fT為穩(wěn)定項(xiàng).

半隱格式的單元穩(wěn)定時(shí)間步長(zhǎng)為

其中上標(biāo)e表示單元,h是單元的網(wǎng)格尺度,?tcon,?tvis分別是對(duì)流時(shí)間步長(zhǎng)和黏性時(shí)間步長(zhǎng).全局時(shí)間步長(zhǎng)取所有單元穩(wěn)定時(shí)間步長(zhǎng)的最小值,即

黏性穩(wěn)定性在一定條件下會(huì)對(duì)時(shí)間步長(zhǎng)產(chǎn)生嚴(yán)重的限制.為了克服這一缺點(diǎn),提出了準(zhǔn)隱格式.

1.4.2 準(zhǔn)隱格式

與半隱格式不同,準(zhǔn)隱格式對(duì)黏性項(xiàng)進(jìn)行隱式處理[43],即1/2θ31.

步驟1

黏性項(xiàng)的邊界積分仍然作顯式處理.步驟2 和步驟3與半隱格式相同.

步驟3 還可以采用非投影形式,即對(duì)于速度修正步

步驟4

準(zhǔn)隱格式的時(shí)間步長(zhǎng)只受對(duì)流項(xiàng)限制,即

以上矩陣和源項(xiàng)的具體形式見(jiàn)附錄.

說(shuō)明1:半隱格式的時(shí)間步長(zhǎng)受黏性穩(wěn)定性條件影響;而基于人工可壓縮性的格式(CBS-AC),根據(jù)文獻(xiàn)[43]報(bào)道,準(zhǔn)隱格式的計(jì)算效率比其高3 ～100 倍.因此本文計(jì)算采用準(zhǔn)隱格式.

說(shuō)明2:CBS 方法允許等階插值.本文選擇等階有限元,即速度、壓力、溫度都采用相同的有限元基函數(shù),這大大方便了程序的實(shí)現(xiàn).

說(shuō)明3:準(zhǔn)隱格式求解的四步方程的矩陣是對(duì)稱正定的,故可以采用共軛梯度法求解.預(yù)處理矩陣本文采用雅克比方法計(jì)算.

說(shuō)明4:本文計(jì)算所采用的參數(shù)為θ1=0,θ2=θ3=θ4=1.

1.5 共軛傳熱耦合算法

在進(jìn)行流固耦合模擬時(shí),需要?jiǎng)澐至鲌?chǎng)網(wǎng)格和固體網(wǎng)格.本文設(shè)計(jì)了一種流固耦合網(wǎng)格和邊界條件表達(dá)方式.出于簡(jiǎn)單考慮,流固耦合界面是適配的,即在流固耦合界面上流場(chǎng)網(wǎng)格點(diǎn)和固體網(wǎng)格點(diǎn)是一致的.為了方便,流體區(qū)域和固體區(qū)域作為一個(gè)統(tǒng)一的計(jì)算域劃分單一的網(wǎng)格.為了區(qū)分流體和固體網(wǎng)格,需要用一個(gè)指標(biāo)集來(lái)表示網(wǎng)格單元的材料屬性,考慮用一個(gè)材料屬性文件來(lái)存儲(chǔ)網(wǎng)格單元的屬性,即mateiral.txt.

對(duì)于溫度場(chǎng)而言,流固耦合邊界屬于內(nèi)面,因此在流固耦合邊界上只需要指定流場(chǎng)變量邊界條件.而在固體的其他邊界上只需要指定溫度邊界條件,不需要指定流場(chǎng)變量的邊界條件.

如果采用前面提及的流固耦合網(wǎng)格及邊界條件,可以得到共軛傳熱耦合算法如Algorithm 1 所示.

固體傳熱方程離散后的形式為

溫度方程在流體區(qū)域按照式(27) 離散,在固體區(qū)域按照式(29) 離散,最后將溫度方程裝配為統(tǒng)一的方程組.

該算法是一種整體耦合算法,與分區(qū)算法相比,不需要通過(guò)迭代就可以隱式滿足流熱耦合界面條件.

1.6 時(shí)間步長(zhǎng)

1.6.1 流體時(shí)間步長(zhǎng)

Bevan 等[43]研究了CBS 方法中的半隱格式、準(zhǔn)隱格式和基于人工壓縮性的格式的計(jì)算效率,發(fā)現(xiàn)準(zhǔn)隱格式由于只需要考慮對(duì)流時(shí)間步長(zhǎng),相比于其他兩種格式具有較高的計(jì)算效率.文獻(xiàn)[43] 中沒(méi)有對(duì)時(shí)間推進(jìn)步長(zhǎng)和穩(wěn)定項(xiàng)中的時(shí)間步長(zhǎng)進(jìn)行區(qū)分,在穩(wěn)定項(xiàng)中采用的也是時(shí)間推進(jìn)步長(zhǎng),即?ts=?t,并且建議采用半隱格式和準(zhǔn)隱格式時(shí),時(shí)間步長(zhǎng)應(yīng)該選擇全局時(shí)間步長(zhǎng).

作者認(rèn)為穩(wěn)定項(xiàng)中的時(shí)間步長(zhǎng)?ts可以視為穩(wěn)定性參數(shù),而穩(wěn)定性參數(shù)應(yīng)具有當(dāng)?shù)匦再|(zhì).當(dāng)計(jì)算采用全局時(shí)間步長(zhǎng)時(shí),如果整個(gè)計(jì)算區(qū)域的穩(wěn)定性時(shí)間步長(zhǎng)都取同樣的值,有可能不能較好地抑制數(shù)值不穩(wěn)定性.因此本文采用準(zhǔn)隱方法進(jìn)行計(jì)算,對(duì)物理推進(jìn)時(shí)間步長(zhǎng)和穩(wěn)定項(xiàng)中的時(shí)間步長(zhǎng)做了區(qū)分.物理推進(jìn)時(shí)間步長(zhǎng)?t按式(28)計(jì)算，取全場(chǎng)的最小時(shí)間步長(zhǎng)作為全局時(shí)間步長(zhǎng).穩(wěn)定項(xiàng)中的時(shí)間步長(zhǎng)為局部時(shí)間步長(zhǎng)?ts，按照式(22)計(jì)算.

1.6.2 固體時(shí)間步長(zhǎng)

在固體傳熱方程(4)中,固體密度與比熱的乘積與流體密度與比熱的乘積之比,cr,在一般情況下有cr?1.這導(dǎo)致傳熱方程時(shí)間尺度遠(yuǎn)大于流動(dòng)方程的時(shí)間尺度.He 等[44]估計(jì)了典型共軛傳熱問(wèn)題的固體和流體的穩(wěn)定時(shí)間步長(zhǎng)之比為103～105.當(dāng)對(duì)共軛傳熱問(wèn)題的流體溫度方程和固體溫度方程統(tǒng)一求解時(shí),如果采用流體部分的穩(wěn)定時(shí)間步長(zhǎng)進(jìn)行計(jì)算,則固體部分的溫度場(chǎng)需要迭代很多步才能收斂.對(duì)于定常問(wèn)題,為了提高收斂速度,在固體部分需要采用比流體時(shí)間步長(zhǎng)更大的時(shí)間步長(zhǎng)

其中?tflu和?tsol分別表示流動(dòng)計(jì)算和固體傳熱計(jì)算采用的時(shí)間步長(zhǎng),n為放大因子.

式(30)中如果選擇n=cr,則相當(dāng)于在方程(4)中令cr=1,?t=?tflu=?tsol.這是文獻(xiàn)[23,45]采用的做法.本文定義名義上的cr值為cr′,即

計(jì)算時(shí)用cr′代替cr.名義上固體時(shí)間步長(zhǎng)與流體時(shí)間步長(zhǎng)相同,但是通過(guò)調(diào)整cr′實(shí)際上改變了固體時(shí)間步長(zhǎng).cr′可以足夠小,在滿足穩(wěn)定性的前提下提高收斂速度.這將在下面的算例中得到驗(yàn)證.

2 算法驗(yàn)證

2.1 穩(wěn)定項(xiàng)時(shí)間步長(zhǎng)選取方法對(duì)計(jì)算結(jié)果的影響

首先對(duì)穩(wěn)定項(xiàng)中的時(shí)間步長(zhǎng)的選擇方式對(duì)計(jì)算結(jié)果的影響進(jìn)行比較.采用3 種方式計(jì)算穩(wěn)定項(xiàng)中的時(shí)間步長(zhǎng),分別是:與全局時(shí)間步長(zhǎng)相同,采用局部時(shí)間步長(zhǎng)和取零值(即不添加穩(wěn)定項(xiàng)).計(jì)算采用的例子是方腔頂蓋驅(qū)動(dòng)流.方腔的頂蓋按指定的速度運(yùn)動(dòng),方腔的其他邊界固定.在頂蓋的作用下,方腔中流體將發(fā)生運(yùn)動(dòng).計(jì)算域? 為(0,1)×(0,1),邊界條件都為Dirichlet 條件.頂蓋的運(yùn)動(dòng)速度,按照文獻(xiàn)[46],給定如下

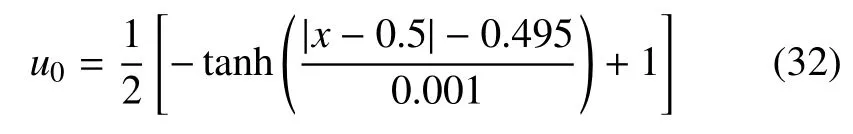
當(dāng)網(wǎng)格足夠稠密時(shí),穩(wěn)定項(xiàng)的作用不明顯,為此在這里特意選擇比較稀疏的網(wǎng)格進(jìn)行計(jì)算.網(wǎng)格包含800個(gè)線性三角形單元和441 個(gè)節(jié)點(diǎn).網(wǎng)格如圖1(a) 所示.圖1(b)～圖1(d) 分別給出了由3 種方法計(jì)算的Re=5000 時(shí)x方向上的速度分量u的云圖.圖2 給出了在y=0.8 上u的分布.可見(jiàn)如果不加入穩(wěn)定項(xiàng),流場(chǎng)變量將出現(xiàn)很大的偽振蕩;采用文獻(xiàn)[43] 中的方法,由于穩(wěn)定項(xiàng)中的時(shí)間步長(zhǎng)全場(chǎng)都是相同的,不能完全抑制偽振蕩的出現(xiàn);而采用本文的方法流場(chǎng)變量分布光滑,抑制了偽振蕩的出現(xiàn).

圖1 頂蓋驅(qū)動(dòng)流的計(jì)算網(wǎng)格和速度云圖Fig.1 Computational mesh and contours of x-component of velocity

圖2 由不同穩(wěn)定項(xiàng)計(jì)算方法得到的速度的x 分量在y=0.8 上的分布Fig.2 Velocity profile at y=0.8 predicted by different stabilization schemes

2.2 層流計(jì)算驗(yàn)證

2.2.1 方腔頂蓋驅(qū)動(dòng)流

方腔頂蓋驅(qū)動(dòng)流是用來(lái)檢驗(yàn)層流計(jì)算準(zhǔn)確性的典型算例.計(jì)算和邊界條件與上節(jié)相同.采用一階三角形單元計(jì)算,單元數(shù)為3200,節(jié)點(diǎn)數(shù)為1681,在邊界附近進(jìn)行了加密.分別對(duì)Re=400,1000,5000,10 000 時(shí)的情形進(jìn)行了計(jì)算.圖3 比較了x=0.5 上速度分量v和y=0.5 上速度分量u的分布與Ghia等[47]的計(jì)算結(jié)果,可見(jiàn)符合很好.

2.2.2 層流后臺(tái)階流動(dòng)

對(duì)于這個(gè)問(wèn)題有實(shí)驗(yàn)數(shù)據(jù)可供比較,因而為很多作者所引用.本文選擇雷諾數(shù)為229 的情形進(jìn)行計(jì)算.問(wèn)題的計(jì)算域和邊界條件如圖4 所示.進(jìn)口速度u的分布的表達(dá)式為

在壁面處按無(wú)滑移邊界條件處理,在出口速度指定Neumann 條件,壓力指定為0,在其余邊界上壓力指定為Neumann 條件.計(jì)算網(wǎng)格包含15 200 個(gè)三角形單元,7841 個(gè)節(jié)點(diǎn).

圖5 分別給出了壓力云圖和速度云圖.圖(6)給出了不同截面上速度分布與實(shí)驗(yàn)數(shù)據(jù)[48]的比較,可見(jiàn)計(jì)算結(jié)果與實(shí)驗(yàn)符合很好.

圖3 不同雷諾數(shù)條件下的速度型面Fig.3 Velocity profiles in the x and y directions

圖4 層流后臺(tái)階流動(dòng)計(jì)算域和邊界條件Fig.4 Domain and boundary conditions of flow over a backward facing step

圖5 層流后臺(tái)階流動(dòng)的壓力和速度云圖Fig.5 Pressure and velocity contours of flow over a backward facing step

2.3 共軛傳熱數(shù)值模擬

本文對(duì)若干共軛傳熱問(wèn)題進(jìn)行模擬,以檢驗(yàn)算法和程序的準(zhǔn)確性.其中,反向流動(dòng)熱交換器在模擬中考慮了cr′的取值對(duì)收斂速度的影響,其余算例都設(shè)置cr′=1.

2.3.1 共軛傳熱庫(kù)埃特流

共軛傳熱庫(kù)埃特流[33]的示意圖為圖7.上壁以固定速度運(yùn)動(dòng),溫度為T(mén)2=0;下壁固定具有厚度,需要考慮熱傳導(dǎo),下壁底部溫度為T(mén)1=1;流固耦合界面上溫度的精確解為

其中h1,h2分別為固體和流體區(qū)域的厚度.流體域中的溫度和固體域中的溫度在y方向上為線性分布.

圖8 給出了取不同的κsf值時(shí),由一階三角形單元計(jì)算的溫度沿y方向上的分布曲線,網(wǎng)格單元數(shù)為1200.可見(jiàn)計(jì)算值與理論值十分吻合.

圖8 不同條件下共軛傳熱庫(kù)埃特流溫度分布曲線與理論解的比較Fig.8 Comparison of benchmark solutions for Couette flow condition

2.3.2 二維反向流動(dòng)熱交換器

二維反向流動(dòng)熱交換器的示意圖如圖9 所示.在熱交換器中分布兩個(gè)平行流道,流道被一金屬平板分隔開(kāi).兩個(gè)流道的厚度分別為δ1,δ3,隔板的厚度為δ2.流道的外壁是絕熱的,流道入口處的速度和溫度被認(rèn)為是均勻的.計(jì)算采用的參數(shù)如下:幾何參數(shù)δ1=δ2=δ3=0.1 m,L=1 m;流動(dòng)參數(shù)U1=0.2 m/s,T1=800 K,U3=0.1 m/s,T3=300 K,ρf=1000 kg/m3,κf=10 W/(m·K),cpf=25 J/(kg·K),μ=0.15 kg(m·s);金屬板的物性ρs=8000 kg/m3,κs=50 W/(m·K),cps=500 J/(kg·K).

圖9 二維反向流動(dòng)熱交換器Fig.9 A conjugate counter flow heat exchanger

計(jì)算網(wǎng)格采用線性三角形單元,單元數(shù)為3360,節(jié)點(diǎn)數(shù)為1763.

在本例中cr的準(zhǔn)確值為160.為了考慮cr′的取值對(duì)收斂速率的影響,分別對(duì)cr′采用準(zhǔn)確值和cr′=1,0.001 的情形進(jìn)行了模擬,圖10 給出了溫度殘值的收斂曲線.可見(jiàn)cr′如果采用準(zhǔn)確的值,收斂將非常緩慢.如果令cr′=1,收斂速度將大幅增大,繼續(xù)減小cr′的值，收斂速度會(huì)繼續(xù)增大.cr′的取值不影響最終的收斂解.

圖10 采用不同的cr′ 的收斂速率比較Fig.10 Comparison of convergence rate for different cr′ values

計(jì)算的速度場(chǎng)和溫度場(chǎng)分別如圖11(a)和圖11(b)所示.本文還計(jì)算了不同的固體和流體熱傳導(dǎo)系數(shù)之比條件下的共軛傳熱.在x=L/2 上溫度的分布曲線如圖12 所示,并與Malatip 等[37]計(jì)算的結(jié)果進(jìn)行比較,可見(jiàn)與文獻(xiàn)給出的結(jié)果符合良好.

圖11 二維反向流動(dòng)熱交換器x 方向上的速度云圖和溫度云圖Fig.11 Predicted x-component of velocity and temperature contours for a counter flow heat exchanger

圖12 分別取κsf=0.1,1,5,10,二維反向流動(dòng)熱交換器的溫度在x= L/2 上的分布與文獻(xiàn)[37]的比較Fig.12 Temperature distributions at x= L/2 for κsf=0.1,1,5,10 of a counter flow heat exchanger compared with results from Ref.[37]

2.3.3 加熱固體的強(qiáng)迫對(duì)流冷卻

第3 個(gè)測(cè)試?yán)邮橇鲃?dòng)流經(jīng)兩塊平行平板間含有3 個(gè)矩形加熱固體的強(qiáng)迫對(duì)流冷卻問(wèn)題.該問(wèn)題首次由Davalath 和Bayazitoglu[23]提出用來(lái)模擬集成電路元件的冷卻.該問(wèn)題的計(jì)算域和邊界條件如圖13 所示,矩形塊尺寸相同,且等間距分布.流體以完全發(fā)展的速度型面從左側(cè)進(jìn)入,從右側(cè)流出.3 個(gè)固體塊中的生成的熱可以假設(shè)為具有均勻分布的熱源項(xiàng),本文中假設(shè)熱源項(xiàng)Qs=8.計(jì)算時(shí)取Pr=0.71,κsf=10,分別計(jì)算了雷諾數(shù)為Re=100,500,1000 的情形.計(jì)算網(wǎng)格如圖14 所示,網(wǎng)格中含有個(gè)10 900 個(gè)線性三角形單元,5708 個(gè)網(wǎng)格節(jié)點(diǎn).圖15 給出了雷諾數(shù)為100 時(shí)的壓力、速度和溫度云圖.圖16 給出了固體?流體界面上溫度的分布,并與文獻(xiàn)[37]的結(jié)果進(jìn)行了比較,可見(jiàn)本文計(jì)算結(jié)果與文獻(xiàn)符合很好.

圖13 加熱固體的強(qiáng)迫對(duì)流冷卻問(wèn)題的計(jì)算域和邊界條件Fig.13 Domain and boundary conditions of forced convection cooling across rectangular blocks

圖14 加熱固體的強(qiáng)迫對(duì)流冷卻問(wèn)題的計(jì)算網(wǎng)格Fig.14 Computational mesh of forced convection cooling across rectangular blocks

圖15 雷諾數(shù)為100 時(shí),加熱固體的強(qiáng)迫對(duì)流冷卻的壓力,速度幅度和溫度云圖Fig.15 Pressure,velocity magnitude and temperature contours for Re=100

圖16 雷諾數(shù)為100,500,1000 時(shí)固體?流體界面上溫度的分布與文獻(xiàn)[37]的比較Fig.16 Comparison of wall temperature distributions along solid-fluid interface of rectangular blocks for Re=100,500,1000 with Ref.[37]

3 結(jié)論

本文通過(guò)將物理推進(jìn)時(shí)間步長(zhǎng)與穩(wěn)定項(xiàng)中的時(shí)間步長(zhǎng)進(jìn)行區(qū)別,改進(jìn)了基于特征分裂的有限元法的準(zhǔn)隱格式,使其具有了更好的穩(wěn)定性.在此基礎(chǔ)上,利用改進(jìn)了的準(zhǔn)隱格式和整體耦合方法實(shí)現(xiàn)了不可壓縮流體和固體間共軛傳熱的數(shù)值模擬并通過(guò)與理論、實(shí)驗(yàn)和文獻(xiàn)中的數(shù)值解進(jìn)行比較,驗(yàn)證了本文提出方法的正確性.還研究了固體區(qū)域時(shí)間步長(zhǎng)對(duì)定常共軛傳熱問(wèn)題數(shù)值模擬收斂性的影響,發(fā)現(xiàn)選擇合適的固體時(shí)間步長(zhǎng)可以顯著提高收斂速率.

本文的一個(gè)不足之處是沒(méi)有對(duì)穩(wěn)定時(shí)間步長(zhǎng)對(duì)基于特征分裂的有限元法準(zhǔn)隱格式的穩(wěn)定性的影響進(jìn)行理論分析,在未來(lái)的工作中將對(duì)此進(jìn)行研究;同時(shí)還可以研究物理推進(jìn)時(shí)間步長(zhǎng)采用局部時(shí)間步長(zhǎng)對(duì)定常共軛傳熱問(wèn)題計(jì)算收斂性的影響.未來(lái)還將采用本文提出的方法對(duì)自然對(duì)流和混合對(duì)流問(wèn)題進(jìn)行研究,進(jìn)一步探索該方法的適用范圍.

附錄

控制方程的無(wú)量綱化

有量綱形式的控制方程為: