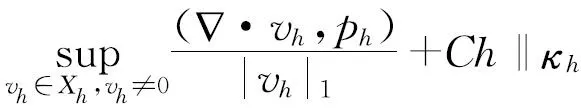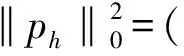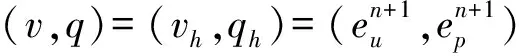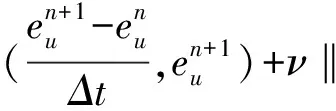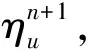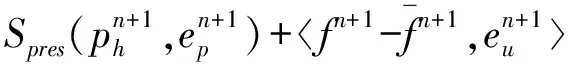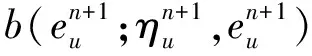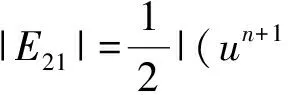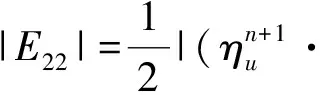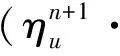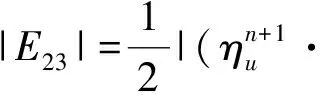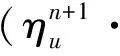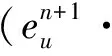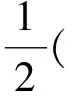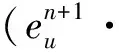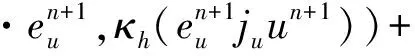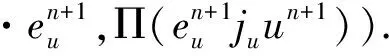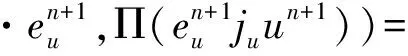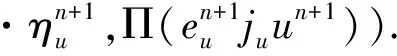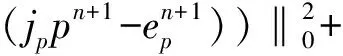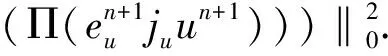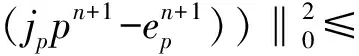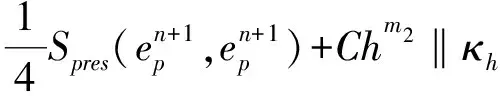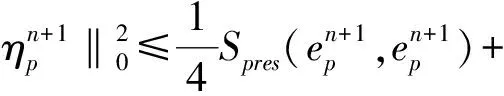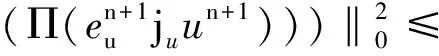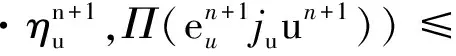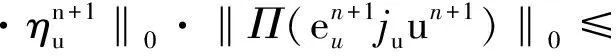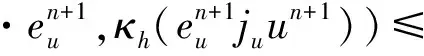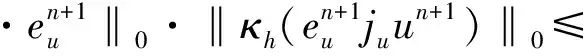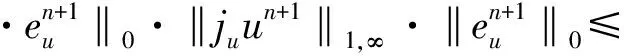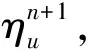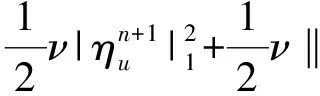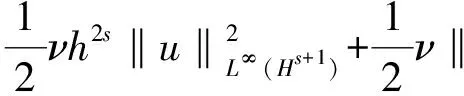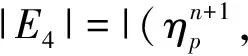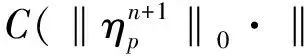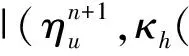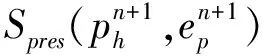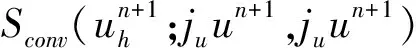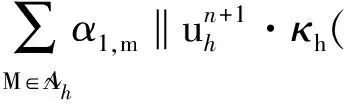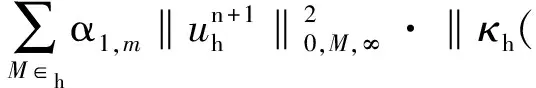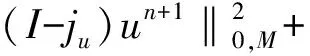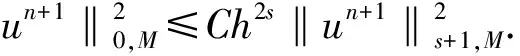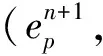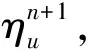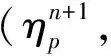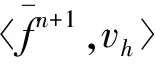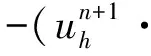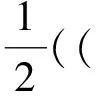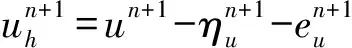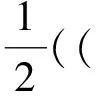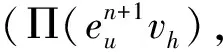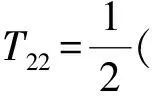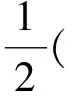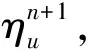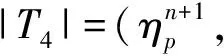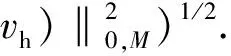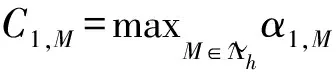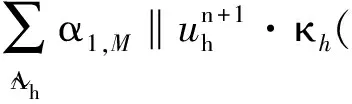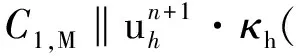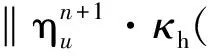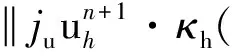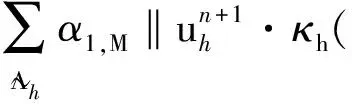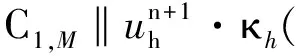非定常Navier-Stokes方程的一種非線性局部投影穩定化有限元方法

李 西， 羅加福， 馮民富

(1.四川大學數學學院, 成都 610064； 2.成都體育學院， 成都 610041)

1 引 言

粘性不可壓縮Navier-Stokes方程(NS方程)的混合有限元離散通常會出現兩個難點:需滿足經典的inf-sup條件和需要克服由高雷諾數(Reynolds number,Re)導致的數值震蕩.

為了解決上述兩個問題, 大量專家學者提出了不同的穩定化方法.比如，為了克服對流-擴散方程中對流占優時所引起的數值震蕩,Brooks和Hughes[1]提出了Streamline Upwind Petrov-Galerkin方法(SUPG),并將其推廣到不可壓縮非定常NS方程.隨后, Hughes 和Franca等[2]發現SUPG法不僅可以保持格式的相容性,不損失解的逼近性,還能增強離散解的穩定性——可利用SUPG 法避免inf-sup條件從而得到了速度和壓力的等階有限元插值.這種用來穩定離散壓力的Petrov-Galerkin變分又被稱為Pressure Stabilized Petrov-Galerkin(PSPG). 雖然SUPG/PSPG既可以做到避免inf-sup條件,又可以得到對高Re依然有效的先驗誤差估計，但需在經典的Galerkin變分格式中引入最小二乘項,導致穩定項中含有非物理耦合項,從而在用高階元近似時穩定化格式中需要計算二階導數[3-4].隨后,Becker和Braack提出的Local Projection Stabilization方法(LPS)[5]很好地解決了上述不足.與SUPG相比, LPS中添加的穩定項中不含有速度-壓力的耦合項,并且不需要計算二階導數，也可以避免inf-sup條件和克服對流占優.正因如此,LPS從提出到現在得到了充分地發展.從文獻[5]中首次采用LPS來處理Stokes問題之后，LPS被推廣到了運輸方程[6],Oseen方程的低階離散[7],NS方程[8-9]以及其它一些相關工作[10-12].

在處理由高Re帶來的數值震蕩時,Burman和Fernandez等[13]采用了Bertoluzza在文獻[14]中證明了的離散commutator性質,得到的誤差估計隨著流體Re的增大依然有效,即該數值格式可以克服由高Re帶來的數值震蕩.之后, Chen和Feng等[9]以及Frutos和Garcia等人[12,15]將上述技巧用在NS方程的LPS方法中,同樣得到了對高Re依然有效的誤差估計.

本文在文獻[9,11-12,16]基礎上,提出了一種基于非線性項的局部投影穩定格式，其中時間半隱格式中的非線性局部投影項等價于文獻[16]中的SUPG-type穩定項和文獻[11]中的高階term-by-term穩定項(因而本文提出的非線性局部投影可看做是該兩類穩定方法的非線性推廣)，對速度-壓力我們采用等階元(Pk,Pk)進行逼近,并添加局部壓力梯度投影穩定化項克服inf-sup條件.在分析離散解的先驗誤差估計時,我們采用Bertoluzza[14]提出的離散commutator性質，得到的誤差估計右端項的常系數中不含有粘性系數的倒數1/ν,使得當流體的Re增大(即流體的粘性系數ν減小)時該誤差估計依然有效.

2 半離散穩定化有限元格式

Hm(Ω)=Wm,2(Ω),

‖·‖m,M=‖·‖Hm(M),

‖·‖k,∞,M=‖·‖Wk,∞(M).

當M=Ω時，我們省略下標M,即‖·‖m=‖·‖Hm(Ω),‖·‖k,∞=‖·‖Wk,∞(Ω), 其中k=1,2是一個整數. 我們分別用Lp,Hs和Wm,p來表示相應于Lp,Hs和Wm,p的向量值Sobolev 空間,以及

設X為Sobolev空間, 定義映射φ(x,t):[0,T]→X,

并簡記‖φ‖Lp(X)=‖φ‖Lp(0,T;X),p=2或∞.

取時間區間I=[0,T], 其中T為一個固定的正常數. 非定常不可壓縮粘性流體的流動由以下非定常Navier-Stokes方程表示:

(1)

其中u=u(x,t)∈Rd,p=p(x,t)∈R,f=f(x,t)∈Rd分別表示不可壓縮粘性流體流動的速度場, 壓力場和外力場. 設特征長度L和特征速度U均為單位1. 于是該系統的運動粘度系數ν=Re-1, 其中Re為雷諾數.

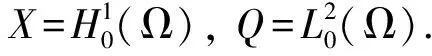
求(u,p)∈X×Q, 滿足

(?tu,v)+b(u;u,v)+ν(?u,?v)-(p,?·v)=

(2)

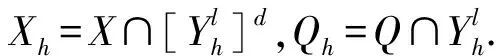
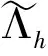
Xh(M)={vh|M:vh∈Vh,vh=0 on ΩM}.

由文獻[17], LPS方法誤差分析的關鍵在于存在一個插值算子j滿足如下最優近似性質:

假設2.1令以下局部inf-sup條件成立：

β>0

(3)

由該局部inf-sup條件可以推導出插值算子ju和jp具有如下的正交性和近似性[17]:

引理2.2令假設2.1成立.則存在兩個插值算子ju:X→Xh,jp:Q→Qh滿足以下的正交性和近似性[18]:

(u-juu,vh)=0,?u∈X,?vh∈Dh,

(p-jpp,qh)=0,?p∈Q,?ph∈Dh,

‖u-juu‖0+h|u-juu|1≤

Chr+1‖u‖r+1,?u∈X∩Hr+1(Ω)，

‖p-jpp‖0+h|p-jpp|1≤

Chr+1‖p‖r+1,?p∈Q∩Hr+1(Ω)，

‖u-juu‖0,∞+h|u-juu|1,∞≤

Ch‖u‖1,∞,?u∈X∩W1,∞(Ω)

(4)

下面我們給出NS方程的非線性局部投影穩定的空間半離散格式.?t∈(0,T), 求(uh(t),ph(t))∈Xh×Qh, 滿足,?(vh,qh),

(?tuh,vh)+ν(?uh,?vh)+b(uh;uh,vh)-

(ph,?·vh)+Sconv(uh;uh,vh)=f,vh，

(qh,?·uh)+Spres(ph,qh)=0

(5)

其中

Sconv(uh;uh,vh)=

其中α1,M和α2,M分別為相應于對流項和壓力梯度項的局部投影穩定參數, 并且滿足以下假設.

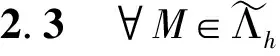
α1,M=α1hm1,α2,M=α2hm2，

其中m1,m2為穩定參數的階,其具體數值在后文的誤差分析中給出.

3 含穩定項的全離散格式

接下來我們對空間半離散格式(5)做時間上的有限差分.一般說來,時間差分上的全隱格式為無條件穩定,但每層時間上需解一個非線性方程組，全顯格式在計算模擬時具有優勢,但為了格式的穩定性需對時間步長Δt有諸多限制.一種通常的做法是線性項采用隱式格式,非線性項采用顯示格式. 下面我們給出(5)的不同時間差分格式.

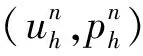
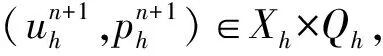
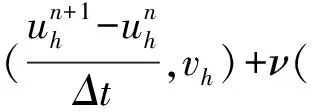
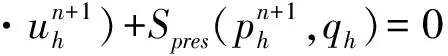
(6)

其中

注意到該格式中的非線性局部投影項實為線性型:

此時從程序實現時做數值積分的角度可知, 該項等價于以下兩種線性化對流項的局部投影：

(1) 高階term-by-term穩定項[11]

(2) SUPG-type的局部投影穩定項[16]

(κM((uM·?)uh),κM((uM·?)vh))M.

其中uM為流場速度u的局部投影平均

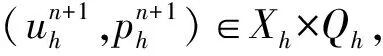
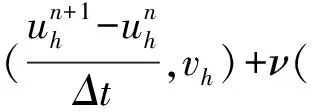
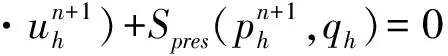
(7)

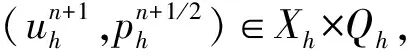
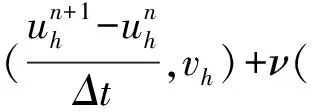
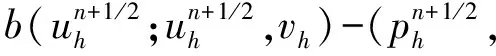
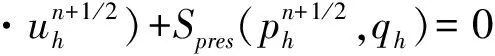
(8)

其中

下文我們將給出格式2的穩定性和收斂性分析.在前面的討論中我們知道,格式1中的非線性局部投影穩定項可等價于文獻[16]中提出的SUPG-type的穩定項和文獻[11]中的高階term-by-term穩定項.為簡潔起見,我們略去格式3中離散解的穩定性和收斂性分析.

4 穩定性與收斂性分析

本節我們給出全離散格式(7)的穩定性與收斂性分析.為此我們需要一些必要的假設和不等式, 并且為了記法的簡潔,我們定義

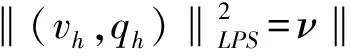
?(vh,qh)∈Xh×Qh.

在算子Π的定義中，曾假設Π具有局部穩定性及近似性[18]，即

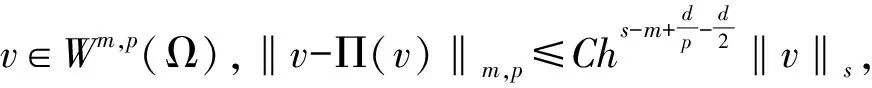
‖Π(v)‖0,M≤C‖v‖0,M.

注1有好幾類算子滿足上式給出的最優近似性和局部穩定性,如文獻[19]中的Scott-Zhang-like算子以及文獻[20]中的插值算子.

如文獻[12,21]中所述, 誤差分析要做到與1/ν一致的關鍵在于Bertoluzza所證明的離散commutator 性質, 即

引理4.2對于任意的u∈W1,∞(Ω),vh∈Vh，以下不等式成立:

‖(I-Π)(u·vh)‖0≤Ch‖u‖1,∞‖vh‖0.

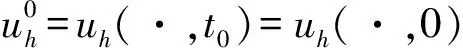
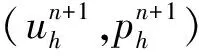
(9)

再次利用Cauchy-Schwarz不等式得

利用上兩式,再將(7)式乘上2Δt,并從0加到n得

對任意的1+Δt

利用

C0(N+1)≥Δt?

定理4.4(離散壓力的穩定性) 對任意的ph∈Qh, 存在一個與h,Δt和ν無關的正實數β, 使得

β‖ph‖0

(10)

證明 由連續inf-sup條件可知, 對任意ph∈Qh?Q, 存在v∈X使得

?·v=ph,|v|1≤C‖ph‖0.

由Green公式,(4)式中給出的算子ju的正交性和近似性以及Poincaré不等式可得

(?·(v-juv),ph)+(?·juv,ph)=

-(v-juv,κh?ph)+(?·juv,ph)≤

Ch|v|1·‖κh?ph‖0+(?·juv,ph).

又由ju:X→Xh有

定理得證.

定理4.5(離散速度的誤差估計) 令(u,p)∈X×Q為問題(1)的解.我們假設?tf∈L∞(L2)及(u,p)有額外的正則性,即(u,p)∈C0(Hs+1)×C0(Hs+1).又令存在常數C, 使得

‖?tu‖L∞(Hs+1)+‖?ttu‖L∞(L2)+

‖u‖L∞(W1,∞)≤C.

(11)

證明 記

E1+E2+E3+E4+E5+E6.

由Young不等式可得

由

Cauchy-Schwarz不等式, Young不等式及(4)式可得

關于對流項之差，我們將其分成如下形式：

E21+E22+E23+E24+E25,

這里我們利用了b(u;v,v)=0. 由Cauchy-Schwarz不等式,u的正則性,(4)式,逆不等式以及Young不等式有

類似地,有

及

對于第二項, 我們采用文獻[9]中的技巧,有

令

在方程式(2)中取時間t=tn+1后減去(7)式, 取測試函數為

(v,q)=(vh,qh)=

后有

對于上式(4)右端第一項, 我們有

將(4)式及逆不等式應用于上式第一項可得

對于最后一項, 我們再一次利用不等式

‖juun‖Wk,∞≤‖un‖Wk,∞,k=0,1

以及(4)式, 逆不等式和算子Π的穩定性,得

由逆不等式和(4)式,我們得到了最后一項的估計如下：

由引理4.2有

由以上估計, 我們有

對于第三項E3, 運用Cauchy-Schwarz不等式, Young不等式以及(4)式有

然后, 由分部積分, 算子ju的正交性, Cauchy-Schwarz不等式及Young不等式有

對于E5, 我們將其分成兩部分

由Young不等式可得

于是

C+ChM‖un+1‖1,M,∞+‖un+1‖1,M,∞.

對于剩下的部分, 由三角不等式及(4)式

從而由u∈L∞(W1,∞(Ω))可得

C(h2+1)h2s+m1‖u‖L∞(Hs+1).

于是

C(h2+1)h2s+m1‖u‖L∞(Hs+1).

類似可得

最后, 我們得到E6的估計

結合以上估計式,分別取m1,m2=0,2,再由逆不等式和范數‖·‖LPS的定義可得

在上式不等號左右同時乘上Δt,并且從0加到n,再由引理4.2可推出

最終, 由三角不等式和算子ju,jp的近似性, 定理得證.

定理4.6(離散壓力的誤差估計) 令速度誤差估計中的條件成立,且時間和空間的劃分具有相同的階, 即存在與h和Δt無關的常數C, 使得Δt≤Ch.于是我們可得如下的壓力誤差估計：

C(1+(1+ν2+Eu(1+h-d))/β2)Eu+

C/β2(1+h2+Eu)Su

(12)

其中我們令離散速度的穩定性和誤差估計的右端項分別為

和

(Δt)2.

證明 我們采用速度誤差方程中相同的誤差分解, 在(2)式中令時間t=tn+1后減去(7)式, 并令測試函數(v,q)=(vh,qh)=(vh,0)可得壓力的誤差方程

采用估計E1時的類似技巧和Poincaré不等式可得

不同于E2的估計, 這里我們采用文獻[9]中給出的方法來估計對流項之差

|T2|=|b(un+1;un+1,vh)-

對上式第二項,我們采用分部積分得

T21+T22.

由逆不等式知

于是

由Cauchy-Schwarz不等式,‖·‖LPS的定義和速度誤差估計的運用可以得到

至于T5,由離散速度的穩定性和離散Cauchy-Schwarz不等式可得

即

最后, 我們有

利用Δt≤Ch,結合以上的估計式可得

最終,由三角不等式,(4)式以及離散壓力的穩定性，定理得證.