圖形與幾何教學中培養學生推理能力的策略

黃輝煌

【摘要】在小學數學學習過程中，學生數學推理能力的培養非常重要.推理能力可以鍛煉學生的數學學習思維，開闊學生的數學視野.良好的數學推理能力也是解決數學問題的關鍵因素.筆者結合自己的一線教學實際情況，對小學生數學推理能力的培養提出了一些看法，希望能為廣大一線教師提供參考.

【關鍵詞】小學數學;推理能力;培養;策略

一、背景分析

落后理念和評價欠缺引發“短視”：日常教學中，很多教師還未真正理解現代教育理念，他們一直處于應試教育影響下，認為讓學生掌握知識即可，其他方面不納入考慮范圍.之所以會出現這種情況，主要是因為教師未能從正確的角度看待教學工作.有些教師的眼中通常只有數學教學內容，他們很少意識到數學思想的存在和學生基本能力的培養.除此之外，對學生進行評價也是教學工作的重要組成部分，然而即使處于新課改環境下，依然存在“評價”問題，即“雙基”，這是我國傳統評價方式，其所產生的影響至今還存在.評價導向在此方面也有著極大的影響，很多教師以此作為忽視培養學生數學能力、基本能力的借口，久而久之就形成了“短視”，這使學生在數學學習中的推理能力一直沒有得到有效提升.此外，新課程改革明確指出小學數學教學應達到“兩個權重”，即應該注重演繹推理和合理推理，不可再出現將教學重點集中在證實已經存在的結論上，而忽視探索過程的情況.然而，許多教師在實際教學中未能做到這一點.

二、小學生的數學推理能力培養策略

基于以往的教學經驗，筆者以圖形和幾何知識為例，建立了培養學生合理推理能力的相關策略框架，即階段差異化實施策略、類別針對性實施策略以及教學優化的實施策略.

（一）基于年段差異，實施漸進式、差別化的培養策略

新課標針對此方面曾做出說明，即數學教學中，推理占據著十分重要的地位，可以說是貫穿始終，然而推理能力并不是一朝一夕能夠獲得的，其需要較長時間的沉淀，以及教師的悉心指導.為了更好地實現這一目標，從小學階段開始，教師應將推理能力融入課堂教學中.值得注意的是，小學生的年齡差異較大，同樣的教學方式無法滿足所有階段的學生，因此差異化教學應根據學生的低、中、高三個階段的實際情況而定.

1.小學低段：引導學生感受推理過程

低段的學生以簡單推理為側重點，即“非黑即白”.以圖形與幾何為例，教師可以最簡單的方式開展教學，即為學生展示圖形，并讓學生自行分辨.此過程要兼具順序與條理，最重要的是，教師應使學生養成利用自己的語言將推理過程講出來的習慣.

[案例1]材料的個數

出示材料：●○●○○●○○○●（? ）●○○○○○，括號內應填（? ）球，要填（? ）個.

感受 1：顏色推理.讓學生用自己的語言描述，感受判斷依據.

感受 2：個數推理.根據規律判斷個數，感受判斷過程.

感受 3：適當抽象.教師引導學生用類似“1、1、1、2、1、3…”的方式逐漸感受“黑球永遠是一個，白球逐漸增加”的分配規律.

在較低階段，推理仍處于啟蒙階段.

2.小學中段：引導學生學習和體驗合理的推理方法

在小學低段學習的基礎上，此階段學生的學習能力有所提高.但是，教師要注意，在教學過程當中要循循善誘，循序漸進.

[案例2]具有相同周長的矩形的面積變化規律

出示材料：有一根40厘米細繩，將其圍成長方形，邊長是整厘米數，如何得到最大面積的長方形？

教師以“獨立思考—枚舉比較—猜想驗證—獲取方法—促進應用”的方式組織教學.

其優勢之一在于能夠讓學生將自己的學習成果得以具體應用，同時能夠以結果作為事實基礎，使后續學習事半功倍.

3.小學高段：指導學生使用“有問題”的推理來解決問題

在小學高段，教師要指導學生充分利用生活經驗、現有的數學知識和推理方法，獨立推理和解決問題.

[案例3]問題出發的合情推理

基本材料：自行車通過這座橋，車輪轉了幾周？

師：單憑問題，猜想已知條件是怎樣的.

生：橋長和車輪直徑可以是已知的.

師：解決這個問題，算式可能是什么？

生：可能是大橋長度 ÷ 車輪周長.

師：如果用 2000÷（3.14×0.6）解決這個問題，你有什么推測？

生：2000是橋的長度，0.6是車輪的直徑，整個算式是車輪轉的周數.

這個案例激發學生從問題進行反思.相較于教師常用的“例題講解—獲得方法—練習鞏固”這樣固定的“單行線教學方式”，本案例所實踐的“提出問題—合情推理—解決問題”這種反向結構可使共同的“前進教學，反復實踐”成為“雙向建構”.

（二）基于類別特點，實施針對性、相融合的應用策略

合理推理可分為兩類，一類是不完全歸納推理;另一類是類比推理.在教學中，教師既要考慮學生的特點，又要考慮教學內容的特點，同時不能忽視合理推理的特點.只有這樣，才能夠充分保證教學效率.

1.不完全歸納推理的應用策略——厚積薄發

所謂不完全歸納，其主要是以部分對象為目標，通過對其的推理來向全部對象過渡.這種方法的優勢在于學生通過自主思考獲取新知識，同時明白過程的重要性.但要注意以下兩點：

（1）學生養成在生活和學習中仔細觀察的習慣.

（2）學生應善于發現問題，積極探索，并與教師、同學交流.

[案例4]矩形區域計算方法（不完全歸納推理）

在方格中自由地涂出一個或幾個長方形，并記錄下來.

教師要求學生在方格上畫畫，并與學生分析長方形的構成，以便使學生更深入地了解長方形區域的計算公式.

2.類比推理的應用策略——瞻前顧后

類比推理是一種特殊的推理方法.當學生遇到新問題時，可以考慮相關的“前”知識.教學時要注意以下兩點：

（1）收集盡可能多的屬性，并積極探索兩個知識之間的共性.

（2）注意差異分析并獲得最全面的知識.

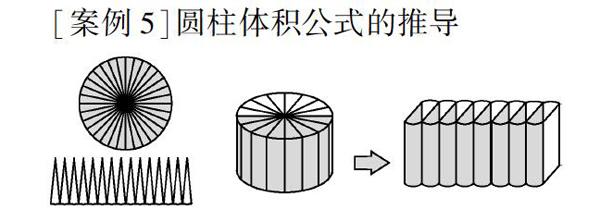
[案例5]圓柱體積公式的推導

學生在學習中要具備舉一反三的能力，在學習圓柱體積公式推導的過程中，除了鞏固平面圖形的面積推導以及學會立體圖形的面積推導外，其他相關問題也要有所思考.

（三）基于教學優化，實施有預設、重體驗的教學策略

教師在培養學生推理能力的過程中，采用適當的教學方法也是至關重要的.一般來說，教師在課堂教學中培養學生的推理能力應該由淺入深，慢慢推進.

1.基于課堂教學的整體優化，培養學生推理能力

[案例6]自編教材：局部關系推理整體關系

（1）初步感受

如下圖，正方形的邊長是8厘米，求圖中陰影部分的面積.

學生解答：a.8×2-3.14×42;b.8×2-22×4;c.8×2-3.14×12×16.觀察思考：不計算，對結果有什么猜想？

（2）同類再現

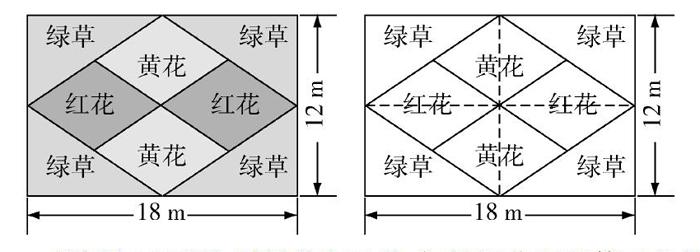
校園里有一塊長方形的地，學校想種上紅花、黃花和綠草.其中一種設計方案如下圖所示.你能分別算出紅花、黃花、綠草的種植面積嗎？

教師出示習題，引導學生反思：如果綠草面積等于花的總面積，這種設計方案是否可用？

2.基于課堂教學的局部優化，培養學生的推理能力

（1）仔細設計材料并創建推理平臺

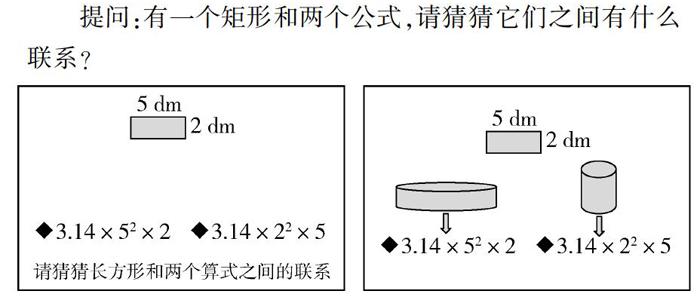
[案例7]推理圖形與算式之間的聯系

提問：有一個矩形和兩個公式，請猜猜它們之間有什么聯系？

教師故意預設“空白”，激勵學生根據現有信息進行推理，培養空間觀念，增強推理能力.

（2）引導觀察猜想，激發合情推理欲望

在“圖形與幾何”的教學中，教師要注重引導學生用數學的眼光觀察，看到表面背后的含義，并引導學生主動猜想，激發其進行合情推理的欲望.

三、結束語

推理能力是學生學習數學的重要組成部分.基于本研究成果和困惑，筆者將在“數與代數”等領域開展進一步研究，期待在培養小學生合情推理能力方面獲得更完整的認識和實踐策略.

【參考文獻】

[1]梁仁東.合情推理在小學數學四個領域中的應用[J].海峽科學，2013（7）：95-96.

[2]袁志祥.合情推理在小學數學中的運用[J].教育藝術，2013（5）：70.

[3]陳祥彬.在小學數學教學中培養學生的合情推理能力[J].小學數學教育，2012（11）：7-10.

[4]曹培英.小學數學合情推理的教學研究[J].小學數學教師，2015（Z1）：8-15.

[5]王曉利.小學生合情推理能力培養的策略研究：以五、六年級為例[D].南京：南京師范大學，2011.