基于神經網絡的航空發動機進口總壓畸變重構研究

(中國飛行試驗研究院，西安 710089)

1 引言

隨著航空技術的不斷發展，現代戰斗機的飛行速度和機動性不斷提高，航空發動機遭遇的進氣總壓畸變也更加嚴重[1-2]，傳統采用預留足夠穩定裕度的發動機穩定性設計方法所造成的發動機性能損失將變得不可接受。為解決發動機性能和穩定裕度的矛盾，畸變容限控制技術得到了發展和應用[3]。畸變容限控制技術將發動機進口畸變特征參數加入到發動機控制系統中，根據進氣畸變水平動態調節發動機的穩定工作裕度，在畸變小時減小穩定裕度以提高發動機性能，在畸變較大時擴大穩定裕度以確保發動機穩定工作[4]。NASA 在1983 年至1987年和1993年至1998年分別開展了HIDEC(高度集成度數字電子控制)項目[5-6]和HISTEC(高穩定性發動機控制)項目[7-8]，目的就是演示驗證發動機穩定性增強技術。

發動機畸變容限控制技術實現的一個重要基礎，是在飛行中實時估算發動機進口總壓畸變水平。在發動機穩定試驗和試飛中，通常采用在發動機進口安裝流場測量耙的直接測量方法獲取進口流場數據[9-11]。但由于飛行中機體振動、過載大，測量耙長期裝機使用一旦出現結構損壞將嚴重威脅飛機安全[12]，因此測量耙的流場測量方式并不適用于畸變容限控制技術。HIDEC項目基于飛行控制、大氣數據等預測攻角、側滑角的變化間接表征發動機進口流場畸變的變化[5-6]；HISTEC 項目則采用了基于有限測量的流場畸變估算方法，通過測量少量的內、外壁面動態靜壓解算發動機進口總壓畸變指數[7-8]。HISTEC 項目研究結果表明，基于壁面靜壓數據的總壓畸變重構方法較基于飛行參數的畸變預測方法準確性更高，且該方法僅與發動機進口流場分布有關，重構效果不受配裝發動機的影響，所建立的分析模型通用性較強。法國航空航天實驗室的Grenson等[13]基于S彎進氣道非定常數值仿真流場結果，分別采用神經網絡、線性隨機估計和二階隨機估計方法，驗證了基于壁面靜壓進行總壓畸變流場和畸變指數重構的可行性。國內學者在畸變預測方面也有所研究[14-15]，但鮮有涉及畸變容限控制的畸變實時解算方面的工作。本文以某型飛機進/發試飛數據為基礎，采用神經網絡方法開展發動機進口總壓流場和穩態周向畸變指數的重構研究，并對模型重構準確性和適用性進行分析，以期為國內航空發動機畸變容限控制技術的研發和應用提供參考。

2 建模數據樣本

進氣總壓畸變重構研究以某型飛機進氣道/發動機相容性試飛測量數據為基礎，包括發動機進口截面穩態壓力數據和關鍵飛行參數。試飛時進氣道流場測量采用6耙/30測點的方案，包括30路穩態總壓和6路壁面靜壓。發動機進口穩態壓力測點分布如圖1 所示，6 支測量耙等角度均布，耙上測點按照等環面原則分布(環面1～5 依次由內至外)；壁面靜壓測點與測量耙在同一截面等間隔分布。

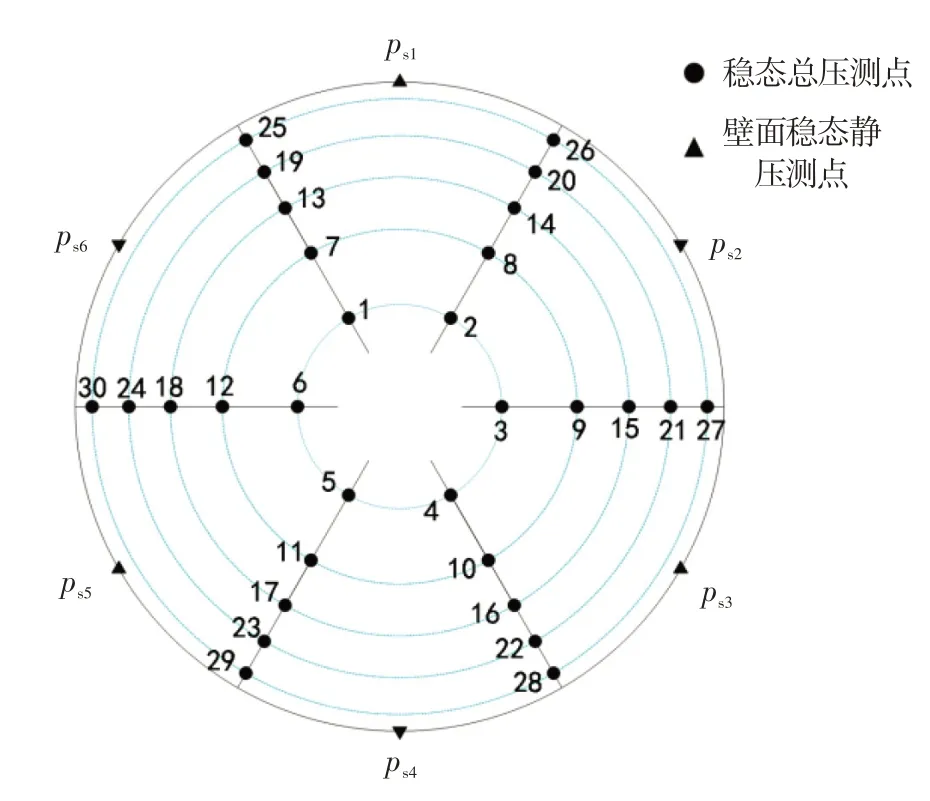
圖1 發動機進口面穩態壓力測點分布Fig.1 The steady pressure probes layout on the engine inlet face

試飛中穩態壓力和飛行參數采樣頻率為16 Hz，單架次記錄數據達到35 000至45 000行，為了在保留數據有效信息的同時降低數據規模和后續計算量，將試飛數據中相近的樣本剔除。考慮到本文研究主要以壁面靜壓作為畸變重構的輸入參數，故采用壁面靜壓作為篩選判斷條件。數據分析發現，穩態飛行過程壁面靜壓波動幅值不大于0.3 kPa，故將0.3 kPa作為數據篩選時的判定標準：若任意一個壁面靜壓測點在不同時刻記錄的數據之差絕對值大于0.3 kPa，則判定這兩個樣本為不同樣本，均存儲到篩選樣本集中；反之，則認為是相同樣本，僅存儲最先遇到的樣本。采用該方法對所有架次試飛數據進行篩選，總數據樣本減少到了13 880 行，有效降低了樣本規模。

3 畸變重構的神經網絡方法

發動機進口流場畸變重構研究采用BP 神經網絡方法，并利用型號試飛數據對神經網絡模型進行訓練，建立基于壁面靜壓或組合數據的發動機進口總壓畸變重構模型。神經網絡模型分別以30 個穩態總壓測點數據和穩態周向畸變指數[1]為重構目標，采用不同的輸入參數組合，建立了三種BP 神經網絡模型，具體見表1。由于實際試飛測量中未測量發動機進口中心點的總壓，為了分析中心點總壓對畸變重構結果的影響，采用最內環6 個測點的總壓平均值等效作為發動機進口中心點總壓(以下簡稱中心點總壓)。基于三種神經網絡模型結構，分別建立總壓流場分布重構神經網絡模型和畸變指數重構神經網絡模型。所有神經網絡模型均采用3層神經網絡結構，2 層隱含層神經元數均為30。神經網絡訓練時將13 880 組樣本按比例隨機分為三個樣本集：70%的樣本作為訓練樣本集，參與神經網絡訓練；15%的樣本作為驗證樣本集，用于在訓練過程中檢查模型的泛化能力和判斷是否出現過擬合；另外15%的樣本作為最終的測試樣本集，用于神經網絡最終的泛化能力測試。后文中均是在測試樣本集上對各神經網絡模型進行對比。

表1 神經網絡模型輸入輸出參數Table 1 The neural networks input and output parameters

4 神經網絡模型重構結果分析

4.1 總壓流場重構分析

圖2給出了三種神經網絡模型對各自測試樣本集30 個總壓測點數據的重構誤差概率分布。可以看出，神經網絡模型重構的總壓測點誤差呈正態分布，三種模型的重構誤差在±正態分布范圍內的分布概率分別是97.80%、99.47%和99.67%，模型2 和模型3 較模型1 具有更優重構精度。圖3 為測試樣本集上三種神經網絡模型對30 個測點總壓數據重構的均方誤差(MSE)。圖中，ave為30個測點總壓數據重構均方誤差的平均值，測點編號參見圖1。可以看出，模型1除測點5外各測點重構的均方誤差都小于0.9 kPa，平均值小于0.8 kPa；模型2和模型3各測點重構的均方誤差均小于0.6 kPa，平均值小于0.5 kPa。在模型1輸入參數基礎上，模型2增加了中心點總壓，使得模型對總壓測點的重構準確性較模型1大幅提高；模型3輸入參數繼續加入攻角、側滑角后，各測點總壓重構均方誤差進一步降低。

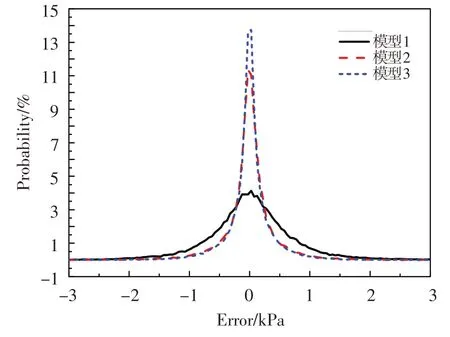
圖2 神經網絡模型總壓重構誤差概率分布Fig.2 The probability distribution of total pressure reconstruction error of the neural networks

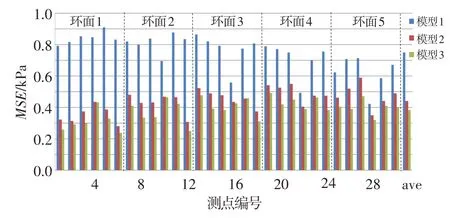
圖3 神經網絡30個總壓測點重構的均方誤差Fig.3 The mean square error of 30 reconstructed total pressure probes data of the neural networks

圖4給出了三種模型所對應的測量耙各個測量環面(見圖1)總壓測點重構結果的均方誤差平均值。與發動機5環面/30測點的總壓空間分布相比，建模所采用的6路壁面靜壓均位于發動機進口外壁面，僅為周向的一維分布。對于模型1，環面均方誤差由外(環面1)至內(環面5)逐漸增大，最外側環面與壁面靜壓測點距離最近、相關性最強，重構準確性也最高；壁面靜壓對發動機進口中心區域流場的表征能力不足。模型2和模型3引入中心點總壓后，不僅使得整個測量截面測點的重構均方誤差大幅降低，而且還使得各個環面重構均方誤差的差異減小。模型2和模型3環面重構均方誤差平均值自內環向外環先增大后減小，最大出現在4環面，為中心點總壓和外壁面靜壓綜合影響的結果，仍符合環面總壓重構準確性隨著距離中心點或外壁面的距離的增加而降低。因此，內、外徑兩個維度的壓力數據對于實現畸變流場分布的高精度重構必不可少。

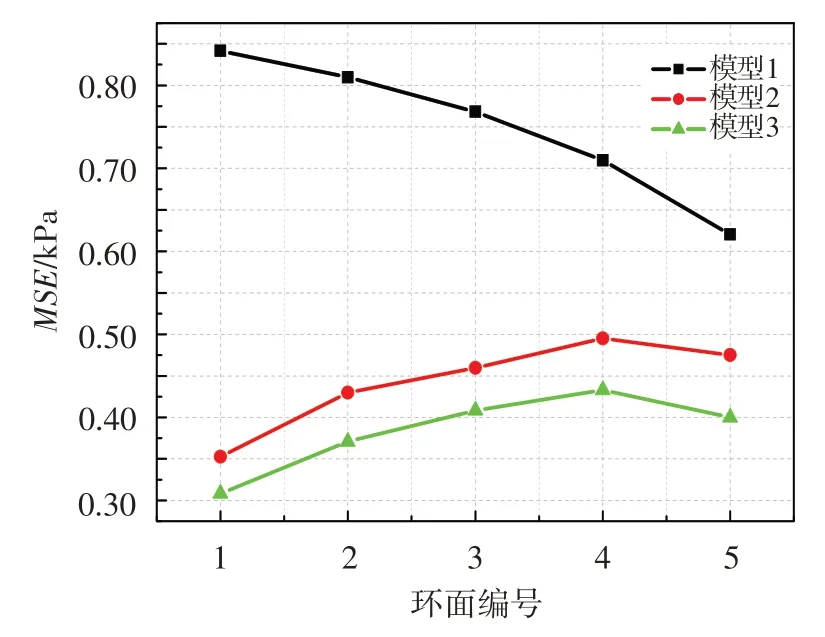
圖4 測量耙各個環面總壓重構的均方誤差平均值Fig.4 The average mean square error of reconstructed total pressure of every ring on the rake

圖5、圖6分別給出了相同發動機工況下飛機平飛和攻角、側滑角組合飛行狀態，三種神經網絡模型對發動機進口30 個測點總壓數據重構結果的均方誤差平均值和飛行參數的時間歷程。可見，對于平飛狀態，三種模型的均方誤差平均值都較小，模型2和模型3 的重構準確性相當。對于攻角、側滑角組合飛行狀態，當出現較大的負側滑角時，模型1和模型2 的總壓數據重構均方誤差平均值明顯增大，而模型3 的重構均方誤差平均值較小且基本維持穩定。模型1和模型2的重構結果對攻角的變化不敏感，當側滑角較小時，攻角達到11.0°，其重構結果與模型3 的相當；但模型1 和模型2 對側滑角較敏感，當側滑角超過-7.5°時，其重構結果較模型3 的均方誤差平均值快速增大。

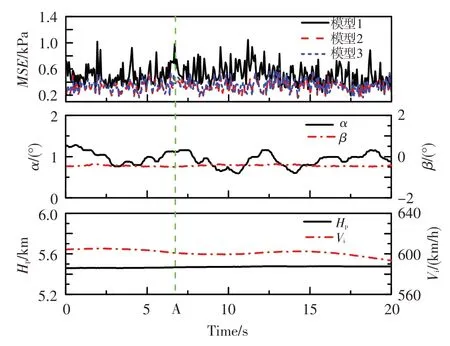
圖5 飛機平飛狀態神經網絡模型的重構結果Fig.5 The reconstruction results of the neural networks in the level flight

圖7、圖8分別為圖5中A時刻和圖6中B時刻，根據原始測量數據和三種模型重構數據繪制的發動機進口總壓流場分布云圖。對于平飛狀態，三種模型都可獲得較為準確的流場分布，但模型1 重構結果的高壓區壓力相對偏低。對于攻角、側滑角組合飛行狀態，模型1和模型2的重構結果相似，低壓區范圍和形狀都較原始圖譜有較大差別，特別是未能重構出中心區域的低壓區；而模型3重構結果的高、低壓區范圍和形狀都與原始圖譜吻合良好。綜上，對于具有較大攻角和側滑角的飛行狀態，將攻角和側滑角加入模型輸入參數，可顯著改善發動機進口流場畸變重構的準確性。

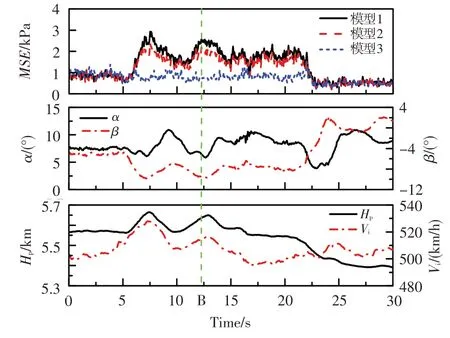
圖6 攻角、側滑角組合飛行狀態神經網絡模型的重構結果Fig.6 The reconstruction results of the neural networks in the maneuvering flight

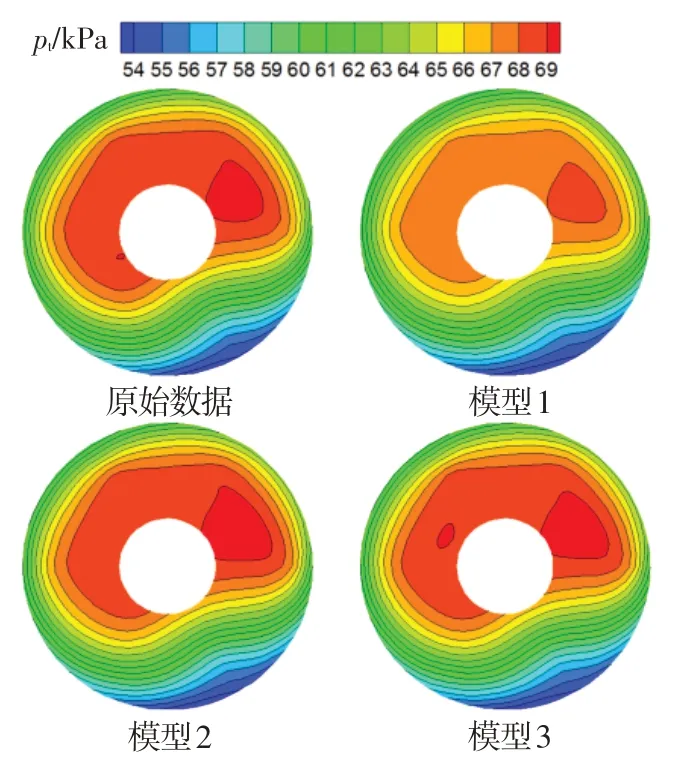
圖7 平飛過程發動機進口流場重構結果云圖Fig.7 The reconstructed engine inlet flow field in the level flight

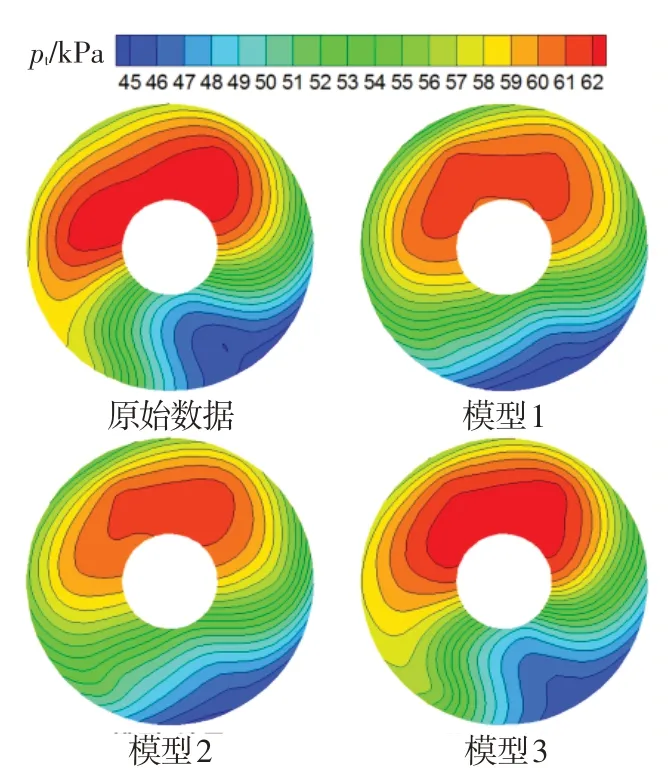
圖8 攻角、側滑角組合飛行過程發動機進口流場重構結果云圖Fig.8 The reconstructed engine inlet flow field in the maneuvering flight

4.2 穩態周向畸變指數分析

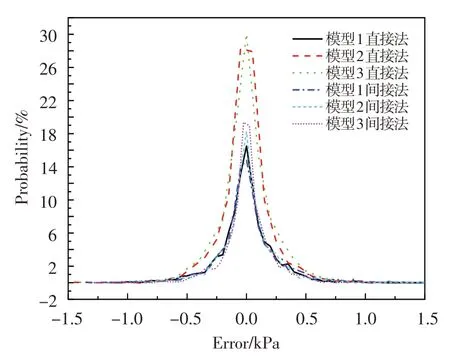
圖9 直接法和間接法各模型穩態畸變指數重構結果誤差概率分布Fig.9 The distortion index reconstructing error probability distribution of the indirect and direct methods

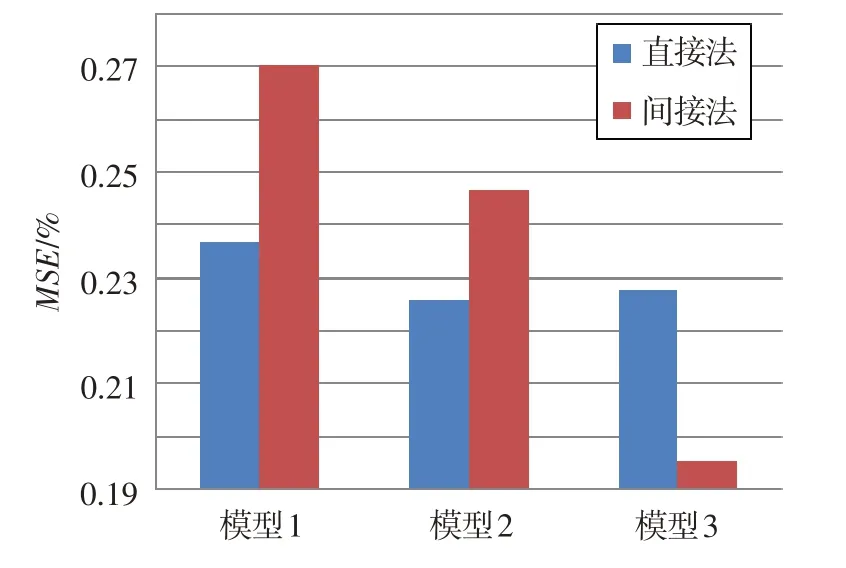
圖10 直接法和間接法穩態畸變指數重構均方誤差對比Fig.10 The distortion index reconstructing mean square error comparison of the indirect and direct methods

5 神經網絡重構模型適用性分析

為分析訓練獲得的總壓畸變重構神經網絡模型的適用性，采用另一型飛機的進氣道測量數據驗證三種神經網絡模型的總壓流場分布和畸變指數重構效果。該型飛機與建模數據來源飛機具有相同的進氣道結構和布局，但配裝發動機不同；進氣道流場測量采用了與圖1相同的測點布置方案，總、靜壓測點相對位置也與建模數據來源飛機的相同。

5.1 總壓分布重構模型適用性分析

圖11為該試驗機在11 km高度飛行過程中三種神經網絡模型對發動機進口總壓分布重構結果的對比，該飛行過程包括平飛、大攻角飛行和側滑飛行，具有一定的代表性。圖中，MSEav為同一時刻30 個測點總壓數據重構均方誤差的平均值，N1為發動機低壓轉子轉速。可以看出，模型1 的重構均方誤差較大且對發動機轉速較敏感，當N1大于90%時MSEav達到10 kPa左右；模型3的總壓數據重構結果最佳，30個測點的平均均方誤差在2 kPa以內，但較圖5和圖6結果偏大。圖12為對應圖11中C時刻模型3重構的總壓分布與原始數據總壓分布的對比。C時刻飛機具有-8°的側滑角，進氣畸變較大。模型3很好地重構出了低壓區位置，但低壓區范圍較原始圖譜偏大。由此可得出，模型3 在總壓流場分布重構方面對于具有相同進氣道結構的飛機有一定的適用性，但與建模飛機發動機進口流場重構結果相比重構準確性偏差。

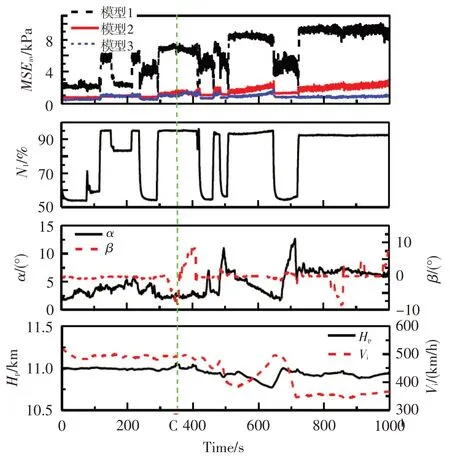
圖11 三種模型總壓流場重構結果對比Fig.11 The comparison of 3 neural networks in total pressure reconstructing results

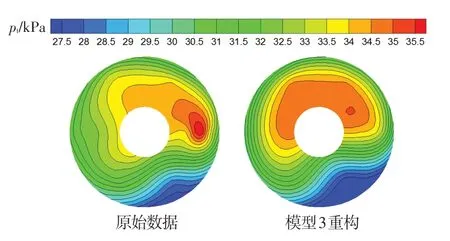
圖12 模型3重構圖譜與原始數據圖譜對比Fig.12 The comparison of the model 3 reconstructed pattern and original pattern

5.2 穩態畸變指數重構模型適用性分析

基于與圖11相同的飛行過程數據，對三種神經網絡模型采用直接法和間接法進行重構的適用性進行分析。重構均方誤差變化如圖13 所示，圖中MSE1、MSE2、MSE3分別對應模型1、模型2 和模型3的重構均方誤差。可以看出，三種模型中模型3的重構結果最好，但均方誤差較大(最大達到4%左右)，與圖9中建模飛機的測試樣本集畸變指數重構結果相比誤差較大。對于模型3，采用間接法的重構準確度略優于直接法。綜上，對于重構，三種神經網絡模型的直接法和間接法對于與建模飛機具有相同進氣道結構的飛機的適用性不佳。

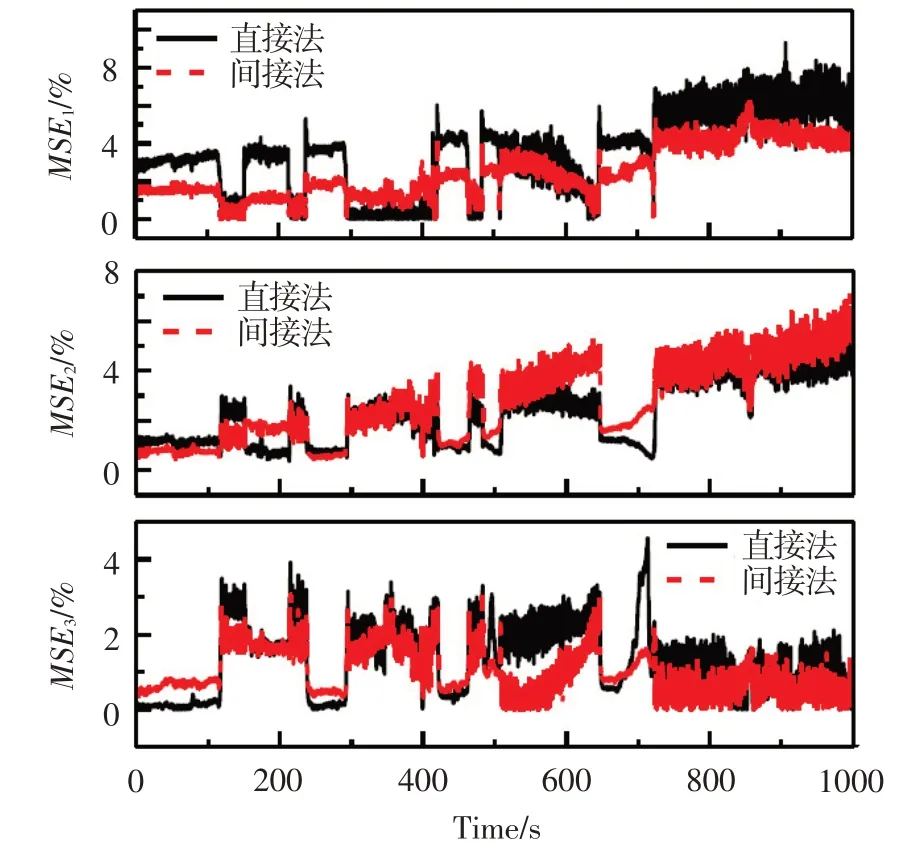
圖13 三種神經網絡模型穩態周向畸變指數重構結果對比Fig.13 The comparison of distortion index reconstructed results of three neural networks

6 結論

以某型飛機發動機進口流場壓力測量數據和飛行數據為基礎，基于神經網絡方法，開展了采用壁面靜壓、中心點總壓、攻角、側滑角參數重構發動機進口總壓畸變的研究，主要結論如下：

(1)采用神經網絡方法，基于壁面靜壓、中心點總壓以及攻角、側滑角，可以較為準確地重構發動機進口流場總壓分布和穩態周向畸變指數；

(2)單純以外壁面靜壓作為輸入的神經網絡模型對于發動機進口內環面的重構效果不佳，輸入參數加入中心點總壓后可大幅提高各個環面的總壓重構準確性，而進一步引入攻角、側滑角參數后可以改善神經網絡模型對于大攻角、側滑角飛行狀態的總壓流場和穩態周向畸變指數的重構準確性；

(3)以壁面靜壓、中心總壓和攻角、側滑角為輸入參數的神經網絡模型進行穩態周向畸變指數重構時，采用先重構流場總壓分布再計算穩態周向畸變指數的間接法可以獲得較好的重構準確性；

(4)對于具有相同進氣道結構和布局的另一型飛機，以壁面靜壓、中心點總壓及攻角、側滑角為輸入參數的神經網絡模型對于流場分布具有一定的適用性，重構流場可反映原始流場的主要特征，但對穩態周向畸變指數重構的適用性較差，重構偏差較大。