變截面功能梯度Timoshenko 梁的自由振動(dòng)分析

杜運(yùn)興，程鵬，周芬

（湖南大學(xué) 土木工程學(xué)院，湖南 長(zhǎng)沙 410082）

隨著科學(xué)技術(shù)的發(fā)展，各種高性能材料相繼出現(xiàn)，比如功能梯度材料（FGM），F(xiàn)GM 是一種微觀上不均勻的空間復(fù)合材料，通常由兩種或多種不同的材料組成.FGM 因性能優(yōu)異而廣泛應(yīng)用于土木、機(jī)械和航空航天等領(lǐng)域.一些學(xué)者對(duì)FGM[1]或FGM 結(jié)構(gòu)[2]進(jìn)行了研究.而FGM 梁通常作為單獨(dú)的結(jié)構(gòu)或者作為FGM 結(jié)構(gòu)的構(gòu)件應(yīng)用于工程中，對(duì)于一些受到動(dòng)荷載作用的FGM 梁，求解其固有振動(dòng)特性從而避免共振具有重要意義.目前，對(duì)于軸力作用下的變截面FGM 梁的自由振動(dòng)問(wèn)題的研究仍不完善，需深入研究.

對(duì)于材料性質(zhì)沿梁高分布的FGM 梁的自振問(wèn)題已有大量研究.基于Euler-Bernoulli 梁理論，Yang等[3]分析了帶有裂縫的FGM 梁的自由振動(dòng)和穩(wěn)定問(wèn)題.等[4]分析了FGM 梁在集中移動(dòng)簡(jiǎn)諧荷載作用下的自由和受迫振動(dòng).最近Lee 等[5]提出了一種精確傳遞矩陣法來(lái)分析FGM 梁的自由振動(dòng)特性.盡管基于Euler-Bernoulli 梁理論計(jì)算較為簡(jiǎn)單，但是在長(zhǎng)細(xì)比較小時(shí)結(jié)果誤差較大.龔云[6]分別基于Euler-Bernoulli 梁理論與Timoshenko 梁理論分析了FGM 梁自由振動(dòng)和彎曲問(wèn)題，結(jié)果表明長(zhǎng)細(xì)比對(duì)固有頻率影響顯著.基于一階剪切變形理論，Lee 等[7]研究了材料沿截面高度分布的FGM 梁的軸向-彎曲耦合振動(dòng).他還分析了FGM 梁法向應(yīng)變能和剪切應(yīng)變能固有頻率貢獻(xiàn)率的影響.該方法能準(zhǔn)確地評(píng)估剪切變形的影響，蒲育等[8]也提出一種改進(jìn)型廣義微分求積法來(lái)求解FGM 梁的自由振動(dòng)問(wèn)題.也有一些學(xué)者基于高階梁理論分析該問(wèn)題，比如，Pradhan 等[9]研究了不同邊界條件下FGM 梁的自由振動(dòng)問(wèn)題.基于不同的剪切變形梁理論以及經(jīng)典梁理論進(jìn)行了分析.[10]使用不同高階梁理論對(duì)FGM 梁的基頻進(jìn)行分析，結(jié)果表明使用各種高階梁理論所得結(jié)果差異很小.Karamanli[11]基于三階剪切變形理論研究了在多種邊界條件下，雙向FGM 梁的自由振動(dòng)特性.

上述研究的材料性質(zhì)沿厚度方向變化的FGM梁均是等截面梁.對(duì)于變截面梁的研究較少.Maganti等[12]分析了FGM 旋轉(zhuǎn)楔形梁的彎曲振動(dòng)，但并未考慮剪切變形的影響.Li 等[13]研究了變厚度FGM 梁在流體中的自由振動(dòng).

對(duì)于某些材料性質(zhì)沿厚度方向變化的FGM 梁，其物理中面可能與幾何中面不重合.一些學(xué)者[14-16]的研究表明，如果選擇合適的參考面即物理中面，就可以消除板振動(dòng)方程中的拉伸-彎曲耦合，這可以大大減小計(jì)算量.基于物理中面的概念，賈金政等[17]分析了FGM 梁的彎曲和過(guò)屈曲問(wèn)題，Larbi 等[18]基于高階梁理論分析了等截面FGM 梁的靜力和自由振動(dòng)問(wèn)題.但對(duì)于軸向力作用下的變截面FGM 梁的自由振動(dòng)問(wèn)題，還缺乏研究.因此本文基于物理中面的概念，對(duì)于變截面FGM 梁自由振動(dòng)問(wèn)題進(jìn)行研究.

在文獻(xiàn)[9-10]中，基于高階剪切變形梁理論所得的結(jié)果與基于一階剪切變形梁理論所得結(jié)果差異不大，因此，本文擬基于Timoshenko 梁理論對(duì)該問(wèn)題進(jìn)行研究，并考慮軸向力的作用.由于變截面FGM 梁的自由振動(dòng)方程為變系數(shù)微分方程組，無(wú)法用常規(guī)方法求解，故本文使用一種冪級(jí)數(shù)法對(duì)該變系數(shù)微分方程組進(jìn)行求解.通過(guò)本文方法容易求得變截面FGM 梁的固有頻率、振型以及臨界荷載，可為變截面FGM 梁的設(shè)計(jì)與應(yīng)用提供理論支持.

1 理論分析

一個(gè)變截面FGM 梁如圖1 所示，梁截面為矩形.梁的上表面材料為純陶瓷，下表面為純金屬.材料性質(zhì)P（z）包括密度ρ（z）、泊松比ν（z）、彈性模量E（z）的分布規(guī)律見(jiàn)式（1）.

式中：Pt、Pb分別表示梁頂面和梁底面的材料性質(zhì)；k是梯度指數(shù)，且k≥0.剪切模量G（z）和彈性模量的關(guān)系為：

根據(jù)式（1）和式（2），梁頂面剪切模量Gt=，梁底面剪切模量.

圖1 FGM 梁模型及參數(shù)Fig.1 Model and parameters of FGM beam

根據(jù)文獻(xiàn)[15]給出的物理中面的概念，可以給出梁物理中面的位置，即：

對(duì)于各向同性均質(zhì)梁，e0=0.

基于Timoshenko 梁理論，梁的位移函數(shù)可表述為如下形式：

式中：θ 為梁截面轉(zhuǎn)角；u 和w 分別是梁物理中面沿x 軸和z 軸方向的位移分量.

假設(shè)σzz=0，基于小變形的假設(shè)，根據(jù)位移函數(shù)可以得到相應(yīng)的應(yīng)變：

于是，梁的應(yīng)變能（U）和動(dòng)能（K）表示為：

式中：κ 為剪切形狀系數(shù).且

基于上述物理中面概念可知I2=0，但J2不一定等于0，若J2≠0，則會(huì)引起彎曲-軸向耦合振動(dòng).

假定梁的兩端邊界受到3 個(gè)作用力（如圖2 所示），分別是軸力N（x，t）、剪力Q（x，t）和彎矩M（x，t），因此外力做功（W）可以表述為：

使用哈密頓原理求解梁的振動(dòng)微分方程以及相應(yīng)的邊界內(nèi)力與位移之間的微分關(guān)系：

將式（6）（7）（9）代入式（10）中可得梁的振動(dòng)微分方程：

圖2 梁的邊界力Fig.2 Boundary forces of a beam

以及相應(yīng)的邊界內(nèi)力與位移之間的微分關(guān)系：

使用分離變量法，方程的通解具有如下形式：

式中：ω 是梁振動(dòng)的固有圓頻率；i 是虛數(shù)單位.將式（13）代入式（11）（12）中，無(wú)量綱化可得：

式（14）（15）中無(wú)量綱參數(shù)及變量見(jiàn)式（16）.

式（14）表示的微分方程的系數(shù)隨著X 的變化而變化.采用冪級(jí)數(shù)法求解該微分方程，其精確解表示成冪級(jí)數(shù)形式如下：

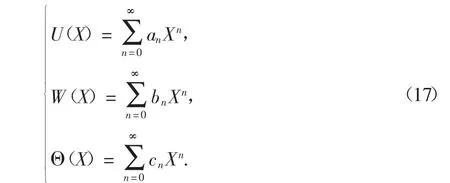
I1（X），I3（X），A1（X），T（X），J1（X），J2（X），J3（X）表示成多項(xiàng)式形式如下：

本文研究的變截面梁高度h（x）和寬度b（x）沿x軸方向變化，可以表示為：

式中：αh、αb為截面變化系數(shù)，在本文中，取αh=αb=α，當(dāng)α=0 時(shí)，梁為等截面梁.b0、h0分別為梁左端的截面寬度和高度.因此N1=2、N3=4、N4=2、N5=3、N6=4、N7=2，di、fi、gi、hi、ki根據(jù)式（8）（16）（19）確定.本文所研究軸力為常軸力，因此N8=0，t0=1.

將式（17）（18）代入式（14）中可得冪級(jí)數(shù)解的系數(shù)ai+2、bi+2和ci+2的遞推關(guān)系：

對(duì)于式（20），n≥0，其中，ai=0、bi=0 以及ci=0，當(dāng)i ＜0 時(shí).顯然，上述遞推關(guān)系需滿足d0、s2l0+τt0、f0不等于0.

利用上述遞推公式，式（14）的通解用矩陣可以表示為：

式中：Ui、Wi、Θi（i=1，2，3，4，5，6）均是式（14）的基本解.a0、a1、b0、b1、c0、c1為常數(shù)，它們可以通過(guò)邊界條件確定.

對(duì)于整個(gè)梁，其最左端（X=0）和最右端（X=L）的無(wú)量綱軸向位移、橫向位移、轉(zhuǎn)角、軸向力、剪力、彎矩可以由式（15）和（21）求出，因此，梁兩端的狀態(tài)向量可以表示為：

于是，根據(jù)式（23）和式（24）得：

其中，F(xiàn) 為六階方陣，通過(guò)它建立梁兩端狀態(tài)向量之間的關(guān)系，再結(jié)合具體邊界條件討論如下.

如圖1 所示，梁的邊界約束條件為非經(jīng)典邊界條件時(shí)，存在下列關(guān)系

寫(xiě)成矩陣形式，有：

結(jié)合式（28）和式（25）可得：

式中：δ1、δ2為系數(shù)向量，G 為六階方陣.于是可得：

對(duì)于上述方程，若有非零解，則其系數(shù)矩陣行列式必須等于零，即：

式（33）即為頻率方程，通過(guò)求解式（33）可得梁的第i 階無(wú)量綱固有頻率βi，根據(jù)無(wú)量綱固有頻率與固有頻率之間的關(guān)系即可得固有頻率.值得一提的是，通過(guò)調(diào)整邊界約束彈簧的剛度也可以求解經(jīng)典邊界條件下FGM 梁的固有頻率，在本文中，以簡(jiǎn)支FGM 梁為例，即取，然后可以根據(jù)式（33）求解相應(yīng)的無(wú)量綱固有頻率.

在得到無(wú)量綱固有頻率后，將它代入式（32），于是系數(shù)矩陣各個(gè)元素均為常數(shù).取U（0）=1，可以得到相應(yīng)的W（0）和Θ（0），進(jìn)而可求得狀態(tài)向量S1，再聯(lián)合式（23）可得積分常數(shù)向量d.于是可以得到梁的第i 階振型函數(shù)U（X）、W（X）和Θ（X）.

2 結(jié)果與討論

本文研究的FGM 梁的上表面的材料為純陶瓷（彈性模量為Et=380 GPa，密度為ρt=3 960 kg/m3，泊松比為0.3）；梁的下表面的材料為純鋁（彈性模量為Eb=70 GPa，密度為ρb=2 702 kg/m3，泊松比為0.3）.

2.1 結(jié)果驗(yàn)證與分析

由于本文振動(dòng)微分方程的解為冪級(jí)數(shù)解，實(shí)際計(jì)算中經(jīng)常采用近似解代替級(jí)數(shù)解，近似解選取級(jí)數(shù)解前N 項(xiàng)計(jì)算.理論上，N 越大，無(wú)量綱固有頻率近似解的精確度越高.為了探討近似解所取項(xiàng)數(shù)N對(duì)無(wú)量綱固有頻率精度的影響，以文獻(xiàn)[10]中的一個(gè)等截面簡(jiǎn)支FGM 梁（取α=0 來(lái)分析等截面梁）為例，梁長(zhǎng)與梁高之比1/μ 取5 和20，梯度指數(shù)k 取0、1、2，無(wú)量綱軸力τ 取0.由表1 中的數(shù)據(jù)可以發(fā)現(xiàn)本方法所得的頻率方程式（33）的解是收斂的，且近似級(jí)數(shù)解并不需要取太多項(xiàng).

表1 簡(jiǎn)支FGM 梁無(wú)量綱固有頻率計(jì)算值對(duì)比Tab.1 Comparison of dimensionless natural frequencies of simply supported FGM beam

計(jì)算所得結(jié)果與文獻(xiàn)[10]中經(jīng)典邊界條件下FGM 梁的無(wú)量綱基頻進(jìn)行比較，驗(yàn)證了所提出方法的有效性.且無(wú)量綱固有頻率隨梯度指數(shù)k 增大而減小.當(dāng)長(zhǎng)高比較大時(shí)所得的無(wú)量綱固有頻率大于相應(yīng)的長(zhǎng)高比較小時(shí)所得的數(shù)據(jù)，這反映了，長(zhǎng)高比較小時(shí)，剪切變形對(duì)無(wú)量綱固有頻率的影響較大，不可忽略.此外，結(jié)果還表明：通過(guò)調(diào)整邊界約束彈簧的剛度來(lái)求解經(jīng)典邊界條件下FGM 梁的固有頻率是可行的.

當(dāng)1/μ 取5 和10，梯度指數(shù)k 取1 時(shí)，簡(jiǎn)支FGM 梁的前四階振型函數(shù)U（X）和W（X）對(duì)比如圖3 所示.由圖可知，梁長(zhǎng)與梁高之比對(duì)梁的自振特性有顯著影響，當(dāng)1/μ 取5 時(shí)，第三階模態(tài)由軸向振動(dòng)主導(dǎo)，而當(dāng)1/μ 取10 時(shí)，第四階模態(tài)由軸向振動(dòng)主導(dǎo)，其他階模態(tài)均由彎曲振動(dòng)主導(dǎo).由于1/μ 值的大小反映了剪切變形的影響程度，1/μ 值越小，剪切變形影響越大，因此，剪切變形不僅會(huì)影響彎曲振動(dòng)，對(duì)軸向振動(dòng)也有影響.

圖3 簡(jiǎn)支FGM 梁的前四階振型函數(shù)U（X）和W（X）（從左到右分別為第一到第四階模態(tài)）Fig.3 The first four mode functions U（X）and W（X）of simply supported FGM beam（from left to right，the first to the fourth modes respectively）

2.2 截面變化系數(shù)對(duì)變截面FGM 梁自振特性的影響

使用本文方法計(jì)算簡(jiǎn)支FGM 梁無(wú)量綱固有頻率，取梯度指數(shù)k=1，梁長(zhǎng)與梁高之比1/μ 取100，截面變化系數(shù)α 取不同的值時(shí)，梁前五階無(wú)量綱固有頻率計(jì)算值見(jiàn)表2.由表2 中的計(jì)算結(jié)果可知，隨著截面變化系數(shù)α 增大，梁的無(wú)量綱固有頻率逐漸減小.另外，還討論了截面變化系數(shù)α 對(duì)簡(jiǎn)支梁前四階振型函數(shù)W（X）的影響，如圖4 所示，可以看出：隨著截面變化系數(shù)α 的增大，振型函數(shù)W（X）之間的差異逐漸增大.此外，右端差異較大，這是因?yàn)榱航孛鎻淖蟮接叶酥饾u變小從而使得剛度變小，于是變形就更大，但其形狀基本相同.

表2 截面變化系數(shù)不同時(shí)簡(jiǎn)支FGM 梁前五階無(wú)量綱固有頻率Tab.2 The first five dimensionless natural frequencies of the simply supported FGM beam with different section variation coefficients

圖4 截面變化系數(shù)α 對(duì)FGM 簡(jiǎn)支梁前四階振型函數(shù)W（X）的影響Fig.4 Influence of section variation coefficient α on the first four mode functions W（X）of the FGM simply supported beam

2.3 軸向荷載對(duì)FGM 梁自振特性的影響

當(dāng)軸向荷載作用于簡(jiǎn)支FGM 梁時(shí)，其固有振動(dòng)特性會(huì)隨軸向荷載的改變而改變，因此，對(duì)于軸向荷載作用下的FGM 梁需進(jìn)行進(jìn)一步研究.梯度指數(shù)k取1，截面變化系數(shù)α 取0，梁長(zhǎng)與梁高之比1/μ 取100.不同軸向荷載作用下FGM 梁的前五階無(wú)量綱固有頻率見(jiàn)表3.由表中數(shù)據(jù)可以看出：軸向荷載對(duì)基頻影響較大而對(duì)高階頻率影響較小，這是因?yàn)楫?dāng)軸向壓力快達(dá)到臨界荷載時(shí)，無(wú)量綱固有頻率才會(huì)大幅減小，而軸向壓力達(dá)到一階臨界荷載時(shí)，還遠(yuǎn)不到二階臨界荷載，因此對(duì)高階頻率影響較小.軸向壓力接近一階臨界荷載時(shí)，基頻會(huì)逐漸接近于0.

表3 不同軸向荷載作用下梁的前五階無(wú)量綱固有頻率Tab.3 The first five dimensionless natural frequencies of the beam under different axial loads

基于上述結(jié)論，在本節(jié)進(jìn)一步分析了對(duì)于不同截面變化系數(shù)α 和梯度指數(shù)k，基頻和軸向壓力之間的關(guān)系，同時(shí)分析k 和α 對(duì)FGM 梁的臨界荷載的影響.對(duì)于簡(jiǎn)支梁，選擇不同的k 和α 值，梁的基頻與軸向載荷之間的關(guān)系如圖5 所示.從圖中可以看出，隨著k 值的增大，F(xiàn)GM 梁的無(wú)量綱固有頻率都有所減小.此外，隨著k 值的增大，臨界荷載也大幅減小，這是因?yàn)椋S著k 值的增大，梁中鋁的含量增加從而使得梁的彈性模量和密度都減小，而密度的減小對(duì)臨界荷載沒(méi)有影響，因此k 值的增大會(huì)導(dǎo)致一階臨界荷載的減小.另外截面變化系數(shù)α 也會(huì)導(dǎo)致一階臨界荷載的減小.

圖5 梯度指數(shù)取不同值時(shí)懸臂FGM 梁的無(wú)量綱基頻與軸向力的關(guān)系Fig.5 Relation between dimensionless fundamental frequency and axial load of cantilever FGM beam with different values of graded index

3 結(jié)論

本文基于Timoshenko 梁理論，建立了變截面FGM 梁的自由振動(dòng)方程，采用冪級(jí)數(shù)法求解變截面梁振動(dòng)微分方程組.隨后以上表面為陶瓷、下表面為鋁的FGM 梁為例，研究了該方法的收斂性，并分析了長(zhǎng)高比、梯度指數(shù)、截面變化系數(shù)以及軸向力對(duì)固有振動(dòng)特性的影響，主要結(jié)論如下：

1）本文提出的方法收斂性良好，且具有較高的準(zhǔn)確性.結(jié)果表明，剪切變形不僅會(huì)影響彎曲振動(dòng)，對(duì)軸向振動(dòng)也有影響.

2）對(duì)于簡(jiǎn)支功能梯度梁，截面變化系數(shù)α 和梯度指數(shù)k 的增加會(huì)使得其固有頻率和臨界荷載減小，另外，截面變化系數(shù)對(duì)振型函數(shù)也有一定影響，但大致形狀不會(huì)改變.

3）可以通過(guò)改變邊界約束彈簧的剛度來(lái)實(shí)現(xiàn)經(jīng)典邊界條件下梁的固有頻率求解.