一種面向管道堵塞不均衡樣本集的主動學習方法

王顯龍 馮 早 趙燕鋒

（昆明理工大學a.信息工程與自動化學院；b.云南省人工智能重點實驗室）

隨著城市建設的快速發展，排水系統成為城市生態物質循環代謝系統的重要一環，正常運行的排水系統起到保護城市環境、提高居民健康水平以及維持城市交通正常運轉的作用［1］。近年來，城市內澇災害頻發，排水系統堵塞故障檢測的重要性也日益凸顯［2］。

因為聲波不僅能在空氣中傳播，還能在固體、液體和氣體介質中傳播，所以聲波作為一種無損檢測技術檢測排水管道的堵塞故障具有獨特優勢［3］。利用統計學習方法，對管道內的聲波信號進行有效預處理和特征提取，便可實現對管道運行狀態的識別。

隨著大數據和人工智能技術的發展，機器學習在故障診斷領域的應用越來越廣泛，目前基于數據驅動的管道故障識別大多采用監督學習方法。焦敬品等采用BP神經網絡對管道泄漏聲發射信號進行識別，整體識別率達到了92.5%［4］。伍林峰等采用小波包稀疏表征分類方法對管道堵塞情況進行識別，獲得了96.88%的準確率［5］。郎憲明等采用K均值欠采樣方法處理不均衡管道數據集，結合改進的雙支持向量機快速識別管道泄漏孔徑并定位泄漏位置［6］。然而，基于監督學習方法的管道檢測識別模型需要大量的已標注數據樣本訓練模型，這定會增加管道檢測數據樣本的標注成本。為此，僅在標注少量管道數據樣本的情況下，訓練高效且泛化能力強的管道堵塞識別分類模型至關重要。此外，排水管道的正常數據樣本量和堵塞數據樣本量存在嚴重的數據不均衡問題，若以傳統的監督學習方法分類識別模型，會造成嚴重的堵塞故障的漏診和誤判。

主動學習通過從未標注樣本集中挑選信息度高的樣本，經標注后補充到訓練集中，從而提升分類模型的性能［7］。為了篩選未標注樣本，Tong S和Koller D用不確定性度量的采樣策略篩選最靠近分類邊界的樣本［8］；陳念和唐振民采用QBC委員會的樣本采樣策略的主動學習模型對垃圾郵件進行在線過濾，降低了標注成本和時間成本，但是該方法并沒有考慮數據不均衡對分類結果的影響［9］；毛蔚軒等用基于經驗風險最小化的主動學習方法對惡意代碼進行檢測，實現了5.55%的低錯誤率，但是該方法嚴重依賴網絡數據，不具有通用性［10］。

筆者針對排水管道堵塞數據集中存在的嚴重的數據不均衡現象，提出基于分類熵和余弦相似度的樣本采樣策略和極限隨機樹的主動學習堵塞故障識別方法。

1 聲波信號檢測管道堵塞原理

管道中傳播的聲波，其特點是聲波被約束在管道里，沒有擴散，可以傳播得很遠［11］。在管道內部，聲波遇到堵塞物被反射回來，使得管內聲場形成駐波聲場。設Pi為入射檢測聲波聲壓，則有：

式中 c0——聲波的傳播速度；

k——波數；

P0——聲源振動產生的入射聲波聲壓；

t——聲波傳播時間；

x″——聲波傳播距離；

ω——聲源簡諧振動的圓頻率。

設堵塞物的聲壓反射系數為r，則反射聲波聲壓Pr的數學表達式為：

如果聲波在含有旁支的管道中傳播，由于旁支口的影響，主管道中將產生反射波，旁支管道產生漏入波，入射波有可能穿過旁支口產生透射波。

根據聲壓連續條件，可得反射波、入射波、漏入波和透射波之間的聲壓關系式為：

式中 Pb——漏入波聲壓；

Pt——透射波聲壓。

如圖1所示，聲波在管道內傳播，由于振動的空氣質點之間的摩擦，使得一小部分聲能轉化為熱能，稱為空氣對聲能的吸收。聲波遇到堵塞物，堵塞物吸收部分聲能。部分聲波繞過堵塞物發生衍射，這部分聲能穿過堵塞物傳遞到堵塞物的另一端。基于以上現象，只要檢測聲場相關物理量的變化就可以實現對管道運行狀況的識別。

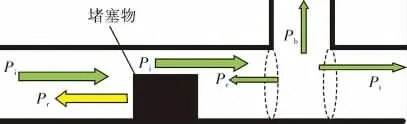
圖1 聲波在管道內的傳播示意圖

2 變分模態分解與特征提取

2.1 變分模態分解

傳統的傅里葉分析用一系列三角基函數對信號進行正交運算，但是管道內部情況復雜，采集到的往往是非線性、非平穩信號。若以傅里葉分析信號，得到的只是某一段時間內頻率的均值，無法準確描述頻率隨時間的變化［12］。雖然希爾伯特-黃變換能夠自適應地處理非平穩隨機信號［13］，但 是 經 驗 模 態 分 解（Empirical Mode Decomposition，EMD）方法存在不能分解低能量模態和產生虛假模態分量的明顯缺陷［14］。變分模態分解（Variational Mode Decomposition，VMD）是一種自適應、完全非遞歸的模態變分和信號處理方法，該方法克服了EMD方法存在端點效應和模態分量混疊的問題，并且具有更堅實的數學理論基礎，可以降低復雜度高和非線性強的時間序列的非平穩性，分解獲得包含多個不同頻率尺度且相對平穩的子序列，適用于非平穩性序列［15］。VMD的優點在于它能夠根據實際情況確定所給序列的模態分解個數，在隨后的搜索和求解過程中可以自適應地匹配每種模態的最佳中心頻率和有限帶寬，并且可以實現固有模態分量（IMF）的有效分離和信號的頻域劃分，進而得到給定信號的有效分解成分，最終獲得變分問題的最優解。VMD首先構建和求解變分問題，假設原始信號f（t）被分解為N個量，保證分解序列是具有中心頻率的有限帶寬的模態分量，同時各模態的估計帶寬之和最小，約束條件為所有模態之和并與原始信號相等，相應的約束變分表達式為：

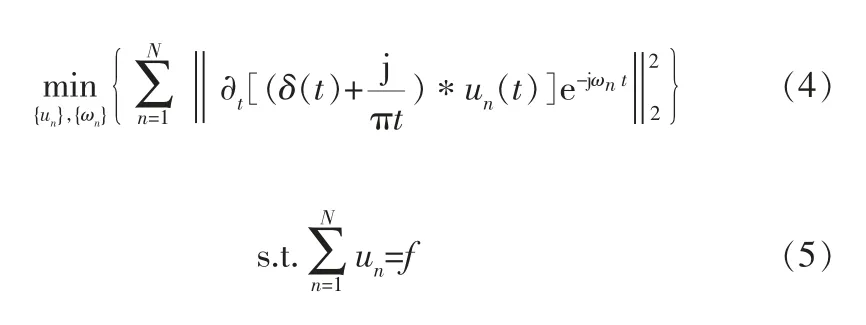
其中，N為指定分解的模態分量個數，*表示卷積運算，un、ωn分別為第n個模態分量和中心頻率。

為了降低噪聲干擾并求解式（5），引入拉格朗日算子λ和二次懲罰因子α，得到增廣拉格朗日表達式：

利用交替方向乘子 （Alternating Direction Method of Multipliers，ADMM）迭代算法、傅里葉等距變換優化得到各模態的分量和中心頻率，并搜尋增廣拉格朗日表達式（5）的鞍點，交替尋優迭代后分別更新un、ωn和λ：

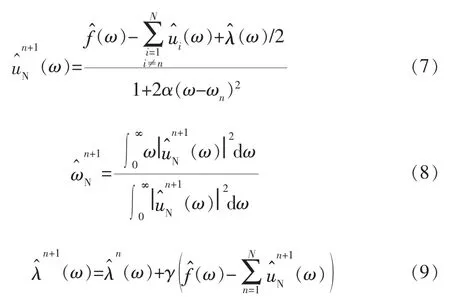
2.2 特征提取

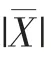
模糊熵的大小衡量了時間序列信號復雜度的大小，其計算步驟如下：

a.假設一個時間序列X（i），i=1，2，…，n′；

b.以m為窗，將時間序列X（i）分為k′=n′-m+1個序列，Xi（t）=（Xi（t），Xi+1（t），…，Xi+m-1（t））；

c.計算每個序列與所有k′個序列之間的距離d，并列表dij=max｜Xi+k′（t）-Xj+k′（t）｜，其中k′=0，1，…，m-1；

e.將窗m增長為m+1，重復步驟b～d；

f.計算模糊熵FuzzyEn（t）=lnφm（t）-lnφm+1（t）。

3 基于主動學習模型的管道堵塞故障識別

大多數的監督機器學習模型都需要基于大量數據的訓練才能取得良好的效果，尤其是帶有“標注”的數據，是監督模型的關鍵，制約著監督模型的學習效果。大多數情況下，相關領域專家獲得的是一個龐大的、未經標注的數據集。然而，數據的標注工作費時費力且成本高昂。為了盡可能地減少訓練集和標注成本，主動學習在機器學習領域應運而生。主動學習可以主動地提出數據標注請求，將一些經過篩選的數據提交專家進行標注，篩選數據的依據是數據的信息度。如圖2所示，主動學習過程分為兩個階段：

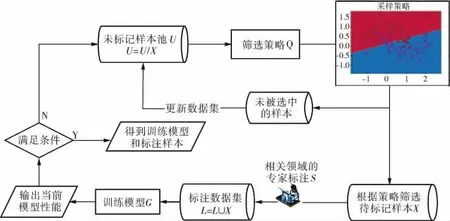
圖2 主動學習過程

a.初始化階段。從未標注的樣本中隨機選取小部分數據，由督導者標注作為訓練集L，剩余未標注樣本集為U，建立初始分類模型。

b.循環查詢階段。從未標注樣本集中按照查詢策略Q選取一定數量的樣本進行標注，并更新已標注樣本集L和未標注樣本集U，重新訓練分類器直至達到訓練停止標準為止。

3.1 基于分類熵和余弦相似度的樣本查詢策略

樣本信息指的是在訓練數據集中每個樣本帶給模型訓練的信息是不同的，即每個樣本為模型的訓練的貢獻是有差異的。從未標注樣本中集中篩選樣本，衡量樣本信息量差異的方法主要有不確定性標準、版本空間縮減標準和泛化誤差縮減標準［17］。為了度量模型對未標注樣本分類的確定性，引入熵的概念，熵可視為系統中無序性的度量。如果模型對給定數據點的類別具有高度的確定性，則對于特定類可能具有較高的確定性，而所有其他類的可能性都比較低。在高熵的情況下，意味著該模型將概率近似地分配給所有類別，因為模型根本不確定該數據點屬于哪個類別，這與使氣體均勻分布在盒子的所有區域的情況相似。因此，具有較高熵的數據點較具有較低熵的數據點應該有更高的優先級被篩選出來提交人工標注。分類熵SE的定義如下：

使用分類熵（或其他類似策略）抽樣時，無法考慮數據的結構分布信息，這將導致進入次優查詢。為了緩解這種情況，一種方法是使用信息密度度量幫助指導查詢。余弦相似性通過測量兩個向量的夾角的余弦值來度量它們之間的相似性。從樣本集U中，采用樣本篩選策略構建待標注的數據集Xu，從中篩選的樣本x的信息密度I（x）可計算為：

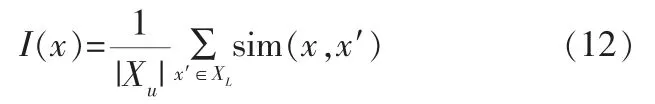
其中，x′表示已標注樣本。

在篩選樣本時，為了同時考慮樣本的不確定性和代表性，筆者選擇分類熵和余弦相似度相結合的方式求其最大值實現樣本查詢策略來篩選未標注樣本，即arg max（SE+I（x））。

3.2 基分類器——極限隨機樹

極限隨機樹算法與隨機森林算法十分相似，都是由許多決策樹構成的［18］。隨機森林的多個決策樹都是互相獨立的，并且不需要進行“剪枝”操作。在訓練過程中，每棵決策樹采用有放回采樣方法構造新的訓練數據集，在一個隨機子集內得到最佳分叉屬性。相較于傳統的集成學習方法，隨機森林能較好地容忍噪聲且穩定性較高。極限隨機樹應用的是Bagging模型，極限隨機樹使用的所有的樣本，只是特征是隨機選取的，其主要過程為：當特征屬性是類別的形式時，隨機選擇具有某些類別的樣本為左分支，而把具有其他類別的樣本作為右分支；當特征屬性是數值的形式時，隨機選擇一個處于該特征屬性的最大值和最小值之間的任意數，當樣本的該特征屬性值大于該值時作為左分支，當小于該值時作為右分支。這樣就實現了在該特征屬性下把樣本隨機分配到兩個分支上的目的。然后計算此時的分叉值，如果特征屬性是類別的形式，采用基尼指數；如果特征屬性是數值的形式，采用均方誤差。遍歷節點內的所有特征屬性，按上述方法得到所有特征屬性的分叉值，并選擇分叉值最大的形式實現對該節點的分叉。

綜上所述，極限隨機樹相較于隨機森林有兩個優點：首先極限隨機樹可以減少偏差；其次極限隨機樹中每棵決策樹的分裂閾值是完全隨機選擇的，可以減少方差。因此，筆者提出以極限隨機樹為基分類器，結合分類熵和余弦相似度的樣本查詢策略，建立主動學習模型，以實現對排水管道堵塞故障數據集在不均衡情況下的分類識別。

4 試驗方案設計與數據采集

為了模擬排水管道的運行情況，筆者設計了排水管道模擬試驗平臺（圖3），PVC排水管道的總長度為15.4m、管道的直徑1為50mm，管道分為3段，分別設置為空管區域、管道堵塞區域和管道三通件區域。循環水泵和水箱控制管內水位保持較低水位的流動。試驗平臺中的計算機安裝WinMLS軟件，并驅動聲卡產生時間為10s、頻率范圍100～6 000Hz的正弦掃頻信號作為檢測聲波信號，檢測聲波信號由揚聲器釋放到管道內部。由于揚聲器發出的不一定是純音，所以必須在接收端進行濾波，去除不必要的高次諧波分量。四通道傳聲器采集管道內部信號，傳聲器的采樣頻率設置為44 100Hz，經放大器放大后上傳至計算機做進一步處理。

圖3 排水管道模擬試驗平臺

管道堵塞程度設置與管道直徑的比例存在一定關系，定義堵塞物高度在管道直徑的1/3以下為輕度堵塞，堵塞物高度超過管道直徑的1/3為中重度堵塞。本試驗用20mm障礙物模擬輕度堵塞，55mm障礙物模擬中重度堵塞。試驗采集無堵塞直管、輕度堵塞、中重度堵塞和含三通件正常管道4種管道運行狀態信號數據，時域信號如圖4所示。為了模擬管道堵塞故障類別不均衡程度，試驗方案設置兩組數據的類別數量比例分別置為1.0∶1.0∶0.3∶0.2和1.0∶1.0∶0.2∶0.1，兩組數據分別模擬不同的數據不均衡程度，第1組數據和第2組數據的總數分別為250和210。

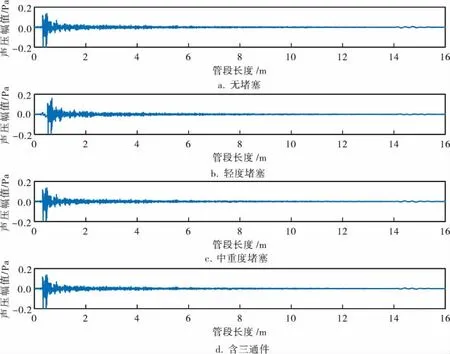
圖4 4種管道運行工況下的時域信號

為了提取信號的有效特征表征不同的類型數據，需要對采集到的時域信號進行特征提取。特征提取的主要過程是：先對信號進行變分模態分解，根據模態分量的中心頻率選擇分解個數為4［19］。以無堵塞直管運行狀態時域信號為例，其分解結果如圖5所示。

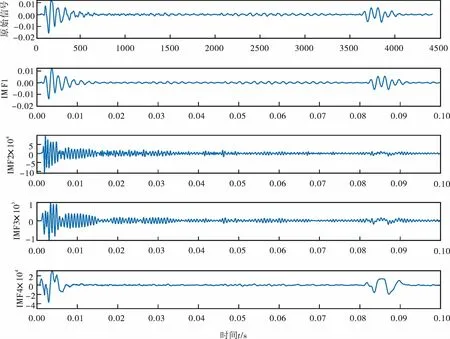
圖5 無堵塞直管時域信號變分模態分解結果

由于原始信號經由變分模態分解后得到4個模態分量，分別計算這4個模態分量的脈沖因子和模糊熵，其中模糊熵嵌入維數越大時越能更細致地重構系統的動態演化過程，本試驗選取嵌入維數為4［19］。信號的最終特征提取結果見表1、2。

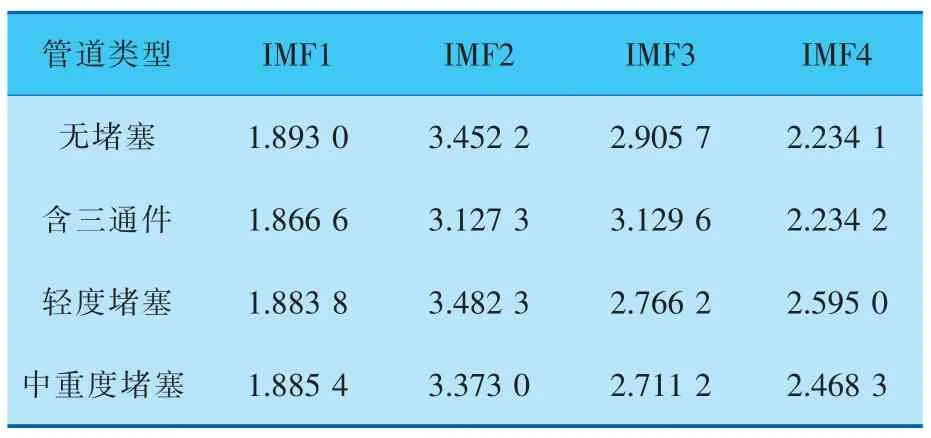
表1 脈沖因子特征提取結果

5 試驗與分析

為了驗證基于極限隨機樹的主動學習模型對排水管道堵塞故障識別的有效性，基于試驗平臺選取兩組試驗數據。根據故障類數據所占總數據的比例，定義數據集一為普通不均衡數據集，數據集二為極端不均衡數據集。設置兩組數據集的不均衡比例變換主要是為了檢測主動學習方法的有效性。初始已標注訓練集為12個樣本，各類別的樣本個數分別為4、4、2、2，主動學習過程中，樣本查詢次數均為20次。

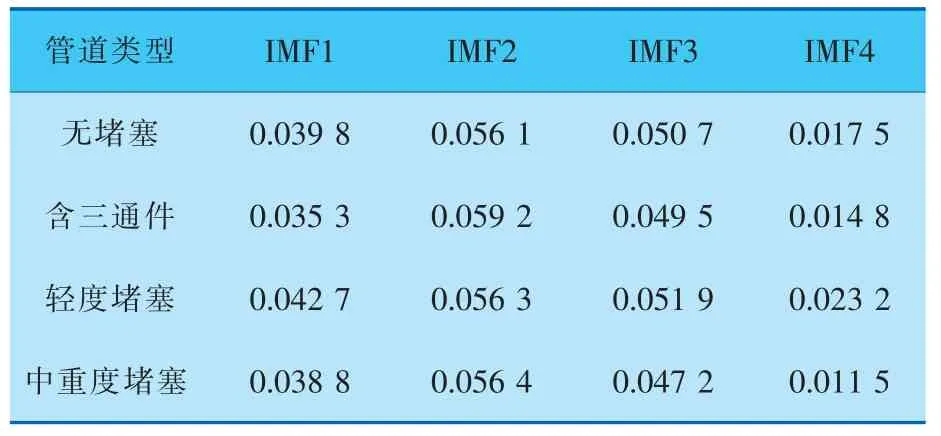
表2 模糊熵特征提取結果

為了檢驗基于極限隨機樹的主動學習模型對管道堵塞故障的識別能力，通過繪制模型的學習曲線和混淆矩陣進行比較。排水管道堵塞識別主動學習模型如圖6所示，首先在信號采集完成之后利用已標注樣本訓練集訓練排水管道堵塞故障分類識別模型——極限隨機樹，然后在已有分類模型的基礎上使用分類器評價剩余未標注樣本并對選擇出的待標注信號進行樣本標注，其次更新已標注的訓練集和未標注的訓練集，如果分類模型的輸出精度符合要求則停止迭代訓練過程并輸出最終結果。

圖6 排水管道堵塞識別主動學習模型

5.1 初始分類模型對未標注樣本集測試結果的分析

筆者所提分類模型對數據集一的初始識別結果如圖7所示，可以看出，在相同大小的已標注訓練集下得到的模型，在普通不均衡數據集下得到的測試準確率略高于在極端不均衡數據集下的測試準確率。

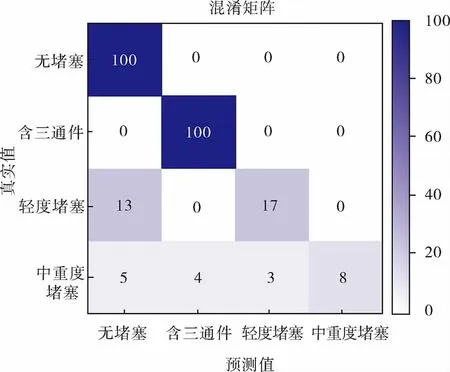
圖7 分類模型對數據集一的初始識別結果

本試驗中，由于管道堵塞故障數據集是不均衡的，對數據集分類識別時更應該看重少數類數據樣本的分類結果。因此，筆者選擇混淆矩陣來判斷模型對少數類樣本的識別效果。分類模型對數據集二的初始識別結果如圖8所示，可以看出，在進行未標注樣本采樣之前，由于訓練樣本較少，在普通不均衡數據集上，模型對少數類堵塞故障樣本的分類識別準確率不理想，隨著堵塞故障的少數類樣本進一步減少，模型在極端不均衡數據集中，對堵塞故障的識別效果進一步降低，出現了對中重度堵塞故障全部識別錯誤的情況。這是因為一般分類模型在對少數類樣本進行分類識別時，往往以最小經驗風險為優化原則，忽視了少數類樣本。在對未標注樣本集進行篩選采樣之前，雖然模型對管道運行狀態的識別均達到了90%以上的正確率，但是把堵塞類故障判別為正常類管道樣本會造成更加嚴重的后果。為了避免主動學習過程對少數類樣本的錯誤分類，從未標注樣本集中選取樣本進行標注，是提高堵塞故障少數類樣本識別準確率的關鍵。

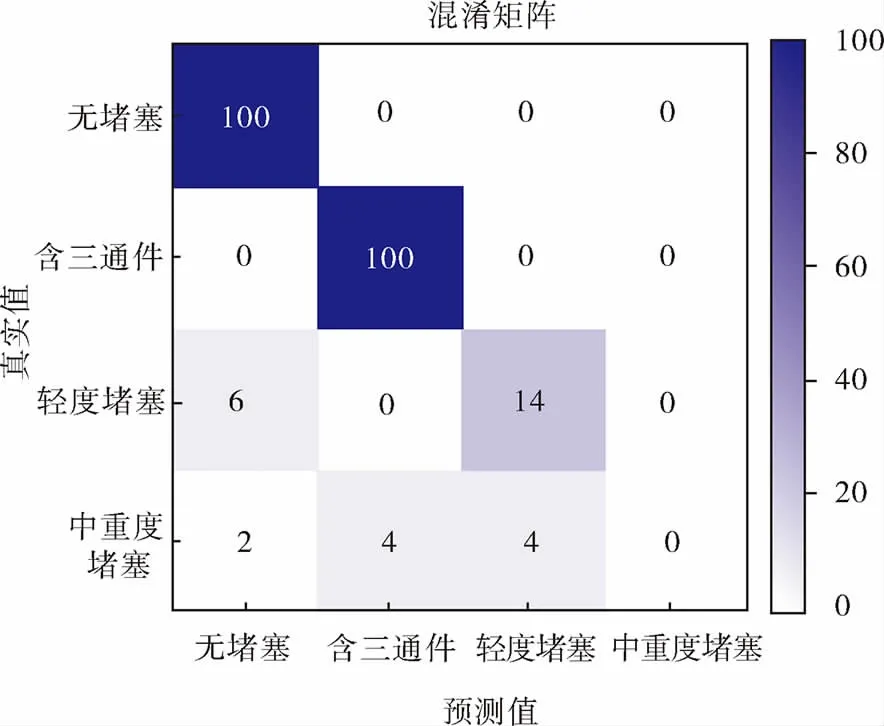
圖8 分類模型對數據集二的初始識別結果

5.2 主動學習模型分類性能分析

主動學習模型在兩個數據集的學習曲線如圖9所示，可以看出，筆者提出的方法在普通不均衡數據集和極端不均衡數據集上分別取得了97.6%、97.8%的準確率，即使數據集中的不平衡比例增大，也沒有影響筆者所提方法的準確率。

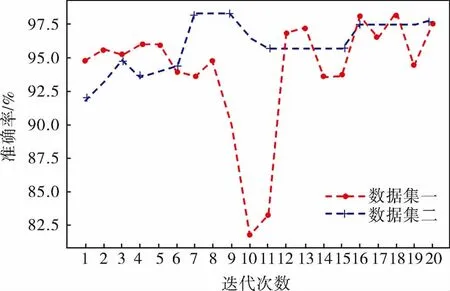
圖9 主動學習模型在兩個數據集的學習曲線

本試驗的樣本篩選策略主要考慮了分類模型對已篩選待標注樣本的分類不確定性。同時，為了避免少數類樣本對分類結果造成影響，通過余弦距離計算待標注樣本與已標注樣本集中各類別樣本的特征距離，以衡量樣本之間的相似程度，這在很大程度上改善了分類器對標注樣本集中少數類別樣本的誤判。

分類模型在普通不均衡數據集的最終識別結果如圖10所示，可以看出，數據集一的最終分類結果與模型初始分類結果相比，經過20次的未標注樣本迭代查詢后輕度堵塞中有3個樣本被誤分類為無堵塞管道，中重度堵塞類樣本中有1個樣本被誤分類為無堵塞管道，2個中重度堵塞樣本被誤分類為含三通件管道。

分類模型在極端不均衡數據集的最終識別結果如圖11所示，可以看出，數據集二的最終分類結果與模型初始分類結果相比，輕度堵塞類別樣本中僅有5個樣本被誤分類為無堵塞管道，中重度堵塞樣本全部分類識別正確。

圖10 分類模型在普通不均衡數據集的最終識別結果

5.3 查準率、查全率和F1度量值分析

根據圖10、11可以得到筆者所提模型在普通不均衡數據集和極端不均衡數據集上的分類指標查準率P、查全率R和F1度量值。其中F1度量值由查準率和查全率計算得到，即：

其中，β為可調參數，通常取1。

可以看出，F1度量值與查準率P、查全率R成正比，F1度量值越大說明分類模型對少數類的分類效果越好。

根據圖10、11可以得到筆者所提主動學習模型在普通不均衡數據集和極端不均衡數據集上的分類指標，結果見表3、4。可以看出，主動學習模型對中重度堵塞少數類樣本的識別效果有了很大的改進。但相對于中重度堵塞，樣本數量較大的輕度堵塞的F1度量值降低了，經分析，造成該后果的原因可能是在減少輕度堵塞樣本的數據量時破壞了原始樣本分布信息。

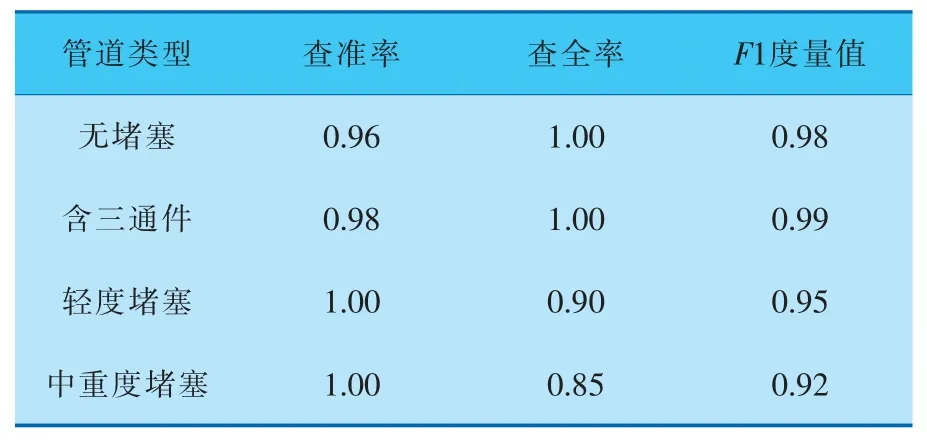
表3 普通不均衡數據集的分類指標

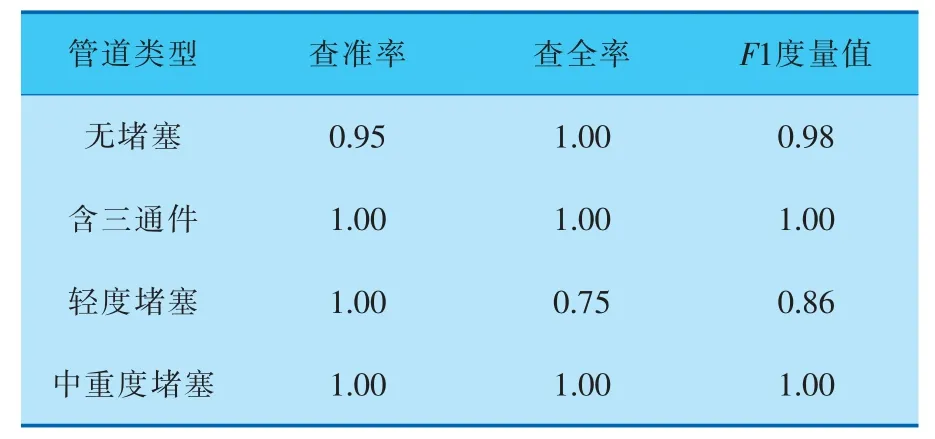
表4 極端不均衡數據集的分類指標

6 結束語

為了在排水管道堵塞故障檢測過程中減少人工標注的負擔，筆者提出了基于主動學習的排水管道堵塞故障識別模型。同時考慮到數據不均衡對分類結果造成的影響，改進了在主動學習過程中的樣本查詢策略。為了避免主動學習過程中數據不均衡給分類結果造成的不良影響，提出將衡量樣本分類不確定性的分類熵和樣本分布信息的余弦相似度相結合的樣本查詢策略，該策略在樣本查詢選擇過程中考慮了未標注樣本集中的少數類樣本。試驗在兩組不均衡比例不同的數據集進行驗證：在樣本標注成本上，本試驗以僅標注32個樣本的標注成本在兩個不均衡比例不同的數據集進行識別驗證，均取得了較好的準確率，并極大地節省了人工標注樣本的成本，而且筆者提出的主動學習模型能夠顯著提高少數類樣本的F1度量值。

由于本試驗考慮的試驗條件是基于一個堵塞物，而在實際管道檢測條件下，排水管道內部情況很復雜，大多數情況下會出現多重堵塞的管道，有些更加復雜的管道堵塞樣本的數量更為稀少，因此，筆者提出的方法在更為極端的數據不均衡情況下還需更近一步驗證。