多策略混合搜索的變時段人工蜂群算法及應用

楊舟，劉招*，呂嘉瑋，雷曉輝

(1.長安大學水利與環境學院，西安710054；2.長安大學旱區地下水文與生態效應教育部重點實驗室，西安710054；3.中國能源建設集團山西省電力勘測設計院有限公司，

太原030000；4.中國水利水電科學研究院，北京100000）

0 引言

【研究意義】水庫優化調度模型具有高維度、多約束、非線性等特點，解決這些問題的核心是建立能準確反映實際優化調度問題的模型并采用適當的求解方法[1]。對水庫洪水調度而言，其模型特點不盡相同。洪水過程多為流量變化劇烈持續時間較短，若采用超過6 h 的流量系列無法準確反映流量變化，故洪水調度多關注次洪或汛期，模型采用的時段步長較小，一般以1、3 h 或6 h 等[2-5]多見；而發電調度更注重機組持續出力，除考慮廠內經濟運行外，時段步長多見日、旬或月等。故已有的防洪發電雙目標優化問題一般也主要針對汛期或次洪，采用較小時段步長進行優化計算，化解了2 種調度模型時段不一致問題。然而，若考慮在較長系列上建立發電和防洪的雙優化模型，這樣的處理顯然很不合理。一方面是因為數據可能不支持，無法獲取小時時段的流量數據；另一方面，對歷時更長的非汛期，流量變化不大，采用小時段也沒有必要。在此情形下，對于有非汛期洪水、以中小洪水作為重要水資源或水資源利用率較高的水庫，如何通過建立合理的變時段步長優化模型，并獲取較高精度的求解結果十分有意義。然而，有關這一問題多年來給出的解答很少[6-7]。

【研究進展】多年來，有關水庫優化調度問題已有大量研究，相關理論方法日臻成熟，但是優化準則眾多[7-13]，所以在選擇優化方法時，應根據水庫的具體情況分析選用。人工蜂群算法（Artificial Bee Colony Algorithm，ABC）自2001 年[14]首次提出后就被廣泛應用于求解水庫優化調度問題[15-17]，基本的人工蜂群算法具有前期收斂速度快、高穩定性、高效率、魯棒性強等優點。【切入點】但是其整體收斂速度慢[18]、開發能力不足[19]的缺陷還有待提升。在國內外部分學者提出的單一改進搜索策略[20-22]基礎上，Kiran 等[23]提出了ABCVSS 算法、Lin 等[24]提出了ABCLGII 算法、Xiang 等[25]提出了ABGG 算法等多搜索策略的改進算法，一定程度提升了ABC 算法的探索能力；劉琨等[26]提出了基于加強局部搜索策略的人工蜂群算法，宋曉宇[27]提出了多策略混合搜索人工蜂群算法（Artificial bee colony algorithm based on multi-strategy hybrid search，MHABC），并運用文獻[28]中定義的函數測試集進行測試，結果證明多策略混合搜索人工蜂群算法較好地彌補了ABC 算法收斂速度慢、開發能力不足的缺憾。【擬解決的關鍵問題】因此，本研究采用多策略混合搜索人工蜂群算法結合變時段步長特性，以具體水文案例進行研究分析。

1 材料與方法

1.1 研究方法

鑒于標準ABC 算法國內外眾多學者已對其進行了大量的研究分析，本研究不再對其步驟進行詳細說明[29-30]，僅介紹改進的搜索策略和時段步長變化公式。標準ABC 算法搜索策略為：

式中：xi≠xk，xk為種群中隨機個體；?i,j為[-1,1]間隨機數。

1）雇傭蜂階段，搜索策略替換為高斯分布的搜索策略，命名為SABC1（Artificial bee colony algorithm search strategy），計算式為：

式 中：xr1≠xr2≠xi，xr1,xr2為 種 群 中 隨 機 個 體；?i,j～N(0,0.4)，為高斯分布隨機數，較均勻分布隨機數有更集中的搜索區域，易于算法收斂。SABC1 能很好提升單峰函數收斂速度，卻容易在多峰函數求解過程中陷入局部最優。因此，提出SABC2 如下：

xr1≠xr2≠xr3≠xr4≠xi，xr1,xr2,xr3,xr4為種群中隨機個體；μi,j服從均勻分布[-1,1]，φi,j～N(0,0.3)，為高斯分布隨機數，種群個體和分布參數的隨機性使算法的探索能力得到保障。第三項的引入為搜索步長提供更多可能，高斯分布參數通過調控xr3,xr4步長，使其有高概率集中于（-0.3,0.3）之間，小步長可以有效減少錯過最優解概率；同時，分布在（-0.3,0.3）之外的取值加快收斂。三項式通過SN(SN-1)(SN-2)(SN-3)的步長組合保證了種群多樣性，增加了步長方向的可選擇性，使算法兼具探索能力與開發能力。

2）通過在觀察蜂階段引入精英解以增強算法開發能力與探索能力，計算式為：

式中：xelite,j為種群前10%個體中隨機選擇的精英個體，其他參數同式（1）或式（2）。觀察蜂階段以精英解作為搜索起點，可以有效促進種群收斂速度，從而增強開發能力。

3）為保證4 個搜索策略都能有效發揮，需在雇傭蜂與觀察蜂階段均運用混合搜索機制，經過作者充分實驗，得出二項式搜索策略被分配60%的使用機會，三項式搜索策略被分配40%的使用機會為最佳比例。

4）段步長變化公式，計算式為：

式中：hi、di分別入庫流量時間序列中對應的d 和h；?Ti為相鄰時段步長（h）。

1.2 優化調度模型的建立

1.2.1 目標函數

在滿足水庫防洪、發電、航運、灌溉等約束條件的前提下，以發電量最大作為主要目標函數。即：

式中：E為非汛期最大發電量（kW·h）；η出力系數，無量綱；Qi為發電流量（m3/s）；Hi為發電水頭（m）；Ti為上文中變時段步長。

1.2.2 約束條件

優化調度模型的約束條件如下：

1）水庫水量平衡約束：

式中：Vi為水庫時段i的水庫蓄水量（m3）；Qi,qi分別為水庫i時段的入庫流量、出庫流量（m3/s）；Ti為上文中變時段步長。

2）水庫水位約束：

式中：ZMIN、ZMAX分別為水庫i時段的最低限制水位、最高限制水位（m）；水庫水位對應水庫庫容（m3），二者為等價約束。

3）出力約束：

式中：NMIN為保證出力、NMAX為預想出力（kW）。由于水庫的發電量與機組的出力相對應，而優化算法中的適應值又表示水庫的總發電量。所以對出力約束的處理應該直接考慮在最終的適應度函數中[30]。用Bi表示第i個時段出力的違約情況，表示正常出力的計算值（kW），則Bi為：

實施約束限制后總電量為：

式中：E*為無出力約束下的發電量計算值（kW·h）；PN為對出力約束的懲罰力度系數，無量綱。

由式（12）可知，在原始發電量一定的情況下，出力的違約次數越多，針對其懲罰的力度越大，實際效益越少，從而確保算法向違約數目較少的方案收斂。

4）出庫流量約束：

式中：QMIN為最小出庫流量（m3/s），應大于灌溉要求；QMAX為水庫允許的最大出庫流量（m3/s）。流量約束的處理方式和出力約束處理的方式相同，都是采用罰函數的方法。

5）各變量非負約束

1.2.3 算法流程

步驟1：初始種群產生。

步驟2：雇傭蜂搜尋蜜源，計算蜜源適應度，保存較優值；此過程中，生成[0,1]隨機數rt，若rt<0.6，采用SABC1 作為搜索策略，反之采用SABC2 作為搜索策略。

步驟3：觀察蜂根據輪盤賭的方式選擇雇傭蜂，并在雇傭蜂附近搜尋新的蜜源并計算適應度，與雇傭蜂的蜜源適應度相比較，由貪婪法選擇較優值；此過程引入精英解，同時生成[0,1]隨機數rt，若rt<0.6，采用式（4）作為搜索策略，反之采用式（5）作為搜索策略。

步驟4：若有被拋棄的蜜源，則雇傭蜂轉化為偵查蜂，重新尋找新蜜源并與步驟3 的值進行比較優選，如果小于步驟3 的值，則繼續搜索，否則執行步驟5。

步驟5：如果迭代次數未達到1000 次，則轉到步驟2；否則輸出最優解。

1.2.4 算法參數設置

維度由水庫實測流量的時段數決定，種群數量100，蜜源SN=50[31]；為提高模擬精度，給予算法較大約束，設置罰函數為106；標準ABC 算法在多次模擬中，最慢收斂速度不超過950 代，為保證模擬結果的有效性，設置最大迭代次數1000 次。此外，與標準ABC 算法相同工況條件作為對比。

2 結果與分析

2.1 數據來源

萬安水庫自建成以來運用并未達到設計要求，一直按初期運用水位蓄水運行，水庫防洪、灌溉、發電等綜合利用效益未得到完全發揮。加之萬安水庫非汛期常有洪水發生，且在當前水庫未達到原設計的運用條件下，非汛期洪水對水庫發電等綜合效益有非常重要的影響。而非汛期水庫洪水調度的首要目標，即在確保大壩及下游地區防洪安全的前提下，使發電量達到最大。基于以上背景，本研究運用多策略混合搜索的變時段蜂群算法對萬安水庫的非汛期調度進行優化求解。萬安水庫具體參數指標：最大發電流量2 800 m3/s，滿足灌溉流量150 m3/s，裝機容量40 萬kW，保證出力4.7 萬kW，預想出力4.7 萬kW，額定水頭15 m，正常蓄水位96 m，汛限水位85 m。

在綜合考慮歷年水文資料的完整性、可行性的前提下，本研究選取了萬安水庫2006—2017 年的水文資料作為計算數據。通過10 次運算得出標準ABC 與MHABC 優化調度下的總發電量及各約束條件變化情況，發電量取平均值。

2.2 計算分析

水庫優化調度的前提是保證水庫自身和下游防洪安全，同時盡可能提升洪水資源的利用，洪水調度結束時，預留較多的防洪庫容可以更為靈活地應對后續洪水；在枯水期，水庫下泄流量應滿足下游灌溉、通航。因此，綜合以上要求，本研究以灌溉保證率、水庫安全保證率、防洪保證率、庫容預留率、發電提升率組成綜合評價體系，評價各約束條件滿足情況以及調度的綜合效益。其中，灌溉保證率、水庫安全保證率、防洪保證率分別表示下泄流量大于等于150 m3/s、水庫水位不超過96 m、下泄流量不超過8 800 m3/s 的時段占總調度時段的比例。各指標滿足情況見表1。

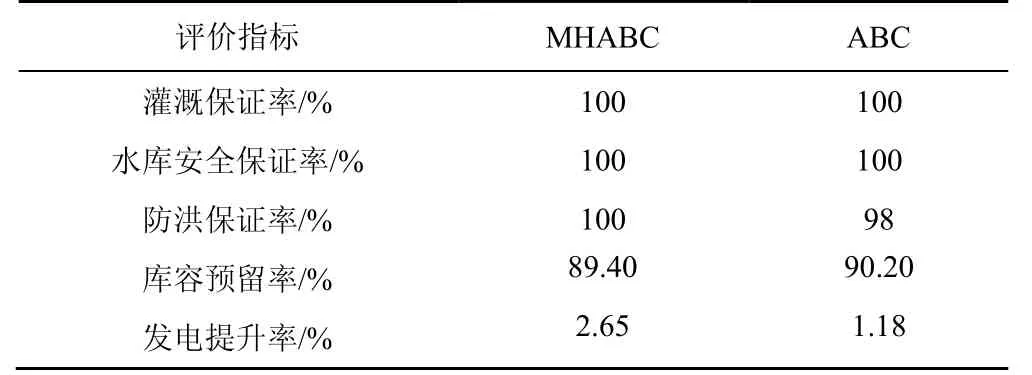
表1 各指標滿足情況Table 1The satisfaction chart of each index

由表1 可知，2 種優化調度模型均能很好滿足防洪、灌溉等約束條件，在保證自身安全的前提下，有效提升了綜合效益。但MHABC 模型的發電提升率、防洪保證率分別高出標準ABC 模型1.47%、2.00%，只是在庫容預留率較后者少了0.8%。通過以上5 個指標可以看出，基于MHABC、標準ABC 所建立的變時段優化調度模型均可以很好的完成萬安水庫非汛期的優化調度，且MHABC 的綜合效益更高。

鑒于2015 年非汛期發生多場洪水且來水較大，將MHABC 調度結果入庫流量、出庫流量、發電流量、水頭差的變化情況繪制成圖，結合水庫多年水量利用率進行分析。入庫、出庫、發電流量、水頭變化情況圖和多年實際調度與優化調度水量利用率對比分別見圖1、表2。

表2 實際調度與優化調度水量利用率對比Table2 Comparison table of water utilization ratio between actual dispatching and optimal dispatching

由圖1 可知，在來水低于2 800 m3/s 時，水庫出入庫流量曲線基本吻合；當入庫流量超過2 800 m3/s且低于8 800 m3/s 時，出庫流量較入庫流量稍低，避免了出庫流量過大，減少了不必要的棄水；當入庫流量超過8 800 m3/s 時，為防洪需要，出庫流量不會超過8 800 m3/s，同時在退水階段增大下泄，且下泄流量不超過最大發電流量，使洪水資源得到充分利用。此外，優化調度中上下游水頭基本控制在24～28 m，且發電流量小時、水頭差大，機組持續高效出力，年發電量得以提升。由表2 可知，優化調度較實際調度多年水量利用率增大了2.8%，且增幅主要發生在有大洪水的年份，如2011、2012、2015 年，佐證了MHABC 模型在優化調度中提高了洪水資源的利用效能。

為驗證MHABC 模型較標準ABC 模型的收斂性更優，選取兩者最大適應度不同區間段年份的尋優成果，將其適應度曲線與迭代次數關系見圖2。

由圖2 可知，MHABC 模型的迭代次數在100 以前，各年份適應度函數均迅速增大，至多在200 左右便完成收斂，尋到最優值；除2011 年外，標準ABC模型下其余年份的迭代次數在100 之后都進入了緩慢的增長期，個別年份甚至在600 以后才能保持基本穩定，雖然2011 年做到了整體的快速收斂，但是標準ABC 算法所建立模型的收斂性具有隨機性，不能做到普遍的高收斂，適應性較MHABC 偏弱。

3 討論

3.1 算法的創新性

基于MHABC 的變時段人工蜂群算法較標準ABC 算法能更好地解決復雜洪水序列的優化調度問題，在提高了綜合效益的同時，還具備更高效的全局收斂速度，這些提升得益于MHABC 所采用的二、三項式混合使用的搜索策略以及精英解的提出。二、三項式的分配使用增加了算法的探索能力，二項式可以輕易解決單峰函數的優化問題，三項式能避免在求解多峰函數時陷入局部最優，二者配合使用相得益彰；精英解的提出，提高了尋優的起點，使得函數更快向全局最優解靠近，從而加快了全局尋優速度。MHABC算法結合變時段特性，在滿足多約束條件的前提下，加大了對洪水資源的開發利用，做到了對非汛期洪水、中小洪水調度的融合優化。

3.2 萬安水庫調度科學性評價及建議

鑒于現實中水庫來水的不確定性，優化調度目前只能應用于對以往調度的科學性進行評價，優化結果更多的是為未來調度輔以參考。因此，本研究認為，萬安水庫多年非汛期總體調度較為優異，在保證水庫及下游防洪安全的同時，入庫流量轉換成經濟效益的成果極其顯著。需要提升的有：

1）加強對洪水資源的利用，即洪水期減少不必要的棄水，且在退水期間盡可能做到下泄不超過最大發電流量，做到達到機組滿發的同時又不影響水庫自身安全；

2）提升對上下游水頭的控制，保證上下游水頭不低于額定水頭是機組持續出力的有效手段。

4 結論

1）MHABC 模型下，水庫安全保證率、灌溉保證率、防洪保證率等多年均值均為100%，水庫預留庫容多年均值為89.4%，表明MHABC 模型構建的變時段優化算法很好地滿足了防洪、灌溉等約束條件。

2）通過對非汛期洪水的合理調控，提升了洪水資源利用率，多年水量利用率提升了3%。

3）MHABC 算法所采用的綜合搜索策略提高了標準ABC 算法的尋優效率和開發能力，緩解了多約束條件優化模擬計算時，時段步長選取與運算精度和收斂速度之間的矛盾。