區域大氣水汽轉換系數的一種新算法

謝劭峰, 李國弘, 周志浩, 趙 云, 張 偉

(桂林理工大學 a.測繪地理信息學院; b.廣西空間信息與測繪重點實驗室; 廣西 桂林 541006)

0 引 言

利用地基GNSS反演大氣可降水量(PWV)時, 水汽轉換系數Π是非常關鍵的參數。在實際應用中, 為了獲得PWV, 通常可以取Π值為常數0.15[1]或通過Bevis模型[2]、建立局部地區加權平均溫度(Tm)模型或建立Π值模型獲得。在建立Tm模型方面, 王勇等[3]利用武漢地區無線電探空資料構建武漢地區的Tm模型; 李國翠等[4]通過分析加權平均溫度與地面氣象要素的關系, 建立了華北地區Tm模型; Wang等[5]利用探空資料和歐洲中期天氣預報中心(ECMWF)再分析資料, 建立中國地區Tm模型; 姚宜斌等[6]根據加權平均溫度和函數內積的定義, 推導了Tm與Ts的非線性函數關系模型; 謝劭峰等[7]研究建立了基于地面溫度的廣西地區氣象參數Tm模型和基于GGOS格網Tm的新疆地區加權平均溫度精化模型[8]; 陳發德等[9]利用小波去噪方法對Tm進行改正, 在建立廣西Tm模型。建立Π值模型方面, Emardson等[10]提出直接利用測站緯度和年積日計算轉換系數Π值的方法; 姚朝龍等[11]利用中國低緯度地區20個探空站數據建立了區域性Π值模型(低緯度模型); 姚宜斌等[12]利用GGOS提供的大氣濕延遲(ZWD)和ECMWF提供的PWV格網數據建立了一種全球轉換系數Π值模型; 劉立龍等[13]利用探空站資料建立了廣西地區大氣水汽轉換Π值模型(廣西高程模型)。然而, 上述Π值計算方法或忽略了測站緯度，或受高程或(半)年周期的影響, 降低了其精度。

本文利用2015—2017年廣西4個探空站數據, 先通過探空站資料積分法解算出探空站點的加權平均溫度Tm, 利用Tm計算大氣水汽轉換系數Π, 通過分析Π的特性, 建立了直接反映年周期、半年周期、高程改正和緯度改正的廣西地區大氣水汽轉換系數的計算模型(本文模型), 并與低緯度模型、廣西高程模型進行了內、外符合精度以及PWV反演精度的對比。

1 轉換系數Π的計算

PWV與ZWD之間的關系可以表示為

PWV=Π·ZWD;

(1)

(2)

其中:ρw為液態水的密度;Rv為水汽氣體常數;k2′、k3為大氣折射常數;Tm為大氣加權平均溫度。

轉換系數Π還可以根據測站緯度和年積日按Emardson模型計算

(3)

式中:Π是對應年積日doy、緯度為φ的測站水汽轉換系數;a0為常數;a1為緯度φ的參數;a2、a3為年周期振幅。

此外,廣西地區Π還可以用低緯度模型[11](式(4))和廣西高程模型[13]進行計算(式(5))

(4)

(5)

相比于Emardson模型, 低緯度模型、廣西高程模型增加了測站高程改正。

2 廣西Π值分析與新模型建立

2.1 廣西Π值分析

為獲取精確的廣西地區Π值, 本文利用廣西百色站、梧州站、桂林站、南寧站4個探空站2015—2017年的探空站數據, 采用數值積分法先獲取精確的大氣加權平均溫度Tm, 再通過式(2)求取轉換系數Π值。對4個探空站資料進行上述分析計算并可獲得各站點2015—2017年的Π值隨時間變化情況(圖1)。

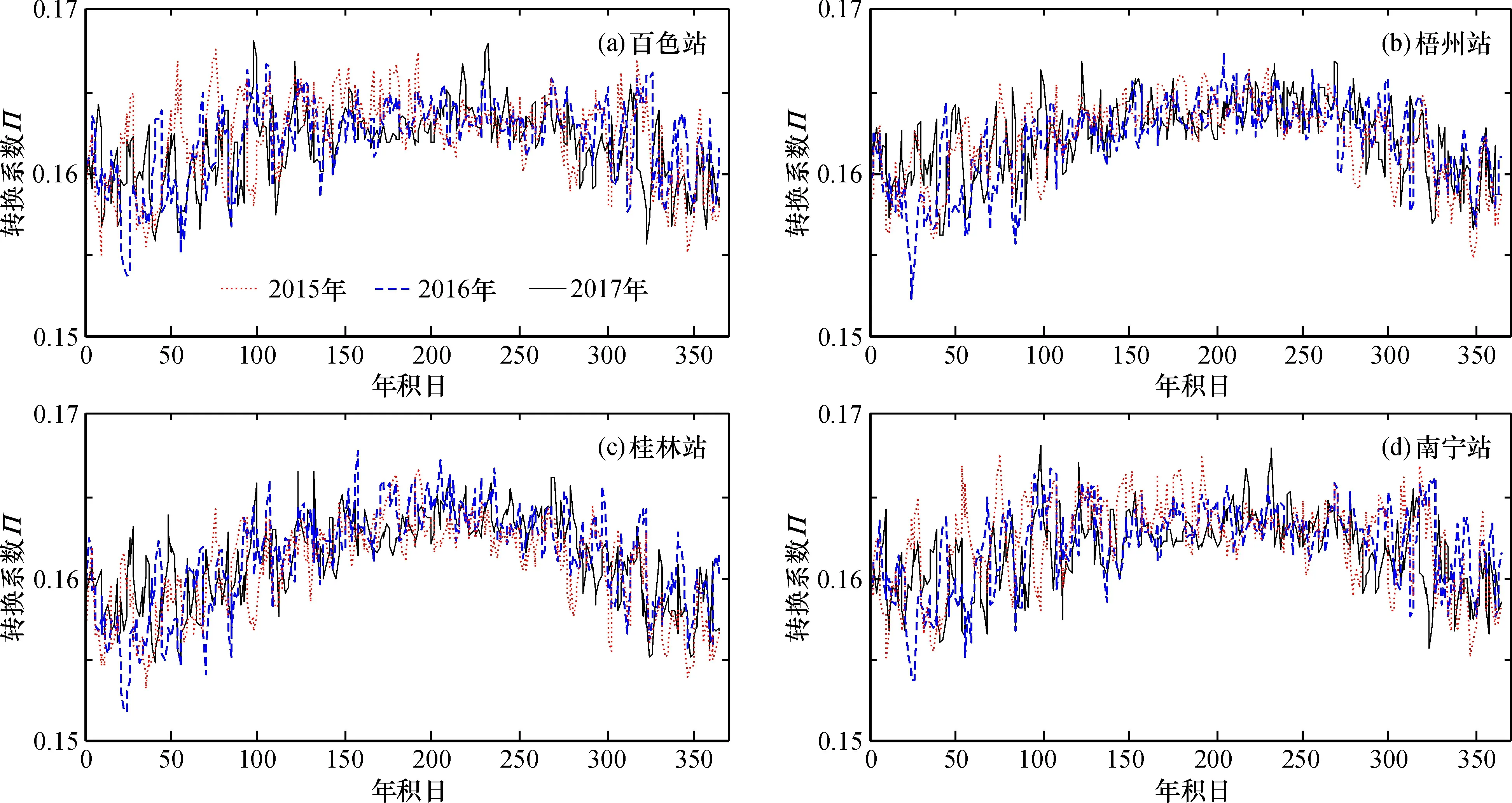
圖1 Π值的日變化特征Fig.1 Daily variation characteristics of Π

可知, 4個探空站點的Π值是隨時間變化的, 可見將Π值作為一個常數是不合適的。對比4個探空站3年Π值變化可知:Π值分布在0.15～0.17; 同一站點上3年Π值隨時間的變化趨勢一致; 不同站點Π值隨時間的變化趨勢一致; 4個站點Π值都存在著比較明顯的周期性變化, 大約在每年年積日前120天隨時間變化呈上升趨勢, 年積日120～270天在某個值附近波動, 270～365天隨時間變化呈下降趨勢, 可見Π值隨時間的變化可以用函數來進行表達。

2.2 Π值新模型建立

通過2.1節分析可知, 廣西地區Π值具有比較

明顯的周期性, 可以通過周期函數來進行模型的構建。文獻[11-13]證明了Π值具有年周期, 文獻[12]還證明了Π值具有半年周期。所以, 本文借鑒上述學者研究成果, 采用下式進行模型構建

(6)

式中：doy表示年積日;a0為年平均值;a1、a2為年周期系數;a3、a4為半年周期系數。對廣西4個探空站3年Π值進行擬合分析,得到的擬合系數如表1所示。

表1 廣西4個探空站擬合系數Table 1 Fitting coefficients of 4 radiosonde stations in Guangxi

南寧站的Π值年平均值最大, 梧州站第二, 百色站第三, 桂林站的年平均值最小。4個站點的年周期和半年周期差異較小, 差異主要體現在年平均值上。結合各站點的緯度分析可以發現,Π值年平均值與緯度有關, 緯度越大Π值年平均值越小,Π值與緯度呈負相關關系, 這一結論與文獻[11-13]中的結論一致。文獻[11]還證明了Π值與高程同樣存在著負相關關系， 則利用4個探空站的Π值, 求用戶點處的轉換系數時應進行高程改正

Π′=Π+Δh·λ,

(7)

式中：Π′表示經高程改正后的Π值;Δh表示高差;λ表示Π值隨高程變化的遞減率。

由于Π還與測站緯度有關,故應對高程改正后的Π′值進行緯度改正

Π″=Π′+Δφ·γ,

(8)

式中：Π″表示緯度改正后的Π值;Δφ表示緯度差;γ表示Π值隨緯度變化的遞減率。

綜上所述,利用廣西4個探空站大氣水汽轉換系數計算該區域內用戶點轉換系數的新模型可表示為

Πz=p1Π1″+p2Π2″+p3Π3″+p4Π4″,

(9)

式中:Πz表示用戶點經高程和緯度改正后的總Π值;Π1″、Π2″、Π3″、Π4″表示4個探空站經過高程和緯度改正后的Π值;p1、p2、p3、p4表示4個探空站對應的權重,本文中的權重按緯度變化反比例加權計算。文獻[11]研究了中國低緯度地區Π值隨高程和緯度的變化特征。為方便比較,本文采用其研究成果:γ=-0.000 002/m,λ=-0.000 2/°。

3 模型精度分析

3.1 內符合精度分析

為驗證本文模型的精度, 以探空站數值積分獲得的Π值為參考值, 利用該模型解算出廣西4個探空站3年的Π值與參考值進行比較, 并與廣西高程模型、中國低緯度模型進行精度對比。3種模型在廣西4個探空站點的誤差圖如圖2所示。

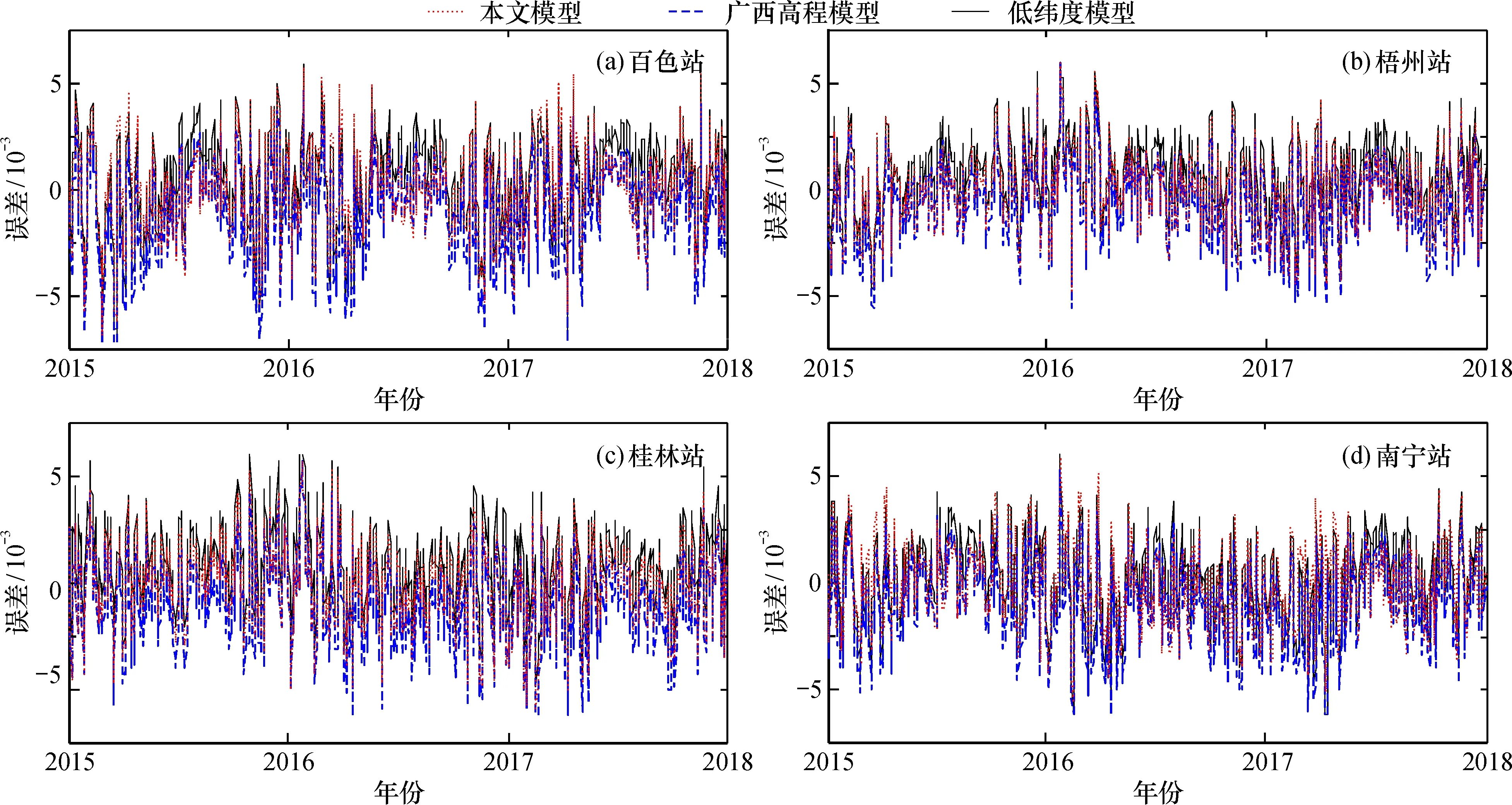
圖2 3種模型的誤差分布Fig.2 Error distribution of 3 models

可見， 3種模型在4個站點3年的誤差都分布在±0.006, 且3種模型的誤差走勢一致。廣西高程模型的誤差偏向于負誤差, 低緯度模型的誤差偏向于正誤差, 本文模型的誤差介于兩個模型誤差中間。為進一步分析3種模型的精度, 現采用平均絕對誤差(MAE)和均方根誤差(RMSE)作為評價指標進行精度評價, 結果見表2。

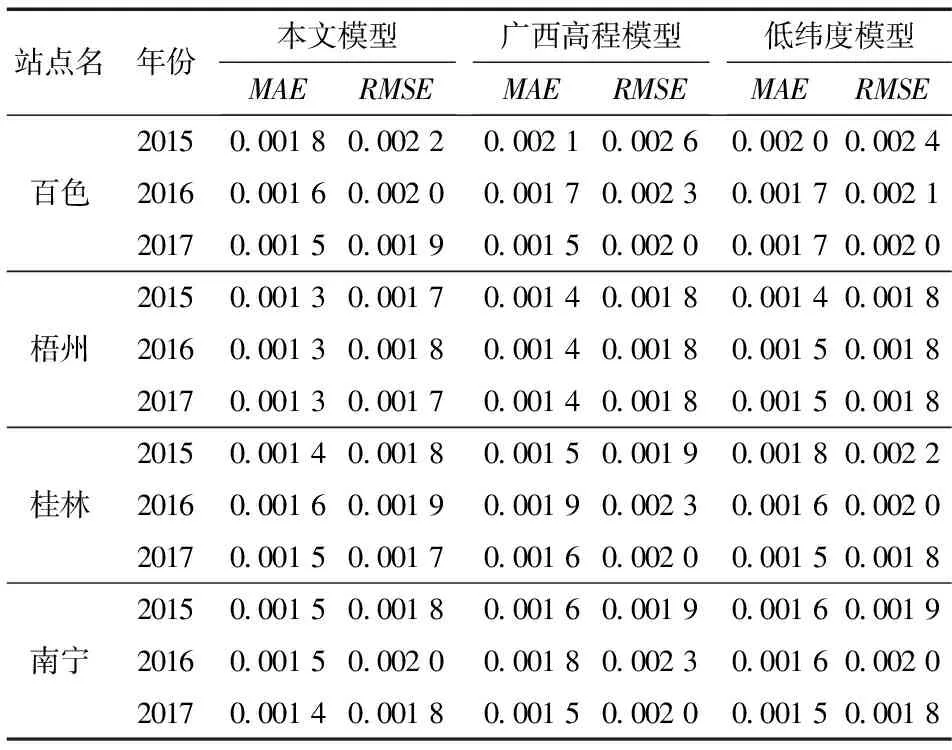
表2 3種模型的精度統計Table 2 Accuracy statistics of 3 models

百色站點: 本文模型的MAE、RMSE值較廣西高程模型和低緯度模型的MAE、RMSE小, 表明在該站點本文模型的精度較其他兩個模型高。

梧州站點: 本文模型的MAE值最小; 2015、2017年, 本文模型的RMSE值最小; 2016年3種模型的RMSE值相同; 綜合3年的MAE、RMSE值可以看出, 本文模型的精度較其他兩個模型高。

桂林站點: 綜合3年的MAE、RMSE值可以看出, 本文模型的精度較其他兩個模型高。

南寧站點: 3種模型的MAE、RMSE值可以看出, 本文模型在該站點精度較其他兩個模型高。

通過對3種模型在4個探空站點3年的誤差分析可以得出結論: 本文模型的內符合精度較廣西高程模型、低緯度模型精度要好, 低緯度模型與廣西高程模型的精度相當。

3.2 外符合精度分析

為驗證該模型外符合精度情況, 利用2018年百色站探空數據積分計算的Π值為參考值, 用該模型預測百色站2018年Π值, 并與廣西高程模型、低緯度模型的預測值進行對比。3種模型預測值的誤差分布情況如圖3所示。

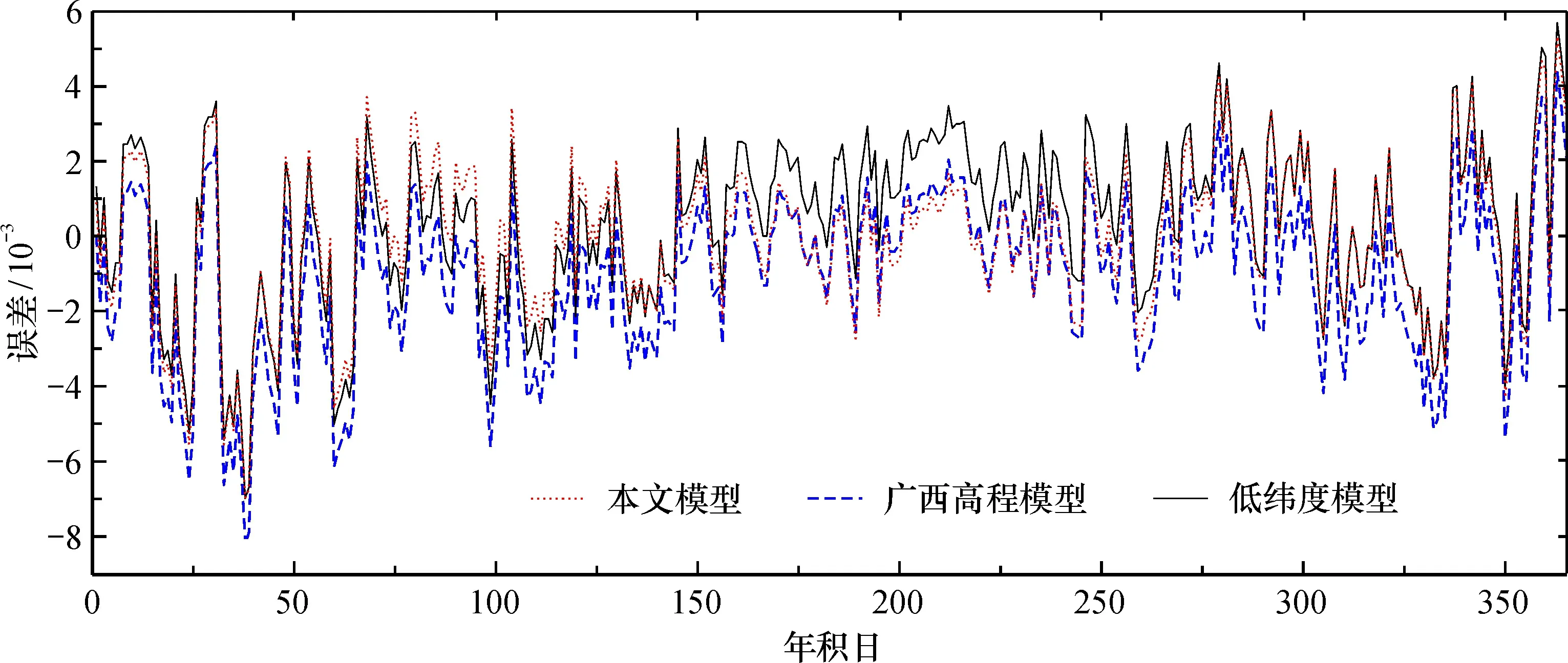
圖3 3種模型的預測誤差Fig.3 Prediction errors of 3 models

可見, 3種模型的誤差較接近, 都在-0.008～0.005。大致在年積日0～70、340～365天左右, 3種模型的誤差波動都較大。同樣, 對3種模型的誤差采用MAE、RMSE值進行統計分析, 結果見表3。

表3 3種模型的預測精度統計Table 3 Prediction accuracy statistics of 3 models

可以看出, 本文模型的MAE、RMSE值都是最小, 廣西高程模型和低緯度模型的MAE值相差很小, 廣西高程模型RMSE值比低緯度模型大。這表明本文模型預測值的精度最高、廣西高程模型的預測精度最低。可見, 本文模型的外符合精度較廣西高程模型、低緯度模型高。

4 模型應用

為了驗證本文模型應用于PWV反演的效果, 本文利用文獻[7]中提供的桂林站PWV數據進行分析。利用了桂林站2015年1月16—23日的氣象數據和CORS數據進行水汽反演實驗, 計算得到探空站的PWV和ZWD值, 將其視為參考值。將文獻[7]中所采用的轉換系數替換成利用本文模型、低緯度模型、廣西高程模型解算得到的轉換系數, 解算出桂林站該時間段對應的PWV, 并將3種模型解算得到的PWV與參考值進行對比, 結果見表4。

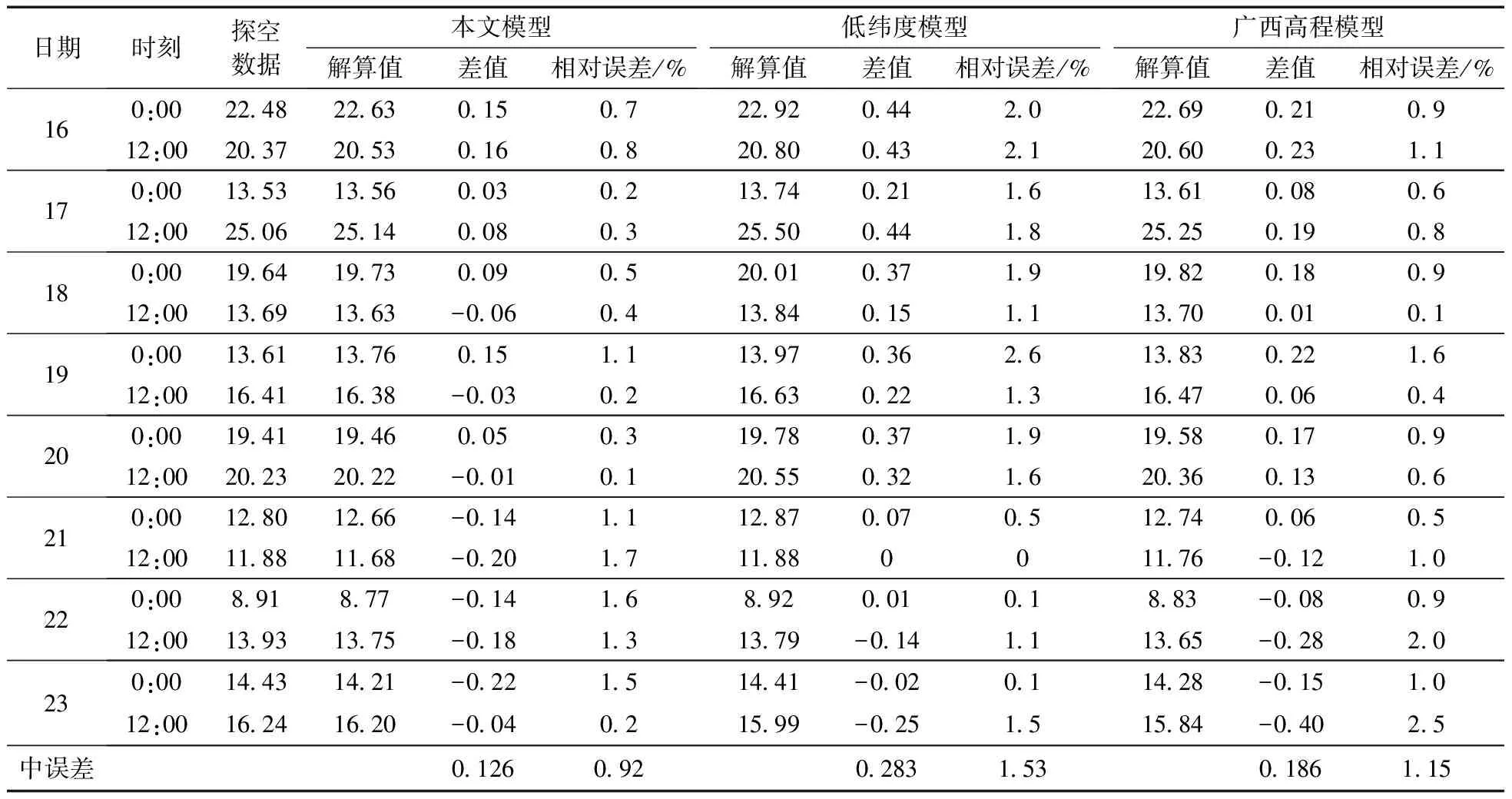
表4 2015年桂林站水汽含量Table 4 PWV of Guilin station in 2015mm

可知, 本文模型、低緯度模型、廣西高程模型與探空站資料積分得到的PWV之差最大為0.22 mm(相對誤差1.5%, 下同)、0.44 mm(1.8%)、0.40 mm(2.5%), 最小為0.01、0、0.01 mm; 中誤差分別為0.126、0.283和0.186 mm, 整體相對誤差分別為0.92%、1.53%和1.15%。 綜合3種模型的中誤差以及相對誤差可以看出, 本文模型精度較低緯度模型、廣西高程模型有一定提升。

5 結束語

本文利用2015—2017年廣西4個探空站資料, 建立了直接反映年周期、半年周期、高程改正和緯度改正的廣西地區大氣水汽轉換系數的計算模型， 并將其與廣西高程模型、低緯度模型進行了內符合精度對比, 利用2018年百色探空站資料進行了外符合精度對比, 同時還利用桂林站2015年1月16—23日的探空數據進行了PWV反演精度的對比分析。 結果表明: 本文模型在內、外符合精度上均優于廣西高程模型和低緯度模型。 PWV反演時, 本文模型的誤差最大值為0.22 mm(相對誤差1.5%), 中誤差為0.126 mm(相對誤差0.92%), 與低緯度模型、廣西高程模型相比精度有一定提高。