數形結合思想在初中數學教學中的滲透分析

韓成軍

【摘 要】本文闡述了數形結合思想運用在初中數學教學中的價值，提出了初中數學教學中數形結合思想的應用策略，以期促進學生數學學習能力提升。

【關鍵詞】數形結合;初中數學;教學質量;邏輯思維

【中圖分類號】G633.6 ?【文獻標識碼】A ?【文章編號】1671-8437（2021）10-0048-02

隨著教育事業(yè)的發(fā)展，教育改革加快推進，初中數學教師突破了傳統(tǒng)教學模式的禁錮和局限，逐漸將數形結合的教學思路引入課堂教學，激發(fā)學生的學習興趣，吸引學生的注意力，培養(yǎng)中學生觀察、分析和解決問題的能力。中學教學中也逐漸提高對數形結合思想運用的重視程度，加強對數形結合教學方法價值的挖掘，確保提升數學課堂教學質量。

1 ? 數形結合思想運用在初中數學教學中的價值

數學學科邏輯性、綜合性較強，相比其他學科，教學難度較大，學生對抽象的知識點難以有效理解和掌握。運用數形結合的教學方法，能使學生更加直觀、形象地感受數學學科的魅力，在激發(fā)學生想象力的同時，培養(yǎng)學生科學探究的能力。通過圖形分解演示，學生的思維會更活躍，解決問題的能力會得到強化，在實際學習中他們能從多個角度對問題進行分析，順利解決數學重難點問題。數學教師一定要通過演示幾何圖形的分解、變換，強化中學生的數形結合思維，使學生的數學應用能力得到提升。

教師在實際教學中應用數形結合的方式，對數學幾何圖形、代數、函數中有關的線和線段進行分解演示，創(chuàng)建一定的空間形態(tài)，能使學生通過尋找函數與數學方程之間的關系，更好地梳理解題思路，得出答案。數形結合思想具有生動性、靈活性特征，是幫助學生探索正確解題思路的關鍵，能活躍學生的思維方式，開發(fā)學生的智力，提高學生解題的正確率，培養(yǎng)學生的創(chuàng)新意識，推動數學高質量課堂的構建。教師應運用數形結合思想，促使學生加強生活實際與數學學科之間的聯(lián)系。在不等式、數軸等難點問題上，教師應為學生提供解題思路，簡化解題路徑，在發(fā)揮數形結合教學優(yōu)勢的同時，增強學生的自信心，提高學生參與數學教學活動的積極性，培養(yǎng)中學生的數學學科素養(yǎng)[1]。初中教師在運用數形結合思想開展教學活動時，應通過案例導圖、數形勾畫的方式進行引導，啟發(fā)學生思考，并將數形結合思想貫穿于學生學習的課前、課中以及課后知識鞏固階段，從而鍛煉學生的思維能力，提升學生的數學學習能力。

2 ? 初中數學教學中數形結合思想的應用策略

2.1 ?創(chuàng)設情境，激發(fā)學生的學習興趣

教師將數形結合思想引入課堂教學，能使學生理解和掌握數形結合學習方法、步驟以及具體的運用情境，并在實際學習中加強與生活實際之間的聯(lián)系。筆者在教學實踐中發(fā)現，教師合理創(chuàng)設情境，會使學生在課堂中更加活躍、興趣更加濃厚，參與課堂學習的主動性提高，有助于獲得顯著的教學效果。數學學科涉及許多公式和定義，學生需要記憶的知識點較多，單一的教學方法難以滿足學生的個性化學習需求。教師可以創(chuàng)設情境，引入數形結合思想，通過數學符號和圖形的運用，幫助學生理解記憶，促進學生融會貫通、舉一反三。如教學人教版“平面直角坐標系”一單元時，在確保學生掌握基礎知識的基礎上，引導學生探索新知，教師在PPT中給出坐標圖形，要求學生準確說出圖中B、C、D以及原點的坐標。學生通過坐標圖形演示，可準確地得出具體的坐標[2]。

再如教學“畫軸對稱圖形”一章節(jié)時，教師可先向學生提問：“如何畫線段，并畫出 AB 關于 l 的對稱線段？”學生根據給出的線段，進行簡單的分析后，會畫出正確的對稱線段A?B?，更加明確圖形是由直線、線段、射線構成，在具體畫出某條直線的對稱軸時，需先找到圖形中的特殊點，然后連接對稱點，這樣就可以畫出這條線段的對稱圖形。

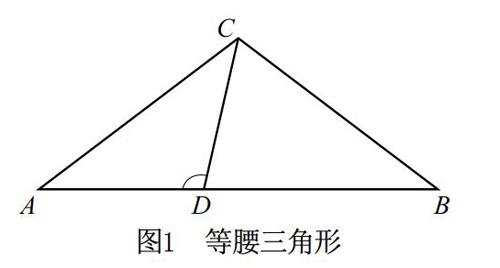
教師要將數形結合思想滲透在教學中，在課前需做好充分的教學準備工作，明確圖形的應用方式，更好地將教學內容講授給學生。基于初中階段數學知識點的復雜性、抽象程度較高，以“形”和“數”的方式開展教學活動，能使學生更容易理解，有助于優(yōu)化學生的解題思路，提高學生的解題效率。如教學“等腰三角形”一章節(jié)中的“求等腰三角形各內角”時，滲透數形結合思想，引導學生在實際解題中根據已知條件，求出三角形各個內角的度數，進而畫出圖形，可降低學生思考的難度，在一定程度上提高學生繪制圖形的準確性。學生根據已知條件進行求證，在數形結合思想下，能精準地計算內角的度數[3]。同時，教師可在此基礎上給出圖形，引導學生判斷“如圖1所示，在?ABC中，AC=BC，∠ADC=∠BDC。”的正誤，讓學生根據所學知識推理出最終的結論。

2.2 ?以形解數

初中數學方程式、不等式教學中，往往需要融入“以形解數”思想，利用圖形的直觀性，將抽象的知識轉化得更生動，降低學生解題的難度，使學生更好地解方程和不等式，增強學習的信心。在解不等式問題的過程中，教師可為學生提供解題思路，通過“形”的運用，解出不等式的公共解集，簡化解題步驟，確保解題的正確性。如在教學人教版“不等式與不等式組”一章節(jié)時，教師可運用數軸的方式，引發(fā)學生思考。

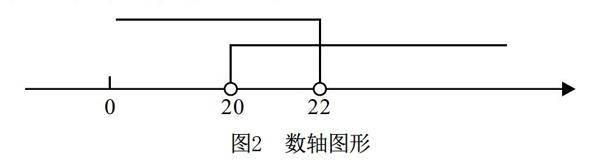
問題1：某學校冬季取暖時間為4個月，計劃比其余月份要多燒5噸煤，則總量超出100噸;反之，計劃比每月少燒5噸煤，總量則為68噸，那么學校實際每月燒煤多少噸？學生會先根據所學的不等式知識進行思考，將未知的每月燒煤數量設為 x ，在多燒5噸煤的情況下，實際每月燒煤 （x+5） 噸，燒煤總量為4（x+5）>100 ;在少燒5噸煤的情況下，實際每月燒煤為 （x?5）噸，燒煤總量為 4（x?5）<68 。教師可引導學生理清題意，根據已知條件，將實際問題轉化為數學模型，將兩個不等式組合起來，表示為 4（x+5）>100 、4（x?5）<68。為降低學生求解的難度，教師可在PPT中給出數軸圖形（如圖2所示），并給足學生討論的時間，讓學生在小組中自主探究如何確定不等式的解集。學生最終會得出 x 的值必須要同時滿足大于20以及小于22，進而確定 20

2.3 ?數形結合

學習函數知識內容時，學生對抽象的函數關系難以理解，思路容易混亂。對此，教師可將數形結合思想滲透在教學中，使學生能梳理自己的解題思路，加強對函數知識點的記憶。函數與平面圖形通常是對應的，如在教學 y=kx+b（k≠0）函數式時，由于 k、b 的值與平面圖形有一定的對應關系，教師可采取圖形解析教學方式，使學生更容易理解，更好區(qū)分圖形與函數式之間的關系，降低解題的難度，提高函數問題的解題效率，推動數學課堂高質量開展。教師在實際教學中，針對復雜的函數問題、方程問題、幾何問題等，需要充分利用數形結合思想。同時，教師要根據學生的實際，尊重學生的個性化特征，培養(yǎng)學生的數形結合思維，提升學生的邏輯思維能力，使學生積極在數學學習中掌握學習技巧、解題技巧，更好地運用所學知識加強對數學重難點知識的探究，通過數形結合方法的運用，進一步提升觀察、分析、解決實際問題的能力。

綜上所述，數形結合是初中教育教學中新型的教學手段，數形結合思想的運用能夠優(yōu)化數學學科教學環(huán)節(jié)，拓展學生的視野，幫助教師加強對學生的引導，促使學生快速找出解題思路，增強中學生分析習題的能力。隨著數形結合思想在實際教學中的不斷滲透，教師會發(fā)現，學生的思維更加活躍，他們的邏輯能力、思考能力顯著提升，解題方案更多元化。這證明了數形結合思想在數學教學中應用的可行性，因此，教師要運用數形結合思想進一步創(chuàng)新和完善教學方法，促進學生綜合能力的提升。

【參考文獻】

[1]李峰云.數形結合思想在初中數學教學中的滲透分析[J].教育革新，2020（8）.

[2]白輝.數形結合思想在初中數學教學中的滲透[J].科學咨詢（教育科研），2020（4）.

[3]凌春花.在初中數學教學中滲透數形結合思想[J].中國農村教育，2019（27）.