一種姿態測量系統的FPGA和DSP設計與實現

呂金銳

摘? 要： 為了實現對某彈載系統的姿態測量，提出一種基于FPGA+DSP的姿態測量系統的設計。系統采用FPGA作為邏輯控制核心，完成對MEMS傳感器輸出的陀螺加表數據的采集，并通過EMIF接口完成與DSP的數據通信。DSP完成對姿態信息的解算，并由FPGA通過RS422接口將更新后的姿態信息上傳至上位機。系統選用地理坐標系作為導航坐標系，利用四元數法及Kalman信息融合算法對采集到的姿態信息進行解算。測試結果表明，該系統輸出的姿態信息精度較好，總體角誤差在0.5°以內。

關鍵詞： MEMS傳感器; 姿態測量; FPGA+DSP; 四元數; Kalman信息融合; 姿態解算

中圖分類號：TN702? ? ? ? ? 文獻標識碼：A? ? ? ? ? ? 文章編號：1006-8228（2021）05-29-04

Design and implementation of FPGA and DSP for attitude measurement system

LV Jinrui

（Department of Information Engineering， Taiyuan City Vocational college， Taiyuan， Shanxi 044000， China）

Abstract： A kind of attitude measurement system based on FPGA and DSP is proposed to realize the attitude measurement of a projectile-borne system. The system uses FPGA as the core of logic control to collect the gyro table data output by MEMS sensor and to communicate data with DSP through EMIF interface; The DSP completes the resolution of the attitude information， while the FPGA uploads the updated attitude information to the upper computer through the RS422 interface. Geographic coordinate system is chosen as navigation coordinate system， and the attitude information collected is solved by Quaternion method and Kalman information fusion algorithm. The test results show that the accuracy of attitude information output by the system is good， and the overall angle error is within 0.5.

Key words： MEMS sensor; attitude measurement; FPGA and DSP; Quaternion; Kalman information fusion; attitude resolution

0 引言

姿態解算作為姿態測量系統中的核心部分，正朝著高精度和高速度的方向發展[1]。為實現更加準確的對彈載系統的姿態測量，不僅對數據的采集及處理算法提出更高的要求，同時對于處理器的選擇也越來越重視。在測量系統中，確定姿態主要運用的是陀螺，但由于陀螺儀長期工作存在精度測量漂移從而無法保證系統精度，對姿態的確定會產生很大的偏差[2]。針對以上問題，系統采用ADIS16488傳感器為核心，結合FPGA的并行處理方式以及DSP強大的數據處理能力，構建了一個姿態測量系統。

1 系統總體設計

系統采用美國AD公司產品ADIS16488 MEMS慣性傳感器作為核心，其內部集成了三軸微陀螺儀，三軸微加速度計，三軸微磁強計以及壓力傳感器[3]。當MEMS慣性傳感器處于工作模式時，能夠同時采集三個軸向上的加速度、角速度及磁強度。

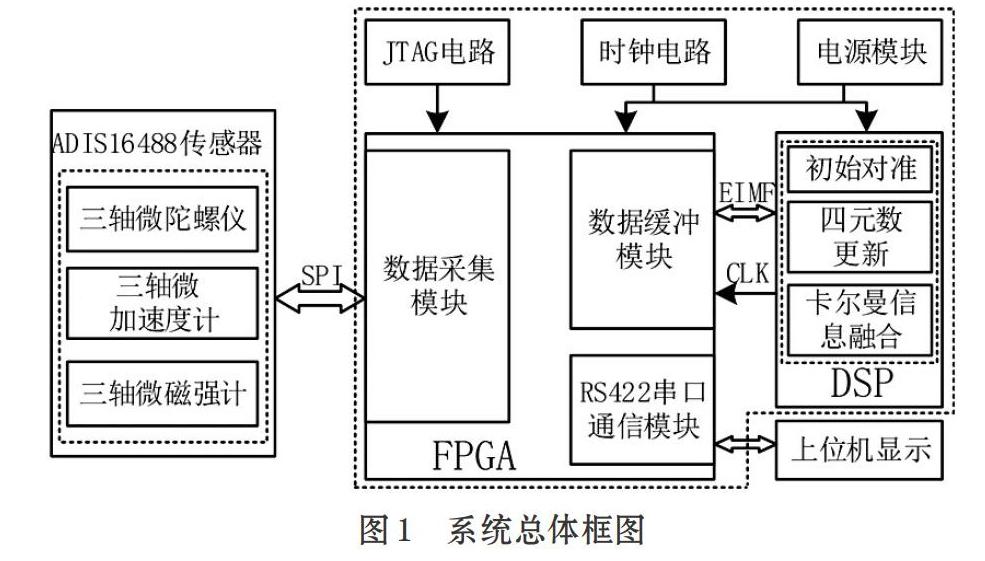
系統總體結構圖如圖1所示。系統工作原理：FPGA作為主控芯片，首先通過SPI接口對傳感器進行初始化配置，然后根據上位機指令采集傳感器輸出的陀螺加表等數據至數據緩沖模塊，通過EMIF接口將數據傳輸至DSP進行數據處理，最后將解算好的姿態信息通過RS422發送模塊上傳至上位機進行顯示。

2 硬件電路設計

2.1 傳感器數據采集模塊

慣性測量單元正常工作時，需加載3.3V電壓至10、11、12引腳[4]。上電后，系統首先通過FPGA完成對傳感器的初始化配置，然后SPI接口來讀取更新后的傳感器數據。傳感器內部寄存器采用分頁結構，每一頁都對應其相應的功能[5]。FPGA對MEMS傳感器進行讀寫時需要連續兩個8bit地址進行操作，其中低地址在前，高地址在后。高8bit地址表示傳感器內部相應寄存器的地址，低8bit地址表示寫入該寄存器的數據內容。如圖2所示，對傳感器進行讀操作時需要一個16bit的寄存器地址，且相應寄存器地址上的數據輸出將在下一個寄存器地址輸入時才會輸出。

2.2 FPGA與DSP通信接口設計

FPGA與DSP通過EMIF接口來實現通信，如圖3所示，EMA_DATA[15：0]為數據總線，EMA_WE為FIFO讀使能信號，GPIO4_15為啟動數據發送信號，EMA_CS為EMIF使能信號。為匹配數據傳輸速率，采用雙端口RAM來對讀取的DSP數據進行緩存，在雙端口RAM模塊和DSP模塊之間串聯33Ω電阻來減少信號失真[6]。雙口RAM發送模塊不僅實現了數據的讀寫獨立，也滿足了數據在發送時間上的要求。

3 姿態解算算法

3.1 初始姿態對準

在求解載體姿態前對系統進行初始對準，對于提高姿態信息精度有很大的影響。首先利用載體在地理坐標系的投影[00gT]和在載體坐標系的投影[fxbfybfzbT]，得出載體橫滾角和俯仰角，然后利用求得的初始橫滾角和俯仰角計算初始航向角[7]。算法推導過程如下：

[fxbfybfzb=Cnb00g]=[cosγcosγsinθ-sinγcosθ0cosθsinθsinγ-sinγsinθcosγcosθ][ 00g]

求解得初始橫滾角和俯仰角：

[θ=sin-1][fyb/g]

[γ=tan-1-fxb/fzb]

結合磁強計由載體坐標系映射到磁場x、y方向上的值，求解得：

[Hx=mxcosθ+mysinγsinθ+mzcosθsinγ]

[Hy=mycosγ-mzsinγ]

然后求得初始航向角：

[ψ=arctanHy/Hx]

3.2 四元數法

根據歐拉定理可知，載體坐標系b相對于地理坐標系n的方位相當于b系繞定軸轉動3次方位角，四元數包含了轉動的信息[8]。[un]為旋轉軸和旋轉方向，θ為轉過的角度。

[Q=cosθ2+unsinθ2]

利用哥式等式推導得出四元數的微分方程為：

[Q=12Q?ωbnb]

矩陣形式為：

[T0T1T2T3=0-ωx-ωy-ωzωx0ωz-ωyωyωz-ωzωy0ωx-ωx0]

然后利用四階龍格庫塔法求得四元數更新表達式：

[k1=T2ωbt?qt]

[k2=T2ωbt+T2?qt+k12]

[k3=T2ωbt+T2?qt+k22]

[k4=T2ωbt+T2?qt+k3]

[qt+T=q（t）+][T6][k1+2k2+2k3+k4]

四元數可確定出載體坐標系到地理坐標系的坐標轉換公式：

[Cnb=q20+q21-q22-q232q1q2-q0q32q1q3+q0q22q1q2+q0q3q20-q21+q22-q232q2q3-q0q12q1q3-q0q22q2q3+q0q1q20-q21-q22+q23]

3.3 卡爾曼濾波

卡爾曼濾波的主要作用在于最大限度的減小噪聲目標信號的影響，利用不同時刻的系統狀態信息，對信息預測和估計，最終得到一個較為精確的數值。它相當于一個動態遞歸的過程：

[Xk=AkXk-1+Bkuk-1+wk-1]

[Zk=HkXk+vk]

其中，Xk為k時刻的系統狀態，Zk表示k時刻的觀測變量。uk為K時刻對系統的控制量。vk，wk分別表示狀態方程的觀測噪聲和過程噪聲。Hk是觀測噪聲誤差狀態增益矩陣，Ak和Bk是系統參數[9]。

卡爾曼濾波的時間更新公式為：

[X-k=AXk-1+Buk-1]

[P-k=APk-1AT+Q]

由k-1時刻的最優值[Xk-1]去預測k時刻系統的狀態值[X-k]。然后由上一次的誤差協方差[Pk-1]和過程噪聲Q預測新的誤差[10]。

卡爾曼濾波的狀態更新公式為：

[Kk=P-kHTHP-kHT+R-1]

[Xk]=[X-k+KkZk-HX-k]

[Pk=I-KkHP-k]

計算卡爾曼增益Kk，并進行校正更新，得到的[Xk]即為k時刻的最優估計值。為下一步估計k+1時刻的最優估計值的迭代進行更新操作，即更新Pk。

3.4 小波閾值降噪

由于ADIS16488內部的MEMS陀螺儀的抗干擾能力較弱，產生的噪聲相對于其他兩個傳感器而言更大。因此系統結合陀螺儀輸出信號不具備線性的特點，選用小波閾值降噪算法來對進行降噪處理。小波閥值消噪原理如圖4所示。

系統進行了對靜置的傳感器進行了降噪實驗，系統上電后對陀螺儀y軸數據進行采集，采樣頻率為200Hz，采樣時間為100s，得到陀螺儀的實時數據如圖5所示。

由圖5可以看出，當陀螺儀靜置時，其y軸輸出的角速率誤差值較大，范圍在[-0.04°，-0.04°]。對該陀螺儀采用小波閾值降噪處理后，得到如圖6所示的誤差波形圖。由圖6可以看出，陀螺儀靜置時y軸輸出的波形有了明顯的改善，角速率誤差約束到了[-0.02°，-0.02°]。

4 系統測試

4.1 傳感器數據采集模塊仿真

傳感器輸出的數據對于整個測量系統來說有著十分重要的作用，它關乎著數據的正確性和完整性。FPGA負責接收傳感器輸出的數據并將其緩存至內部RAM中，同時也負責讀出DSP解算后緩存至RAM中的數據，并將其上傳至上位機。為了驗證FPGA與DSP之間通信的正確性，將在FPGA RAM中寫入數據0-256，DSP通過EMIF接口讀取RAM中的數據，在開發環境ISE下顯示DSP讀取的數據以及其他信號的一些變化，它讀取的數據地址空間是從0xc0000000開始。如圖7所示，DSP與FPGA之間通信正確。

4.2 誤差分析

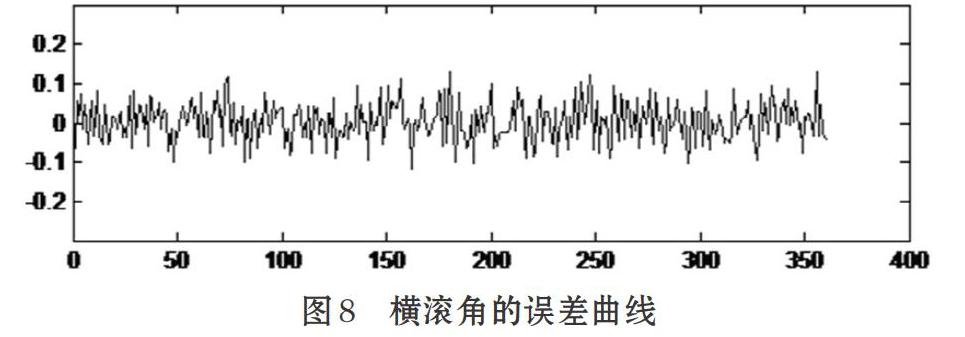
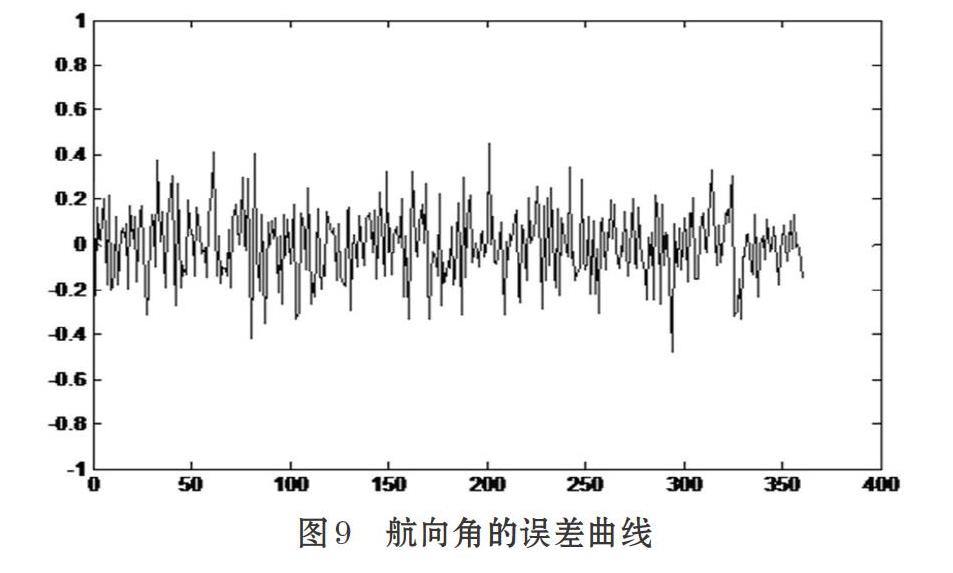
為了對系統性能進行測試與驗證，采用AHRS（商業級姿態參考系統）作為參考。驗證過程中，將該參考系統與電路板固定，并置于三軸無磁轉臺中。未上電之前調整軸向，使得系統坐標系和轉臺的軸向一致。以z軸為定軸進行5°/s的轉動，采集時間為360s，數據采集完成后通過串口上傳至上位機。上位機對接收到的數據進行分析計算，采用Matlab對接收到的數據進行曲線顯示，如圖8、圖9、圖10所示。

由于系統在進行測試時選用z軸為定軸進行轉動，從得到的誤差曲線圖中可以看出，橫滾角和俯仰角的誤差較小，均在0.4°以內，姿態解算精度較好。即驗證了系統在轉動過程中，x軸和y軸方向的姿態沒有發散。

將系統姿態解算的結果與AHRS測量的數據進行比較，得出其誤差的標準差，如表1所示。驗證系統解算的結果較好，誤差值均在0.5°以內。

4.3 上位機數據顯示

系統通過RS422接口將解算好的姿態信息發送至上位機進行顯示，如圖11所示。圖11為傳感器繞z軸轉動時，三個軸向角度的變化曲線圖。如圖12所示，可以直觀的看到傳感器的全姿態信息。

5 結束語

系統采用FPGA+DSP雙處理器的方案來實現對某彈載控制器的姿態解算，通過系統測試，驗證該姿態測量系統的輸出精度較好，均在0.5°以內，能夠滿足技術要求。這為后續測量系統的進一步優化提供了可靠的實驗數據。

參考文獻（References）：

[1] 沈懷營，吳伯衣.基于DSP/FPGA的高速旋轉體姿態角及轉速的解算系統設計[J].山西電子技術，2012.3（1）：41-43

[2] 李炳炳.基于MEMS慣性傳感器的人體姿態檢測系統的研究[D].南京理工大學，2017.

[3] 楊陽.基于ADIS16488 MEMS慣性組合姿態測量設計與研究[D].中北大學，2015.

[4] 廖文平.基于MEMS傳感器的姿態解算的FPGA實現[D].長沙理工大學，2015.

[5] 李越.四旋翼無人機姿態解算及控制研究[D].昆明理工大學，2017.

[6] 張銳.基于FPGA的小型捷聯式慣性導航系統研究[D].中國民航大學，2014.

[7] 楊兆靜.基于FPGA的載體姿態角解算算法的研究與設計[D].燕山大學，2013.

[8] 楊龍，李范鳴.DSP EMIF與FPGA雙口RAM高速通信實現[J].現代電子技術，2016.37（13）：10-13

[9] 文雨辰.基于FPGA+DSP架構的GPS接收機設計和實現[D].電子科技大學，2010.

[10] 張榮輝，賈宏光.基于四元數法的捷聯式慣性導航系統的姿態解算[J].光學精密工程，2008.16（10）：1963-1970