A REMARK ON GENERAL COMPLEX(α,β)METRICS?

(夏紅川)

School of Mathematics and Statistics,Xinyang Normal University,Xinyang 464000,China

E-mail:xhc@xynu.edu.cn

Chunping ZHONG(鐘春平)

School of Mathematical Sciences,Xiamen University,Xiamen 361005,China

E-mail:zcp@xmu.edu.cn

Abstract In this paper,we give a characterization for the general complex(α,β)metrics to be strongly convex.As an application,we show that the well-known complex Randers metrics are strongly convex complex Finsler metrics,whereas the complex Kropina metrics are only strongly pseudoconvex.

Key words Strongly convex;strongly pseudoconvex;general complex(α,β)metrics

1 Introduction

In Hermitian geometry,a Hermitian metric on a complex manifold is necessarily a Riemannian metric which is compatible with the complex structure of the ambient complex manifold.In complex Finsler geometry,complex Finsler metrics are not tightly related to real Finsler metrics;a complex Finsler metric is not necessarily a real Finsler metric,and vice versa.Roughly speaking,a complex Finsler metric on a complex manifold is called strongly convex if it is also a real Finsler metric[1].It is well known that in bounded strictly convex domains with smooth boundary in Cn,the Kobayashi metrics and Carathéodory metrics coincide,and are smooth,strongly convex,weakly K?hler Finsler metrics with a constant holomorphic curvature of?4[2,9,10,12];unfortunately,even in this case,we do not have explicit formulae for the Kobayashi and Carathéodory metrics.So far as the authors’knowledge goes,over the past decade,many results on complex Finsler geometry have been obtained under the assumption that the involved abstract complex Finsler metrics are strongly convex,although there is a lack of concrete examples of strongly convex complex Finsler metrics;for more details,we refer to[7,8,18,20,21,23]and the references therein.It is worth mentioning that strongly convex complex Finsler metrics actually build a bridge between real and complex Finsler geometry,and our recent results on the relationship between flag curvature and holomorphic curvature associated to a strongly convex weakly K?hler Finsler metric confirm this fact[18].Until recently,in order to construct special complex Finsler metrics,we systematically investigated the unitary invariant complex Finsler metrics[13,15,16,22],general complex(α,β)metrics[17],and modified complex Finlser metrics arising from unitary invariant metrics[19]and product complex Finsler manifolds[14],and showed that there exist lots of weakly complex Berwald metrics,complex Berwlad metrics and complex Finsler metrics with vanishing holomorphic curvature;as a byproduct,we showed that there are bundles of strongly convex complex Finsler metrics.In[13],Wang,Xia and Zhong obtained a necessary and sufficient condition for U(n)-invariant complex Finsler metrics to be strongly convex.However,the sufficient condition for a general complex(α,β)metric to be strongly convex given in[17]is too strong(see(3.2));we could not even conclude whether a complex Randers metric,maybe the simplest complex(α,β)metric,is strongly convex or not.In view of the above,we need further investigation of the characterization of strong convexity of complex(α,β)metrics.

The remainder of this paper is organized as follows:in Section 2,we introduce some necessary definitions and notions.In Section 3,we deduce a necessary and sufficient condition for a general complex(α,β)metric to be a strongly convex complex Finsler metric.As an application,we show that the complex Randers metrics are strongly convex complex Finsler metrics,and the complex Kropina metrics are only strongly pseudoconvex complex Finsler metrics which are not strongly convex.

2 Preliminaries

Let us recall some necessary notations and definitions,which can be found in[1].Let M be a complex n-dimensional manifold with the canonical complex structure J.Denote by TRM the real tangent bundle,and TCM the complexified tangent bundle of M.Then J acts in a complex linear way on TCM so that TCM=T1,0M⊕T0,1M,where T1,0M is the holomorphic tangent bundle of M.We also denote by J the complex structure on T1,0M,if it causes no confusion.Let{z1,···,zn}be a set of local complex coordinates on M,with zμ=,so that{x1,···,xn,x1+n,···,x2n}are local real coordinates on M.Denote by{z1,···,zn,v1,···,vn}the induced complex coordinates on T1,0M,with vμ=uμ+so that{x1,···,x2n,u1,···,u2n}are local real coordinates on TRM.

In what follows,we shall denote by?M the complement of the zero section in TRM or T1,0M,depending on the real or complex situation.Unless otherwise stated,we always assume that lowercase Greek indices such asμ,ν etc.run from 1 to n,whereas lowercase Roman indices such as i,j,etc.run from 1 to 2n.The Einstein summation convention is assumed throughout the paper.

The bundles T1,0M and TRM are isomorphic.We choose the explicit isomorphismo:T1,0MRM with its inverseo:TRM1,0M,which are respectively given by

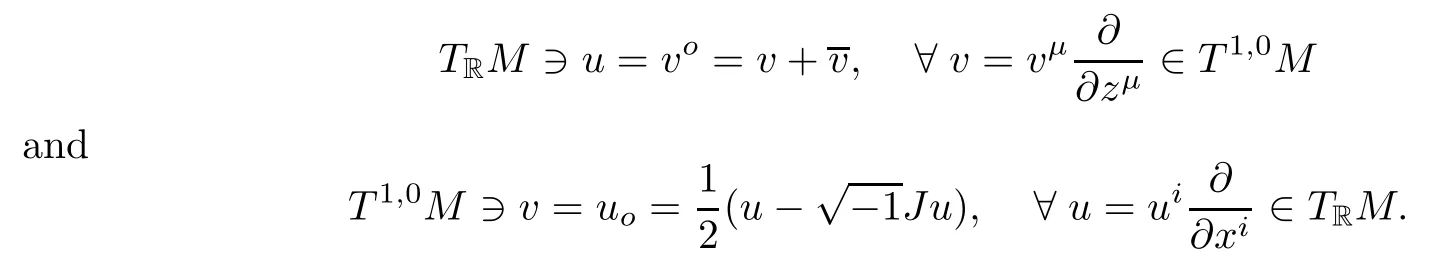
Definition 2.1([1])A real Finsler metric on a manifold M is a function F:TRM→R+satisfying the following properties:

(a)G=F2is smooth on;

(c)F(p,λu)=|λ|F(p,u)for all(p,u)∈TRM and λ∈R;

(d)for any p∈M the indicatrix IF(p)={u∈TpM|F(p,u)<1}is strongly convex.

Note that condition(d)is equivalent to the matrix

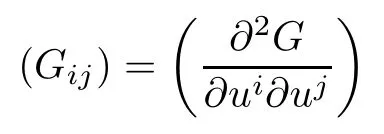
Definition 2.2([1]) A complex Finsler metric F on a complex manifold M is a continuous function F:T1,0M→R+satisfying that

(i)G=F2is smooth on;

(ii)F(p,v)>0 for all(p,v)∈;

(iii)F(p,ζv)=|ζ|F(p,v)for all(p,v)∈T1,0M and ζ∈C.

Definition 2.3([1]) A complex Finsler metric F is called strongly pseudoconvex if the Levi matrix(or complex Hessian matrix)

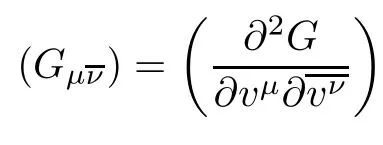
Let F:T1,0M→R+be a complex Finsler metric on a complex manifold M.Using the complex structure J on M and the bundle mapo:TRM1,0M,we can define a real function Fo:TRM→R+by setting

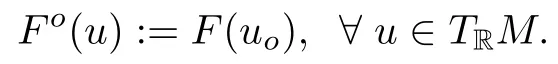
Definition 2.4([1]) A complex Finsler metric F is called strongly convex if the associated function Fois a real Finsler metric.

For a strongly convex complex Finsler metric F,we use the same symbol F to denote the associated real Finsler metric Fowith the understanding that F(u)is defined by F(uo)for u∈TRM.

In what follows,for functions defined onwe shall use lowercase indices to denote the derivatives with respect to the v-coordinate or u-coordinate depending on the complex or real situation;for example:

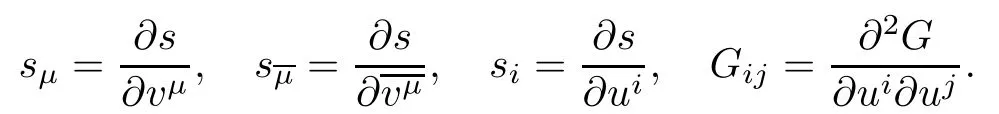
In[17],we introduced a class of smooth complex Finsler metrics,called general complex(α,β)metrics,by using a Hermitian metricand a(1,0)-type differential form β=bμ(z)dzμon a complex manifold M,which are of the form

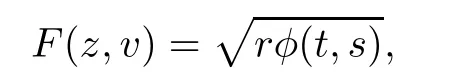
where φ(t,s):[0,+∞)×[0,+∞)→(0,+∞)is a smooth function of t and s,and r,t,s are defined by

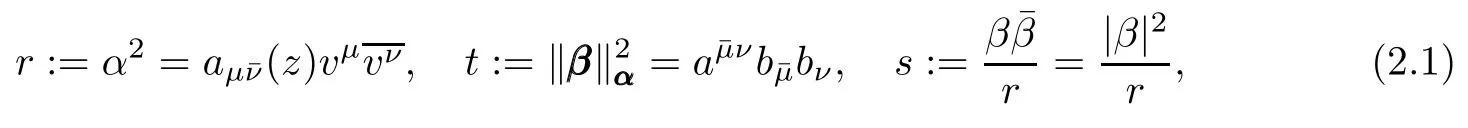
It is noted that the general complex(α,β)metrics include complex(α,β)metrics and unitary invariant complex Finsler metrics as special cases.

3 The Characterization for General Complex(α,β)Metrics to Be Strongly Convex

Before giving the characterization of the strong convexity of general complex(α,β)metrics,we list some basic results which can be found in[17].

Proposition 3.1([17])A complex Finsler metricdefined on M with r,t,s given by(2.1)is strongly pseudoconvex if and only if φ satisfies

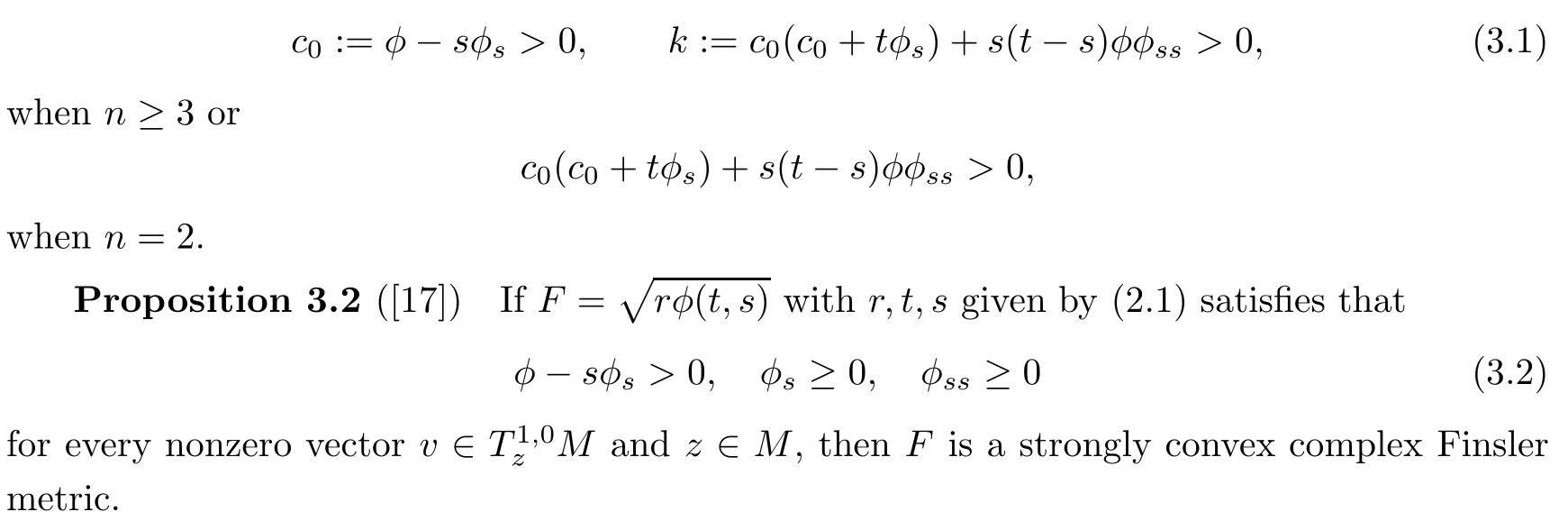
Proposition 3.3([17])For the inverse tensorof the fundamental tensorassociated to the Hermitian metric α2,the following equalities hold:

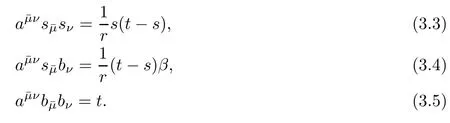
To prove our main result,we need the following lemma:

Lemma 3.4Let U be an n×n Hermitian matrix with decompositionHere P and Q are n×n real matrices,and ξ,η and ζ need to be real or complex n-dimensional row vectors.

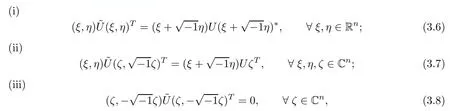
where the upper indices “T” and “?” denote a transpose and Hermitian transpose of a vector or matrix,respectively.

ProofSince U=is a Hermitian matrix,it follows that

Then,calculating both sides in(3.6)–(3.8)and using(3.9)gives the assertions.□

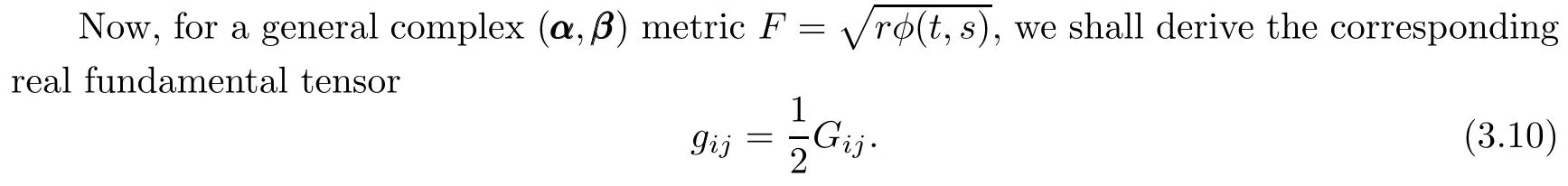
A simple calculation gives that

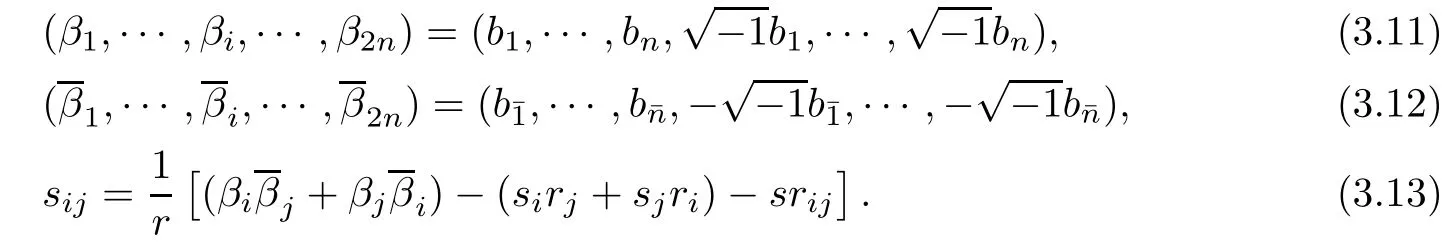
Differentiating G=rφ(t,s)with respect to uiand ujsuccessively,we get

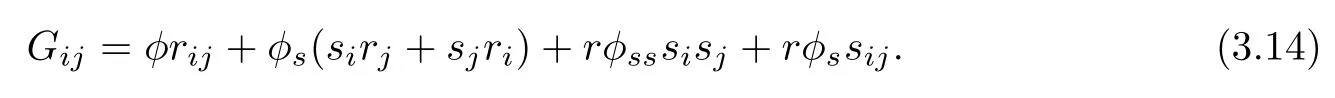
Plugging(3.13)and(3.14)into(3.10)yields

Then

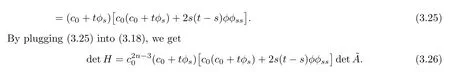
Theorem 3.5Let F=be a general complex(α,β)metric on a complex manifold M with r,t,s given by(2.1).Then F is strongly convex if and only if φ satisfies

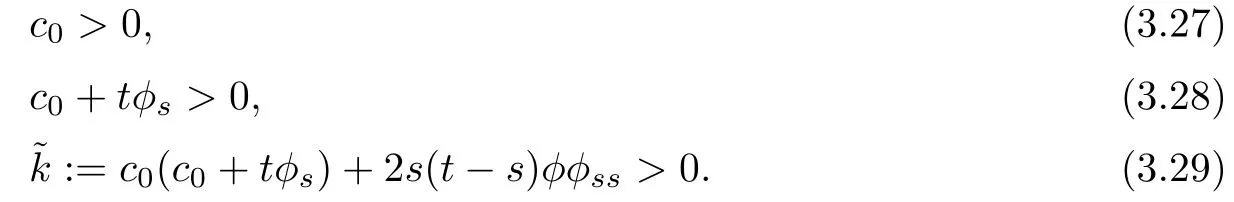
ProofBy definition,F is strongly convex if and only if the corresponding real fundamental tenor matrix H is positive definite,that is,

The sufficiency comes from an argument similar to that of the proof of[22,Proposition 2.6].Hence we only need to prove the necessity.Suppose that F is strongly convex;that is,(3.30)holds.Without loss of generality,we assume that n≥2,since when n=1,the metric F reduces to a Hermitian metric.In this case,the rank of the 2n×2n real matrix KXK?satisfies

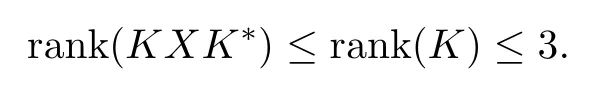
Then we can choose a nonzero row vector ξ∈R2nsuch that ξKXK?ξ?=0.It follows from(3.17)and(3.30)that

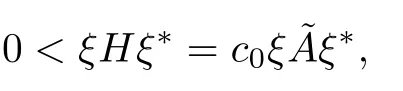
which,together with the fact that>0,implies that

On the other hand,by(3.30)and(3.26),we obtain

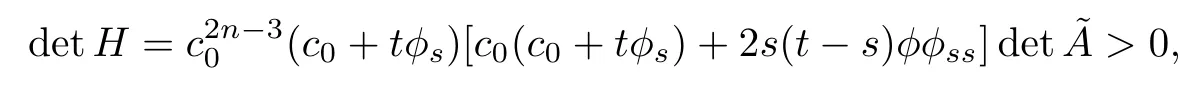
which,together with(3.31),yields

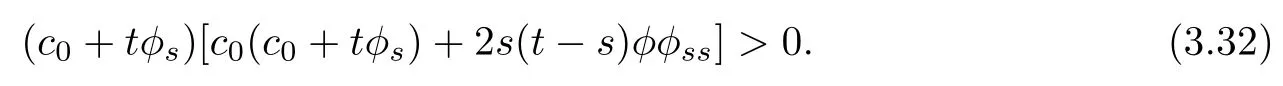
By(3.32),it is necessary that both c0+tφsand c0(c0+tφs)+2s(t?s)φφssare identically greater than 0 or identically less than 0.Noting that when s=t we have c0+tφs=φ>0 and c0(c0+tφs)+2s(t?s)φφss=c0φ>0,it follows that for any s and t,

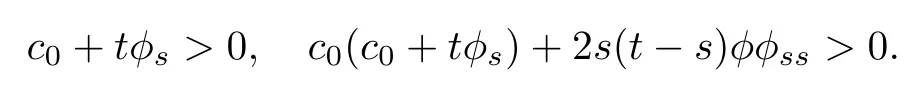
This completes the proof.□

Remark 3.6It is well-known that for domains in Cn,the strong convexity(or Euclidean convexity)is stronger than strong pseudoconvexity.Thus the strong convexity of the indictrix associated to a complex Finsler metric implies the strong pseudoconvexity,that is,a strongly convex complex Finsler metric is necessarily strongly pseudoconvex.A direct comparison of Proposition 3.1 and Theorem 3.5 shows that(3.27)–(3.29)imply(3.1),which con firms the above fact.

Remark 3.7Theorem 3.5 is a generalization of[13,Theorem 4.4],and it is also applicable for general complex(α,β)metrics which have singularities,since we only need to consider matters on the subset of a slit holomorphic tangent bundle where they are smooth.

In[19],we studied a class of modified complex Finsler metrics arising from unitary invariant complex Finsler metrics on a domain D?Cn,which are of the form

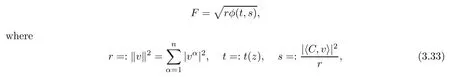
and t=:t(z)is a nonconstant smooth real-valued function of z=(z1,···,zn)∈D,C=(C1,···,Cn)is a nonzero constant vector,φ(t,s)is a smooth positive function of t and s.By a similar method as to that in Theorem 3.5,we have the following proposition:

Proposition 3.8Letbe a complex Finsler metric on a domain D?Cnwith r,t,s given by(3.33).Then F is strongly convex if and only if φ satisfies

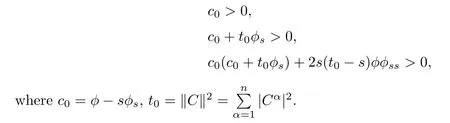
Noting that the complex Randers metrics and complex Kropina metrics are computable,these two classes of metrics attract lots of interest,although they have singularities.For more details we refer to[3,4,6,11]and the references therein.In what follows,as applications of Theorem 3.5,we shall investigate the strong convexity of complex Randers metrics and complex Kropina metrics.

Theorem 3.9Any complex Randers metric F=α+|β|on a complex manifold is a strongly convex complex Finsler metric.

ProofWe only need to verify that F=α+|β|satisfies(3.27)–(3.29).The corresponding function φ associated to F is

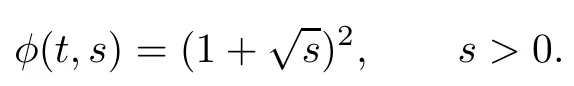
A direct calculation gives that

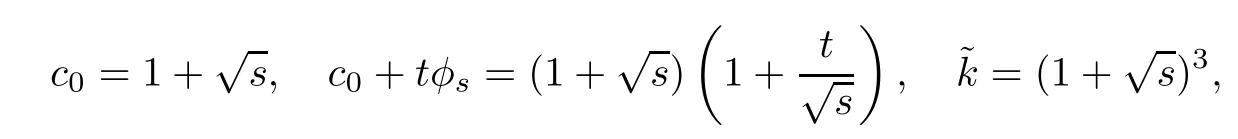
which obviously satisfies(3.27)–(3.29).This completes the proof.□

Remark 3.10In[5],Aldea and Kopacz stated that for complex Randers metric F=α+|β|,a strongly pseudoconvex property is determined by t∈(0,1].Actually,by Theorem 3.9,the condition t∈(0,1]is needless.

Theorem 3.11Any complex Kropina metricon a complex manifold is a strongly pseudoconvex complex Finsler metric,but F is not strongly convex.

ProofThe corresponding function φ associated to the complex Kropina metricis

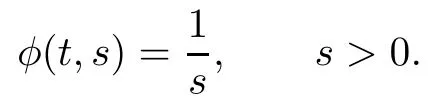
A direct calculation gives that

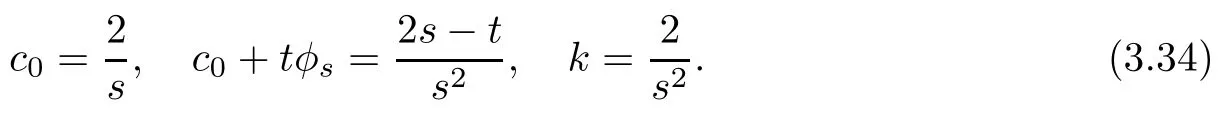
By(3.34),c0>0 and k>0 for s>0,hence F is a strongly pseudoconvex complex Finsler metric.However,c0+tφs<0 when s<,so it follows that F is not strongly convex.This completes the proof.□