STABILITY ANALYSIS OF CAUSAL INTEGRAL EVOLUTION IMPULSIVE SYSTEMS ON TIME SCALES?

(徐家發)

School of Mathematical Sciences,Chongqing Normal University,Chongqing 401331,China

E-mail:xujiafa292@sina.com

Bakhtawar PERVAIZ Akbar ZADA

Department of Mathematics,University of Peshawar,Peshawar 25000,Pakistan

E-mail:Bakhtawar@uop.edu.pk;zadababo@yahoo.com

Syed Omar SHAH

Department of Physical and Numerical Sciences,Qurtuba University of Science and Information Technology Peshawar,Dera Ismail Khan,Pakistan

E-mail:omarshah89@yahoo.com

Abstract In this article,we present the existence,uniqueness,Ulam-Hyers stability and Ulam-Hyers-Rassias stability of semilinear nonautonomous integral causal evolution impulsive integro-delay dynamic systems on time scales,with the help of a fixed point approach.We use Gr?nwall’s inequality on time scales,an abstract Gr?wall’s lemma and a Picard operator as basic tools to develop our main results.To overcome some difficulties,we make a variety of assumptions.At the end an example is given to demonstrate the validity of our main theoretical results.

Key words Time scale;Ulam-Hyers stability;impulses;semilinear nonautonomous system;Gr?nwall’s inequality;dynamic system

1 Introduction

The study of functional equations with causal operators has seen rapid development in the last several years;some recent results are assembled in the monograph[8].The term of causal operator is adopted from engineering literature and the theory of these operatorsunifies ordinary differential equations,integro-differential equations with finite or infinite delay-Volterra integral equations,neutral functional equations etc.Many articles have addressed various aspects of the notion of causal operators.In[17],a general and new definition of Volterra operators in the sense of Toneli was given.Control problems having casual operators were studied in[2,9,16,38].Some properties of solutions of the differential equations with causal operators can be seen in[13–15,17,18].

The famous stability of functional equations was introduced by Ulam in 1940 at Wisconsin University[47,48].The problem involved discussing the relationship between an approximate solution of a homomorphism from a group G1to a metric group G2.In the following year,Hyers partially gave the solution to Ulam’s problem by taking G1and G2as a Banach spaces(BS’s)[25].Since then,this notion has been called Ulam-Hyers(UH)stability.The Hyers result was then generalized by Rassias[35],which gave rise to the notion of Ulam-Hyers-Rassias(UHR)stability.Ulam’s stability analysis plays an important role in various fields including numerical analysis,control theory,etc.[4–6,26–29,32,33,36,37,39–46,49,50,53–56,58–65,67–69].

Impulsive differential equations turned out to be the best tools for modeling physical problems which are subject to abrupt changes of state at a certain instant.These equations are suitable for describing biotechnology processes,biological systems,mathematical economy,population dynamics,medicine,pharmacokinetics,chemical energy,etc.[11,12,31,50].Due to these fruitful applications in different fields,impulsive differential equations have received considerable attention from researchers.

Ulam-type stability of impulsive differential equations was proved by Wang et al.[51]in 2012.They followed their own work and studied the UHR stability and generalized UHR stability for impulsive evolution equations on a compact interval[52].Recently,Agarwal et al.[1]studied the existence of causal functional evolution equations with respect to the Hausdorffmeasure of noncompactness.

The notion of time scales analysis has recently been attracting a lot of interest.This theory was introduced by Hilger[24]at the end of twentieth century as a means of unifying the difference and the differential calculus,and is now a well-established subject.For details on time scales,see[3,7,10,20–23,30,34,42–44,57,66].In 2010,Lupulescu and Zada[30]proved the fundamental concepts of linear impulsive systems on time scales.

Motivated by the work done in[1],in this paper,we present the existence,uniqueness(EU)and the stability of the solution of the following nonlinear causal evolution integro-delay dynamic system:

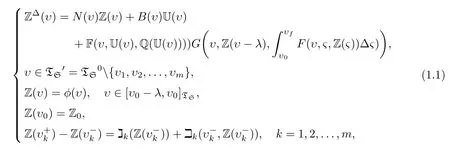
and of a nonlinear integro-delay dynamic system with integral impulses of fractional order of the form:

2 Preliminaries

3 Existence,Uniqueness and Ulam-Hyers Stability of the Solution of Equation(1.1)

In order to obtain EU and stability results for(1.1),we need to introduce the following assumptions:

4 Existence,Uniqueness and Ulam-Hyers Stability of a Solution of Equation(1.2)

In order to establish the EU and stability results of Equation(1.2),we introduce the following assumptions:

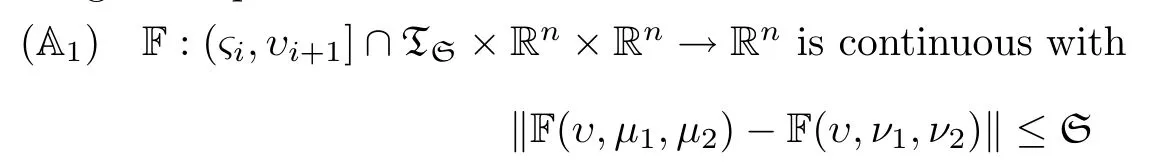
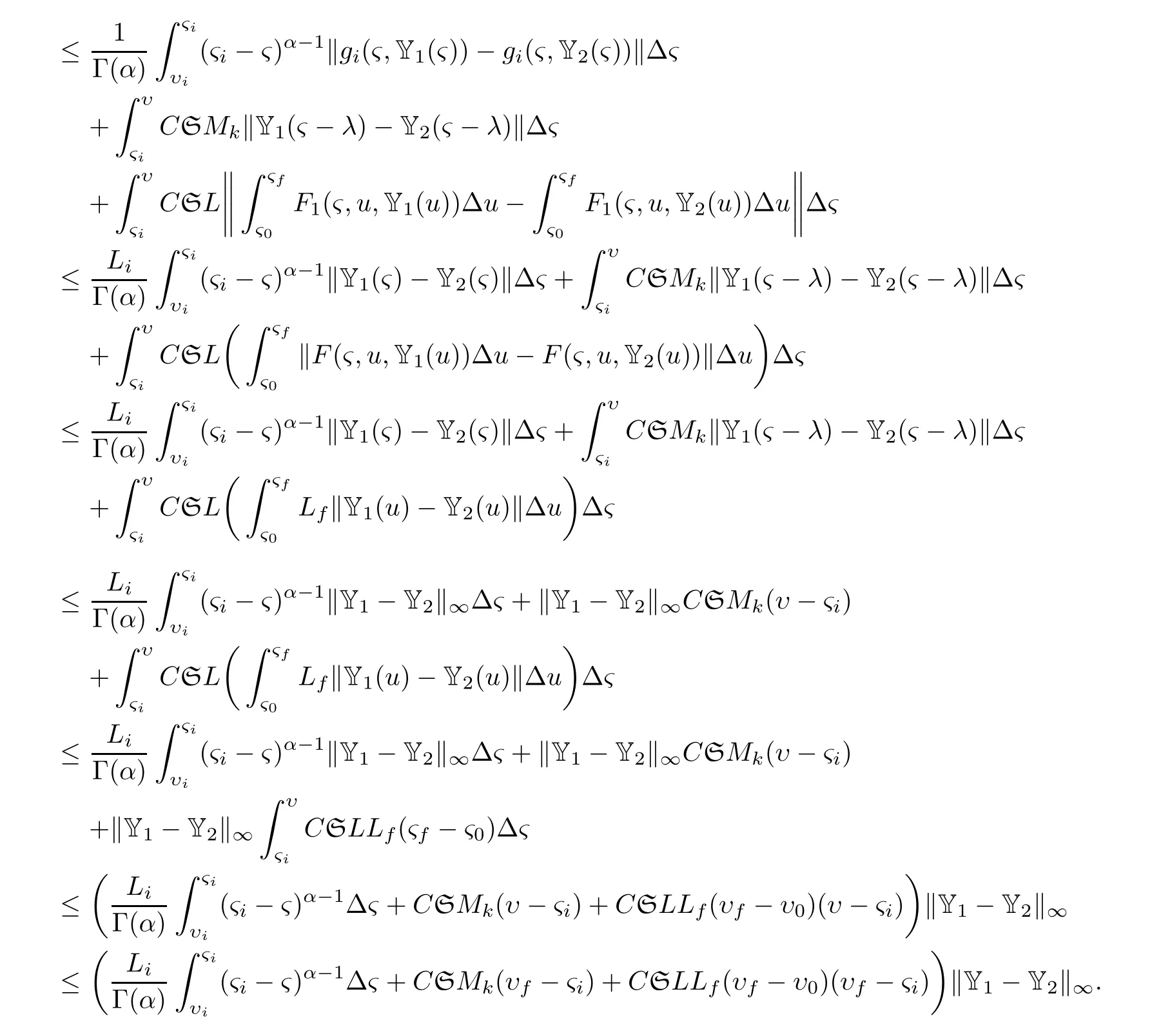
Utilizing(A5),the above,operator Λ is clearly strictly contractive on PC1(D,Rn),and hence it is a PO on PC1(D,Rn),so it has only one point,which is clearly the only one solution of(1.2)in PC1(D,Rn). □

Theorem 4.2If Assumptions(A1)–(A5)hold,then Equation(1.2)has UH stability on D.

ProofIf Y∈PC1(D,Rn)satisfies(2.3),then the unique solution of system

is

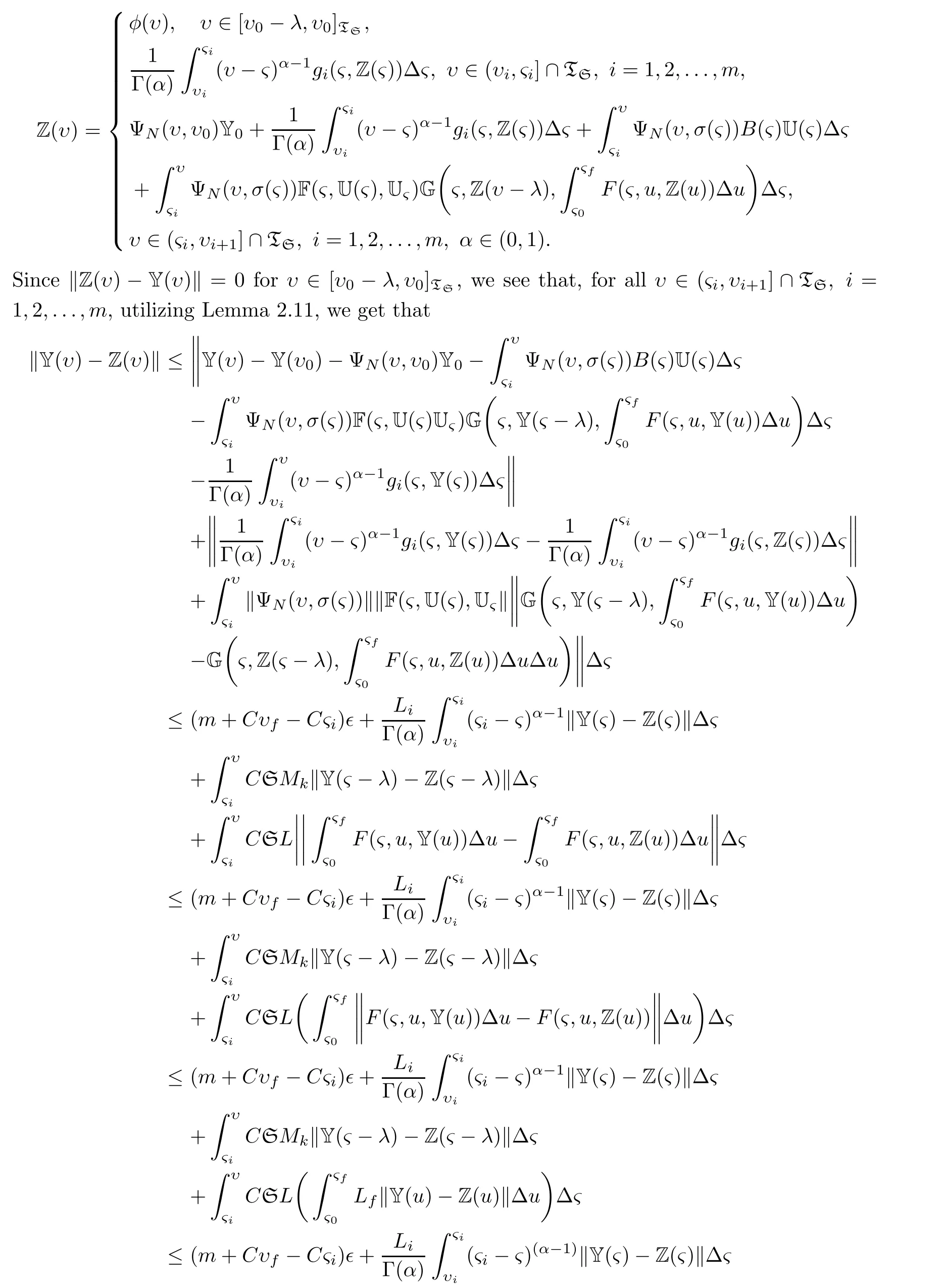
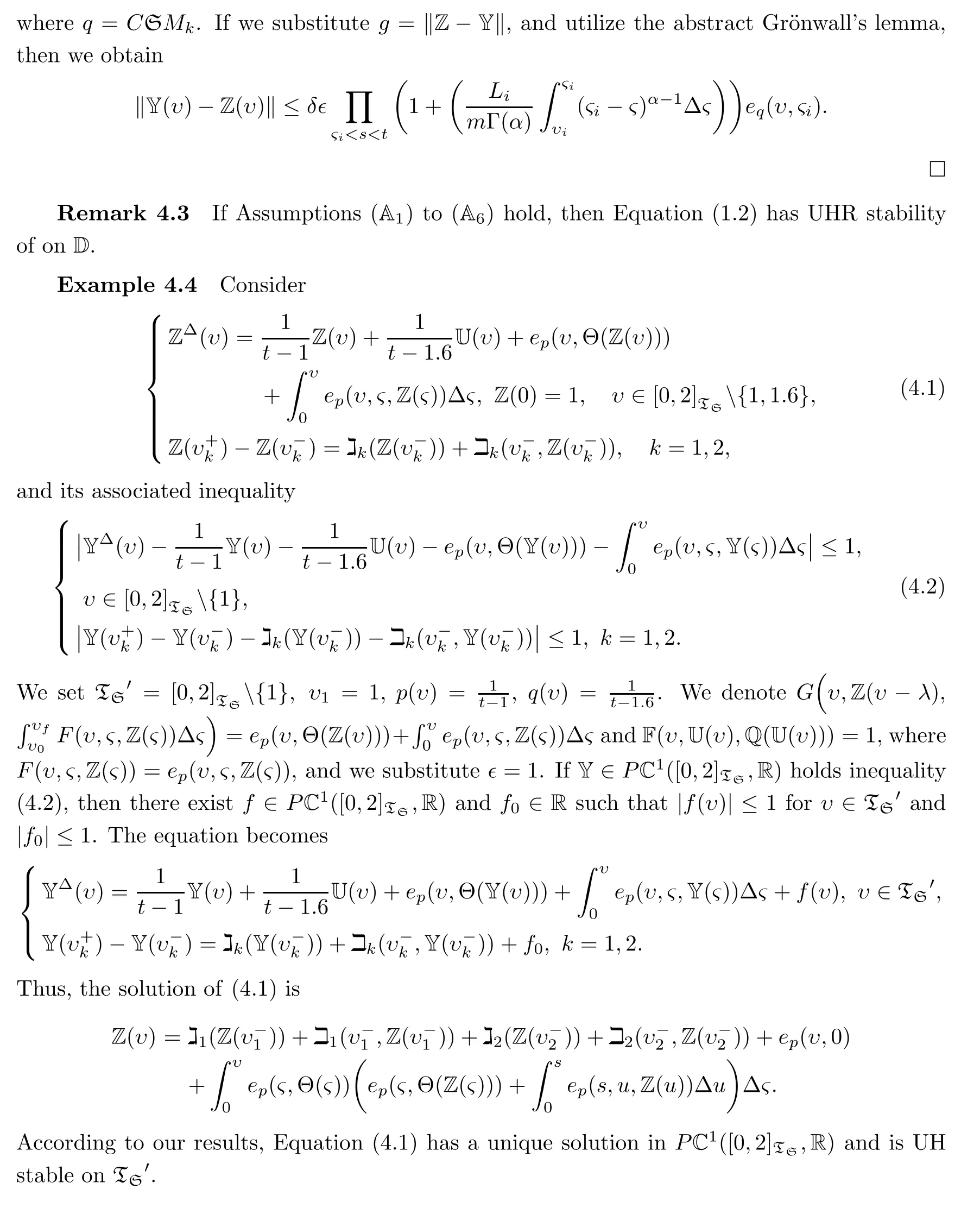
Conclusion

In this article,an attempt has been made to establish EU and stability results by using the FP method for(1.1)and(1.2).We established our results by using Lemma 2.7 and an abstract Gr?nwall’s lemma.When it is difficult to find the exact solution,then the notion of UH stability is fruitful;that is why,in approximation theory,our results are important.