基于ARIMA模型的極端事件下鐵路貨運量預測研究

孫 斌，陳思伶，杜麗慧

（1.中鐵四局集團建筑工程有限公司，安徽 合肥230022；2.華東交通大學經濟管理學院，江西 南昌330013）

由于我國的地理條件內陸深、范圍廣，鐵路在我國的物流發展中具有舉足輕重的地位[1]。鐵路貨運量是研究物流需求的重要指標之一，能夠為鐵路物流基礎建設和物流系統的合理規劃提供重要依據。鐵路工作的規劃需要獲取未來一定時期的鐵路客、貨運流量，科學準確的預測鐵路流量是鐵路規劃的前提和基礎，能獲取不同時間、空間區域的流量特征，為鐵路規劃提供全面、可靠的參考[2]。然而，在類似新冠疫情這樣的極端事件突發時，運輸量會呈現出一定的復雜性和不確定性，后續的抗疫工作也會給交通運輸業帶來較大影響，因此，準確的預測鐵路貨運量數據與變化趨勢對鐵路工作的開展有重要的參考意義。

劉月等通過對比考慮滯后期與不考慮滯后期的模型，證明了將滯后性引入吞吐量預測的重要性[3]；DAI在分析影響交通流量因素的基礎上，采用多元線性回歸方法預測交通流量[4]；黃慧瓊采用模糊線性回歸算法對交通流量進行預測，但這一方法不適合預測波動大的數據[5]；汪志紅等將改進的移動平均自回歸模型（ARIMA）應用于月度鐵路客運量的預測，分析了季節因素與節假日對鐵路客運量的影響[6]；賈學鋒利用灰色預測模型進行公路貨運量的預測研究，取得了較好的預測效果，實現了小樣本數據的貨運量預測[7]；原云霄等基于AR I MA模型實現了對公路物流指數的預測過程，并得到了比較好的擬合效果[8]；Kumar等將具有周期性的交通流實時數據處理擬合成參數模型，用季節ARIMA模型對短期交通流進行預測，但擬合程度較差，不適合短時交通流預測[9]；嚴雪晴，崔乃丹，劉夏，徐莉等用灰色預測模型對貨運量、交通流量進行預測[10-13]；江天河，邵夢汝等將神經網絡模型應用于客流量及貨運量的預測[14-16]；國內外學者對交通運輸流量進行了很多研究工作，形成了相對成熟的預測理論體系[17],但對于極端事件影響下鐵路貨運量的ARIMA模型預測沒有得到過驗證。

2020年2月，突發的新型冠狀病毒肺炎疫情短期內給我國經濟社會造成了較大沖擊，對各種方式的運輸都產生了影響。在疫情防控工作中，交通運輸業承受了巨大的壓力，直至五月份疫情逐步得到控制，經濟逐漸回暖[18]。分析和預測疫情對運輸工作的影響能為后續可能出現的風險做好應對準備。選用國家統計局2020年1—2月的鐵路貨運數據為訓練集，2020年3—10月的數據為測試集，尋求適當的ARIMA模型，并做出相關預測。選擇這次極端事件發生后2020年3—10月的鐵路貨運量進行ARIMA模型的預測驗證。運用工具為SPSSStatistics 26，將原始數據導入SPSS軟件，對數據進行差分、ARIMA建模、Ljung-Box檢驗等處理，最終輸出預測結果。

1 ARIMA模型

ARIMA模型屬于時間序列模型中的隨機性模型，將不同時間跨度的數據按照時間的先后順序排列而成，描述了數據樣本隨時間變化的分布和趨勢。美國學者Box和英國學者Jenkins在20世紀70年代提出了ARIMA模型，稱為移動平均自回歸模型，簡記為ARIMA（p，d，q）。其建模思想是將一個隨機時間序列用相應的數學模型進行分析研究，深入了解這些動態數據的內在聯系及復雜特性，從而進行最佳預測。

AR是自回歸，p為自回歸項，代表時序數據本身的滯后數；MA為移動平均，q為移動平均項數，代表預測誤差的滯后數；d為時間序列成為平穩序列所需要的差分階數。所謂ARIMA模型，是指將非平穩時間序列轉化為平穩時間序列，然后將因變量對它的滯后值以及隨機誤差項的現值和滯后值進行回歸所建立的模型。ARIMA模型根據原序列的平穩情況、回歸的內容不同分為移動平均過程（MA）、自回歸過程（AR）、自回歸移動平均過程（ARMA）以及ARIMA過程。如果時間序列既有趨勢變動，又有季節變動，就先要對序列進行n階差分消除趨勢性，再進行季節差分消除序列的季節性，差分步長應與季節周期一致，最終成為平穩序列。

2 ARIMA模型實證過程

2.1 正常數據預測

2.1.1 數據平穩性檢驗

近年來國民經濟快速增長，鐵路貨運量整體也呈現增長趨勢。同時受國家節假日及寒暑假的影響，其變化趨勢具有一定的周期性，如圖1所示，2010—2019年我國鐵路呈線性趨勢，并伴隨周期為12月的季節波動。利用SPSS軟件得到120個貨運數據樣本的自相關函數（ACF）和偏相關函數，如圖2所示，自相關和偏相關圖像都是拖尾的，并未衰減到0，因此數據序列是非平穩的。

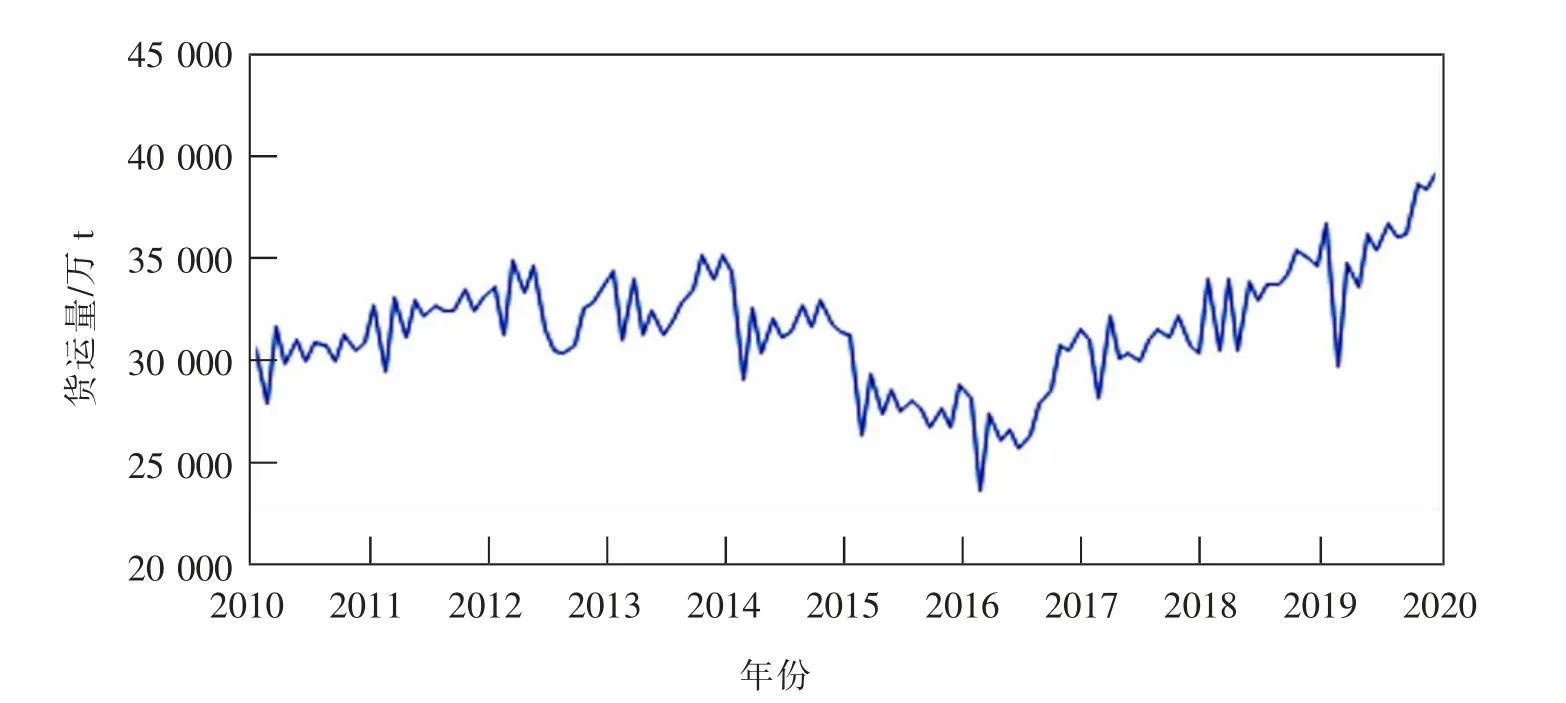
圖1 2010—2019年鐵路貨運量Fig.1 2010—2019 railway freight volume

圖2 原始數據的自相關、偏相關圖Fig.2 Autocorrelation and partial correlation of original data

2.1.2 數據預處理

為消除原始序列的趨勢信息，對數據樣本做一階差分。同時為了清除季節信息，對數據做周期為12月的一階季節差分，序列圖如圖3所示。分別做完一階差分和一階季節差分后作出自相關、偏相關函數圖，進一步驗證差分運算后的序列平穩性，如圖4所示。可以看出此時數據基本平穩。

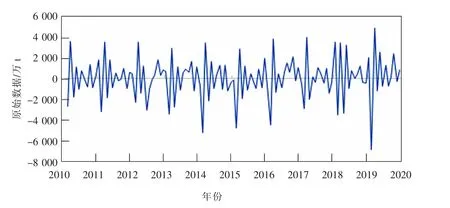
圖3 差分后的原始數據序列圖Fig.3 Sequence diagram of original data after difference

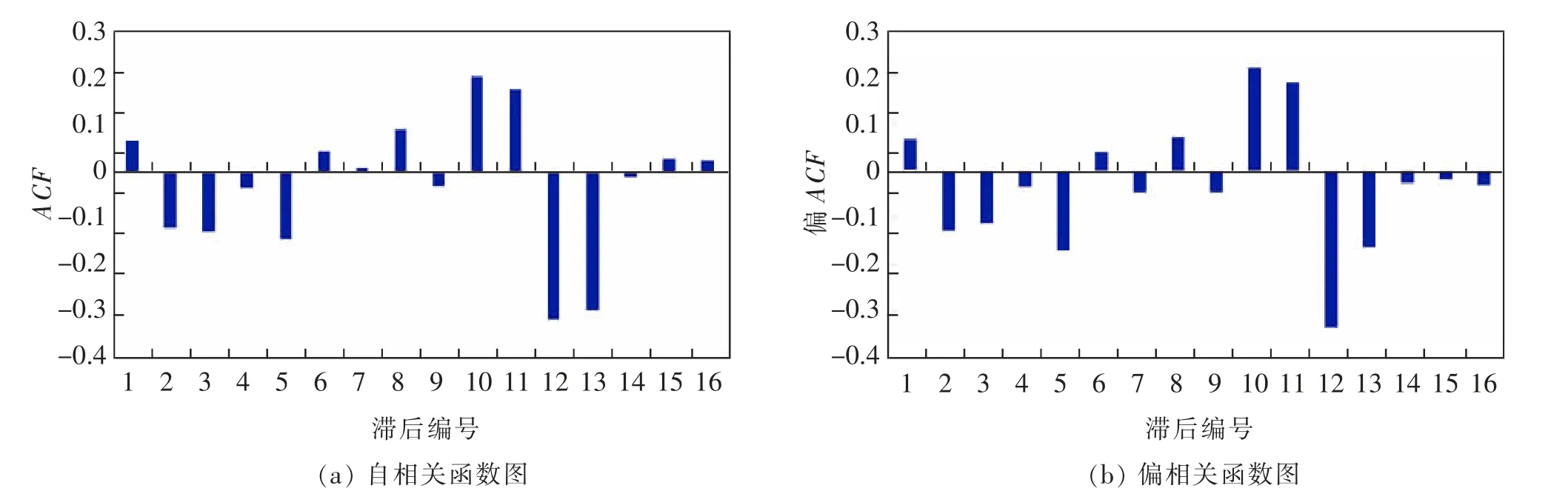
圖4 差分后的自相關、偏相關圖Fig.4 Autocorrelation and partial correlation after difference

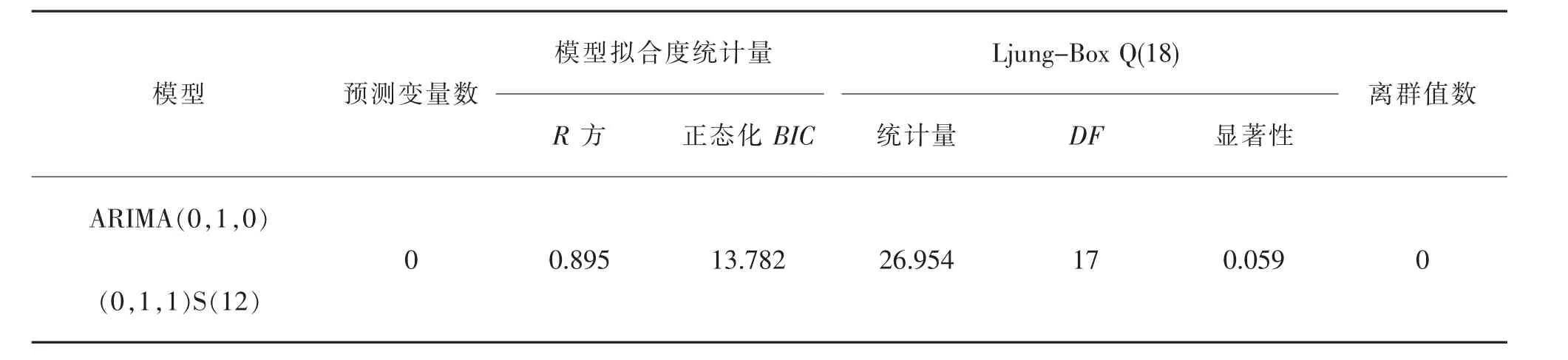
表1 ARIMA季節差分模型擬合度Tab.1 Fitting degree of ARIMA seasonal difference model

通過觀察圖4選擇擬合模型的參數為ARIMA（0，1，0）（0，1，1）S（12）模型。根據所選擇的模型進行擬合，結果如表1所示。從表中可以看出，模型平穩的R方為0.895，說明模型能解釋原來序列中89.5%的信息，Ljung-Box（楊-博克斯）統計量的值顯著，說明ARIMA（0，1，0）（0，1，1）S（12）模型擬合該時間序列數據樣本的效果比較理想。

2.1.3 模型預測

建立ARIMA（0，1，0）（0，1，1）S（12）參數模型，應用SPSS軟件對2020年1—10月鐵路貨運量進行預測（表2）。將預測數值與實際數值進行比較可以看出，2020年1—5月疫情期間的預測值與實際值的殘差較高，平均殘差為4 100.41。其中4月份的殘差最高，達4 980.31，5月的殘差最低，為2 790。觀察數據發現，雖然1—5月的預測殘差高，但總體的增減趨勢與真實值大致相同，這是ARIMA模型能夠捕捉時間序列季節特征的特性。隨著疫情的逐步控制，2020年6月起貨運量預測值的精度也隨之升高，6—10月的平均殘差為960.99，預測結果較接近。

表2 2020年正常數據預測值Tab.2 Predicted value of normal data of 2020

2.2 加入異常數據預測

在原始鐵路貨運量數據基礎上加入本次極端事件發生后2020年1—2月的異常數據，再次使用SPSS軟件進行ARIMA（0，1，0）（0，1，1）S（12）模型的預測實證，預測值為2020年3—10月，預測結果如圖5。可以看到，加入疫情發生后的異常數據預測的3—5月預測殘差較低，平均殘差為833.75，較正常數據預測結果的平均殘差下降79.65%。其中3月的殘差絕對值低至125.44，5月的預測殘差也較正常數據預測結果下降了1 000.63。6月份起疫情控制，經濟回暖，異常數據的預測精度逐漸下降，6—10月的預測殘差平均絕對值為3 889.83，是正常數據預測結果的4.05倍。

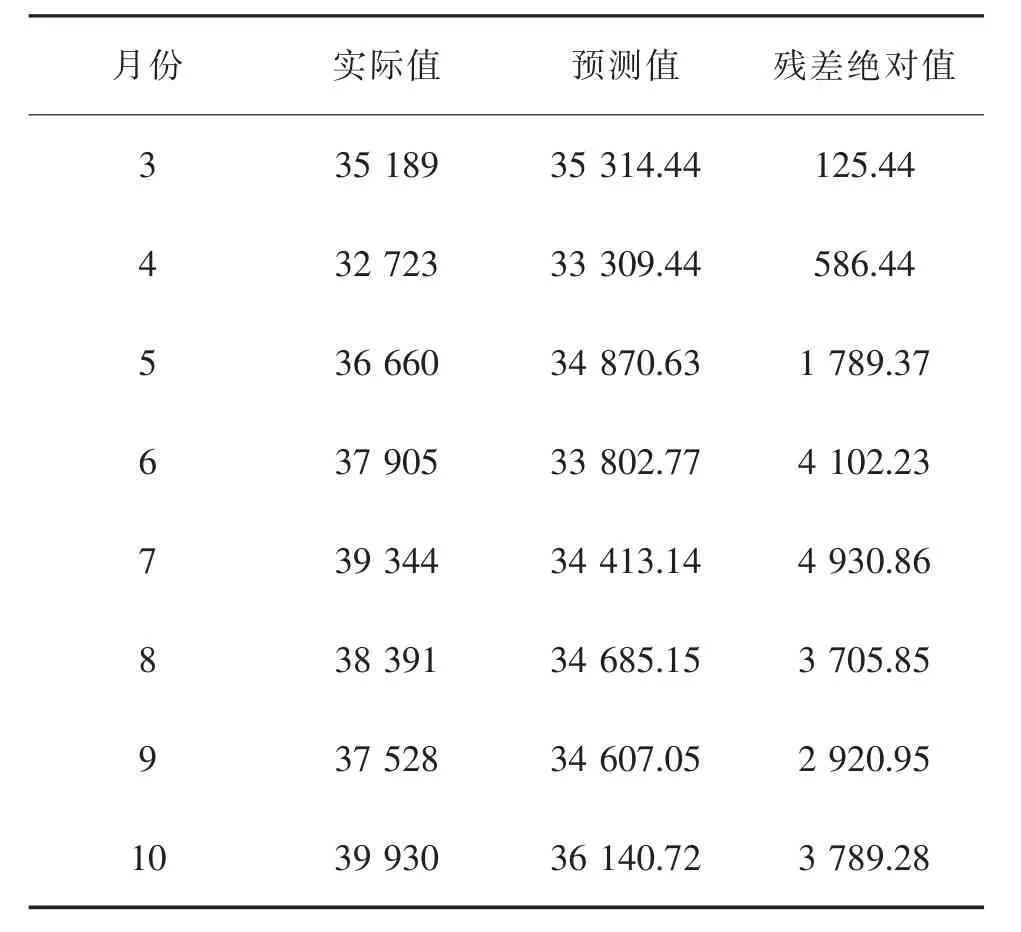
表3 2020年加入異常數據后預測值Tab.3 Predicted value after adding abnormal data

3 預測結果分析

通過對比正常數據的預測殘差和加入異常數據后的預測殘差可以發現，正常數據的預測結果在1—5月殘差較高，殘差平均絕對值為4 100.41，預測精度不理想；待疫情影響逐漸褪去、鐵路貨運情況恢復正常的6—10月區間，預測精確度較高，殘差平均絕對值為960.99，能夠準確預測。

加入2月份鐵路貨運量異常數據進行預測的結果在3—5月精確程度高，殘差平均絕對值為833.75，說明該參數模型能夠精準預測該區間的貨運量；而鐵路工作逐步恢復正常的6—10月區間預測殘差突升，從5月的1 789.37升高至6月的4 102.23，預測精度下降。

取加入異常數據預測結果的3—5月份，結合正常數據預測結果的6—10月份，可以得到較為精確的2020年3—10月預測值（圖5）。從圖5可以看出，預測結果較好的驗證了ARIMA模型在極端事件發生后異常值與正常值的預測能力。

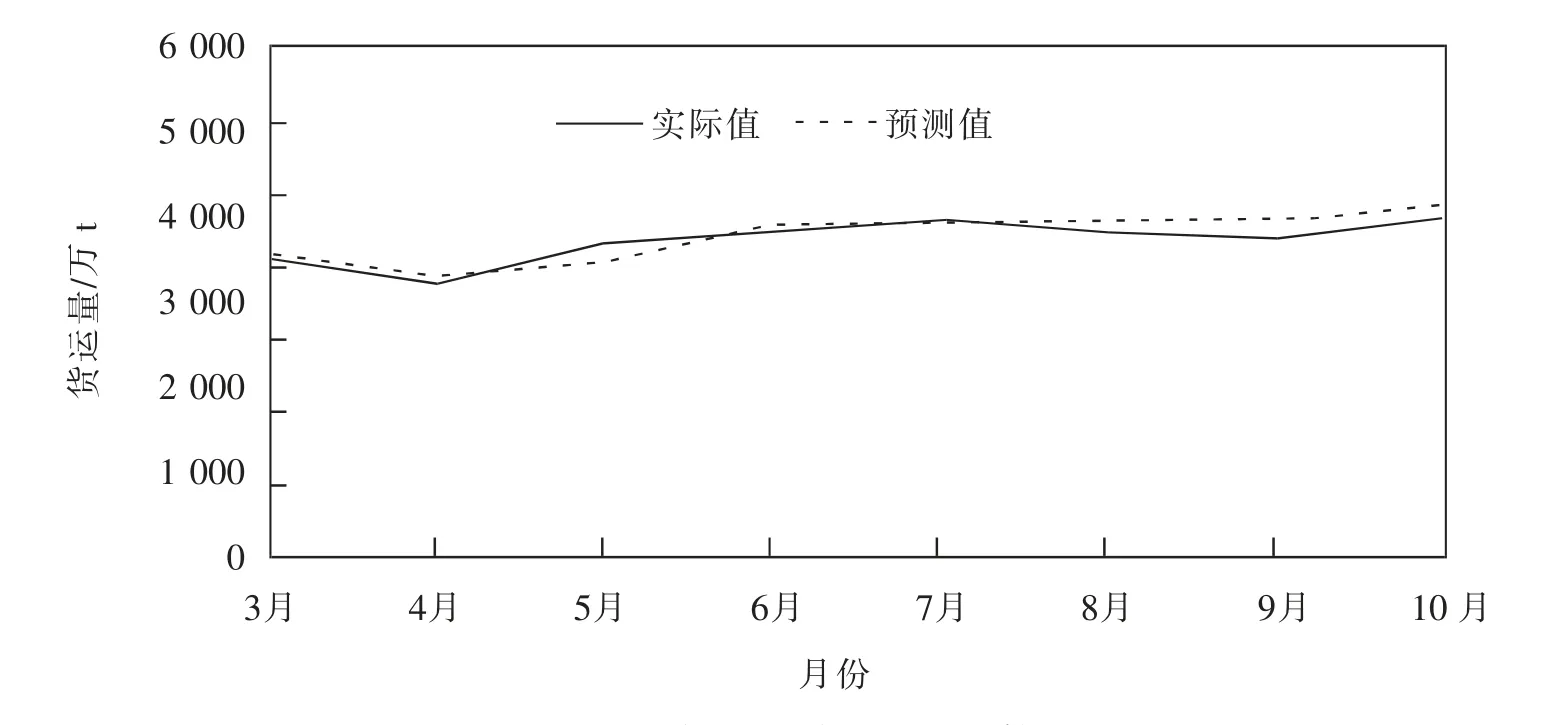
圖5 最終預測值與實際值比較Fig.5 Comparison of final predicted value and actual value

4 結論

類似新冠疫情的極端事件會從不同方面影響鐵路貨運量，準確的進行月度貨運量預測對鐵路部門的調度工作尤為重要。本文利用2010—2019年的鐵路貨運量歷史數據與疫情發生后2020年2月的異常數據構建ARIMA模型，對2020年3—10月的鐵路貨運量進行預測。

1）結果表明，原始數據加入極端事件發生當月的異常數據得到的預測值，與事件發生后、影響消退前的真實值較為接近，預測結果精確，驗證了ARIMA模型在極端事件影響下的預測能力。而正常數據的預測結果在極端事件的影響逐漸消退后預測精度也逐步恢復，仍然有參考價值。

2）疫情發生后，鐵路部門可以利用當月的異常數據結合歷史正常數據進行較短的區間預測；待疫情控制、影響逐漸消退，鐵路部門可以繼續使用正常數據得到的預測結果，這為鐵路的運輸組織方案及人員配備等提供了重要依據。