結合區間二型FRCM 與混合度量的兩階段信息粒化
邵麗潔,馬福民
(南京財經大學信息工程學院,南京 210023)
0 概述
信息粒化[1-2]是在問題求解空間中通過給定粒化策略將復雜數據轉化為信息粒集合的構造性過程。作為粒計算的前提和關鍵,信息粒化研究進一步推動了智能信息領域的理論創新,在知識發現、海量數據挖掘、復雜問題求解等領域具有廣泛的應用前景[1]。為解決模糊不可分的復雜問題,從而進行有效的問題分析及知識表示[3],PEDRYCZ 等人以顆粒的形式劃分模糊信息并根據現有依據形成“可信”粒子,提出了基于可信粒度準則的兩階段信息粒化框架[4-5]。第一階段通過無監督學習的聚類分析方法,由原始數據形成數據集結構的雛形;第二階段在監督模式下基于數據類簇構建信息顆粒,捕獲數據集的核心結構,從而構建更綜合和全面的粒度結構,使最后所生成顆粒原型的整體性能更佳[5]。
在兩階段粒化框架中,聚類既是粒化的手段,又是粒化的基礎。用于粒化的聚類算法大體分為硬聚類和軟聚類兩類。C-Means硬聚類(Hard C-Means clustering,HCM)[1,5-6]算法要求所有數據對象明確劃分到確定的類簇,因此,在處理交叉類簇的重疊區域時易產生大量誤分樣本而影響粒子質量。模糊C均值(Fuzzy C-Means,FCM)[7-8]是最常見的軟聚類算法,考慮到模糊隸屬函數設計的主觀因素,近年來粗糙C均值(Rough C-Means,RCM)[9]聚類算法得到快速發展。此后,將模糊集與粗糙集優勢互補的模糊粗糙C 均值(Fuzzy Rough C-Means,FRCM)[10]聚類算法也受到廣泛關注。為提高對不確定性問題的描述能力,文獻[11]將一般模糊集(稱之為一型)擴展到二型模糊集,以主、次兩級隸屬函數共同描述模糊語言的“模糊程度”,但時間復雜度大幅增加。文獻[12-13]通過默認次級隸屬度取常數1,將二型模糊集簡化為區間二型模糊集,以降低運算復雜度,這不僅增強了對不確定性信息的描述能力,而且也避免了算法的運算量呈指數級增長,同時還為邊界交叉的不確定數據在兩階段信息粒化下的聚類分析提供了新思路。
信息粒化框架的第二階段基于可信粒度準則構造綜合考慮覆蓋度和獨特性的粒化函數,得到形成“可信”信息顆粒的解決方案。根據粒化依據,通常設計與粒子樣本個數或權重呈正相關的函數來描述粒子的覆蓋度,而反映粒子語義的獨特性則正相反,其統一利用區間長度相關的非遞增函數進行度量。目前被使用較多的粒化函數有余弦函數[14]、指數函數[15-17]、基于區間比值的線性函數[18-20]、基于區間與衰減參數的積分函數[21-23]等。文獻[15-17]利用指數函數表述粒子的獨特性,函數在X軸正半軸區域的變化趨勢充分反映了粒子隨區間長度增加語義不斷衰減的非遞增特性,通過指數系數α控制粒子的粒度大小,可實現不同層次的粒化。然而,包括指數函數在內的上述所有函數在表述粒子獨特性時,都只考慮了粒子區間大小而忽視了粒子內部數據的空間分布和疏密程度,不能較好地描述粒子的獨特性,直接影響了所生成粒子的質量。
為解決多類簇交叉且分布不均衡數據的信息粒化問題,本文提出一種結合區間二型FRCM 聚類與混合度量的兩階段信息粒化算法。在第一階段,依據可信粒度準則,基于區間二型FRCM 算法對不平衡數據進行聚類分析,在有效提升分析精度的同時,獲取類簇形式的初始信息粒;在第二階段,采用混合度量方法,以數據分布的疏密程度表述粒子內部的空間結構,以區間大小刻畫粒子的區域范圍,從而在充分描述粒子特性的同時,清晰體現粒子結構,最終獲得客觀的劃分方案,形成合理的粒子區間。
1 相關知識
1.1 基于模糊集與粗糙集的C 均值聚類
在可信粒度準則的兩階段粒化框架中,聚類分析不僅被視為構建粒度原型的先決條件,而且還被作為揭示數據結構和構建信息顆粒的事實標準。基于模糊集和粗糙集的聚類分析可在缺乏先驗知識的前提下對含有不確定信息的數據進行初步分析。
1.1.1 模糊粗糙C 均值算法
文獻[10]融合兩種軟計算方法,引入粗糙集理論中上下近似的概念和模糊集理論中模糊隸屬度的概念,將歸屬關系模糊的數據樣本劃入類簇的邊界區域,將歸屬關系明確的數據樣本劃入類簇的下近似區域,進而提出模糊粗糙C 均值(FRCM)算法。考慮到類簇邊界區域的不確定性,該文作者認為每個數據樣本對類簇與類簇中心的影響程度都不同,因此,使用取值在0 到1 之間的模糊隸屬度進行計算,如式(1)所示:

其中,C為類簇個數,dij為數據樣本xj與類簇中心vi的歐式距離,m為模糊化系數。在劃分數據樣本與類簇間的歸屬關系時,若存在類簇Ck滿足|dij-dkj|<ξ,則將xj劃入類簇Ci的邊界集,否則將xj劃入類簇Ci的下近似集。模糊隸屬度的計算公式定義為:
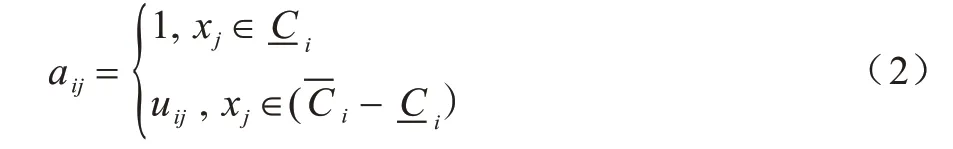
1.1.2 區間二型模糊C 均值算法
文獻[11]在針對復雜不確定問題建模時,研究模糊化系數m對模糊邊界的影響,提出了區間二型模糊C均值(Interval Type-2 Fuzzy C-Means,IT2FCM)聚類算法。該算法考慮類簇規模,通過使用主、次兩級模糊隸屬函數更準確地描述了不確定性問題的模糊程度,增強了對高階模糊不確定問題的描述能力[12-14]。為解決時間復雜度指數級增長的問題,默認次級模糊隸屬度為1,將區間函數轉化為數值區間。在IT2FCM 算法中,二型區間模糊隸屬度的計算公式如下:
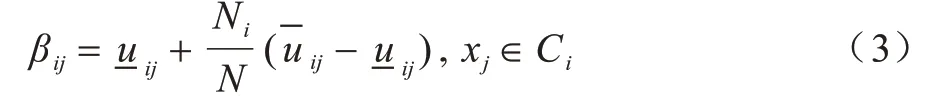
其中,Ni為類簇Ci的樣本規模,N為數據樣本總數。先通過式(1)計算兩個模糊化系數對應的模糊隸屬度,再根據最值情況判斷左右區間值,如式(4)和式(5)所示:
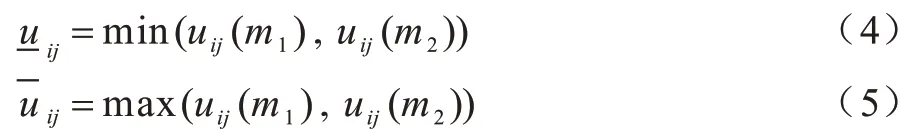
1.2 可信粒度準則
PEDRYCZ 等人提出的可信粒度準則[6,24]基于提供的實驗證據形成有意義的信息顆粒,被作為一種有效的數據粒化手段。依據數據本身的特性,可信粒度準則兼顧了粒子形成過程中的覆蓋度與獨特性,同時包含了優化的目標函數。
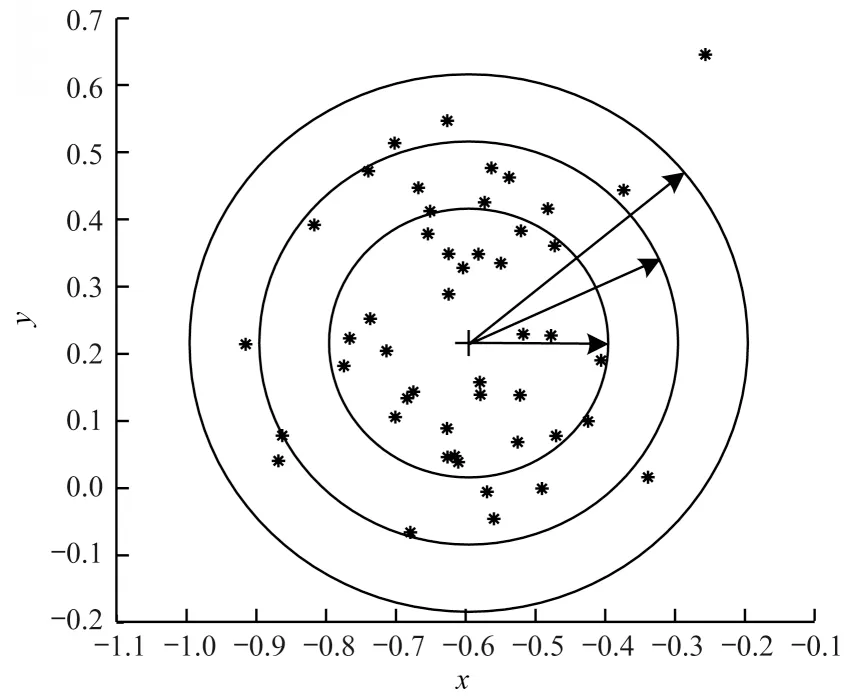
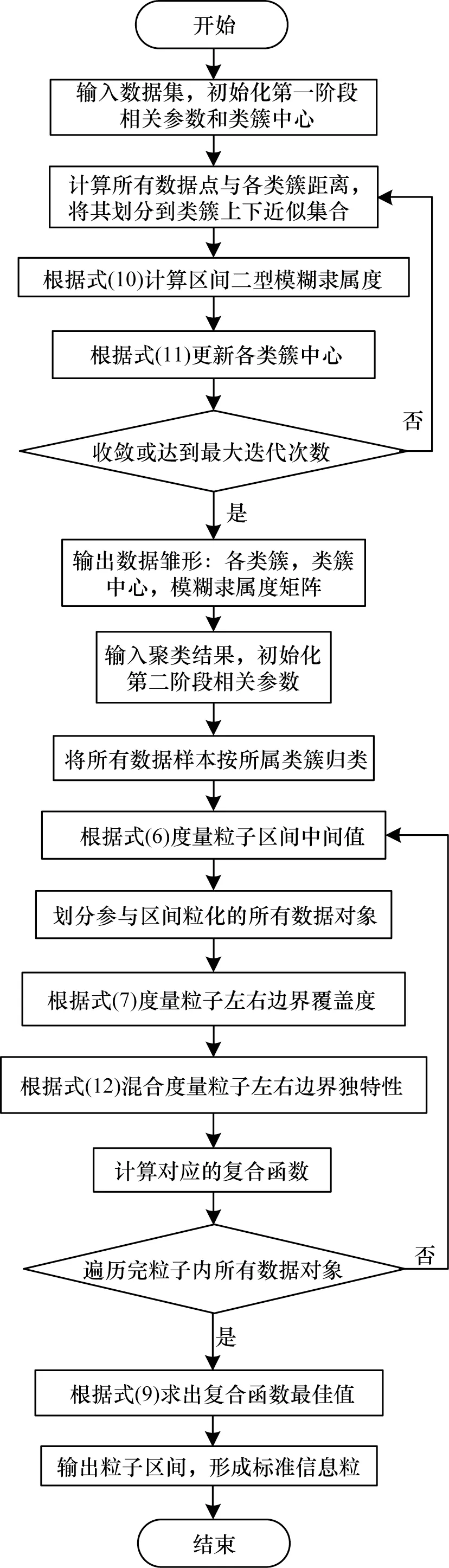
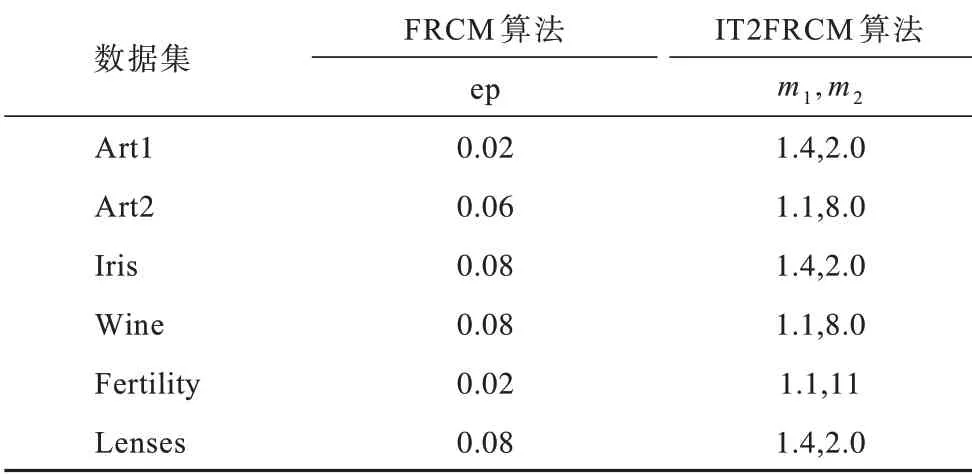
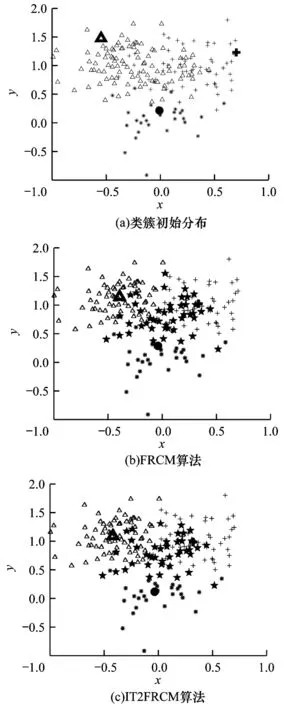
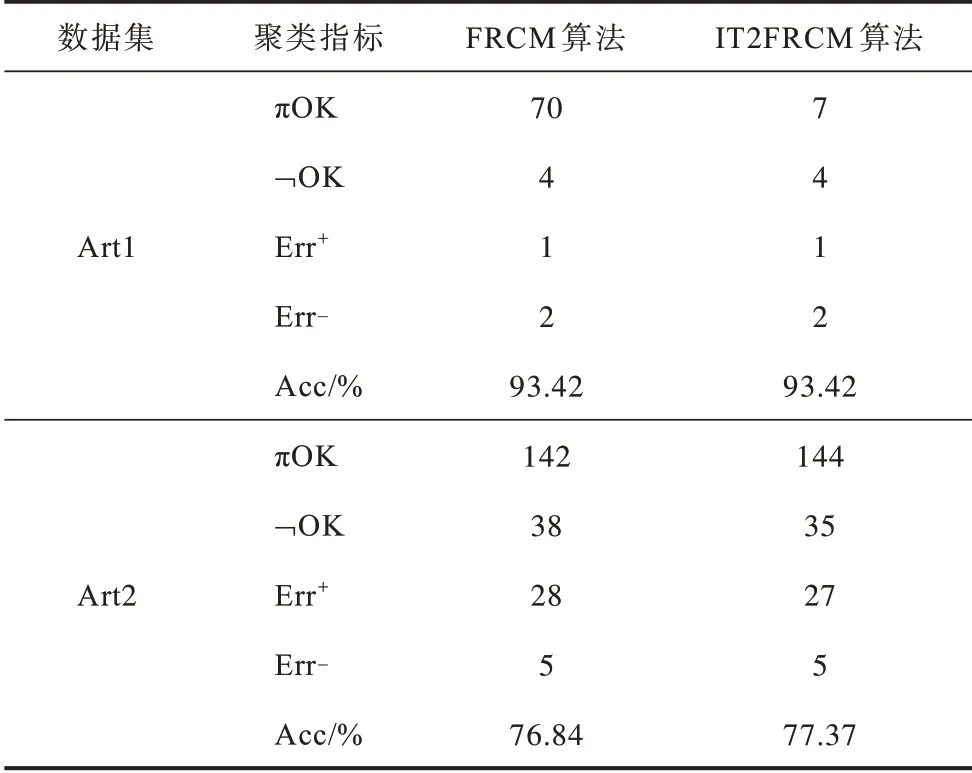
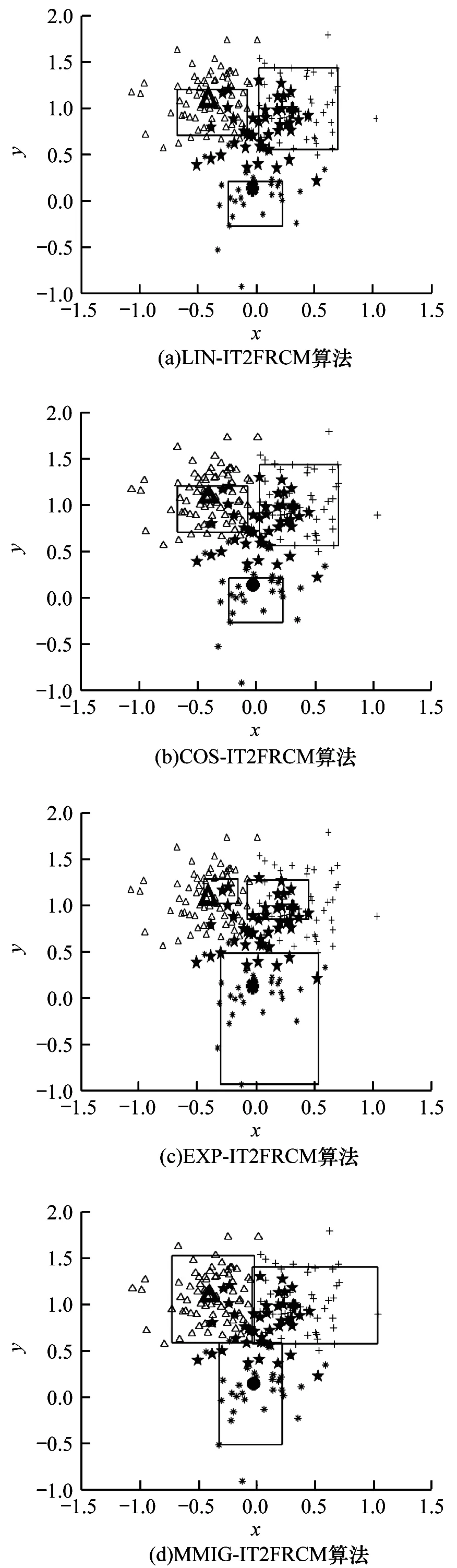
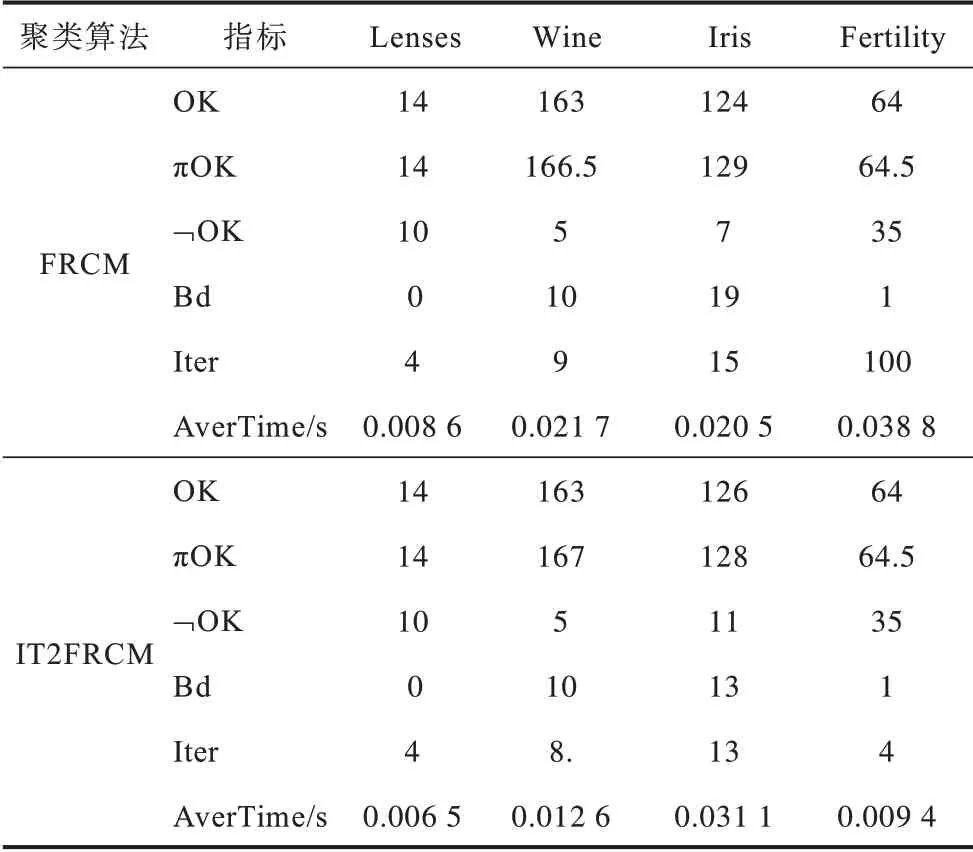
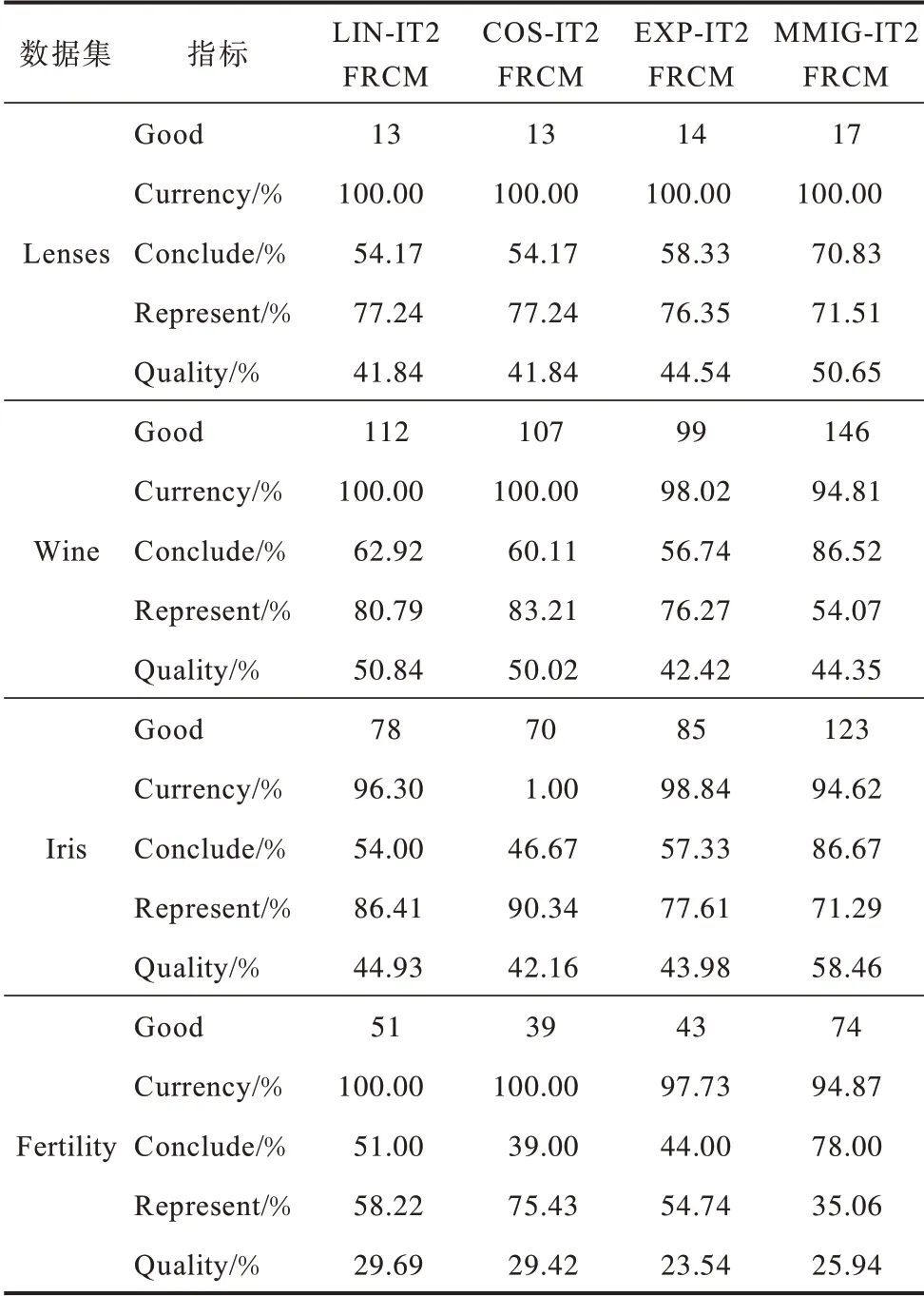
基于可信粒度準則,類簇X={x1,x2,…,xM}生成以區間[a,c,b]表示的某信息粒Ω,如圖1 所示。其中,M為各類簇劃入粒子區間參與粒化的數據樣本個數,M=kN,0 圖1 模糊粒子區間Fig.1 Interval of fuzzy granule 對所有數據樣本按權重大小進行升序排列,得到新簇X′,并將最大權重對應的數據樣本設為粒子區間的中間值c[24]: 定義1粒子的覆蓋度[24]表示粒子的顆粒大小,其揭示了粒子具有的合理證據。在模糊劃分過程中,一定范圍內粒子區間越大,包含的數據樣本越多,越有利于提取合理可信的粒子語義。描述覆蓋度的粒化函數g反映數據的遞增特性,常用權重表示: 定義2粒子的獨特性[24]與粒子語義有關,可揭示粒子所含信息的抽象程度。在模糊劃分過程中,一定范圍內粒子區間越小,包含的數據樣本越少,越有利于提取清晰的粒子語義。獨特性粒化函數f反映數據的非遞增特性,常用指數函數[15-17]表示: 定義3目標函數反映粒子的整體質量。由于粒子的兩大特性是相互沖突的,因此把代表粒子覆蓋度和獨特性的粒化函數組合為復合公式,并利用argmax()函數求解目標函數的最大值,將尋找最佳粒子邊界的問題轉化為具體的優化問題,一般表現形式為[24]: 對于類簇邊界交叉重疊的數據集,類簇間規模的不均衡性對聚類分析的結果影響較大。當兩個類簇的規模相差較大時,小規模類簇更容易受到邊界區域的影響,且聚類中心點更易向規模較大的類簇偏移[14]。不同于傳統的模糊隸屬度量,區間二型模糊集合理論的隸屬度在描述不均衡類簇邊界交叉的不確定信息時具有明顯的優勢,IT2FCM 算法也被用于不均衡類簇數據的聚類分析[12-14]。IT2FCM 算法雖然一定程度上體現了不同區域數據樣本的分布差異,但一些明確屬于某個類簇的數據樣本仍然需要參與其他類簇的隸屬度量計算,未對具有不同歸屬程度的數據樣本進行有區別的處理,會影響不均衡類簇數據聚類分析精度的提升,同時也會增加計算復雜度。 為削弱類簇規模不均衡問題的不利影響,本文在IT2FCM 算法的基礎上,引入粗糙集理論中上下近似的概念,考慮到不同區域的數據樣本對類簇聚類的貢獻度有明顯差異以及計算所有數據樣本模糊隸屬度的時間成本,只對邊界區域的數據樣本進行二型區間模糊度量,而下近似區域數據樣本取固定隸屬度1,從而得到適用于多類簇交叉且分布不均衡數據的IT2FRCM 算法,將其作為粒化第一階段的聚類分析方法。 在IT2FRCM 算法中,模糊隸屬度計算公式[14]如下: 相應的類簇中心迭代計算公式為: IT2FRCM 算法在計算數據樣本的權重時綜合考慮了類簇的規模與空間分布信息,按規模大小自適應獲得相對的加權系數,有效削弱了邊界區域對聚類的影響,可避免類簇中心向邊界區域嚴重偏移。 基于IT2FRCM 聚類所形成的基礎信息粒,在描述粒子成粒依據時,保留數據樣本與類簇歸屬關系的模糊隸屬度,以區間范圍內數據樣本的權重和來度量粒子覆蓋度[24]。傳統的粒化算法對于粒子獨特性的度量多基于余弦函數[14]、指數函數[15-17]和線性函數[18-20]等衰減函數,其將粒子區間大小看作是影響粒子獨特性的唯一因素。然而,由圖2 所示基礎信息粒的區間劃分圖可知,在以類簇形式存在的基礎信息粒中,數據樣本(以*表示)的分布并不均勻:越靠近類簇中心(以+表示),分布的數據樣本越密集;越靠近類簇邊界,分布的數據樣本越稀疏。當粒子區間長度(以→表示)均勻增加時,劃入粒子區間內數據樣本的個數往往會受到類簇中數據樣本分布的影響而不均勻增加,從而導致粒子的獨特性也發生不均衡變化。 圖2 基礎信息粒的區間劃分圖Fig.2 Interval partition graph of basic information granule 由此可知,粒子的獨特性不僅與區間大小有關,而且還受到數據樣本空間分布的影響。雖然傳統描述粒子獨特性的衰減函數一定程度上滿足了隨粒子區間增大粒子獨特性減小的成粒原理,但簡單的區間數值忽視了粒子內部數據樣本的空間分布與疏密程度等因素對粒子特性的影響,不能很好地概括粒子內部的結構與性質。因此,區別于參數版可信粒度準則關于粒子獨特性的度量方式,本文綜合考慮區間與密度兩大因素,重新設計描述獨特性的指數函數,將粒子獨特性的表達式改進為: 其中,指數的分子表示粒子某區間范圍內所有數據樣本到均值中心c的距離和,分母表示xj作為某邊界點時粒子內部數據樣本總數,分式部分為粒子內部數據樣本與類簇中心的平均距離,反映了粒子內部數據樣本分布的疏密程度。為兼顧粒子區間與密度兩者對粒化的影響,避免單個因素過于片面地反映粒子的成粒情況,式(12)改進原有的指數函數,以乘積的形式結合密度與區間這兩個因素,使之共同表述粒子的獨特性。區間大小作為系數,直接影響粒化函數指數部分的乘積大小,從而控制函數變化的速率。指數函數的函數結構不僅體現了空間內數據樣本的分布特點,而且函數值的變化也符合數據樣本分布越密集則粒子結構越緊湊的成粒原理。因此,在基于可信粒度準則的粒化過程中,綜合考慮區間與密度來度量粒子獨特性,可使粒子區間的劃分更合理,使生成的標準信息粒更具有代表性。 為解決分布不均衡數據的信息粒化問題,本文基于IT2FRCM 聚類算法,以類簇的形式表示基礎信息粒,并通過改進參數版可信粒度準則下描述粒子獨特性的粒化函數,提出結合IT2FRCM 與混合度量的兩階段信息粒化算法MMIG-IT2FRCM,算法流程如圖3所示。 圖3 MMIG-IT2FRCM 算法流程Fig.3 Procedure of MMIG-IT2FRCM algorithm 算法的具體執行步驟如下: 算法MMIG-IT2FRCM 輸入數據集 輸出C個信息粒子 第一階段執行IT2FRCM 聚類算法。 步驟1設置并初始化相關參數,隨機選取類簇中心,設置相對距離閾值ep、最大迭代次數Iter 和模糊化系數m、m1、m2。 步驟2根據每個數據樣本xj與類簇Ci的位置關系,將其劃分到對應類簇的上、下近似區域。 步驟3依據式(10)計算所有邊界區域數據樣本與所屬類簇的模糊隸屬度hij。 步驟4依據式(11)更新每個類簇的中心vi。 步驟5若各類簇中心不再發生變化或已經達到設定的最大迭代次數,算法終止,否則返回步驟2重新進行迭代計算。 第二階段基于IT2FRCM 聚類結果進行信息粒化。 步驟1初始化粒化抑制參數λ,將所有數據樣本按所屬類簇歸類。 步驟2將類簇中心vi作為信息粒的中心賦值給c,并根據類簇中數據樣本的最值情況判斷類簇左右邊界范圍內可參與粒化的數據樣本xj。 步驟3將每個參與粒化的數據樣本xj作為潛在的粒子邊界點,根據式(7)和式(12)計算信息粒子的CCov(Ω)和SSpe(Ω)。 步驟4依據式(9)選取粒子左邊區域、右邊區域中粒子覆蓋度和獨特性乘積最大的樣本點,得出該維度下的粒子邊界。 步驟5確定信息粒子在各維空間下的左右邊界后,輸出信息粒子。 MMIG-IT2FRCM 算法在第一階段IT2FRCM 聚類時,其時間復雜度由距離矩陣計算的時間復雜度O(NC)、隸屬度矩陣計算的時間復雜度O(NC)和簇中心更新的時間復雜度O(NC)三部分組成。由于數據樣本總數N一般遠大于類簇個數C,因此算法聚類階段的時間復雜度為O(N)。第二階段信息粒化的時間復雜度則由所有數據樣本歸類的時間復雜度O(N)、粒子覆蓋度、獨特性及目標函數計算的時間復雜度(皆為O(k2N2))、最大目標函數值查找的時間復雜度O(kN)三部分組成。因此,粒化算法耗費的時間復雜度為O(k2N2),其中,k為常數,MMIG-IT2FRCM 粒化算法的整體時間復雜度為O(N2)。 相較于傳統參數版可信粒度準則下基于指數函數、線性函數或余弦函數粒化算法的時間復雜度O(N2),本文提出的MMIG-IT2FRCM 粒化算法時間復雜度沒有明顯增加。 為驗證MMIG-IT2FRCM 算法的有效性,選取人工數據集和多組UCI標準數據集進行實驗。首先對比分析IT2FRCM 和FRCM 聚類,然后對基于這兩種聚類的4個粒化算法進行對比實驗,驗證本文MMIG-IT2FRCM粒化算法的性能優勢。實驗環境如下:CPU 為Intel?CoreTMi5-4210H,內存為8 GB,操作系統為Windows10。 為保證實驗的公平性,使用隨機算法確定各數據集的初始聚類中心,同一數據集下所有聚類算法采用相同的初始聚類中心。相對距離閾值ep 隨不確定區域的增大而增大,以0.02 為間隔取0 到1 之間的最優參數取值。實驗時,模糊化因子m1、m2在1.1到11之間取經驗最佳區間值,抑制參數λ根據經驗設置為0.7,控制粒度大小的參數α取常規值1。相關參數取值見表1。 表1 不同數據集下2 種聚類算法的參數設置Table 1 Parameters setting of two clustering algorithms on different datasets 按照正態分布隨機生成3 個分別包含25 個、31 個和20 個數據樣本的類簇作為人工數據集1(Art1),按照正態分布隨機生成3 個分別包含30 個、60 個和100 個數據樣本的類簇作為人工數據集2(Art2)。為明顯區別于人工數據集1,通過控制正態分布的參數方差,使得人工數據集2 的類簇區域重疊情況更嚴重,類簇規模不均衡的特征也更明顯。Art2 數據集下FRCM 和IT2FRCM 算法的聚類效果如圖4 所示,其中,加粗且形狀較大的幾何圖形表示對應類簇的中心,星形表示對應類簇誤劃分到其他類簇的數據樣本。分析圖4 中不同規模且重疊情況不同的3 個類簇的聚類結果可知,采用IT2FRCM 聚類算法得到的聚類中心更為理想。 圖4 Art2 數據集下2 種聚類算法的聚類效果Fig.4 Clustering effects of two clustering algorithms on Art2 database 對2 種聚類算法的聚類指標進行對比,如表2所示。其中:πOK 表示類簇下近似集中聚類正確的樣本數加上類簇邊界集中聚類正確的樣本數與重疊系數的乘積最后所得的樣本數;?OK 表示類簇下近似集中聚類錯誤的樣本數;Err+表示多數類類簇被錯誤劃分到少數類類簇下近似集樣本數;Err_表示少數類類簇被錯誤劃分到多數類類簇下近似集樣本數;Acc 表示聚類精度,即聚類正確樣本數占樣本總數的比例。由表2 可知,在Art1 數據集上,根據聚類指標值無法直接判斷2 種聚類算法的優劣,而在類簇規模差異大且重疊情況更嚴重的Art2 數據集上,使用IT2FRCM 聚類算法取得了更好的聚類性能,這充分說明IT2FRCM 算法對數據分布不均衡的多類簇交叉數據集具有很好的適應性。 表2 人工數據集下2 種聚類算法的聚類指標Table 2 Clustering indicators of two clustering algorithms on artificial datasets 在第二階段,對基于IT2FRCM 算法的聚類結果實現信息粒化。實驗中,分別以線性函數(LIN)、余弦函數(COS)、指數函數(EXP)和本文所提出的混合度量函數(MMIG)作為不同的獨特性粒化函數,從而形成LIN-IT2FRCM、COS-IT2FRCM、EXP-IT2FRCM 和MMIG-IT2FRCM 這4 種粒化算法進行對比實驗。圖5 為Art2 數據集上4 種粒化算法所得到的粒化結果。其中,黑色矩形框是由粒子左、右邊界點形成的二維區間。黑色矩形框越大,表明粒子顆粒越大,越難提取有效的粒子語義,同時也表明粒子內部的數據樣本越多,包含的證據越充分、合理。由圖5 可知,本文提出的MMIG-IT2FRCM 粒化算法所形成的粒子區間相較于其他3 種粒化算法覆蓋了更多的數據樣本,其形成的粒子區間包含了更為充分的實驗證據。 圖5 Art2 數據集下4 種粒化算法的粒化效果Fig.5 Granularity effects of four granulation algorithms on Art2 database 在規模不均衡、空間分布明顯不同的2 個人工數據集下對4 種粒化算法的粒化指標進行對比,如表3 所示,其中:Good 為歸類正確數,即聚類正確的樣本個數;Currency 為歸類正確率,表示粒子內部所有數據樣本中歸類正確的數據樣本所占的比例;Conclude 為覆蓋率,表示粒子覆蓋范圍;Represent 為獨特性指標,反映粒子群的代表性;Quality 反映生成粒子的質量,是粒子群整體質量的最終評判標準。分析表3中各項粒化指標可知,MMIG-IT2FRCM 粒化算法在粒子聚類正確數、粒子整體質量和粒子的覆蓋度與獨特性等重要指標上均取得了最佳值。相較于其他3 種粒化算法,該算法具有明顯的性能優勢,得到的粒子群整體質量更好。 表3 人工數據集下4 種粒化算法的粒化指標Table 3 Granulation indicators of four granulation algorithms on artificial datasets 選取4 個標準的UCI 數據集Lenses、Wine、Iris、Fertility 進行實驗分析。小數據集Lenses 的3 個類簇各有4 個、5 個 和15 個數據樣本。Wine 數據集的3 個類簇各有59 個、78 個、41 個數據樣本。Iris 數據集的3 個類簇各有50 個樣本。Fertility 數據集的2 個類簇各有88 個和12 個數據樣本。數據集Iris、Wine 數據樣本分布均勻,Lenses 數據樣本幾乎不交叉。3 個數據集體現了不同的類簇交叉重疊程度,即Iris 4 個UCI 標準數據集在2 種聚類算法下的實驗結果如表4所示。其中:OK 為位于類簇下近似區域且聚類正確的樣本數;Bd為邊界區域的樣本個數;Iter為算法的迭代次數;AverTime 為平均時間。從表4 可以看出,除規模一致、均勻分布的Iris數據集外,其他規模差異大且非均勻分布的數據集耗費在IT2FRCM 聚類算法中的時間復雜度遠低于FRCM 聚類算法。在對類簇規模差異大且樣本點分散的Fertility 數據集聚類時,IT2FRCM 算法只迭代了4次就快速收斂,而FRCM 算法達到迭代次數上限后,被迫停止算法,時間復雜度很高。因此,綜合對比聚類正確數、迭代次數和平均時間等聚類指標可知,對于多類簇交叉且數據不均衡分布的數據集,IT2FRCM 算法在迭代運行過程中能夠實現快速收斂和準確分類。 表4 UCI 數據集下2 種聚類算法的聚類指標對比Table 4 Clustering indicators of two clustering algorithms on UCI datasets 4 個UCI 標準數據集下4 種粒化算法的實驗結果如表5 所示。可以看出,MMIG-IT2FRCM 粒化算法在歸類正確數、粒子覆蓋度和獨特性指標上均取得了最佳值。分別對比4 個UCI 數據集下4 種粒化算法的歸類正確數可知,本文提出的MMIG-IT2FRCM粒化算法生成的信息粒子內部聚類正確的數據樣本數更多,提取的粒子信息可用性強。分析粒子兩大特性可知,MMIG-IT2FRCM 粒化算法在Lenses、Wine、Iris、Fertility 數據集上覆蓋度取值明顯高于相同數據集下其他3 種粒化算法中覆蓋度的最佳值,可見MMIG-IT2FRCM 粒化算法生成的信息粒粒子區間更大。同時,MMIG-IT2FRCM 粒化算法在4 個標準數據集下獨特性取值明顯低于相同數據集下其他3 種粒化算法中的最佳值,反映了基于該粒化算法的粒子結構更為緊湊,更利于提取清晰的粒子語義。隨著粒子區間范圍擴大,會有更多邊界區域的誤分樣本被劃入粒子區間,因此,MMIG-IT2FRCM粒化算法在Wine、Iris、Fertility 數據集上的歸類正確率略微遜色于其他3 種粒化算法,但粒子覆蓋度和獨特性兩大特性指標得到明顯提升,與經典的EXPIT2FRCM 粒化算法相比,其正確率的取值仍然控制在合理的范圍。關于粒子的整體質量,對比4種粒化算法的取值情況可知,MMIG-IT2FRCM 粒化算法在Lenses 和Iris 數據集下均取得了最佳值,在Wine 和Fertility 數據集下與其他3 種粒化算法的取值情況相近。 表5 UCI 數據集下4 種粒化算法的粒化指標Table 5 Granulation indicators of four granulation algorithms on UCI datasets 綜合4 個數據集類簇的交叉情況(Lenses 考慮反映粒子本質的核心指標,在類簇規模一致、數據分布均勻且邊界區域輕微交叉的Iris 數據集與類簇規模差別大、類簇重疊嚴重的Fertility 數據集下做進一步對比,4 種粒化算法的實驗結果如圖6 所示。可以看出,本文提出的MMIG_IT2FRCM 粒化算法相較其他粒化方法,在反映生成粒子性質與質量的核心指標上均取得理想表現,對類簇規模不均衡且邊界區域交叉重疊的數據集具有更強的適用性。 綜合2 組人工數據集和4 組UCI 標準數據集的實驗結果可知,本文提出的MMIG-IT2FRCM 粒化算法最終劃分形成的可信信息粒子具有更清晰的粒子語義,并最大化滿足粒度層次上實驗證據合理的成粒原理。 針對數據分布不均衡且多類簇交叉數據集的信息粒化問題,本文提出一種結合區間二型FRCM 與混合度量的兩階段信息粒化算法。基于快速收斂的IT2FRCM 聚類算法為粒化提供基本信息粒,同時考慮密度和區間的共同作用,改進粒子獨特性描述函數。在多組人工數據集和UCI 標準數據集下的實驗結果表明,本文算法在粒子兩大特性的多個指標上均取得了較為理想的結果,所得信息粒結構緊湊并具有代表性。針對不同分布且不同規模大小的數據集,下一步將自適應調整信息粒的粒度大小以實現不同層次的信息粒化,同時提高算法的適應性。
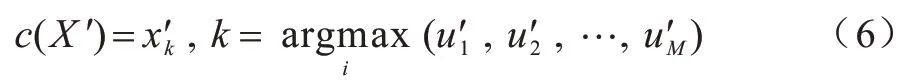
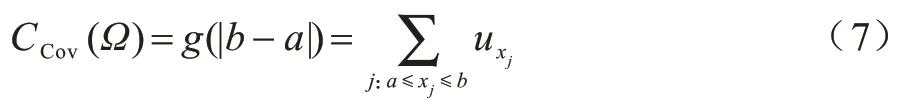
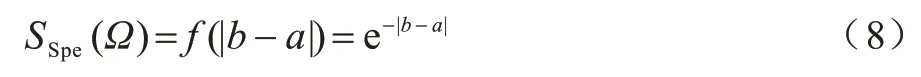
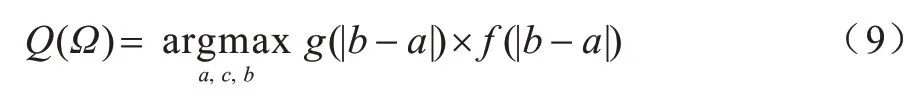
2 基于IT2FCM 與混合度量的粒化算法
2.1 考慮類簇不均衡性的IT2FCM 算法
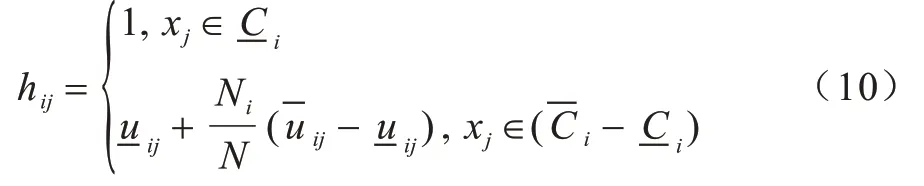
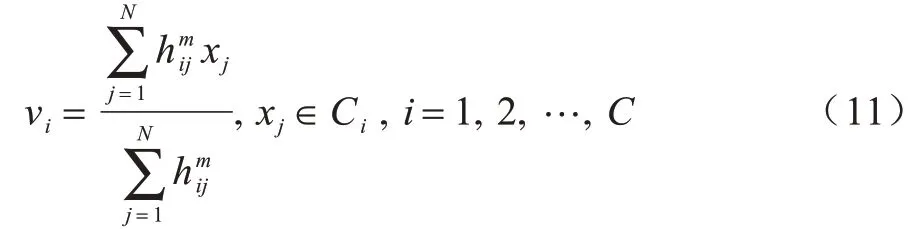
2.2 粒子特性描述問題

2.3 粒化算法
2.4 算法時間復雜度分析
3 實驗與結果分析
3.1 信息粒化兩階段數據初始化
3.2 人工數據集實驗結果分析

3.3 UCI 數據集實驗結果分析
4 結束語

