基于代理重加密的電子病歷數據共享方案

牛淑芬，劉文科，陳俐霞，杜小妮

（1.西北師范大學 計算機科學與工程學院，蘭州 730070；2.西北師范大學 數學與統計學院，蘭州 730070）

0 概述

電子病歷（Electronic Medical Record，EMR）是保存在計算機中的患者醫療記錄，其有助于醫生對患者進行正確診斷并制定合理的治療方案［1］。電子病歷信息不是靜態孤立的，而是動態和相互關聯的。相較傳統的紙質病歷，電子病歷具有更強的動態性與關聯性，新補充信息會與原有全部信息建立必要的聯系，電子病歷結構也不斷保持更新。近年來，隨著云計算技術不斷發展，電子病歷得到更廣泛的應用并趨于完善，越來越多的醫療機構與患者使用電子病歷，并將數據上傳到云端保存以方便使用。基于云的存儲系統比傳統存儲系統具有更多優勢，可使患者更快捷地存儲和維護數據，享受云計算帶來的高品質數據存儲服務。值得注意的是，由于云服務器可能被惡意破壞，云計算會造成患者隱私信息泄露等問題。

為確保患者隱私信息的安全性和保密性，電子病歷在上傳云端之前應進行加密。面對數量龐大的電子病歷，如何準確搜索加密數據成為難題。有研究人員提出下載所有加密數據，在解密密文后再進行檢索。該方法計算開銷較大且需要大存儲量設備，對于大型數據庫而言，其計算效率較低。近年來興起一種新型可搜索加密技術，其在完成密文檢索的同時可有效保證數據的隱私性。文獻［2］提出一種代理重加密方案對外包數據進行訪問控制，實現了云端密文數據共享。當數據擁有者Alice 與Bob進行數據共享時，Alice 用自身解密密鑰和Bob 的加密密鑰生成重加密密鑰并發送給云服務器，云服務器用重加密密鑰對密文進行重加密并保存在云端，此時Bob 可下載密文，并用自身私鑰進行解密得到原始明文，從而實現數據共享［3］。

為滿足數據用戶訪問患者電子病歷的需求，本文提出一種基于代理重加密的電子病歷數據共享方案。利用可搜索加密技術進行關鍵字搜索，通過代理重加密技術實現數據用戶對患者電子病歷的數據共享，并分別從關鍵字隱私和消息隱私兩方面證明數據用戶使用數據的安全性。

1 相關工作

為實現對密文的直接搜索，文獻［4］提出基于流密碼的對稱搜索加密方案。但基于對稱密鑰的可搜索加密方案的密鑰分發困難，從而造成其應用場景受限。為解決該問題，文獻［5］提出一種帶關鍵字的公鑰可搜索加密方案，并證明其在隨機預言機模型下具有安全性，但其密鑰傳輸需要安全通道。文獻［6］提出不需要安全通道的SCF-PEKS 模型，解決了文獻［5］中因使用安全通道造成原始可搜索加密方案效率低下的問題。文獻［7］提出基于模糊關鍵字搜索的公鑰加密概念。服務器對所有密文進行模糊關鍵字搜索后，返回結果給接收方，接收方對結果執行更精確的關鍵字搜索。可搜索加密通過給定關鍵字提供查詢加密數據的能力，將其應用于電子病歷中可保護患者的身份信息、通信信息和既往病史等隱私信息。文獻［8］提出一種高效、安全的細粒度訪問控制方案，可授權用戶訪問云存儲系統中的電子病歷。文獻［9］設計了一種云計算中基于屬性的可搜索加密電子病歷系統，使多用戶環境下密鑰管理難度降低，并實現了數據擁有者對電子病歷的細粒度訪問控制。文獻［10］提出用于移動醫療系統的無證書可搜索公鑰加密方案，采用無證書公鑰密碼體制解決了密鑰托管問題。用戶可將關鍵字及明文進行加密，并將密文上傳到云服務器。文獻［11］提出一種基于層次比較的加密方案，在基于云的電子病歷系統中利用代理重加密技術實現了動態訪問控制，并設計出動態策略更新方案。用戶在檢索數據時首先提交關鍵字限門，云服務器在搜索關鍵字后返回密文給用戶。然而由于只有患者知道密文解密密鑰，因此在患者將電子病歷用自身公鑰加密并將密文上傳到云服務器，同時授權數據用戶查看電子病歷時，數據用戶不知患者的私鑰，此時共享數據成為難題［12］。

為解決上述問題，文獻［13］提出密碼學原語帶關鍵字搜索的代理重加密（Proxy Re-Encryption with Keyword Search，PRES）的概念，并設計了雙向PRES 方案，在隨機預言機模型中驗證其具有安全性。文獻［14］提出指定檢驗者的具有關鍵字搜索性質的代理重加密的概念和安全模型，在標準模型下驗證其具有安全性。文獻［15］提出一種帶關鍵字搜索的限制性代理重加密的模型，在改進雙線性Diffie-Hellman（modified Bilinear Diffie-Hellman，mBDH）假設和隨機預言機模型的q 決策雙線性Diffie-Hellman 逆轉（q-Decisional Bilinear Diffie-Hellman Inversion，q-DBDHI）假設下證明其具有安全性。

針對目前只有醫生和患者中的一方才能對加密的電子病歷進行解密的現狀，本文以安全存儲、共享電子病歷數據為目標，利用可搜索加密和代理重加密技術提出一種基于代理重加密的電子病歷數據共享方案。醫生將患者的電子病歷加密后上傳到云服務器，患者利用可搜索加密技術對電子病歷進行搜索與解密。云服務器對上傳的電子病歷密文進行代理重加密后，經患者授權的數據用戶也可解密電子病歷。

2 理論基礎

2.1 雙線性對

令G1和G2是2 個階為素數q的循環乘法群，其中g為G1的一個生成元，定義一個雙線性映射e：G1×G1→G2滿足如下性質：

1）雙線性：對于任意a,b?，e(ga,gb)=e(g,g)ab成立。

2）非退化性：存在e(g,g)≠1。e(u,v)。

3）可計算性：對任意u,v?G1，存在有效算法計算

2.2 相關困難性假設

本文提出相關困難性假設如下：

1）mBDH 問 題［16］：對于任 意α,β,γ?，給 定g,gα,gβ,gγ?G1，mBDH 問題即計算

2）mBDH 假設［16］：任何概率多項式時間（PPT）算法均不能以不可忽視的優勢解決mBDH 問題。

3）q-DBDHI 問 題［17］：對于任 意x?，給定?G1，T?G2，q-DBDHI 問題即判斷是否成立。

4）q-DBDHI 假設［17］：任何PPT 算法均不能以不可忽視的優勢解決q-DBDHI 問題。

3 系統模型

本文提出的電子病歷系統模型結構如圖1 所示，指定電子病歷為m，其對應的關鍵字為w。該系統包含患者、醫生、數據用戶、醫院系統和云服務器5 個實體。

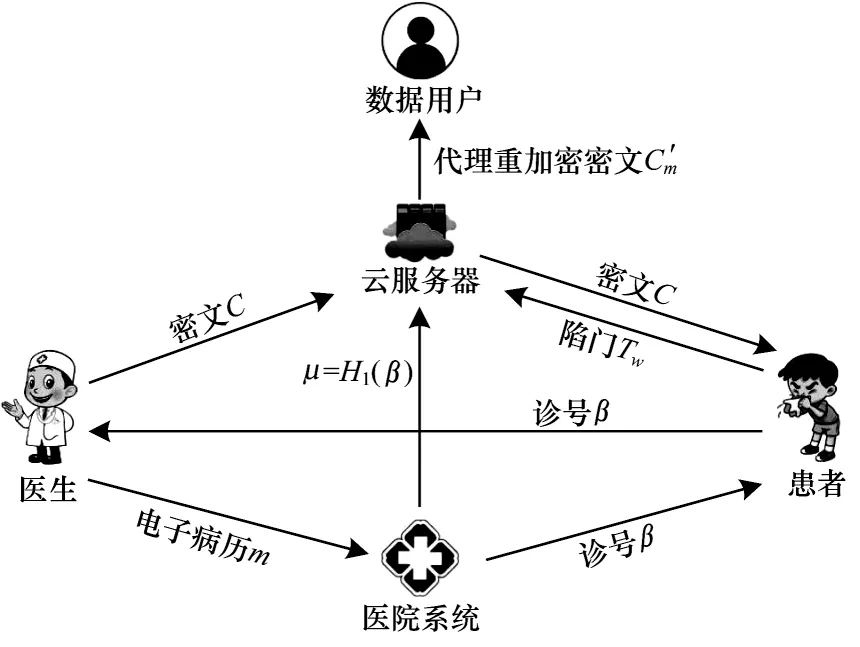
圖1 電子病歷系統模型結構Fig.1 Structure of electronic medical record system model

5 個實體具體說明如下：

1）患者。患者前往醫院就診時，醫院為其生成診號β，患者就診時將診號交給醫生。患者想要查看病歷時，可通過生成搜索陷門Tw獲取電子病歷密文C。

2）醫生。醫生為患者提供醫療服務。在患者診斷結束后，醫生將診斷結果記錄在電子病歷m中，同時生成關鍵字索引w，并將電子病歷m存入醫院系統。然后醫生使用患者的公鑰對m和w進行加密后將密文Cm和Cw上傳至云服務器進行存儲。

3）數據用戶。本文數據用戶指需要使用某患者電子病歷的用戶。例如，當患者病情復雜時，需要來自不同醫院的多位專家（數據用戶）進行會診，此時只需上傳患者的私鑰，云服務器使用生成的代理重加密密鑰rkP→R對密文C重加密生成密文。經患者授權后，云服務器返回密文給數據用戶，數據用戶可使用自己的私鑰進行解密。

4）醫院系統。醫院系統負責為患者生成診號β，并計算β的哈希值μ=H1(β)發送至云服務器。同時，醫院系統也負責存儲由醫生發送的電子病歷m。

5）云服務器。云服務器具有電子病歷存儲與搜索功能。云服務器先存儲由醫院系統所發送患者診號的哈希值μ，并在醫生上傳患者電子病歷m前對患者身份進行驗證，驗證通過后，云服務器接收并存儲患者的電子病歷密文C，并將其與患者診號的哈希值μ綁定。云服務器在收到患者的搜索陷門Tw后，返回電子病歷密文C給患者。數據用戶想獲取某患者電子病歷時，可請求該患者和云服務器進行交互，云服務器生成代理重加密密鑰后對電子病歷密文C進行重加密，生成電子病歷重加密密文Cm′ 并發送給數據用戶。

4 方案的形式化定義和安全模型

4.1 方案的形式化定義

帶關鍵字搜索的代理重加密方案由以下9 個概率多項式算法組成：

1）公共參數生成算法Setup(1k)。輸入安全參數1k，初始化算法并輸出公共參數PP。

2）密鑰生成算法KeyGen(PP)。輸入公共參數PP，密鑰生成算法輸出公鑰pk 和私鑰sk。

3）加密算法Enc(PP,pkP,w,m)。輸入公鑰pkP、關鍵字w和消息m，加密算法為醫生D 輸出原始密文C。

4）陷門生成算法Trapdoor(PP,w′,skP)。給定患者P 的私鑰skP和關鍵字w′，輸出限門

5）測試算法Test(PP,C,Tw′)。給定密文C和限門，當w′=w時，輸出1；否則輸出0。

6）患者解密算法Dec1(PP,skP,C)。給定患者P的私鑰skP和密文C，輸出消息m?M或錯誤符號⊥。

7）重加密密鑰生成算法Re KeyGen(PP,skP,skR)。給定患者P 的私鑰skP和數據用戶R 的私鑰skR，輸出重加密密鑰rkP→R。該過程由患者P、數據用戶R 和云服務器共同執行。

8）重加密算法ReEnc(PP,skP→R,C)。給定患者P到數據用戶R 的重加密密鑰rkP→R和原始密文C，將密文C轉換為數據用戶R 的密文。

9）數據用戶解密算法Dec2(PP,skR,Cm′)。給定數據用戶R 的私鑰skR和密文Cm′，輸出消息m?M或錯誤符號⊥。

4.2 安全模型

本文中安全性包括關鍵字隱私和消息隱私。

本文采用文獻［18］中的假設來定義關鍵字隱私，即靜態損壞。在該安全定義中，敵手必須在計算開始前確定損壞的云服務器，不允許出現自適應選擇損壞服務器和未損壞服務器。

游戲1（關鍵字隱私）在本文安全定義下，敵手可獲得除了兩個指定關鍵字相關的陷門之外所有陷門，但其不能判斷哪個關鍵字對應于給定的密文，從而保證只有擁有陷門的人才能進行測試。在后續選擇關鍵字明文攻擊下的不可區分性（Indistinguishability under Chosen-Plaintext Attack for Keyword，IND-CPA-K）游戲（游戲1）中，若無多項式有界敵手A 對挑戰者具有不可忽略的優勢，則稱本文方案具有關鍵字隱私。

1）詢問階段1。敵手A 進行如下詢問：

（1）未損壞密鑰詢問Opk。從KeyGen(PP)算法獲取一個新的密鑰對(pk,sk)，返回pk 給敵手。設Lu為誠實用戶的集合。

（2）損壞密鑰詢問Osk。從KeyGen(PP)算法獲取一個新的密鑰對(pk,sk)，返回(pk,sk)給敵手。設Lc為不誠實用戶的集合。

（3）陷門生成詢問Otg。敵手A 輸入(pk,w)，其中pk 來自Opk或者Osk，w?{0,1}*是密鑰空間的任意關鍵字，返回陷門Tw=Trapdoor(sk,w)，其中sk 是對應pk 的私鑰。

（4）重加密密鑰詢問Ork。敵手輸入(pkP,pkD)，其中pkP和pkD來自Opk或者Osk，返回重加密密鑰rkP→D=ReKeyGen(skP,skD)，其中skP和skD分別為pkP和pkD對應的私鑰。本文中要求pkP和pkD都損壞或者都未損壞，因此，不允許在損壞的密鑰和未損壞的密鑰之間生成重加密密鑰。

2）挑戰。階段1 完成后，敵手向挑戰者發送來自關鍵字空間相同長度的w0和w1，來自消息空間的m和公鑰pkD，其中pkD想要被挑戰。唯一的限制是敵手不能提前詢問陷門Tw0和Tw1，且pkD只能來自Lu。挑戰者選隨機數b?{0,1}，計算挑戰密文Cb′=ReEnc(PP,ReKeyGen(skP,skD),Enc(pkP,wb,m))并并發送給敵手。

3）詢問階段2。該過程與詢問階段1 相同，但不能詢問挑戰密文，具體如下：

（1）未損壞密鑰詢問Opk。該過程與詢問階段1相同。

（2）損壞密鑰詢問Osk。該過程與詢問階段1相同。

（3）陷門生成詢問Otg。敵手可繼續對任意關鍵字w執行陷門生成詢問，其中w≠w0且w≠w1。

4）猜測。最終敵手A輸出猜測b'?{0,1}，若b'=b，則敵手贏得游戲。

本文定義游戲的優勢為：

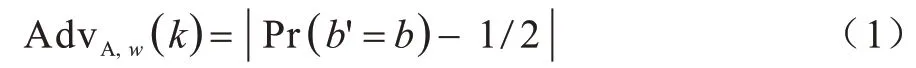
對于任何多項式時間敵手A，如果AdvA,w(k)是可忽略的，則稱電子病歷下基于代理重加密的數據共享方案在抵抗選擇關鍵字明文攻擊下是語義安全的。

游戲2（消息隱私）在本文安全定義下，敵手可以獲得所有陷門，但其不能判斷哪個消息對應于給定的密文，從而保證只有擁有私鑰的人才能對消息進行解密。在后續選擇消息明文攻擊下的不可區分性（Indistinguishability under Chosen-Plaintext Attack for Message，IND-CPA-M）游戲（游戲2）中，若無多項式有界對手A 對挑戰者具有不可忽略的優勢，則稱本文方案具有消息隱私。

1）詢問階段1。該過程與關鍵字隱私的安全模型相同。

2）挑戰。階段1完成后，敵手向挑戰者發送來自消息空間相同長度的m0和m1，以及來自關鍵字空間的w和公鑰pkD，其中pkD想要被挑戰。唯一的限制是pkD只能來自Lu。挑戰者選擇隨機數b?{0,1}，計算挑戰密文Cb′=Re Enc(PP,ReKeyGen(skP,skD),Enc(pkP,w,mb)并發送給敵手。

3）詢問階段2。該過程與詢問階段1 相同，但是不能詢問挑戰密文。

（1）未損壞密鑰詢問Opk。該過程與詢問階段1相同。

（2）損壞密鑰詢問Osk。該過程與詢問階段1相同。

（3）陷門生成詢問Otg。敵手可繼續對任意關鍵字w進行陷門詢問。

（4）重加密密鑰詢問Ork。該過程與詢問階段1相同。

4）猜測。最終敵手A輸出猜測b'?{0,1}，若b'=b，則敵手贏得游戲。

本文定義游戲的優勢為：

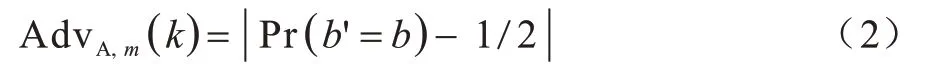
對于任何多項式時間敵手A，如果AdvA,w(k)是可忽略的，則稱電子病歷下基于代理重加密的數據共享方案在抵抗選擇消息明文攻擊下是語義安全的。

5 具體方案

本文定義患者為P，醫生為D，數據用戶為R。本文方案分為算法初始化、數據處理、數據搜索和數據共享4 個階段。為讓除患者以外的數據用戶共享電子病歷數據，本方案在階段4 中分別給出患者解密電子病歷和數據用戶解密電子病歷兩種情況。

1）階段1：算法初始化

在該階段，系統運行參數生成算法生成公共參數PP，系統運行密鑰生成算法生成醫生密鑰、患者的密鑰和數據用戶密鑰。當患者在醫院就診時，醫院隨機選擇β?{0,1}*，將β安全地發送給患者，并為該患者指定一名醫生［19］，計算μ=H1(β)發送到云服務器。

（1）Setup(1k)。系統輸入安全參數1k，輸出雙線性對e：G1×G1→G2，其中G1和G2是階數為素數q的乘法循環群，然后選擇隨機生成元g?G1，計算Z=e(g,g)。定 義4 個哈希函數：H0：{0,1}*→G1，H1：{0,1}*→G1,H2：G2→{0,1}lbq,H3：G2→{0,1}*。設置公共參數PP=(g,Z,e,q,G1,G2,H0,H1,H2,H3)。

（2）KeyGen(PP)。患者P 隨機選擇p?作為其私鑰skP，計算公鑰pkP=gp。醫生D 隨機選擇d?作為其私鑰，計算公鑰pkD=gd。數據用戶R隨機選擇r?作為其私鑰，計算公鑰pkR=gr。

2）階段2：數據加密

患者在就診時向醫生出示β，作為醫生為其生成電子病歷的授權。醫生使用β為患者生成電子病歷并上傳到云服務器，具體步驟為：醫生為患者診斷后生成電子病歷m和關鍵字w，上傳電子病歷m至醫院系統，然后運行加密算法對數據和關鍵字進行加密，生成電子病歷m的密文Cm和關鍵字w的密文Cw發送給服務器。

3）階段3：數據搜索

為搜索到加密后電子病歷的密文，患者需采用陷門生成算法計算關鍵字w′的搜索陷門Tw′并發送到云服務器。云服務器接收到搜索陷門后，調用測試算法檢查搜索陷門中w′對應的密文。若密文對應的w與搜索陷門中的w′相等，則云服務器發送電子病歷密文C給患者。

若w′=w，則等式成立，測試通過。

4）階段4：數據共享

患者在收到電子病歷密文C后，運行解密算法恢復得到子病歷m。

數據用戶若想獲取某患者的電子病歷，需請求患者和云服務器與其進行交互，生成代理重加密密鑰rkP→R。

6 安全性證明

由于患者使用數據時與數據用戶使用數據類似，因此本文僅證明數據用戶使用數據時的安全性。

6.1 關鍵字隱私

定理1假設mBDH 問題是困難的，那么本文方案為語義安全的，可抵抗隨機預言機模型中關鍵字的選擇明文攻擊。

證明5假設存在敵手A 以優勢ε(k)攻破本文方案中的關鍵字隱私，則可構造算法B 解決mBDH問題。其中，ε(k)是安全參數k的一個可忽略函數。

2）挑戰。當詢問階段結束時，A 生成一對關鍵字w0和w1，消息m和希望挑戰的公鑰pki，B 生成挑戰密文如下：

（1）若公鑰pki屬于LC，則B 退出。

（2）B 進行兩 次H1詢問獲 取h0,h1?G1使H1(w0)=h0和H1(w1)=h1。若c0=1 和c1=1 都成立，則B 報告失敗。

（3）c0和c1中至少有一個為0，B 隨機選擇b?{0,1}使cb=0。

根據該定義，Cb′ 為所需關鍵字wb的有效挑戰密文。

3）詢問階段2。該過程與詢問階段1 相同，但是不能詢問挑戰密文。

（1）未損壞密鑰詢問Opk。該過程與詢問階段1相同。

（2）損壞密鑰詢問Osk。該過程與詢問階段1相同。

（3）陷門生成詢問Otg。敵手A 可繼續對關鍵字wi進行陷門詢問，此處限制wi≠w0且wi≠w1。B 的回應與詢問階段1 中相同。

（4）重加密密鑰詢問Ork。該過程與詢問階段1相同。

4）猜測。A 輸出猜測b′?{0,1}，猜測Cb′ 是對w0的加密還是對w1的加密。B 從H2表中選擇隨機對(t′,V)，輸出作為對的猜測，其中，ab在H1表中，用于挑戰階段。

6.2 消息隱私

引理1若無多項式時間算法在求解簡化的q-DBDHI 問題上具有不可忽略的優勢，則簡化的q-DBDHI 問題是難以解決的。

定理2假設q-DBDHI 問題是困難的，則本文方案是語義安全的，可抵抗隨機預言機模型中關鍵字的選擇明文攻擊。

這部分證明的部分過程與定理1 中相同，以下只進行簡單證明，并說明q-DBDHI 假設是如何應用于本文方案。

證明6對于k?，令gc為gbk，則消息m在公鑰gb下的加密密文為：

若T=成 立，則C1'為消息m的正確密文；否則為其他消息m′≠m的密文。除非對手推翻q-DBDHI 假設，否則其不會破壞本文方案的語義安全性。

7 效率分析

本節討論本文方案在加密階段、搜索階段和解密階段的運算時間，并比較已有的可搜索加密方案與本文方案在運算時間上的優劣。在Linux 操作系統下利用雙線性包實現算法，使用C 語言進行編程，在PC 機（惠普電腦，3.1 GHz CPU，4GB RAM）的虛擬機中運行。

7.1 理論分析

以下從理論角度分析本文方案與文獻［12］方案、文獻［20］方案在運算時間上的優劣。表1 為上述方案中基本運算執行時間的符號和時長。由于計算開銷中指數運算、配對運算和哈希運算時間較長，因此只考慮這3 方面的運算時間。

表1 基本運算的執行時間Table 1 Execution time of basic operations ms

利用表1 中數據得出加密階段、搜索階段和解密階段的運算時間，結果如表2 所示。由表2 可以看出：在加密階段，各方案運算時間由大到小依次為文獻［12］方案、本文方案和文獻［20］方案；在搜索階段，各方案運算時間由大到小依次為文獻［12］方案、文獻［20］方案和本文方案；在解密階段，各方案運算時間由大到小依次為文獻［12］方案、文獻［20］方案和本文方案。

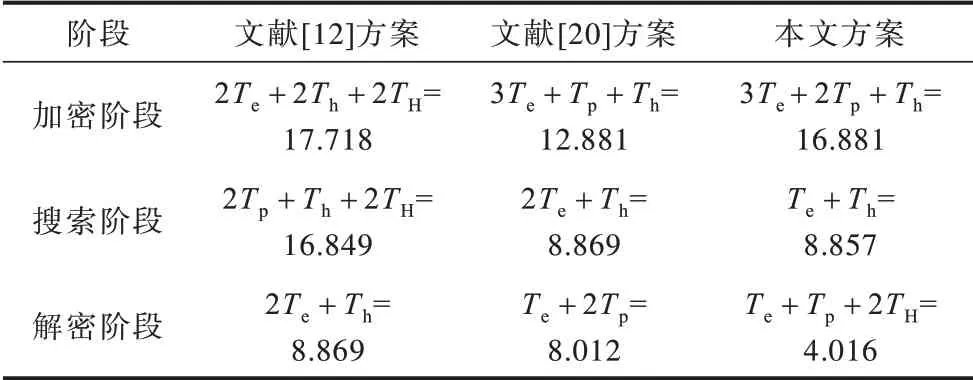
表2 3 種方案不同階段的運算時間Table 2 Operation time of different stages of three schemes ms

7.2 數值模擬

本節數值實驗通過改變關鍵字個數，對比本文方案與文獻［20］方案在加密階段和搜索階段的算法的時間開銷。關鍵字個數分別取10、20、30、40、50、60、70、80、90 和100，取算法運行50 次所得結果的平均值作為最終實驗結果。

本文方案和文獻［20］方案在加密階段的時間開銷如圖2 所示。可以看出，兩種方案在加密階段的時間均隨關鍵字個數的增加而增長，但本文方案的時間增幅較緩，即關鍵字個數越多，本文方案在加密階段的運算時間較文獻［20］方案的優勢更明顯。例如：當關鍵字個數為10 時，兩種方案在加密階段的時間差距可忽略不計；當關鍵字個數為100 時，文獻［20］方案在加密階段的運算時間高于本文方案600 ms。因此，對于云服務器中大批量數據而言，本文方案更能滿足實際需求。

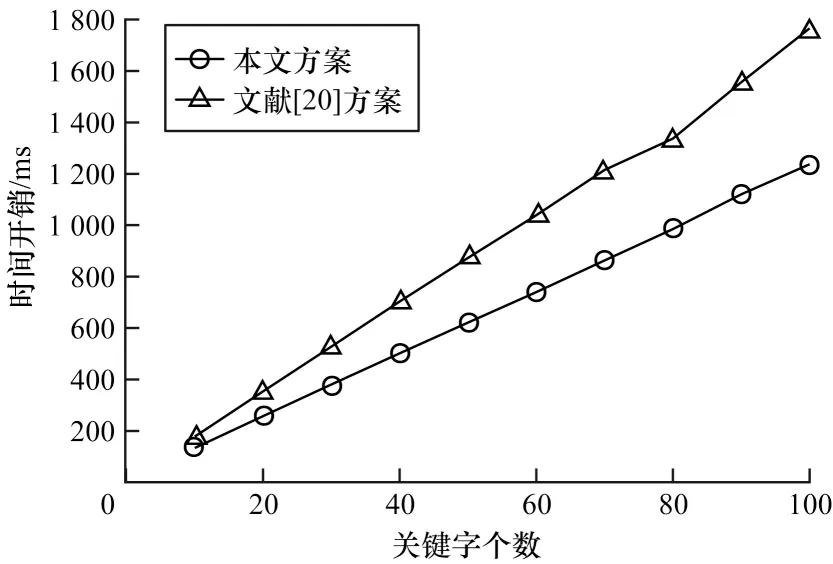
圖2 2 種方案加密階段的時間開銷Fig.2 Time cost of encryption phase of two schemes

本文方案和文獻［20］方案在搜索階段的時間開銷如圖3 所示。可以看出，兩種方案在搜索階段的時間開銷隨關鍵字數量的增加呈線性增長，但本文方案的時間開銷增幅較緩，其在實際應用中云服務器的響應時間更短，用戶搜索更迅速。

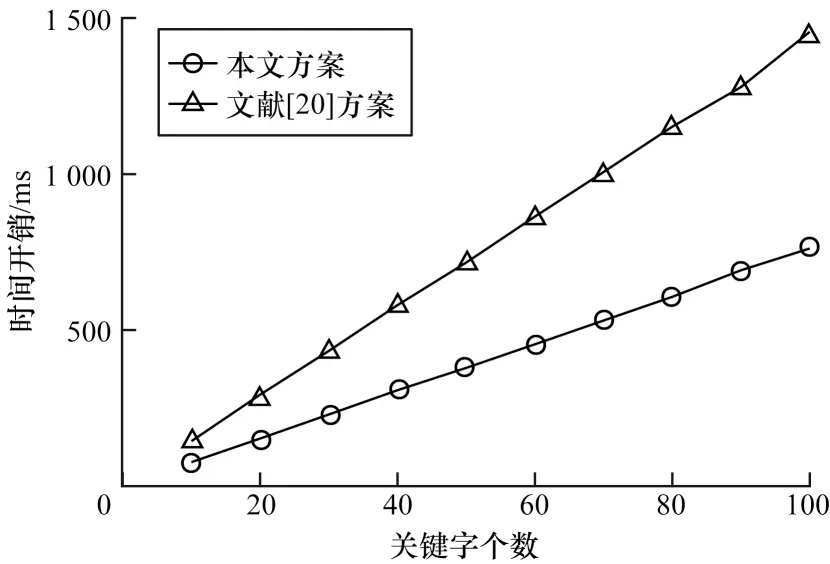
圖3 2 種方案搜索階段的時間開銷Fig.3 Time cost of search phase of two schemes

8 結束語

本文提出一種基于代理重加密的電子病歷數據共享方案。在保證隱私安全的基礎上，患者獲取以其私鑰解密的加密電子病歷，數據用戶經患者授權能查閱其電子病歷。基于隨機預言機模型的實驗結果表明，該方案有效實現了關鍵字隱私安全和消息隱私安全，可滿足實際應用需求。由于本文方案僅支持單關鍵字搜索，搜索效率較低，后續將拓展為支持連接關鍵字搜索，以提高關鍵字搜索效率。