服務企業排隊系統的顧客等候補償及等候時間保證策略研究

■ 龔其國 易春曉

中國科學院大學經濟與管理學院 北京 100190

0 引言

2013年以來，中國服務業實現了平穩快速的發展，服務業超過工業成為中國經濟增長的第一動力。在市場規模不斷擴大的情況下，服務行業的不可儲存性、生產消費的同步性導致了供給與需求的不匹配，進而導致了排隊現象的產生。

因此，越來越多的文獻開始研究服務行業的排隊問題。最初，研究者將顧客視為完全理性，研究了顧客加入隊列的問題。部分學者認為顧客是否加入隊列取決于隊列長度，高于某個閾值顧客就不會加入，反之，低于這個值顧客才會加入隊列[1]。還有一部分研究者研究了不知情消費者(Uninformed Consumer)對知情消費者(Informed Consumer)的排隊跟隨的問題[2-6]。后來有許多研究者站在企業的角度研究問題，研究了企業在面對顧客排隊行為時的價格決策和服務策略[7-9]。同時也有排隊論學者主要聚焦與如何最優化服務布局[10]以及動態調整服務率的雙閾值策略[11]。

長時間而枯燥的排隊可能會讓顧客在到達隊列時選擇不加入。對于顧客來說，在期待更好的服務的同時往往會期待更短的排隊等候時間。如何降低顧客在排隊過程中的等待時間，是整個服務企業亟需解決的問題。因此劉健等[12]研究分析了服務機制和定價策略對客觀等待時間的影響，而李武強等[13]研究分析了服務速率對客觀等待時間的影響。然而由于服務企業的空間限制或者成本問題，這些方案只能在一定程度上減少客觀等待時間。

而顧客在等待過程中的體驗也直接影響其對等待時間的感知和判斷，因此企業在制定減少顧客排隊時間的策略時，還必須考慮顧客的排隊體驗。為了緩解排隊顧客的焦慮情緒，企業常常為排隊中的顧客提供一些補償服務，以減少顧客等待帶來的負效用，例如海底撈往往會在大廳里專門留出一個區域來當作顧客候餐區，同時在候餐區提供美甲、撲克牌等活動。還有一些企業會在等待環境中設置專門的燈光環境、裝修風格和電視機、游戲機等娛樂設施來減少顧客的感知等待時間[14-15]。目前，越來越多的研究者開始將目光轉向減少消費者感知等待時間的變化。劉健等[16-17]研究了企業如何通過定價、折扣等調整顧客的期望等待時間。Liang[18]直接提出改善排隊環境可以減少顧客感知等待時間。Yuan[19]等研究了具備合作競爭能力的服務企業為等候的顧客提供的最優娛樂設施(Entertainment Options)和服務價格決策。孔瑞曉等[20]研究了考慮等待補償成本下的雙寡頭競爭策略。還有研究者考慮了智能點餐系統及智能機器人的應用對消費者感知等待時間的影響[21-24]。

另一方面，基于等待時間的競爭已經被越來越多的企業所接受，對于企業來說，面對排隊等候的顧客，除了選擇提供等候補償之外，還可以選擇給顧客一定的預期等候時間保證，以減少顧客的等候焦慮。例如在游樂園，工作人員會標注在某位置排隊時預計要等待多久，有些需要排隊等待的餐廳也會告知顧客的預期等待時間。許多服務公司將向等待中的消費者承諾預期等待時間作為一種營銷手段，在時間敏感的市場中吸引客戶。最近有幾篇論文研究了類似的問題。So[25]研究了服務企業服務交付時間(Delivery Time Guarantees)和價格決策對利潤最大化的影響。Yu 等[26]研究了企業如何通過等待時間保證來控制顧客的選擇。

通過分析前人的研究發現，目前大多數文獻都集中在等候補償對感知等待時間的影響機制的研究上，幾乎沒有文獻聚焦于計算出企業的最優等候補償水平，更沒有文章同時關注最優的等待補償水平和等待時間保證，而等待補償水平和等待時間保證決策是每個服務企業在面對排隊問題時都要解決的問題。因此，不同于此前的研究，首先，本文旨在通過定量分析，探究服務企業在壟斷情形和雙寡頭壟斷情形下補償水平的最優決策。另一方面，探究了企業同時考慮等待補償水平和等待時間保證的最優決策。

本文借鑒了前人的研究成果，建立了以M/M/1 排隊系統為基礎的企業等候補償和預期等待時間決策模型。首先分析了企業在不承諾等候顧客預期等待時間的情形下顧客加入隊列的概率，然后以此計算企業最優的顧客等候補償水平決策，并考慮了雙寡頭競爭情形下企業的最優補償水平決策。然后分析了企業在向顧客承諾預期等待時間的情形下，企業最佳的最優的等待時間保證與補償水平。該模型下顧客為完全信息，因此在系統到達率不變的情況下，當價格、等候補償水平一定時，實際顧客加入率為確定值。

本研究模型得到了壟斷情形和雙寡頭情形下企業最優的等待補償水平的解析解以及企業同時考慮補償水平和等待時間保證時的最優解，并做了相應的敏感性分析。

1 不承諾預期等待時間：壟斷企業最優補償策略研究

1.1 研究問題

在排隊過程中，顧客在到達排隊系統后會綜合考慮接受服務的收益、價格、等候時間等因素，只有當期望效益大于零時才會加隊隊列。因而對于企業來說，制定合適的顧客等候補償策略，可以有效減少顧客的等待焦慮，提高顧客的期望效益，同時提高顧客的加入率。本節研究了關于壟斷企業最優補償水平的決策，并考慮了價格等因素對其決策的影響。

1.2 基本假設

假設1：企業的排隊系統為先到先得（FCFS），顧客具有理性決策能力，且是同質和風險中性的。顧客相繼到達系統的時間間隔從負指數分布，最大的系統到達率為λ，這一數值受市場影響，假設為外生。企業對每個顧客的服務時間服從參數為μ的負指數分布（λ＜μ）。

假設2：假設顧客接受服務后所得收益為R,顧客單位時間的等待成本為h，服務價格為P，其中(P＜R)。

假設3：企業為降低顧客在到達排隊系統后選擇離開（renege）的概率，會給參與排隊（join）的顧客一定的排隊補償，以縮短其感知等待時間。參考yuan等[19]的文章,假設α表示企業對正在等候的所有顧客的補償水平，企業達到該供給該補償水平所需要的成本表示為C(α),由于規模不經濟，補償成本函數為凸增的，成本函數為

假設4：顧客進入隊列后具有不完全信息，排隊系統中的價格、等候補償水平等可以通過已有的經驗來獲得，而在到達隊列時卻難以知悉隊列的具體長度，只能根據已有的經驗來估計期望等待時間。根據Ward Whitt等的假設[23]，可以假設當消費者對隊列長度不知情時，到達系統的顧客有q的概率進入隊列，因此隊列的實際加入率=qλ。排隊隊列中顧客的期望逗留時間為

1.3 壟斷情形下顧客排隊補償策略與定價模型

顧客的期望收益為[27]：

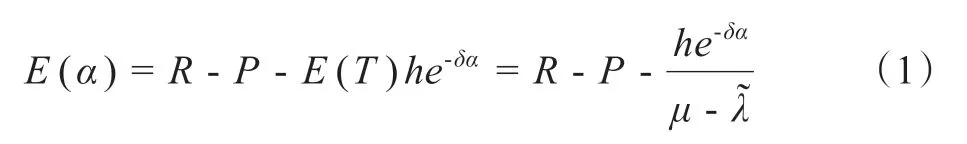
分情況討論顧客的均衡策略：

當(R-P)(μ-λ) ＜he-δα＜(R-P)μ時，一部分顧客選擇離開隊列，一部分顧客選擇加入隊列，顧客加入隊列的概率為：

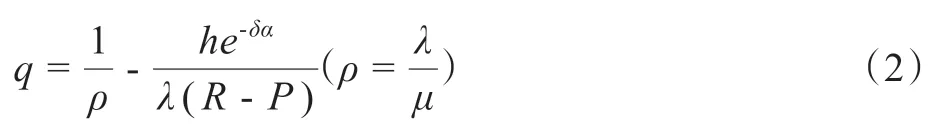
當he-δα≥(R-P)μ時，所有的顧客都離開隊列，此時q= 0。而當(R-P)(μ-λ) ≥he-δα時，所有的顧客都加入隊列，此時q= 1。

對于企業來說，利潤函數為：

命題1：對于企業來說，當補償成本一定時，存在一個唯一的補償水平α*，使得在顧客知曉隊列長度的情況下達到利潤最大化。

證明：對利潤函數求導可知

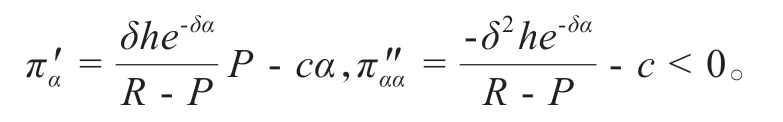
當he-δα=(R-P)μ時，π′α|he-δα=(R-P)μ=δμP-cα。

當he-δα=(R-P)(μ-λ) 時，π′α|he-δα=(R-P)(μ-λ)=δ(μ-λ)P-cα。

因此，存在最優的α*滿足：

推論1：當補償成本c和顧客等待成本h一定時，隨著產品價格P的增加，所需最優的補償水平α*增加。

對（6）求偏導得：

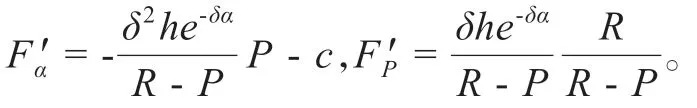
可以得到，α*隨著P單調遞增。

這是因為價格提高會降低顧客加入隊列的凈效用，因此需要給等候的顧客提供更多的補償以提高顧客加入隊列的概率。

那么令F′δ= 0,可得：將其代入F(α) = 0中可得也即是存在一個當δ＜δ* 時，F′δ＞0，當δ＞δ* 時，F′δ＜0。由于因此，當δ＜δ*時，最優的補償水平α*隨著補償有效性δ的增加而增加，當δ＞δ*時，最優的補償水平α*隨著補償有效性δ的增加而減少。

這是因為，當δ較小時，企業為了提高顧客加入隊列的概率而給顧客提供較高的補償水平是不劃算的，此時，企業將選擇較低的等候補償水平。隨著δ的增加，企業會提高其給顧客的補償水平。然而當δ足夠大時，給顧客提供的等候補償將會非常有效，因此不需要太高的補償水平。而當補償成本較大時，提供過高的補償水平顯然得不償失。

企業的利潤函數（3）對P求導，得：

由于而因此，當給定的補償水平α滿足時，

此時存在最優的P*，滿足0 使得企業的利潤最大化。 此時，P*∈[R-

當給定的補償水平α滿足時，，此時企業的利潤隨著價格的增加而減少，因此最優的價格為最低價格，即此時所有的顧客都會進入隊列。

推論3：當補償成本c和顧客等待成本h一定時，隨著企業提供給顧客的補償水平α的增加，最優的產品定價P*也在增加。

綜上可知，隨著企業提供給顧客的補償水平α的增加，最優的產品定價P*也在增加。這是因為，當企業提供更高的補償水平的時候，一方面增加了成本，企業需要提高價格以維持利潤，一方面增加了顧客的到達率，企業有動力提高價格以獲得更高的利潤。

推論4：對于企業來說，如果補償水平對企業變得更有效（δ增大），那么最優的產品定價P*也會增加。

所以如果補償水平對企業變得更有效（δ增大），那么最優的產品定價P*也會增加。這說明，隨著δ的增加，等候補償在減少顧客等待的負效用方面變得更加有效，反過來可以以更高的價格銷售服務。

2 不承諾等待時間：雙寡頭競爭市場的排隊系統顧客補償策略研究

2.1 問題提出

上一節假設了市場中只有一個企業的情況下企業對排隊顧客的補償和定價策略，在本節中，加入市場競爭因素，模擬了提供相同服務類型的公司之間的雙寡頭壟斷競爭，在本節的假設中，每個公司都提供自己的等候補償，專門針對自己的客戶。

2.2 假設

不失一般性的，假設兩個服務提供者是對稱的，兩個公司（企業i，企業j）提供的服務完全同質，面對相同的市場，即最大的系統到達率都為λ。因此可以假設企業的加入率都為=qi,jλ，由于存在市場競爭，因此市場價格為統一市場價格，并由企業i和企業j的需求量決定，即：P=P0-m(qiλ+qjλ)，m表示需求的價格彈性，P0表示最高價格。由于市場上具有統一的價格，因此在考慮顧客選擇的期望效用模型時，可以不必考慮產品價格，假設顧客接受服務所得到的收益為R1（R1＜R，表示扣除了價格之后的純收益），則顧客加入隊列i的期望效用為：

2.3 模型分析

根據顧客的期望效用模型，當R1(μ-λ) ＜he-δαi,j＜R1μ時，到達企業i（企業j）的一部分顧客選擇離開隊列，一部分顧客選擇加入隊列，顧客加入隊列i（隊列j）的概率為(其中)，當he-δαi,j≥(R1-P)μ時，所有的顧客都離開隊列i（隊列j），此時qi,j= 0。而當(R1-P)(μ-λ) ≥he-δαi,j時，所有的顧客都加入隊列，此時qi,j= 1。為了簡化研究，本節只研究第一種情況下兩企業的博弈問題。

對于企業i來說，收益函數為：

命題3：在雙寡頭競爭的情況下，當其他條件一定時，企業i，企業j存在一個最優的補償水平均衡αc，該補償均衡滿足：

證明：給定企業j對等候顧客的補償水平αj，企業i通過最優的補償水平αi來最大化其利潤，類似于市場上只存在一個企業的情況，最佳的補償水平αi滿足以下一階條件：

令：

此時，給定一個αj的值且因此，對于以一個固定值αj，存在一個唯一的αie(αj)使得Z(αi*(αj),αj)= 0。因為兩個企業是完全同質的，在均衡的情況下，兩個企業必須選擇相同的補償水平。定義最優的補償水平為αc，則，Z(αc,αc)= 0。

由此可得，兩個企業最優的補償水平αc滿足：

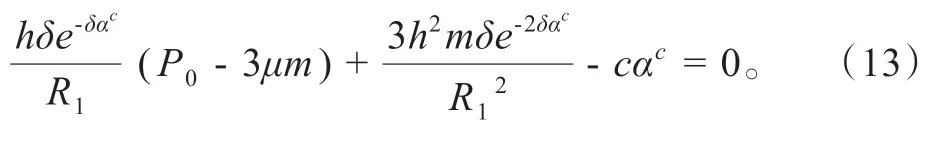
此時顧客加入隊列的概率為：

3 承諾預期等待時間，企業排隊系統等候補償及等待時間保證策略

3.1 問題提出

在當今競爭激烈的市場中，正如上文所述，價格往往是市場和消費者博弈的結果，單個商家不具備改變價格的能力，因此服務水平和等候時間的保證是服務企業成功的兩個重要因素。雖然等候時間保證是一個很有力的營銷武器，但是如果企業無法在保證的時間之內服務顧客，將會使企業的商譽和信譽受到很大打擊，反而適得其反。因此，建立一個分析模型來研究企業如何在市場中制定等候補償和等候時間保證是很有用的。本章試圖解決的基本研究問題是，在顧客對等候時間非常敏感的競爭市場中，企業如何選擇其等候補償水平和時間保證。

3.2 基本假設

假設1：由于本模型研究的是M/M/1 類型的隊列，為了方便研究，可以使用顧客在排隊系統中的逗留時間（等待時間加服務時間）來近似企業提出的等待時間保證。由于到達率和服務率都服從負指數分布，因此如果企業提供的時間保證必須滿足ε(95%)的顧客，則等待時間約束為[25]：

也即是(μ-)t=ln(1-ε)表示顧客的實際到達率。

假設2：假設顧客的相繼到達系統最大到達率都為λ，由于顧客在到達企業時被承諾了預期等待時間，因此顧客獲得了隊列的完全信息。那么，實際的顧客加入率(join)受到服務價格P、預期等待時間t和企業為等候顧客提供的補償量α的影響，當這些系數確定時，顧客的實際加入率也確定，本文根據Yuan等[19]的文獻對消費者的加入率的假設，將加入率設為：

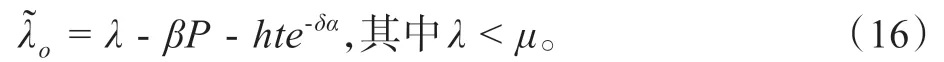
其中β表示消費者對價格的敏感性，h表示每單位時間的等待成本，即顧客對等待的厭惡程度，δ表示給顧客提供的補償水平α的有效程度。正如假設所表示的那樣，補償水平α減少了顧客等待的厭惡程度。

假設3：提供等候補償是有成本的，為了提供α的補償水平，成本為C(α)。跟上文一致，根據yuan 等的文章，補償成本可以假設為[19]：

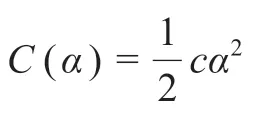
同時c為正常數，表示補償水平對成本的敏感系數。

假設4：企業的目標是考慮選擇最優的預期等待時間保證和最優的補償水平，由于企業的預期時間保證與其服務率有關，因此本節加入對企業服務成本的考慮。假設企業服務一個顧客的邊際成本為γ，目標函數為[19]：

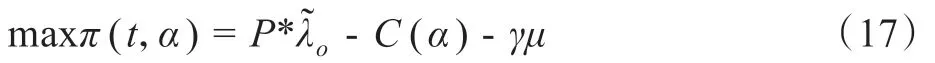
3.3 模型分析

由公式（17）可知最優的預期等待時間和等候區補償水平的目標函數為：

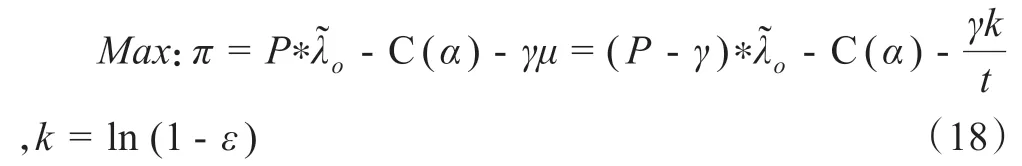
其中，P為外生。也可以化簡為：

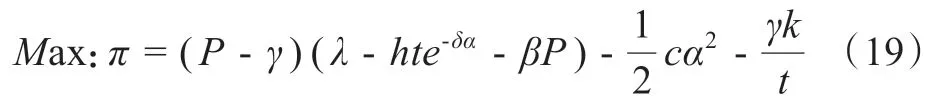
命題4：給定企業的定價，最優的補償水平αo滿足：(P-γ)htδe-δαo-cαo= 0

同時最優的預期等待時間保證to滿足：γ)*he-δα= 0

證明：

對公式（18）求導得：

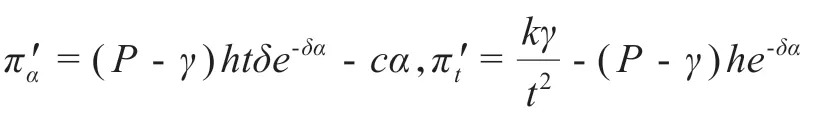
令二者為零可以的最優的補償水平αo和標準等待時間to，因為：

令，π″αα= -(P-γ)hδ2te-δα-c=A

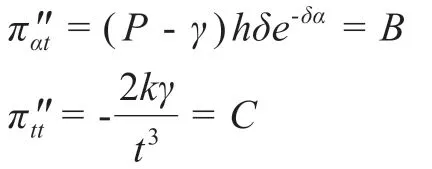
將π′t= 0代入可得：

因此αo與to是最優解。

推論5：最優預期等待時間to隨著補償有效性δ的增大而增大；存在一個δo，當δ＜δo時，最優的補償量αo隨著δ的增加而增加，反之，最優的補償量αo隨著δ的增加而減少。

證明：將π′t= 0帶入π′α= 0中得：

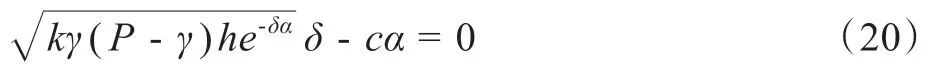
令：

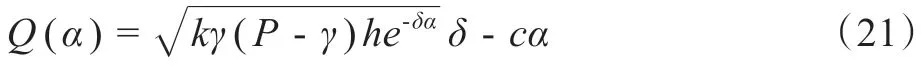
對其求偏導得：

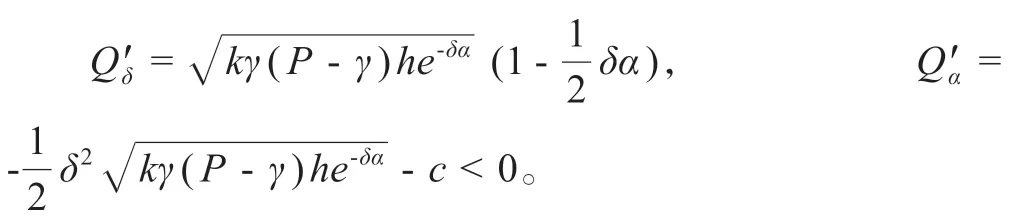
令Q′δ= 0 得：，將代入Q(α) = 0中得，顯然存在一個δo=當δ＜δo時，Q′δ＞0，當δ＞δo時，Q′δ＜0。

由π′t= 0得：

對其求導得：

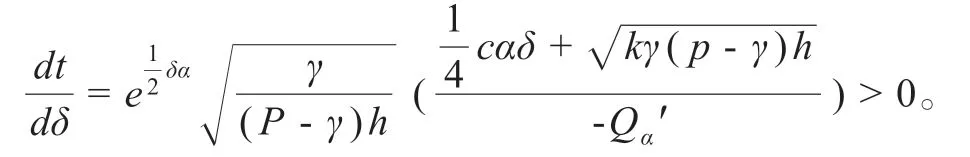
因此，預期等待時間to隨著補償有效性δ的增大而增大。這是因為當補償的有效性增大時，相同的補償水平下顧客的感知等待時間較低，企業可以適當的提高其等待時間保證。

推論6：隨著價格的升高，最優的補償提供量αo應當增加。但是最優的預期等待時間to應當減少。

證明：對公式（21）求偏導得：

這是因為，當價格升高時，企業要維持其利潤，必須增加其等待補償水平，并降低顧客的等待時間保證，以吸引更多的顧客。

4 研究結論

本文旨在研究企業面對排隊顧客時的最優等待補償水平和最優等待時間保證。因此，在理性顧客假設的基礎上，本文首先提出了壟斷企業面對M/M/1 排隊系統的顧客補償策略和定價策略，然后本文考慮了在雙寡頭競爭市場下企業面對排隊系統的補償策略模型。和以往的模型不同，在該模型中，顧客以一定的概率加入隊列，概率由顧客和企業雙方博弈決定，同時在雙寡頭壟斷的企業模型中考慮了企業的古諾博弈。在雙寡頭壟斷模型中，假設市場價格由市場對雙方的需求決定，每個企業都沒有單獨改變價格的動力。

在當今競爭激烈的市場中，許多服務公司都在向顧客提供等待的時間保證。本文在進一步的研究中考慮到了這一點，設計了一個分析等候補償和等候時間策略的模型。該模型考慮了市場和企業的幾個主要特征的本質，例如當顧客知曉了等待時間、價格以及等候補償水平時，實際到達率是定值。

本文的工作可以總結為以下4點：

（1）基于顧客存在感知等待時間的情形，構建了顧客的期望效用模型和企業的收益函數。

（2）基于顧客的期望效用模型和企業收益函數，提出了壟斷情形下企業存在最優的等待補償水平決策與價格決策。同時，分析了價格和等待補償水平的相互影響作用。

（3）考慮雙寡頭企業的古諾均衡博弈，雙寡頭壟斷下企業具有同質的產品和服務，得到了雙寡頭企業競爭時顧客加入隊列的概率和兩個企業最優的補償水平。

（4）當將企業的等待時間保證加入模型時，本研究得到了企業同時決策補償水平和等待時間保證下的最優解析解。并進行了相應的敏感性分析。

通過模型分析，本文的研究得到了如下成果：第一，企業在寡頭壟斷和雙寡頭競爭下的最優等候補償水平決策的解析解。第二，得到了企業同時考慮預期等待時間和等待補償水平時的解析解。第三，當企業的等候補償水平變得更有效時（即顧客對等候補償的敏感性），存在一個敏感性的閾值，高于這個閾值時，補償水平越有效，所需的補償水平越低，反之，補償水平越高。

本模型的研究結果有助于識別時間保證和等候補償競爭中的關鍵市場因素和重要的企業特征，并對企業在不通過市場環境下如何選擇競爭具有重要的啟示意義。

基于本研究，服務企業在面對排隊顧客時，可以考慮為顧客提供等候補償和等待時間保證服務，并針對不同的市場情形考慮不同的等候補償策略和等待時間保證策略。但是在考慮提供等候補償和等待時間保證時，應當充分考慮價格和顧客對等候補償的敏感性的影響。例如，當定價較高時，應當有較高的補償水平來“對沖”高價格帶來的負效用。當等候補償的有效性提高時，應當具體分析是否超過顧客敏感性的閾值之后在決策補償水平。

本文的研究還具有一定的局限性，例如本文討論了最基本的M/M/1 排隊模型，而真實的系統往往不止一個服務臺，也不具備無限的等候空間，甚至顧客也未必是完全理性和完全信息的。同時，在現實生活中，市場上可能具有兩個以上的服務供應商，同時服務供應商也未必是對稱的。另外，在實際生活中，企業可以調整其服務速率，顧客的到達率也會受到更多條件的影響，顧客在加入隊列后也會有中途離開（balk）的可能性，這些都需要進一步的研究。