考慮作業時間的區段站調車鉤數分配分析

于澤濤，辛禹辰

(1.山東高速軌道交通集團有限公司 濟南工程分公司，山東 濟南 250101；2. 煙臺職業學院 經濟管理系，山東 煙臺 264670)

0 引言

調車作業是鐵路運輸過程中必不可少的內部生產環節，其效能的發揮直接決定了鐵路運輸企業的效率和效益[1-2]。調車鉤數是衡量調車作業量的一種單位，通常用其多少來表示調車作業量的大小。在區段站調車人員作業時間確定的情況下，預估取送調車作業中產生的調車鉤數并生成合理的調車作業量分配方案，能夠充分調動員工積極性，進而提高生產效率。

調車鉤數的合理分配對于制訂有效的調車作業計劃有重要作用[3]。目前針對調車鉤數的相關研究較多，如高四維等[4]提出了在調車線數量和可變條件約束下，實現統計調車鉤數最優的“消逆法”理論；王雅琳等[5]提出了一種基于排序二叉樹的編組鉤計劃自動編制方法，得到列車編組調車鉤數最優數據。張博健等[6]將調移車輛數進行優化的思想融合到調車鉤數最優的目標中。上述研究從不同角度直接或間接解決了調車鉤數分配問題，但均未將作業時 間[7]考慮到調車鉤數分配分析中。實際生產中在區段站往往使用多臺調車機車處理調車作業，如果分配的調車鉤數不均衡，會引起作業時間分配不均，進而影響工作效率。因此，構建基于作業時間的區段站調車鉤數分配模型，以期為車站調度員合理制訂調車作業計劃提供有益的參考。

1 考慮作業時間的區段站調車鉤數分配模型

1.1 問題描述

區段站取送調車作業是指調機從到發線出發，往相關貨物線進行取、送、調移作業后，返回到發線的技術作業過程。按照實際作業內容的不同，具體的區段站貨物線調車作業有取車、送車、同時送取3種作業形式。區段站為了加速車輛周轉，會盡量利用本站卸空后的空車裝車，存在車輛從卸車作業點移動至相應的裝車作業點的調移需求[3]，因而在取車、送車和同時送取車過程中都有可能發生調移作業。

區段站往往由多臺調機完成取送調車作業，為了合理分配調車作業任務，車站調度員編制調車作業計劃時，需要考慮各調機對應的調車人員作業時間均衡問題，實質上就是取送調車作業過程中調車鉤數均衡分配問題。綜上，在考慮最長限定作業時間、發車數量、接車數量及到發線數量因素[8]的基礎上，確定每一項作業的標準作業時間，求得調機每日最多可以處理的調車鉤數目，可以為調車人員合理分配調車鉤數，從而實現調車作業計劃制訂的有效性。

為了便于問題求解，結合實際做以下假設：調車車列中不存在多種車輛混和編組的情況；多臺調機作業時，只能由一臺調機處理調移作業；不考慮車輛因技術問題或裝載超噸而產生的甩車作業。

1.2 模型建立

在區段站調車作業中，以調車鉤數最優為目標，構建考慮作業時間的區段站調車鉤數分配模型，具體表示為

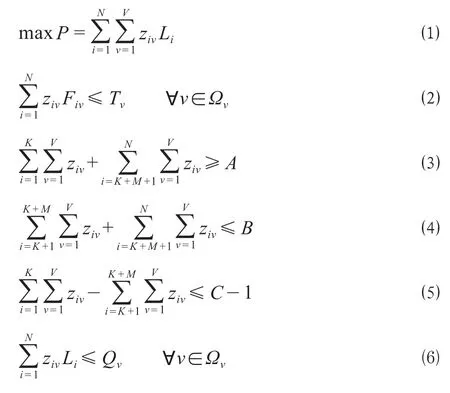
式中：P表示調車鉤數量，鉤；ziv表示調機v每日處理調車形式i的數量，且數量不小于0，種；Li為調車形式i包含的鉤數，鉤；N表示調車形式的總數，種；V表示調機的總量，輛；Fiv表示調機v處理調車形式i的標準作業時間，s；Tv表示每日調機的最長限定作業時間，s；Ωv表示調機v的集合，v= {1，2，…，V}；K表示只取不送車輛的調車形式數量，種；M表示只送不取車輛的調車形式數量，種；K + M +1表示同時送取車輛集合中第一種調車形式；A表示每日貨物線已裝載完成可以發出的車列數，列；B表示每日根據列車運行圖統計的到達車列數，列；C表示站內到發線的數量，條；Qv表示每日調機v可處理調車鉤數的最大能力，鉤。ΩD表示帶車輛調移的調車形式i的集合，ΩD= {W +1，…，K}∪{K + E +1，…，K + M}∪{K + M + R +1，…，N}，其中W表示不帶車輛調移的只取不送調車形式數量，種；E表示不帶車輛調移的只送不取調車形式數量，種；R表示不帶車輛調移的同時送取調車形式數量，種。

目標函數式 ⑴ 表示調車鉤數最優；公式 ⑵ 表示調機每日實際作業時間之和不超過每日調機v的最長限定作業時間；公式 ⑶ 表示只取不送和同時送取中送車列數必須滿足可以發出列車列數；公式 ⑷ 表示只送不取和同時送取中送車列數不能超過到達列車列數；公式 ⑸ 表示站內到發線數量約束，且至少要有一條供調機走行的空閑到發線；公式 ⑹ 表示每臺調機可處理的鉤數不超過每日調機可處理的調車鉤數最大能力限制；公式 ⑺ 表示多臺調機同時作業時，最多由一臺調機處理車輛調移作業。

1.3 模型求解

考慮作業時間的區段站調車鉤數分配模型中決策變量是ziv，該變量是整數變量，因而該模型為整數規劃模型，采用分支定界算法有較好的求解效率。下面對算法節點、分支過程和算法求解步驟分析如下。

（2）算法求解步驟。算法根據初始可行解作為初始下界開始分支，并以調機類型指標作為剪支規則進行剪支、迭代與優化，最終獲得最優的調車鉤數。算法中符號定義如下：z*為當前最優解；DB*為當前最優解的目標函數值，求得最優調車鉤數目；Cn為可行節點集合，用以記錄算法中經定界得到的可行節點；Cn'為分支節點集合，用以記錄算法中分支得到的節點；為表示當前節點的目標函數值，即在當前節點已經統計的最優調車鉤數。具體算法步驟 如下。

步驟1：初始化。根據公式(1)至公式(7)容易找出一個滿足所有約束的初始解。生成根節點，將根節點放入集合Cn中，并設置當前最優解z*為該初始解，當前下界為DB*，轉步驟2。

步驟2：分支。若集合Cn中無可進行分支的節點，算法結束；否則，對于集合Cn中未進行分支的節點，根據其選擇的調機類型進行分支生成一組子節點，將其中各節點的父節點記錄為Ovk；將節點Ovk標記為已分支，轉步驟3。

步驟3：定界。對于步驟2生成的一組節點Cn'，取出其中一個節點統計得到最優調車鉤數，進行以下操作：如果，轉步驟4；如果，轉步驟5；如果，轉步驟2。

步驟4：剪支。刪除按當前節點，轉步驟3。

步驟5：找到可行節點。更新當前最優解z*和當前最優下界DB*；根據父節點信息生成當前最合理的調車形式統計次數；將該節點標記為已分支，并找到可行節點，將當前節點加入Cn，轉步驟3。

2 算例分析

2.1 參數設置

為了驗證提出的考慮作業時間的區段站調車鉤數分配模型和求解算法的有效性，以山東東北部龍口港站為例，根據問題描述及模型參數設置。已知該區段站共計有6種調車形式。K = 2時，ΩK集合包含只取不送和帶車輛調移的只取不送2種調車形式，分別用i = 1和i = 2表示；M = 2時，ΩM集合包含只送不取、帶車輛調移的只送不取2種調車形式，分別用i = 3和i = 4表示；N = 6時，ΩS集合包含同時送取和帶車輛調移的同時送取2種調車形式，分別用i = 5和i = 6表 示； W = 1，E = 1和R = 1時，ΩD集 合包含i = 2和i = 4和i = 6共3種調車形式；ΩN集合包含全部i = 1至i = 6共計6種調車形式。該區段站由2個調車組負責調車作業，并為每個調車組分別配有 1臺同類型調機，因而V = 2，ΩV集合包含v = 1和 v = 2共2臺調機。根據調機摘車或掛車作業的行程，可以得到不同調車形式下的調車鉤數和標準作業時間如表1所示。考慮調車人員作業前準備、作業休息及調機保養等因素調機v每日最長限定作業時間T1和 T2都為30 000 s，每日貨物線已裝載完成可以發出的車列數A為6列，每日根據列車運行圖統計的到達車列數B為6列，站內到發線的數量C為6條，每臺調機最大工作能力限制Q1和Q2都為20鉤。

表1 調車鉤數和標準作業時間Tab.1 Number of shunting hooks and standard working time

2.2 模型求解與分析

利用分支定界算法對建立的調車鉤數最優單目標模型進行求解，可以求得模型目標函數值 ，即調車鉤數最優為35鉤，其對應的調機v處理調車形式i的數量ziv和鉤數zivLi的最優方案如表2所示。

由表2分析可知，根據調機最長限定作業時間，到達車列數、發出車列數及站內到發線數等限制條件可以預估出調機v處理調車形式i的次數和鉤數，方便車站調度員進行調車作業計劃制訂；其次調機2在調車作業中帶車輛調移的調車形式共選擇了3次，可以看出相較于不帶車輛調移的調車形式，帶車輛調移的調車形式更容易被優先選擇，優先執行，這是由于帶車輛調移的調車形式會更節省車輛取送過程中的走行時間，在更少的時間內完成更多鉤數。另外，求得調機v處理調車形式i花費時間的最優方案如表3所示。

表2 調機v處理調車形式i的數量ziv和鉤數ziv Li的最優方案Tab.2 Optimal number and hook number of shunting type i handled by shunting locomotive v

表3 調機v處理調車形式i花費時間的最優方案 sTab.3 Optimal time spent by shunting type i handled by shunting locomotive v

由表3分析可知，在區段站調車鉤數統計模型中考慮作業時間可以得出調機v處理調車形式i花費的時間，在每日最長限定作業時間Tv= 30 000 s的限制下，對調車形式i進行組合選擇，使調機1和調機2 的作業時間更加均衡。調機1和調機2實際作業時間與作業總時間各相差240 s和265 s，優化結果能夠提高調車人員作業效率，側面驗證了考慮作業時間的區段站調車鉤數分配模型的有效性。

根據模型求解結果，調機的最長限定作業時間Tv是影響調車鉤數分配和調車人員積極性的重要因素，為了分析調機最長限定作業時間不同時對調車鉤數和調機實際作業時間的影響，令調機最長限定作業時間在區間[25 000，35 000]中取值，間隔1 000 s， 即共分為11種情形，對算例進行敏感性分析，得到調機對應的調車鉤數和實際作業時間分配結果如圖1所示。

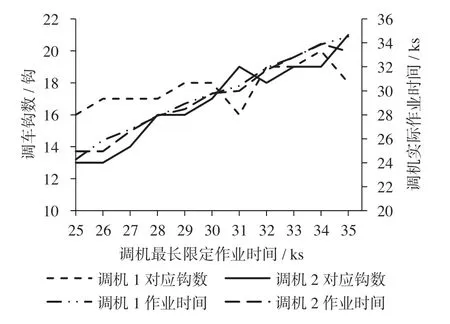
圖1 調機對應的調車鉤數和實際作業時間分配結果Fig.1 Number of shunting hooks and actual working time

由圖1分析可知，隨著調機最長限定作業時間的增多，每臺調機處理的調車鉤數也不斷增多，調機實際作業時間也不斷增加；調機1與調機2處理的調車鉤數大致相同，最大相差4鉤，同時可以看出每臺調機對應的實際作業時間大致吻合，從而表明該模型能夠為每臺調機所對應的調車人員分配合適的調車作業任務，保證作業合理性。

3 結束語

調車鉤數分配分析對合理制訂調車作業計劃有重要的現實意義。將作業時間考慮到區段站調車鉤數分配模型中，能夠保證在調車鉤數最優的情況，兼顧調車作業公平合理，該模型驗證了帶車輛調移的調車形式會被優先選擇，間接證明該種調車形式對提高調車作業效率有積極意義。作業時間變化會對調車鉤數分配產生一定影響，不論作業時間如何變化，基于作業時間的區段站調車鉤數分配模型能保證每位調車人員作業時間的均衡。在實際作業中，因車輛裝載超噸、車輛技術問題及車輛混編等情況經常發生，今后應將這些因素考慮到調車鉤數分配模型研究中。