基于BAS算法的配電網無功優化
董煜 王小會 李曉青


摘? 要:配電網無功優化是保證其經濟安全運行的重要措施。針對配電網無功優化問題,文章提出基于天牛須搜索算法的配電網無功優化策略,同時,引入自適應變化的步長因子改善BAS算法的迭代速度。最后,在Matlab中引入IEEE33節點配電網系統對基于粒子群算法、天牛須搜索算法和改進天牛須搜索算法的無功優化策略進行仿真驗證并做對比分析,仿真結果表明,基于改進天牛須搜索算法的無功優化策略性能更優。
關鍵詞:配電網;無功優化;粒子群算法;天牛須搜索算法
中圖分類號:TM761+.1;TP18? ? ? ?文獻標識碼:A 文章編號:2096-4706(2021)01-0055-03
Reactive Power Optimization of Distribution Network Based on BAS Algorithm
DONG Yu,WANG Xiaohui,LI Xiaoqing
(Lanzhou Institute of Technology,Lanzhou? 730050,China)
Abstract:Reactive power optimization of the distribution network is an important measure to ensure its economic and safe operation. In view of the reactive power optimization problem of distribution network,a reactive power optimization strategy based on the beetle antennae search algorithm is proposed in this paper. At the same time,it introduces an adaptively changing step size factor to improve the iteration speed of the BAS algorithm. Finally,the IEEE33-node distribution network system is introduced in Matlab to simulate and verify the reactive power optimization strategy based on the particle swarm optimization algorithm,the beetle antennae search algorithm,and the improved beetle antennae search algorithm. The simulation results show that the performance of the reactive power optimization strategy based on the improved beetle antennae search algorithm is better.
Keywords:distribution network;reactive power optimization;particle swarm optimization algorithm;beetle antennae search algorithm
0? 引? 言
配電網是電力系統的關鍵組成部分,能夠對電能進行分配。電力系統不僅要求能夠穩定可靠的運行,還要降低能源的損耗,提高系統的經濟性。電網無功優化就是對其無功潮流進行優化,改善其分布,達到提高節點電壓水平,降低運行損耗的目的,從而保證整個系統安全、可靠、經濟的運行[1]。配電網無功優化問題是一個多變量、多約束的非線性規劃問題,求解過程十分復雜[2]。電力系統最優潮流的概念和模型在20世紀60年代被提出后,國內外研究人員便對此展開了大量的研究。目前,求解無功優化問題的方法有兩種類型:一是數學算法。胡驊等人根據雙層優化理論建立了以準入功率最大化為上層優化目標、滿足電壓約束為下層優化目標的計算模型[3]。程軍照等人在預測-校正內點法基礎上加入了直角坐標系進一步優化了無功優化計算模型[4]。但是這類算法對優化模型具有較高的要求,計算過程復雜,同時很難到達精度要求。二是人工智能算法。崔挺等人通過模糊動態聚類分析方法實現小生境群體的劃分來改善遺傳算法容易陷入局部收斂的特性進行無功優化的建模[5]。熊虎崗等人提出了基于免疫算法的多目標無功優化算法[6]。李如琦等人提出一種基于差分策略的粒子群算法對多目標電力系統無功優化進行求解[7]。張庭場等人提出了一種以年費用最小為目標函數的融合裂變和變異操作的分合群粒子群算法無功優化數學模型[8]。這類算法中以粒子群優化算法應用最為廣泛,但粒子群算法迭代過程簡單易于實現,在求解多峰問題時,易陷于局部最優,并且計算量大。
天牛須搜索算法(Beetle Antennae Search,BAS)是受天牛覓食啟發而生的一種智能優化算法,其不需要具體函數形式,不需要梯度信息,即可實現高效尋優[8-11]。相較于粒子群算法,天牛須搜索算法是單體智能優化算法,能夠簡化算法結構,并且計算量小、精度高。因此,基于天牛須搜索算法的無功優化具有其獨特的優勢,同時,在傳統天牛須搜索算法中引入例如非線性變步長因子,可以提高算法的收斂速度。
1? 配電網無功優化數學模型
綜合考慮系統網絡損耗,電容器購買及維護費用,電壓質量三個方面,建立以電壓不越限,年使用費用最小為目標的無功優化數學模型。其中,電壓越限作為懲罰函數出現在目標函數中。目標函數為:
(1)
式中:
(2)
(3)
有功功率與無功功率滿足等式約束:
(4)
無功補償量與節點電壓滿足不等式約束:
(5)
其中,β為市場電價,Ploss為系統網損,τmax為最大負荷利用小時數,Pi為第i個節點處注入的有功,Qi為第i個節點處注入的無功,Gij為節點i和j之間的電導,Bij為節點i和j之間的電導,δij為節點i和j之間的相角差,Qci為節點i的補償容量,Qcimin和Qcimax為節點i的最小補償容量和最大補償容量,Ui為節點處i的電壓幅值,Ucimin和Ucimax為節點i處電壓的下限與上限,ka為電容器的年維護費用率,ke為投資回收系數,kc為電容器的購買費用,λ為電壓越限懲罰系數,m為系統的補償點個數,n為系統的節點個數。
2? BAS算法
天牛須搜索在2017年被提出,也叫甲殼蟲須搜索。其基本原理為,天牛在覓食的時候不知道食物的具體位置,根據兩只觸角識別食物的氣味決定天牛的飛行方向,最終找到食物,這種覓食過程就是全局函數尋優。天牛須搜索算法可以實現高效尋優,在尋優過程中不需要具體的函數形式。
2.1? BAS模型
根據天牛須搜索算法原理建立了對應的BAS模型,過程如下:
(1)隨機方向向量。為了模擬天牛的搜索行為,定義它的方向向量為:
(6)
其中,rand為隨機函數,k為空間維數。
(2)天牛左右須空間坐標:
(7)
其中,t為迭代次數,xlt為天牛左須位置,xrt為天牛右須位置,d為天牛左須與右須之間的距離。
(3)適應度值:
(8)
其中,f( )為適應度函數,fleft表示在此刻的空間位置天牛左須的適應度值,fright表示在此刻的空間位置天牛右須的適應度值。
(4)步長因子:
δt=c1δt-1+δt0,dt=δt/c2? ? ? ? ? ? ? ? ? ? ? ? ?(9)
其中,δt表示天牛的搜索步長,表示天牛在初始時刻的步長因子,其值一般設置較大,以保證覆蓋當前的搜索區域,c1,c2則由使用者進行設置。
(5)預更新位置:
xt=xt-1+δt·sign(fleft-fright)? ? ? ? ? ? ? ?(10)
根據上式,天牛更新位置,其中,sign( )為符號函數。
(6)接受解的判斷規則:在BAS算法在迭代過程中,判斷更新位置處的適應度值與上一次的適應度值的大小,以確定是否接受預更新位置。
2.2? BAS算法的改進
BAS算法由步長因子決定算法的尋優能力,是算法收斂快慢的關鍵所在,步長因子取值較大,算法具有更好的全局搜索能力,但是收斂速度慢;反之步長因子取值較小,算法尋優的精度更好,但是易陷于局部極值。而BAS算法中的步長因子是固定值,難以滿足收斂速度與精度的要求,因此,提出了自適應變步長因子的BAS算法,其思路是:在迭代初始階段,采取較大的步長因子,使算法具有更好的全局尋優能力,加快尋優速度;在后期,減小步長因子,以保證解的精確性。新的步長因子公式為:
(11)
其中,δt為第t次迭代時的步長因子;δ0為初始化步長因子,取值為0.95;maxgen為總的迭代次數;b取值為2;a∈(0,1);ft為第t次迭代時的適應度值,ft為歷史最優的適應度值。公式說明:當第t次迭代所得適應度值大于歷史最優適應度值時,則認為尋優性能不好,減小步長因子,加快尋優速度;當第t次迭代所得適應度值不大于歷史最優適應度值時,則認為尋優性能良好,保持步長因子不變。
3? 算例驗證及分析
分別采用POS算法,BAS算法,改進BAS算法在Matlab中采用IEEE33節點配電網系統進行仿真驗證。在該系統中設
置2個補償點,補償點設置位置為{17,31},潮流計算采用
前推回代算法,設置收斂精度為10-6。BAS算法參數設置為:最大迭代次數maxgen=100,c1=0.995,c2=1;改進BSA算法參數設置為:最大迭代次數maxgen=100,c1=0.95,c2=1;
粒子群參數設置為:慣性權重系數w=0.729,權重因子c1= 2.05,權重因子c2=2.05,粒子群規模N=50,最大迭代次數maxgen=1 000。其他參數設置:市場電價β=0.5 元/千瓦·時,最大負荷利用小時τmax=5 000 h,電容器的年維護費用率ka=0.13,投資回收系數ke=0.1,電容器的購買費用kc=60 元/千乏,電壓越限懲罰系數λ=106。
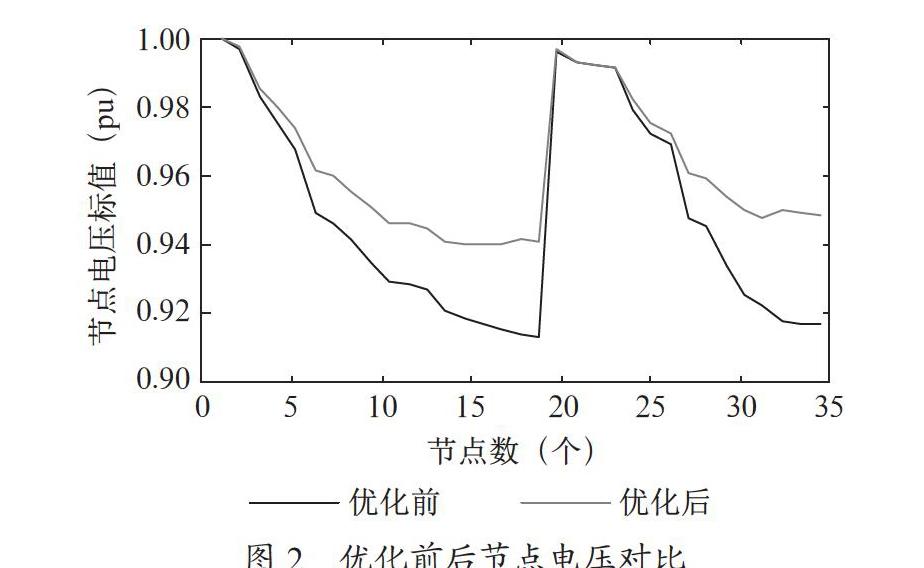
圖1為分別采用PSO,BAS,改進BAS算法對IEEE33節點配電網系統進行無功優化所得迭代曲線圖,由圖可見改進BAS算法相比于BAS算法尋優速度更快,但是兩個算法所需迭代次數都略高于PSO算法,這是因為粒子群算法是群體尋優算法,而BAS與改進BAS算法為單體尋優算法,從總的計算量上來計算改進BAS算法在第24次迭代即尋到了最優值,迭代次數即為計算量,而粒子群算法在第20次迭代即尋到了最優值,但等效計算量為迭代次數乘上粒子數量,計算量達到了1 000。可見,在計算量上,改進BAS算法遠遠小于PSO算法。圖2為優化前后的節點電壓對比圖,由圖可見,補償后,各節點電壓都有所提升,特別是電壓最低的節點,由0.912 8提升至0.943 3,系統網絡損耗下降30.93%,年費用下降30.18%。
表1是配電網系統補償前后指標的對比,可以看出,在節點電壓提升的基礎上,系統網絡損耗從204.10 kW降低到142.35 kW,下降了32.25%;年費用從51.02萬元降低到35.42萬元,下降了30.58%。仿真結果表明本文的優化方法是有效的,提高節點電壓水平,降低了運行損耗。
4? 結? 論
文章針對傳統粒子群算法配電網無功優化量大的缺點,提出了基于改進BAS算法配電網無功優化策略,同時提出自適應變步長因子改進BAS算法的尋優速度,并在Matlab中采用IEEE33節點系統對所提策略進行仿真驗證,得出:改進BAS算法相比于BAS算法具有更快的尋優速度,與PSO算法相比,計算量大大降低,對于配電網無功優化具有一定的借鑒意義。
參考文獻:
[1] 陳琳,鐘金,倪以信,等.含分布式發電的配電網無功優化 [J].電力系統自動化,2006(14):20-24.
[2] 王云,江全元.基于原對偶內點法和分枝定界算法的配網無功優化計算及其并行實現 [J].電力自動化設備,2013,33(2):52-56.
[3] 胡驊,吳汕,夏翔,等.考慮電壓調整約束的多個分布式電源準入功率計算 [J].中國電機工程學報,2006(19):13-17.
[4] 程軍照,李澍森,程強.一種無功優化預測校正內點算法 [J].電工技術學報,2010,25(2):152-157.
[5] 崔挺,孫元章,徐箭,等.基于改進小生境遺傳算法的電力系統無功優化 [J].中國電機工程學報,2011,31(19):43-50.
[6] 熊虎崗,程浩忠,李宏仲.基于免疫算法的多目標無功優化 [J].中國電機工程學報,2006(11):102-108.
[7] 李如琦,李芝榮,王維志,等.基于差分策略的多目標電力系統無功優化 [J].電網技術,2012,36(12):170-175
[8] 張庭場,耿光飛.基于改進粒子群算法的中壓配電網無功優化 [J].電網技術,2012,36(2):158-162.
[9] JIANG X Y,LI S. BAS:Beetle Antennae Search Algorithm for Optimization Problems [J].International Journal of Robotics and Control,2018,1(1):1-5.
[10] JIANG X Y,LI S. Beetle antennae search without parameter tuning (BAS-WPT) for multi-objective optimization [J].Filomat,2020,34(15):5113-5119.
[11] 王甜甜,劉強.基于BAS-BP模型的風暴潮災害損失預測 [J].海洋環境科學,2018,37(3):457-463.
作者簡介:董煜(1991—),男,漢族,河南許昌人,助教,碩士研究生,研究方向:電子信息工程。

