框架結構-樁筏基礎-地基共同作用時程分析
田丹丹 張富鈞
(甘肅交通職業技術學院,甘肅 蘭州 730070)
由于建筑物高聳,不僅豎向荷載較大、相對集中,且風荷載和地震荷載引起的傾覆力矩也成倍增長[1-2],因此,傳統理論和方法不能照搬于高層建筑[3]。同時,地震是主要自然災害之一,對工程結構進行抗震設計以降低地震危害非常必要。本文利用大型通用有限元軟件ANSY[4-5]建立不考慮共同作用的傳統模型和考慮共同作用的三維實體模型來研究上部結構-基礎-地基共同作用時的地震反應。
1 有限元模型的建立
本文的分析模型上部為一規則的空間框架結構,結構在X方向為5跨,Z方向為3跨,每跨跨度均為6m,結構高度方向為Y向,框架共9層,每層層高3.3m,各層框架柱截面尺寸為600mm×600mm,梁截面尺寸為300mm×700mm,梁的混凝土強度等級C30,柱的混凝土強度等級為C35。樓板為現澆鋼筋混凝土樓板,混凝土選用C30,板厚100mm,樓面活荷載為2kN/m2,框架梁上均布6kN/m的線荷載,以模擬填充墻的自重荷載。基礎采用樁筏基礎,筏板厚度為600mm,樁徑600mm,樁長15m,土體為黃土。共同作用有限元模型如圖1。
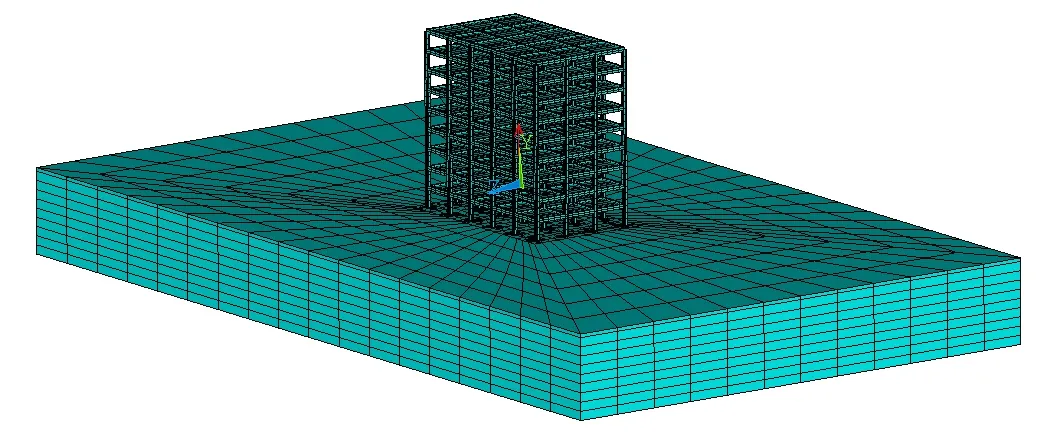
圖1 共同作用有限元模型
2 地震波的輸入
對建立的模型進行地震作用下的動力性能分析,并將兩者進行比較。進行時程分析時,GB 50011-2010《建筑抗震設計規范》規定應按建筑場地類別和設計地震分組選用不少于二條實際地震記錄和一條人工模擬的加速度時程曲線[6],由于缺少附近場地的實際地震記錄,本文采用埃爾森特羅(El-Centro)波進行分析。埃爾森特羅波的最大加速度值為3.417m/m2,時間取8秒。分析時按照我國抗震規范規定,將埃爾森特羅波的最大加速度幅值調至常遇地震時的加速度,峰值為0.7m/m2。
3 傳統模型與共同作用模型地震反應分析與對比
3.1 位移的分析與對比
為了比較兩種模型在地震作用下的響應,提取傳統模型以及共同作用模型中結構(以角柱為例)在頂層、6層以及3層時的X方向的位移時程曲線,見圖2-圖5。
從圖2-圖4可以看出,在考慮共同作用的模型中,樓層的最大位移值比傳統模型的位移值有所增大,其原因主要是考慮了下部的基礎和地基后,結構的位移受基礎和地基產生平移、基礎轉動以及結構本身的變形等因素的影響。基礎的平移以及地基剛性的減弱(與傳統模型相比)使得樓層的最大位移有所增大。基礎與地基的剛度越小,結構的水平位移會增大得越多。
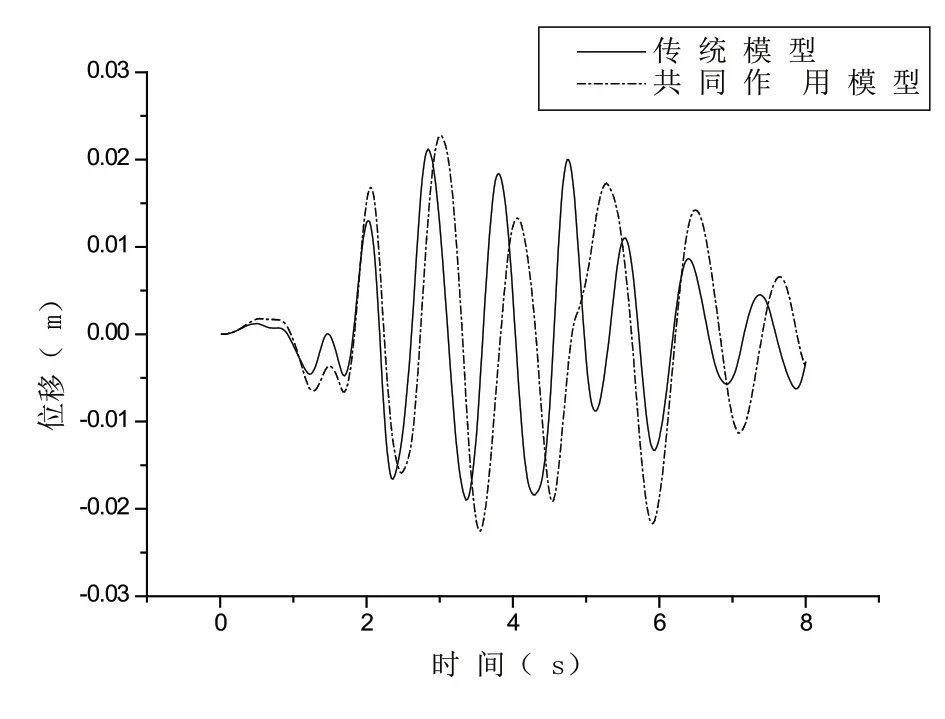
圖2 角柱頂層時程位移對比圖
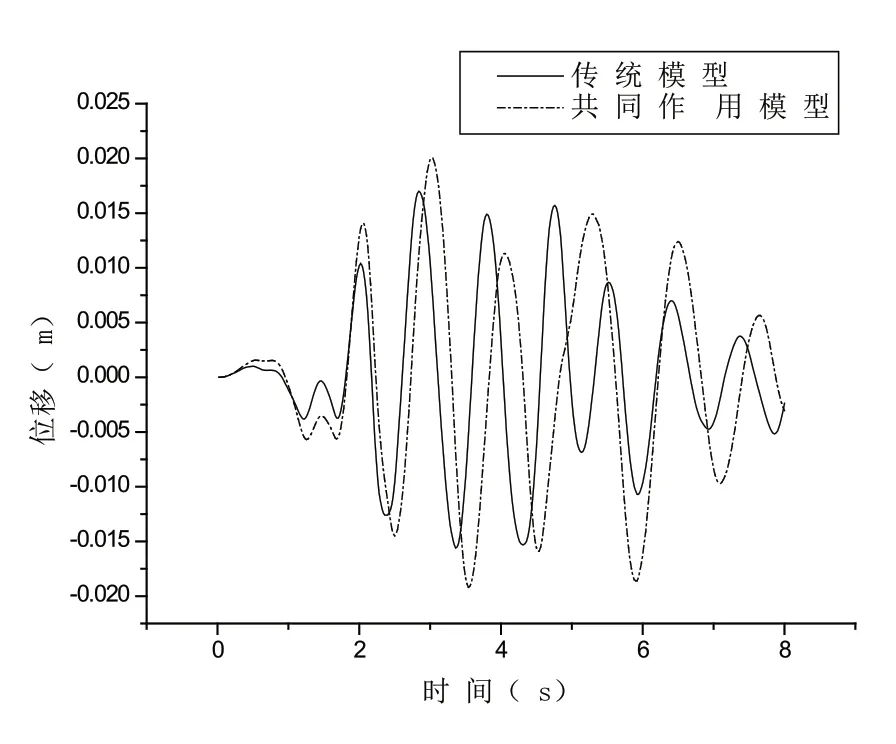
圖3 角柱6層的時程位移對比圖
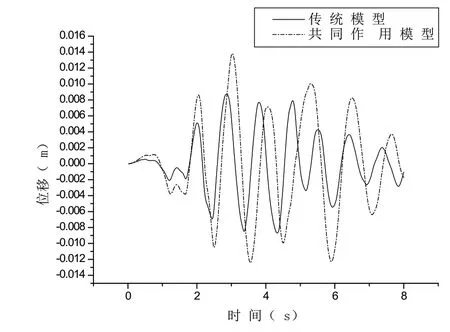
圖4 角柱3層的時程位移對比圖
傳統模型中,角柱的最大位移發生在9層頂,最大值21.2mm,出現的時間約為2.84秒;共同作用模型中,角柱的最大位移也發生在9層頂,最大值22.8mm,出現的時間約為3.02秒。由此可見,在傳統模型和共同作用模型的情況下,最大位移發生的位置是一致的。將角柱各層的最大位移提取出來,并將相關結果以圖形的形式表現在圖5中,可以清楚看到結果。
從圖5可見,在埃爾森特羅波作用下,共同作用模型的層位移與傳統模型的層位移相比有所增大,但通過計算層間最大位移發現,共同作用模型的層間位移與傳統模型的層間位移相比稍小,說明考慮共同作用可減少上部結構內的次應力,也就是說考慮共同作用后對整體結構是有利的。
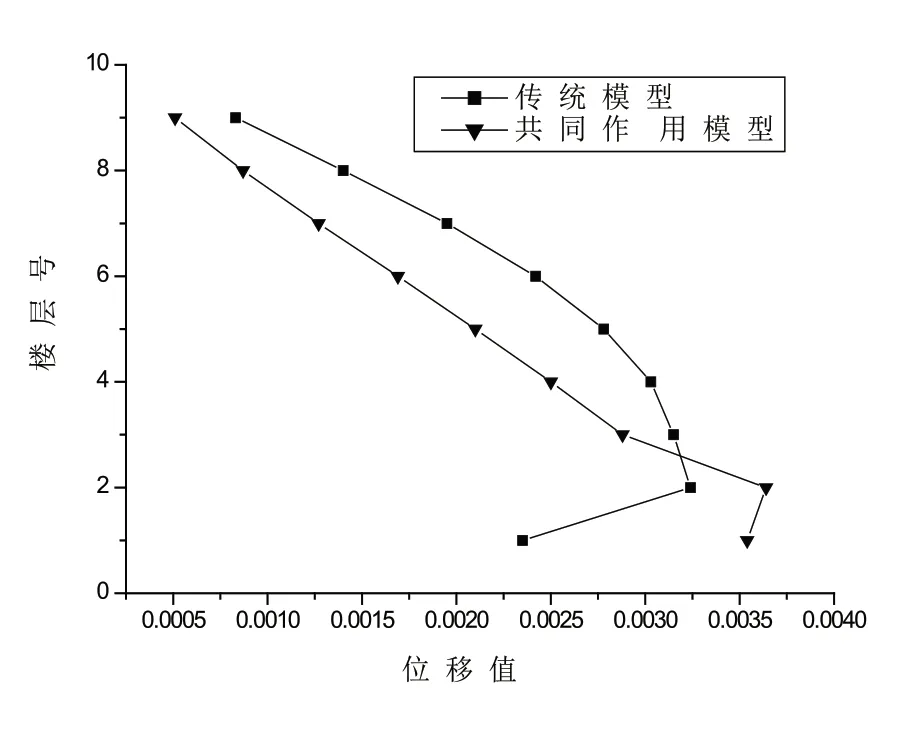
圖5 角柱層間最大位移對比曲線
在正常使用條件下,建筑結構應具有足夠的剛度,以避免產生過大的位移而影響結構的各種使用要求。同時,結構樓層的抗側剛度是影響結構層間位移的主要因素,抗側剛度可以通過層間變位角來表示。層間變位角是層間最大位移與層高的比值,由層間變位角可知結構的薄弱層位置。在埃爾森特羅波的作用下,傳統模型層間最大位移發生在第二層,其最大值為3.24mm,層間最大轉角為1/1018,可見此層為結構的薄弱層,層間最大轉角比JGJ 3-2010《高層建筑混凝土結構技術規程》中的限值1/550小,說明此結構滿足抗震性能的要求。共同作用模型的最大位移仍然發生在第二層,其最大值為3.64mm,說明兩種情況下結構的薄弱層出現的位置基本相同。
3.2 剪力的分析與對比
在埃爾森特羅波作用下,將兩種模型角柱的最大剪力提取出來,將這些剪力值繪成曲線圖的形式,如圖6。可以看出,考慮共同作用后,柱的剪力明顯減小。
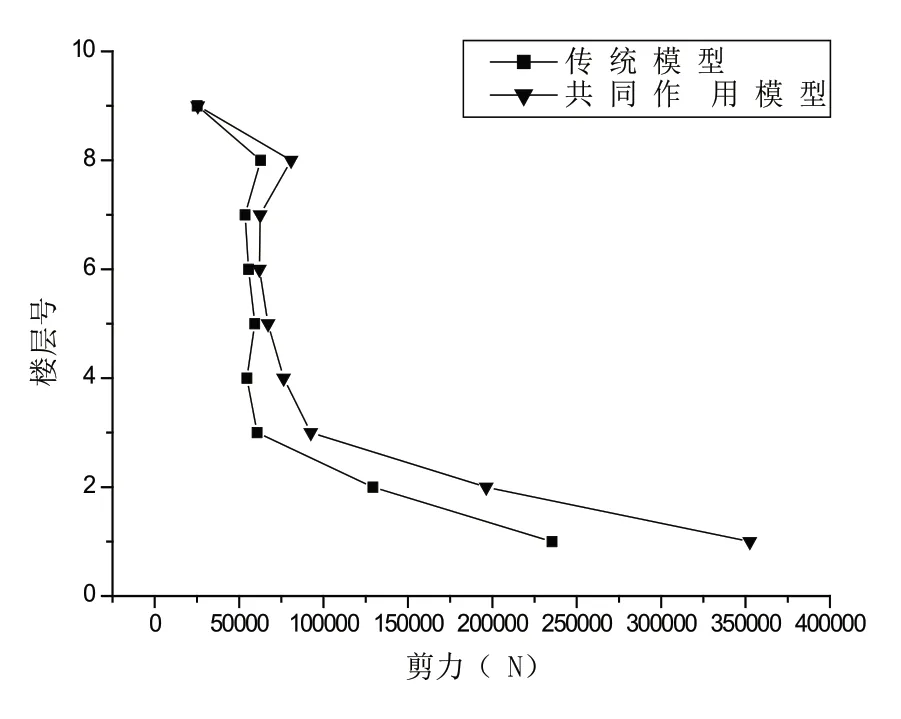
圖6 角柱最大剪力對比圖
由圖6可以看到,在層數較低時,共同作用模型柱剪力比傳統模型柱剪力小30%左右;隨著層數的增加,兩者柱剪力逐漸接近,剪力減少的越來越少,但總體來說,考慮共同作用后,柱的剪力仍然是減小的,也即對上部結構是有利的。
4 結論
對兩種模型進行水平地震作用下的時程分析,主要結論如下:考慮共同作用模型與傳統模型相比,在地震作用下,上部框架結構樓層最大位移和樓層最大剪力都有所增大,而樓層的層間位移有所減小,說明在一定情況下考慮共同作用后對結構整體是有利的。

