考慮中介軸承彈流潤滑時雙轉子系統振動特性

李 靜,曹樹謙,郭虎倫,聶日敏,侯遠航

(1.天津大學 機械工程學院,天津 300354； 2.天津市非線性動力學與控制重點實驗室(天津大學),天津 300354；3.天津大學 力學國家級實驗教學示范中心，天津 300354)

為了提高推重比、改善氣動穩定性，現代航空發動機多采用雙轉子結構.中介軸承作為聯系高低壓轉子的關鍵部件，由于工作時內外圈轉速大、環境溫度高、潤滑條件難以保證，因此也是雙轉子系統中的薄弱環節.隨著軸承零件幾何誤差和工藝缺陷的降低，潤滑對軸承及轉子系統振動的影響已日顯重要.潤滑油在軸承中將鋼球和滾道兩接觸體分離，不僅可以起到降溫的作用，還會改變轉子系統的振動特性.因此分析中介軸承處的彈流潤滑作用對航空發動機雙轉子系統動力學特性的影響是非常必要的.

國內外學者運用多種建模方法以及不同的數值求解手段，針對中介軸承-雙轉子系統動力學響應，進行了一系列研究. Ferraris等[1]利用拉格朗日方程建立雙轉子模型，利用有限元方法預測系統動力學行為.Chen[2]建立轉子-球軸承-機匣耦合動力學模型，轉子和機匣系統用有限元方法建模，支承系統采用集中參數法建模，用Newmark-β方法以及翟方法對系統響應進行求解，結果表明提出的模型可有效仿真航空發動機的振動特性.Hu等[3]建立了五自由度雙轉子模型，采用Runge-Kutta-Fehlberg算法進行求解.此外，白雪川[4]對反向旋轉雙轉子系統，開展了機動飛行實驗.張天程等[5]分析了碰摩狀態下，雙轉子系統的彎曲振動和扭轉振動.Wang等[6]重點考慮了中介軸承對雙轉子系統動力學特性的影響.Gao等[7]建立了中介軸承的局部缺陷模型并對雙轉子系統的非線性響應進行了分析.Sun等[8]用MHB-AFT方法分析了碰摩情況下雙轉子系統的穩態響應.Hou等[9]應用HB-AFT方法對雙轉子系統中的主共振進行了研究.

彈性流體動力潤滑(Elastohydrodynamic lubrication, EHL)，簡稱彈流潤滑，是將Reynolds潤滑理論和Hertz彈性接觸理論相結合，研究滾動或滾滑條件下彈性體之間的流體動力潤滑特性.在球軸承中，滾珠和滾道之間一般處于彈流潤滑狀態[10].張彤等[11]以球軸承為研究對象，求解了滾動體和內外圈在彈流潤滑狀態下的剛度和阻尼，分析了軸承不同轉速和游隙對轉子系統動態特性的影響，研究表明具有動態剛度和阻尼的軸承-轉子系統動力學特性更加復雜.張俊紅等[12]研究了彈流潤滑作用下，轉子-滾動軸承系統在碰摩和不對中耦合故障狀態下的動力學響應，并在實驗臺進行驗證，結果表明考慮彈流潤滑理論的模型比未考慮彈流潤滑理論的模型更能準確體現耦合故障系統的振動響應.王占彬等[13]基于點接觸的彈流潤滑理論，利用數值方法求解了軸承-轉子系統的動力學微分方程，通過不同參數條件下的軸心軌跡、相圖、分岔圖等，分析了轉子系統的動力學特性.田晶等[14]考慮了彈流潤滑影響和時變位移激勵，提出一種帶局部缺陷的中介軸承動力學模型，通過實驗驗證結果表明，提出模型能準確模擬中介軸承在不同狀態和不同缺陷尺寸下的振動響應.

上述研究大都針對彈流潤滑作用對軸承或單轉子系統的影響，而雙轉子系統中介軸承處普遍存在彈流潤滑作用.目前關于考慮中介軸承彈流潤滑作用時雙轉子系統動力學特性的研究較為欠缺.

本文以航空發動機雙轉子系統為研究對象，建立了考慮中介軸承彈流潤滑影響的中介軸承-雙轉子系統動力學模型，采用龍格庫塔法求解，對雙轉子系統的動力學特性進行分析，通過與不考慮彈流潤滑影響的雙轉子系統比較，研究了彈流潤滑作用對雙轉子系統動力學特性的影響.

1 系統建模

1.1 雙轉子系統建模

如圖1所示，建立含中介軸承的4點支承航空發動機雙轉子系統模型.

圖1 雙轉子系統模型

低壓系統包括無質量的彈性轉軸、剛性圓盤和1#、4#支承，軸頸質量分別為m1、m3和m4，軸段L1、L2和L3對應的剛度為k5、k6和k7，圓盤質量為m2，圓盤偏心距為s2，1#、4#支承處采用滾動軸承和彈性支承結構，簡化為彈簧阻尼系統，剛度和阻尼分別為k1、k4和c1、c4.高壓轉子考慮為剛性轉子，因此高壓系統包括無質量的剛性轉軸、剛性圓盤和2#支承，圓盤質量為m5，圓盤偏心距s5，2#支承處同樣采用滾動軸承加彈性支承結構，簡化后的剛度和阻尼為k2和c2.高低壓轉子定轉速比反向旋轉，低壓轉子轉速為ω1，高壓轉子轉速為ω2.忽略圓盤的偏轉和陀螺力矩，系統包括10個自由度.

根據轉子動力學理論和集中質量法，得系統動力學方程：

(1)

質量mi(i=1,2,3,4,5)對應的坐標為(zi,yi)，系統的廣義坐標矢量q為

(2)

質量矩陣M、剛度矩陣K、阻尼矩陣C分別為：

(3)

其中：

廣義力矢量F為

F=Fb+G+Fs,

(4)

其中:Fb為中介軸承力矢量,即

G為重力矢量，即

1.2 中介軸承力模型

考慮中介軸承為滾珠軸承，理想中介軸承幾何模型如圖2(a) 所示，根據Hertz接觸變形理論，球軸承的支反力可表示為[15]

F=kδ3/2.

(5)

其中：k為接觸剛度，δ為滾動體表面接觸點的彈性變形量.

第j個滾動體的徑向彈性接觸變形δj可表示為

δj=(yi-yo)cosθj+(zi-zo)sinθj-δ0.

(6)

式中：zi、zo、yi、yo分別為中介軸承內、外圈在水平和豎直方向的位移分量；δ0為中介軸承的徑向間隙；θj為任一時刻滾動體的運動位置角度，可表示為：

(7)

(8)

式中：Nb為滾動體數量；ωc滾動體公轉角速度；Ri、Ro分別為中介軸承內、外滾道半徑.

第j個滾動體與滾道之間的恢復力可表示為

(9)

其中

因此，中介軸承力為

(10)

1.3 中介軸承彈流潤滑接觸模型

當軸承中存在潤滑時，接觸剛度由變形剛度和油膜剛度組成.在Hertz接觸模型基礎上，考慮中介軸承油膜剛度和阻尼，建立如圖 2(b) 所示的彈流潤滑接觸動力學模型.接觸區域分為潤滑劑入口區、Hertz接觸區和潤滑劑出口區. 潤滑劑從入口區被帶入Hertz接觸區，經油膜擠壓后再從出口區流出. 3個區域的接觸特性可簡化為彈簧和阻尼結構.Hertz接觸區油膜黏性阻尼數值較小，對軸承影響可忽略不計，并且出口區的油膜氣穴形成的負壓對接觸特性影響較小，因此忽略Hertz接觸區的油膜阻尼以及出口區的油膜剛度和阻尼.這樣，中介軸承總的接觸剛度為Hertz接觸區的Hertz接觸剛度和油膜接觸剛度串聯，再與潤滑劑入口區的油膜剛度并聯；總的阻尼即為入口區的油膜黏性阻尼.

圖2 考慮彈流潤滑作用的中介軸承模型

Hertz接觸區的油膜剛度[16]為

(11)

式中：E′為等效彈性模量；Rx為當量曲率半徑；U為量綱一的速度參數；G為量綱一的材料參數；W為量綱一的載荷參數；kr為橢圓率，可表示為接觸橢圓長半軸a與短半軸b之比.

(12)

式中：u為軸承卷吸速度；η0為潤滑劑黏度；a1為滑油黏壓系數；Q為接觸載荷； ∑ρi、∑ρo分別為滾珠與內、外滾道接觸的主曲率和；Db為滾珠直徑；di、do分別為內、外環滾道直徑；ri、ro分別為內、外環溝曲率半徑；下標o和i分別表示軸承外圈參數和軸承內圈參數.

外圈入口區的油膜剛度[16]為

(13)

內圈入口區的油膜剛度為

(14)

外圈入口區的阻尼為

(15)

內圈入口區的阻尼為

(16)

中心油膜厚度h0可表示為

h0=RxHmin,

(17)

其中Hmin最小油膜厚度為

Hmin=3.63U0.68G0.49W-0.073(1-e-0.68kr).

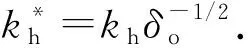
因此Hertz接觸區油膜力為

(18)

Hertz接觸區總剛度為

(19)

根據串聯彈簧受力相同，Hertz接觸區總變形可表示為

(20)

因此，

(21)

Hertz接觸區軸承力為

(22)

根據并聯彈簧變形量相等，即油膜入口區與Hertz接觸區彈簧變形量相等，定義：

(23)

則

(24)

考慮軸承油膜剛度影響的第j個滾動體與外滾道之間的恢復力可表示為

(25)

與以上推導類似，考慮軸承油膜剛度影響的第j個滾動體與內滾道之間恢復力可表示為

錄播教室是多媒體教室的一種。錄播教室通過錄播系統把現場攝錄的音視頻及多媒體電腦的畫面進行同步錄制，生成標準化的流媒體文件。錄播教室就是信息化教學的具體應用。

(26)

將滾動體與內滾道、外滾道接觸的剛度和阻尼看作串聯關系，如圖3所示，由復剛度方程式[18]得到總的剛度k和阻尼c為

圖3 接觸副剛度-阻尼模型

(27)

綜上所述，考慮彈流潤滑接觸模型后的中介軸承力為

(28)

與不考慮彈流潤滑作用的中介軸承力相比，考慮彈流潤滑作用后改變了中介軸承接觸剛度k并且增加了阻尼項.

1.4 系統方程無量綱化

在系統動力學方程 (1) 中引入量綱一的變換：

τ=ω1t,

(29)

(30)

(31)

(32)

得系統量綱一的方程：

(33)

其中：

式中：ξ為量綱一的阻尼矩陣；κ為量綱一的剛度矩陣；f為量綱一的力矢量.

1.5 系統參數選取

設定高低壓轉子反向旋轉，轉速比λ固定，取λ=-1.3.取接觸載荷Q為常數[19].由于非線性中介軸承力的存在，本文采用四階變步長龍格-庫塔法對方程(33)進行數值求解，系統計算參數[20]見表1.

表1 系統計算參數

2 動力學特性分析

2.1 雙轉子系統幅頻響應特征

(34)

其中:

式中kb為軸承線性化剛度，線性化方法詳見文獻[21].

求得前兩階臨界轉速分別為ω01=1 126 rad/s、ω02=2 930 rad/s，系統坎貝爾圖如圖4所示.一階主共振A點ω1=866 rad/s由高壓轉子不平衡引起，一階主共振B點ω1=1 126 rad/s由低壓轉子不平衡引起，二階主共振C點ω1=2 254 rad/s由高壓轉子不平衡引起，二階主共振D點ω1=2 930 rad/s由低壓轉子不平衡引起.由于高低壓轉子均存在不平衡激勵，因此每一階臨界轉速會出現兩個共振峰.

圖4 系統坎貝爾圖

圖5為中介軸承-雙轉子系統的幅頻響應曲線，采用ri和ro分別表示低壓轉子和高壓轉子的振幅.

圖5 中介軸承-雙轉子系統幅頻曲線

(35)

當不考慮彈流潤滑的影響時，低壓轉子的幅頻響應曲線在轉速860、1 120、2 220、2 940 rad/s處出現共振峰.與坎貝爾圖得到的臨界轉速對應.轉速860 rad/s處的第1個共振峰是高壓轉頻激發的一階共振，轉速1 120 rad/s處的第2個共振峰是低壓轉頻激發的一階共振，轉速2 220 rad/s處的第3個共振峰是高壓轉頻激發的二階共振，轉速2 940 rad/s處的第4個共振峰是低壓轉頻激發的二階共振.高壓轉子與低壓轉子的響應有類似規律.

當考慮中介軸承彈流潤滑作用的影響后，低壓轉子和高壓轉子響應一階共振峰無明顯變化，但二階共振峰均向右移動，并且在共振峰處振幅減小.低壓轉子和高壓轉子的響應規律一致.

2.2 中介軸承赫茲接觸剛度對系統特性的影響

研究中介軸承彈流潤滑作用下，中介軸承赫茲接觸剛度變化對低壓轉子和高壓轉子幅頻響應的影響.圖6為中介軸承赫茲接觸剛度分別為1×109、5×108、2×109N·m-1.5時，低壓轉子和高壓轉子的幅頻響應曲線.從幅頻曲線來看，赫茲接觸剛度增大，一階共振峰無明顯變化，二階共振峰向右移動且共振峰幅值減小，低壓轉子和高壓轉子響應規律一致.表2、3分別給出了低壓轉子和高壓轉子在不同中介軸承赫茲接觸剛度的情況下，考慮彈流潤滑作用與不考慮彈流潤滑作用相比，振動幅值的相對改變量.在一階共振峰處，振幅改變小于5%，由于轉速較低時系統整體振幅較小，因此幅頻曲線無明顯變化.在二階共振峰處振幅改變較明顯，相對改變量在4%～8%之間.低壓轉子和高壓轉子的一階共振峰位置均未發生偏移，而二階共振峰向高頻移動2%～7%，見表4、5.

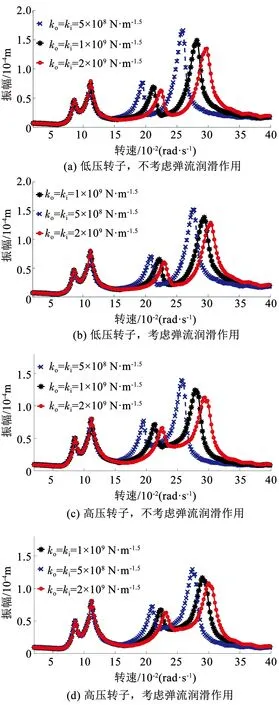
圖6 不同赫茲接觸剛度時雙轉子系統幅頻曲線

表2 低壓轉子振動幅值相對改變量

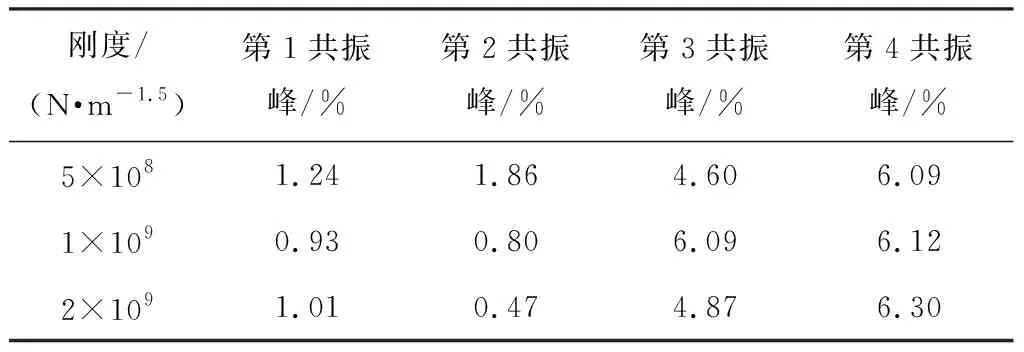
表3 高壓轉子振動幅值相對改變量

表4 低壓轉子共振峰位置對應的轉速相對改變量

表5 高壓轉子共振峰位置對應的轉速相對改變量

2.3 中介軸承徑向游隙對系統特性的影響

考慮中介軸承彈流潤滑的條件下，分析中介軸承徑向游隙變化對低壓轉子和高壓轉子幅頻響應的影響.圖7為徑向游隙分別為δ0=0.1×10-6m，δ0=2.0×10-6m和δ0=5.0×10-6m情況下，低壓轉子和高壓轉子的幅頻響應曲線.隨著徑向游隙增大，一階共振峰無明顯變化，二階共振峰沿轉速軸向左移動，并且中介軸承非線性特性在高壓轉子和低壓轉子的幅頻響應中表現明顯.

表6、7分別給出了低壓轉子和高壓轉子在不同中介軸承徑向游隙的情況下，考慮彈流潤滑作用與不考慮彈流潤滑作用相比，振動幅值的相對改變量.

在一階共振峰處，振幅改變小于4%，在二階共振峰處振幅改變較明顯，相對改變量在4%～9%之間.低壓轉子和高壓轉子一階共振峰位置對應的轉速未發生改變，而二階共振峰位置對應的轉速改變2%～8%，見表8、9.

表7 高壓轉子振動幅值相對改變量

表8 低壓轉子共振峰位置對應的轉速相對改變量

2.4 潤滑油黏度對系統特性的影響

在潤滑油黏度范圍0.002～0.400 Pa·s內，分別取潤滑油黏度為0.003、0.030、0.300 Pa·s，計算一階和二階共振峰處低壓轉子和高壓轉子的振動幅值，以及考慮彈流潤滑作用后轉子振動幅值的相對改變量，見表10、11.

表9 高壓轉子共振峰位置對應的轉速相對改變量

表10 低壓轉子振動幅值及振幅相對改變量

表11 高壓轉子振動幅值及振幅相對改變量

從表中可看出，考慮彈流潤滑作用的影響后，一階共振峰處振動幅值相對改變量較小，二階共振峰處振動幅值相對改變量較大.不同潤滑劑黏度對高低壓轉子振動幅值影響小于1%.并且潤滑劑黏度越高，低壓轉子和高壓轉子的振動幅值越小.這是由于潤滑劑黏度越高，其阻尼作用越大，因此減振效果越好.此結論與文獻[22]中利用實驗方法研究潤滑油黏度對軸承振動影響的結論一致.

3 實驗研究

利用雙轉子振動特性實驗臺對比研究考慮中介軸承彈流潤滑作用和不考慮中介軸承彈流潤滑作用時雙轉子系統的動力學特性.

3.1 實驗裝置

實驗裝置如圖8所示，主要包括氣體驅動雙轉子實驗臺、空氣壓縮機、高低壓渦輪進氣控制閥、油霧潤滑系統、TST數據采集系統、直流電源、前置器、電渦流傳感器、計算機、TST動態測試分析軟件.

圖8 實驗裝置

氣體驅動雙轉子實驗臺是根據某型航空發動機的整機結構簡化而來的，包括低壓轉子、高壓轉子以及中介軸承等支承結構[23].為了最大限度地接近真實工況，高壓轉子和低壓轉子均通過氣體驅動渦輪旋轉進而帶動轉子結構旋轉，高低壓轉子反向旋轉，轉速比可隨意設定，此處控制高低壓轉子轉速比為-1.3.并且實驗臺是可拆裝的，可以更換中介軸承.

空氣壓縮機為雙轉子實驗臺提供動力；高低壓渦輪進氣控制閥可控制進氣量，進而控制高低壓轉子的轉速；油霧潤滑系統提供潤滑和冷卻作用；直流電源和前置器配合使用，為電渦流傳感器提供交變電流；TST數據采集系統、TST動態測試分析軟件和計算機可對傳感器的輸出信號進行記錄、顯示和分析.實驗系統框圖如圖9所示.

圖9 實驗系統框圖

3.2 實驗結果

在中介軸承兩種不同工況下，分別進行雙轉子系統振動實驗.1)洗凈中介軸承潤滑油，并關閉油霧潤滑系統；2)中介軸承充分潤滑，并打開油霧潤滑系統.

圖10為低壓轉子轉速314 rad/s，高低壓轉速比為-1.3的工況下，高壓轉子的軸心軌跡圖.對比圖10(a) 、10(b) 可以發現在中介軸承充分潤滑的工況下，轉子軸心軌跡的范圍更小，即轉子系統的振動減小.

圖10 高壓轉子軸心軌跡

圖11為中介軸承考慮潤滑和不考慮潤滑兩種工況下高壓轉子的時間歷程圖，可明顯看出中介軸承充分油霧潤滑的情況下，轉子振動幅值減小，振動幅值相對改變量為3.90%.圖12為與實驗相同工況下的仿真結果，考慮彈流潤滑作用后振動幅值減小3%.圖13對比了仿真和實驗條件下，轉速200、220、240、280、314 rad/s時，考慮彈流潤滑作用后高壓轉子振動幅值的相對改變量，在實驗轉速范圍內，轉子振幅相對改變量小于4%.低壓轉子和高壓轉子通過中介軸承耦合，低壓轉子有類似規律，此處不再贅述.可見實驗與仿真得到的轉子振幅相對改變量具有一致性，因此實驗結果可靠，進而能夠驗證仿真結果是合理的.

圖11 實驗結果

圖12 仿真結果

圖13 振幅變化百分數

由于實驗臺結構復雜，臨界轉速高等各種實驗條件的限制，以及目前對考慮潤滑的中介軸承-雙轉子系統實驗探究的文獻較少，研究還有待深入，因此本實驗中主要研究了考慮中介軸承彈流潤滑作用后雙轉子系統振動幅值的變化規律.

4 結 論

1)從幅頻曲線來看，彈流潤滑作用對一階共振峰附近高低壓轉子的振幅及共振峰位置影響較小，對高轉速區間的共振峰影響較大，使系統共振峰右移并且共振峰處振幅減小.低壓轉子和高壓轉子的響應規律一致.

2)分別改變中介軸承赫茲接觸剛度和徑向游隙，考慮彈流潤滑作用與不考慮彈流潤滑作用相比，一階共振峰處振幅改變小于5%，由于轉速較低時系統整體振幅較小，幅頻曲線無明顯變化.在二階共振峰處振幅改變較明顯，改變百分數在4%～9%之間.一階共振峰位置未發生偏移，二階共振峰向高頻移動2%～8%.改變潤滑油黏度，對低壓轉子和高壓轉子振動幅值影響小于1%.

3)實驗結果與仿真結果進行對比，在實驗轉速區間內，考慮中介軸承彈流潤滑作用時系統振動幅值相對改變量小于4%，仿真和實驗具有一致性.因此隨著加工誤差、工藝缺陷的降低以及數值計算精度的提高，為準確描述雙轉子系統的動力學特性，應考慮中介軸承彈流潤滑作用的影響.