銜接GMPE的城市燃氣管網連通易損性分析

宗成才，冀 昆，畢熙榮，任葉飛，張曉瑞，溫瑞智

(1.中國地震局工程力學研究所，哈爾濱 150080; 2.中國地震局地震工程與工程振動重點實驗室(中國地震局工程力學研究所)，哈爾濱 150080; 3.北京市煤氣熱力工程設計院有限公司，北京 100032)

隨著中國經濟發展和城市化進程的加快，準確真實評估城市燃氣管網不同地震動強度下的抗震性能變得尤為重要.根據研究尺度的不同，城市燃氣系統的易損性分析分為燃氣管線(微觀)和燃氣管網(宏觀)兩種，目前國內的研究多集中在前者[1]，即多局限于通過有限元分析等數值模擬手段對埋地管線、調壓站、儲氣罐等要素進行易損性分析；對城市燃氣管網整體的易損性分析關注較少，基于連通性的城市燃氣管網易損性可以定義為：城市燃氣管網在不同強度地震作用下，其連通性發生各種破壞狀態的發生概率.

基于圖論知識，燃氣管網的連通可靠性分析主要有解析算法和蒙特卡羅模擬法兩種：如李杰等[2]針對供燃氣管網系統提出了用于大型網絡抗震連通可靠度分析的遞推分解算法. 2012年,Poljan?ek等[3]假設燃氣管網各單元失效相互獨立，運用蒙特卡羅模擬的方法對燃氣管網進行了地震風險評估.基于蒙特卡羅模擬進行燃氣管網連通可靠性分析具有建模難度低，適用性強，以及收斂快速等多個優點，本文擬基于該分析思路來進行城市燃氣管網的連通易損性分析.此外地震動強度評估作為易損性分析的重要基礎環節是本文關注的另一個關鍵問題.目前國內大多采用GB18306-2015《中國地震動參數區劃圖》或GB 50032-2003《室外給水排水和燃氣熱力工程抗震設計規范》對城市的地震動參數進行宏觀估計[4]. 但是這種評估方式無法體現燃氣管網系統不同位置的地震動差異與不確定性. 2014年, Esposito等[5]在進行燃氣管網的地震風險評估時，提出了采用地面運動預測方程(GMPE)來評估意大利中部阿奎拉市的燃氣管網各位置的地震動強度. 本文借鑒該思路，嘗試將中國地震動預測方程(GMPE)應用到城市燃氣管網連通易損性分析中，同時將地震動預測方程中不確定性也通過隨機誤差變量抽樣來一并考慮.

綜上所述，為了綜合考慮地震動的區域分布差異性和地震動的不確定性，本文提出基于蒙特卡羅模擬的城市燃氣管網連通易損性分析方法.為驗證其適用性，以中國某城市燃氣管網作為實例進行了連通易損性分析，同時針對地震動預測方程中不確定性的影響進行重點對比研究.

1 城市燃氣管網連通易損性分析流程

城市燃氣管網系統由燃氣管線、燃氣門站、調壓站、用戶等部分組成，各功能單元相互連接構成網絡結構[6]. 將燃氣門站、調壓站、管線交匯處、用戶抽象為網絡節點，燃氣管線抽象為網絡的邊，其中燃氣門站記作網絡的源點，用戶端記作匯點便構成復雜網絡記為圖G，表示為G=(V,E),其中V為非空的節點集，E為不與V相交的邊集.圖G的節點和邊的連接關系可以表達為鄰接矩陣，記為A，稱A=A(G)=(aij)n×n為圖G的鄰接矩陣，n為節點數量，aij可表示為

(1)

對于拓撲網絡一般采用可達矩陣法進行連通性估計：即計算M=A+A2+A3+…+An-1,若Mij≠0,則表示i、j兩節點連通，反之，則i、j兩節點不連通[7].

下面首先介紹作為連通性計算依據的地震動強度指標估計方法，然后介紹燃氣管網中點、邊類單元的失效概率估計方法，最后給出基于蒙特卡羅模擬的燃氣管網連通易損性計算流程.

1.1 基于GMPE的燃氣管網地震動強度指標確定

由于城市燃氣管網系統其研究尺度一般在數百甚至上千平方公里，因此需要合理評估管網系統不同位置的地震動強度，并且需要考慮地震動自身的不確定性.如果以該地某一歷史地震或者目標活躍斷層的位置作為假想震源，則該城市燃氣管網各節點的地震動強度可以根據適用于該城市或區域的地震動預測方程進行評估計算.

本文采用了目前地震安全性評價工程中廣泛使用的文獻[8]地震動土層預測方程進行計算，長、短軸采用的預測方程模型為

lgY=C1+C2·M+C4·lg[R+C5·exp(C6·M)]+ε.

(2)

式中:Y為目標地震動強度指標(本文中為Pga和Pgv);M為面波震級;R為震中距;C1、C2、C4、C5、C6分別為回歸分析得到的參數;ε為體現不確定性的隨機誤差變量，呈均值為0，標準差為σlg(Y)的正態分布.

由圖1的某次地震動算例可知，地震動預測方程給出的其實是一定范圍的地震動強度指標預測區間，體現實際地震動觀測值的不確定性.對數強度指標預測值加減一倍對數標準差表征了16～84分位值的預測區間.

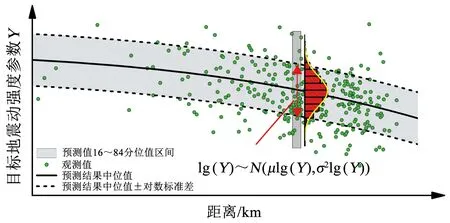
圖1 考慮地震動不確定性的地震動預測方程示意

1.2 節點與邊單元的失效概率估計方法

城市燃氣管網系統單元可以分為：1)點狀關鍵設施，如燃氣門站、調壓站、用戶端等；2)埋地燃氣管道.大量的震害調查研究表明[9]，相比于供水網絡等邊權網絡，以及供電網絡等點權網絡，城市燃氣管網系統震后應同時考慮點狀設施及管道失效的可能性.假定燃氣管網各單元之間失效相互獨立，某一部分單元在地震后失效，也會改變了整個管網的連通性.本文從節點和邊的角度分別給出兩類單元失效概率的估計方法.

1.2.1 節點失效概率

對于城市燃氣管網的點狀設施，本文僅考慮燃氣門站(源點)具有失效的可能性，而不考慮用戶端等其他節點的失效[10].作為主導燃氣門站失效的地震動參數Pga由上文的GMPE得到.本文中，燃氣門站的失效概率采用易損性曲線與故障樹分析相結合的方法.

不同功能設施的易損性曲線可以使用文獻[11]中的經驗統計模型，可表示為對數正態分布的函數，其可以轉換為標準正態分布進行計算，即

(3)

燃氣門站中影響地震后使用功能的重要設施可劃分為儲氣罐與計量調壓間，兩部分失效獨立，且失效狀態均設為嚴重破壞.本文采用文獻[12]中建議的儲氣罐與計量調壓間在嚴重破壞下的易損性函數參數值，見表1. 通過式(3)可以得到該源點地震作用強度達到Pga值時各子結構設施的失效概率，最后采用故障樹方法，計算出整個燃氣門站的失效概率(當考慮地震動預測方程中不確定性后，該失效概率為隨機變量)，即

P燃氣門站失效=1-(1-P計量減壓間失效)×(1-P儲氣罐失效).

(4)

表1 燃氣門站功能設施易損性函數參數值

1.2.2 邊失效概率

考慮影響埋地管線失效概率的地震動參數時，本文主要考慮Pgv[7]與Pgd[13-14](Permanent Ground Deformation,永久地面位移)的影響.

首先，由GMPE計算出各節點的Pgv后，邊(管線)的Pgv可以近似取所連兩節點的Pgv的平均值.

基于Pgv影響下管線平均震害率的經驗函數與管線的破裂沿管線遵循泊松分布的假設，同時考慮到城市燃氣管線較其他生命線系統最大的區別在于其不允許帶滲漏作業，采用兩態破壞準則，只有連通與失效兩種工作狀態，當埋地管線至少發生1處破壞時，管線失效.

本文采用文獻[12]中的震害率模型，表示為

Rf1=0.002 4×K1×Pgv.

(5)

式中：Rf1為埋地管線平均震害率，處/km；K1為與管材、接頭形式、場地土、管徑相關調整系數；Pgv為峰值地面速度. 其中

Pf1=1-P(0)=1-e-Rf1L.

(6)

式中：Pf1為Pgv影響下埋地管線震后失效概率(當考慮地震動預測方程中不確定性后，該失效概率為隨機變量)；L為計算管線的長度.

對于震后易發生永久地面位移地區管線以及一些因服役年限過長或腐蝕嚴重的管線，本文采用文獻[15]中的方法通過修正系數對Pgv影響下的燃氣管線失效概率進行修正，其失效概率Pf2為

Pf2=β1·β2·β3·β4·Pf1.

(7)

式中：β1為使用年限修正系數；β2為震陷修正系數；β3為液化修正系數；β4為腐蝕等其他因素修正系數.

1.3 基于蒙特卡羅模擬的燃氣管網地震連通易損性計算

首先定義燃氣管網的連通性評價指標.燃氣管網系統的連通性可以通過地震前后的接收燃氣用戶數量的比例來表示，并用CL(Connectivity loss)指標表示燃氣管網連通性的損失程度：

(8)

式中：npos為地震作用后，可以接收到燃氣的用戶數量；Npre為地震作用前，可以接收到燃氣的用戶數量.

破壞等級劃分方法見表2.

表2 城市燃氣管網基于CL值的破壞等級劃分

對于含有n個燃氣門站，m條埋地管線的燃氣管網模型，假設離散型隨機變量X=(X1,X2,…,Xn,Xn+1,…,Xn+m)表示燃氣管網震后狀態，x=(x1,x2,…,xn,xn+1,…,xn+m)表示X的一個樣本取值，xi表示第i個管網單元，有失效xi=0和不失效xi=1兩種狀態.CL(x)表示X=x時燃氣管網的CL值.

在某震級下，設定蒙特卡羅模擬次數N.若不考慮GMPE中不確定性ε，各節點的Pga、Pgv在每一次蒙特卡羅模擬中為定值(預測值)，但若考慮GMPE中地震動不確定性的影響，則用服從正態分布的隨機數模擬隨機誤差變量.每一次蒙特卡羅模擬中不同節點的Pga、Pgv不確定性是完全隨機的，同時因為地震動的不確定性，網絡中各單元的失效概率在每一次模擬中也均不相同.對所有單元產生服從0～1之間均勻分布的隨機數，當產生的隨機數小于該單元失效概率時，該單元失效，并生成新的受損網絡，形成新的鄰接矩陣，得到該次模擬下受損網絡的CL值.重復N次蒙特卡羅模擬，然后計算超過某CL值的次數與N的比值，得到該震級下，該城市燃氣管網的連通性指標CL的超越概率曲線.并求解N次模擬結果中CL值的均值和標準差即可得到CL的期望估計值與離散性.

連通損傷指標μ定義如下式所示，反映了燃氣管網在不同震級下連通性的平均損失程度，其值越大，表征燃氣管網的抗震能力越弱.

(9)

式中:N為蒙特卡羅模擬的次數;x(k)為第k次模擬抽樣得到的樣本值.

調整震級大小，重復上述步驟，得到不同震級下超過某破壞狀態的次數與N的比值，假設不同破壞狀態所對應的易損性曲線為對數分布函數，即可擬合得到城市燃氣管網連通性易損性曲線.

圖2 單元水平易損性——網絡水平易損性

圖3 城市燃氣管網連通易損性分析流程

2 城市燃氣管網連通易損性計算實例

本文選取中國華北某城市部分燃氣管網作為算例，采用上文的計算流程進行連通易損性分析，并對比討論了地震動預測方程中不確定性的影響.

2.1 燃氣管網拓撲建模

該市燃氣管道總長1 037.1 km，設計壓力分級為高壓A管線PN(公稱壓力)4.0 MPa，高壓B管線PN2.5 MPa，次高壓A管線PN1.6 MPa，對該市的燃氣管網進行拓撲網絡的構建，其中共9個燃氣門站，110個用戶，共306個節點，共326條邊.源點編號分別為：3、85、117、157、170、178、254、297、299.該市燃氣管網簡化圖如圖4所示.

圖4 該市燃氣管網簡化網絡圖

部分管段信息及節點編號見表3.

表3 燃氣管道屬性表

2.2 節點Pga、Pgv的確定

本文以該市歷史發生過破壞性地震的某個活斷層為假想震源所在斷層(如圖4所示)，長軸方向依據所在活動斷層走向確定.由于工程場地勘測鉆孔資料的缺失，本文暫不考慮燃氣管網所在地區的場地類型差異.通過聯立求解文獻[8]的長、短軸土層地震動預測方程得到震級5.0～8.0級(0.5級間隔)下管網各節點的Pga、Pgv值.取蒙特卡羅模擬次數N為10 000，其中5.0～8.0級地震發生時某一次模擬下的燃氣管網各節點Pga、Pgv與震中距的關系如圖5所示.從圖5中可以看出，在不考慮地震動不確定性時，各節點的地震動參數對數預測值在長短軸對數預測均值曲線之間；當引入隨機誤差變量時，模擬得到的各節點計算結果大致分布在長、短軸對數預測值加減一倍標準差的范圍.下文將對比討論是否考慮地震動不確定性對結果的影響.

圖5 不同震級下地震動參數考慮不確定性單次模擬結果與預測值對比

2.3 連通易損性指標計算

2.3.1 燃氣門站失效概率

基于GMPE確定各門站Pga后，采用表1中參數及式(3)、 (4)計算各源點的失效概率.

當考慮地震動不確定性時，由于同一點每一次模擬中的地震動強度指標分布情況都是不同的，導致不同模擬中得到的燃氣門站失效概率也各不相同.以7.0、8.0級地震為例，計算各源點考慮地震動不確定性后失效概率值的分布箱型圖如圖6所示.可以看到7.0級地震下，考慮地震動不確定性時各源點失效概率的均值均大于不考慮不確定性時的失效概率；造成該差異的原因是，由于地震動預測方程中地震動參數服從對數正態分布，所以在考慮GMPE中不確定性時抽樣得到的地震動參數樣本為偏態分布，其均值與地震動預測方程預測值(中位值)是不同的，這種差異也傳遞到了最后的計算結果中.在8.0級地震下，由于85，254，297，299節點(其空間分布如圖4所示)失效概率的中位值偏大，導致當Pga大于某值后其失效概率恒為1，故出現均值小于中位值的結果.

國內外均有學者在做燃氣管網連通可靠性分析時將燃氣管網系統作為邊權網絡系統，即僅考慮各邊失效的可能性[16].由圖6中各燃氣門站失效概率分布可知，某些門站失效概率均值也很大.因此無論在進行燃氣管網的可靠性，還是易損性分析時，燃氣門站的失效概率不可忽略.

圖6 7.0、8.0級地震下各燃氣門站失效概率

2.3.2 埋地管線失效概率

計算埋地管線的失效概率時，式(5)中K1依據文獻[12]，綜合考慮管材、接頭形式、場地土、管徑等因素分別取0.60與0.15.依據文獻[15]，建設于2015—2019年的管線β1=1.0，建設于2010—2014年的管線β1=1.1，建設于2010年之前的管線β1=1.2；由該市的地質資料可知，該市A、B區是震陷高發區，故在小于7.0級地震發生時，A、B區的埋地管線在計算失效概率時，修正系數β2=1.2，當發生大于等于7.0級地震時，修正系數β2=1.5；各管線的β3、β4均取值為1.各管線在7.0、8.0級地震發生時，按考慮地震動不確定性時各管線失效概率均值由小到大排列，并與相同管線在不考慮不確定性時的失效概率值相比較，結果如圖7(a)所示.可以看出由于受到Pgv服從對數正態分布影響，在考慮不確定性時各管線的失效概率均值均大于未考慮不確定性時各管線的失效概率.

2.3.3 連通損傷指標計算

不同震級下連通損傷指標結果如圖7(b)所示，由表2中的破壞等級劃分可知，考慮地震動不確定性時，在發生7.0級地震后，該市的燃氣管網的連通性能發生輕微破壞，發生8.0級地震時燃氣管網的連通性能發生中等破壞.由上述分析可見，本文提出的連通損傷指標可以通過具體數值刻畫某市燃氣管網在不同震級下連通性的損失程度，可以作為衡量燃氣管網的魯棒性的指標之一，指導管網建設決策，同時為接下來城市燃氣管網可恢復性的研究做鋪墊，具有較好的工程應用價值.

圖7 燃氣管線失效概率和不同震級下連通損傷指標

2.4 燃氣管網連通易損性曲線

不同震級下，該城市燃氣管網的連通性指標CL的超越概率曲線及不同破壞狀態的易損性曲線如圖8所示.不同破壞狀態下震級均值與標準差見表4.

圖8 城市燃氣管網連通易損性計算結果

表4 不同破壞狀態下震級均值與標準差

由該計算結果可知，考慮地震動不確定性時，在發生5.0、5.5、6.0級地震后，該市燃氣管網連通性能完好的概率為56%、38%、6%. 各震級下，考慮地震動預測方程中不確定性后的該市燃氣管網的連通損失超越概率均大于不考慮不確定性時的數值，易損性曲線也反映了在考慮不確定性時，該市燃氣管網在不同震級下連通性能超過某破壞狀態的概率均偏大.原因在于在考慮某一震級下各地地震動參數的不確定性時，其地震動參數為偏態分布，均值大于中位值，故導致燃氣管網中單元的失效概率均值增大，導致整個管網的連通性更易損壞.

3 結 論

1)基于地震動預測方程(GMPE)確定燃氣管網各位置的地震動強度指標，然后確定燃氣管網點狀設施、邊單元(埋地管道)的失效概率.最后通過蒙特卡羅模擬，統計震后的管網中未通氣的節點數量確定反映系統連通性能損失的指標，最后在多個震級下重復該過程，可以得到燃氣管網的整體連通易損性曲線.

2)算例城市在不同震級下的連通損傷指標結果表明，在目標斷層位置發生7.0級地震后，該市的燃氣管網的連通性能發生輕微破壞，發生8.0級地震時燃氣管網的連通性能發生中等破壞.在發生5.0級、5.5級、6.0級地震后，該市燃氣管網連通性能完好的概率為56%、38%、6%.

3)地震動的不確定性對連通性指標CL的超越概率曲線及不同破壞狀態的易損性曲線計算結果影響較大.考慮地震動預測方程中不確定性后，該市燃氣管網的連通損失超越概率均大于忽視不確定性時的數值，后者可能會低估實際地震下管網連通性能的損失.